代码随想录训练营day14
101. 对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
func isSymmetric(root *TreeNode) bool {if root == nil{ return true}return judge(root.Left,root.Right)
}func judge(lf *TreeNode , ri *TreeNode)bool{if lf == nil && ri ==nil{ return true}if lf == nil || ri ==nil{ return false}if lf.Val != ri.Val{return false}return judge(lf.Left,ri.Right) && judge(lf.Right,ri.Left)
}102. 二叉树的层序遍历
var arr [][]int
func levelOrder(root *TreeNode) [][]int {arr= [][]int{}depth:=0order(root,depth)return arr
}func order(root *TreeNode,depth int){if root ==nil{return }if len(arr) == depth{arr = append(arr,[]int{})} //这个地方是因为要追加一个新的数组来保存该层的节点元素arr[depth] = append(arr[depth],root.Val)order(root.Left,depth+1)order(root.Right,depth+1)}
226. 翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
func invertTree(root *TreeNode) *TreeNode {if root == nil { return nil }root.Left ,root.Right = root.Right,root.LeftinvertTree(root.Left)invertTree(root.Right)return root
}相关文章:

代码随想录训练营day14
101. 对称二叉树 给你一个二叉树的根节点 root , 检查它是否轴对称。 func isSymmetric(root *TreeNode) bool {if root nil{ return true}return judge(root.Left,root.Right) }func judge(lf *TreeNode , ri *TreeNode)bool{if lf nil && ri nil{ retu…...

功能测试进阶自动化测试如何摸清学习方向,少走弯路呢?
目录 抛开疑问,只做学术探讨 小白在想什么? 盖楼之前先打好地基,首先需要学习一门语言 语言入门后,正式踏上开始自动化成神之路,入门篇Selenium 玩腻了Selenium 开始接触自动化框架unittest/testNG 不满足于单元…...

检测前端是否可以ping通后端返回的ip地址
检测前端是否可以ping通后端返回的ip地址 前端检测是否可ping通ip地址(PC端)前端检测是否可ping通ip地址(uniapp小程序端) 前端检测是否可ping通ip地址(PC端) // 前端检测是否可ping通ip地址 ping…...

SMART司马他法则(目标管理)
S代表具体(Specific),指绩效考核要切中特定的工作指标,不能笼统; M代表可度量(Measurable),指绩效指标是数量化或者行为化的,验证这些绩效指标的数据或者信息是可以获得的; A代表可实现(Attainable)&…...
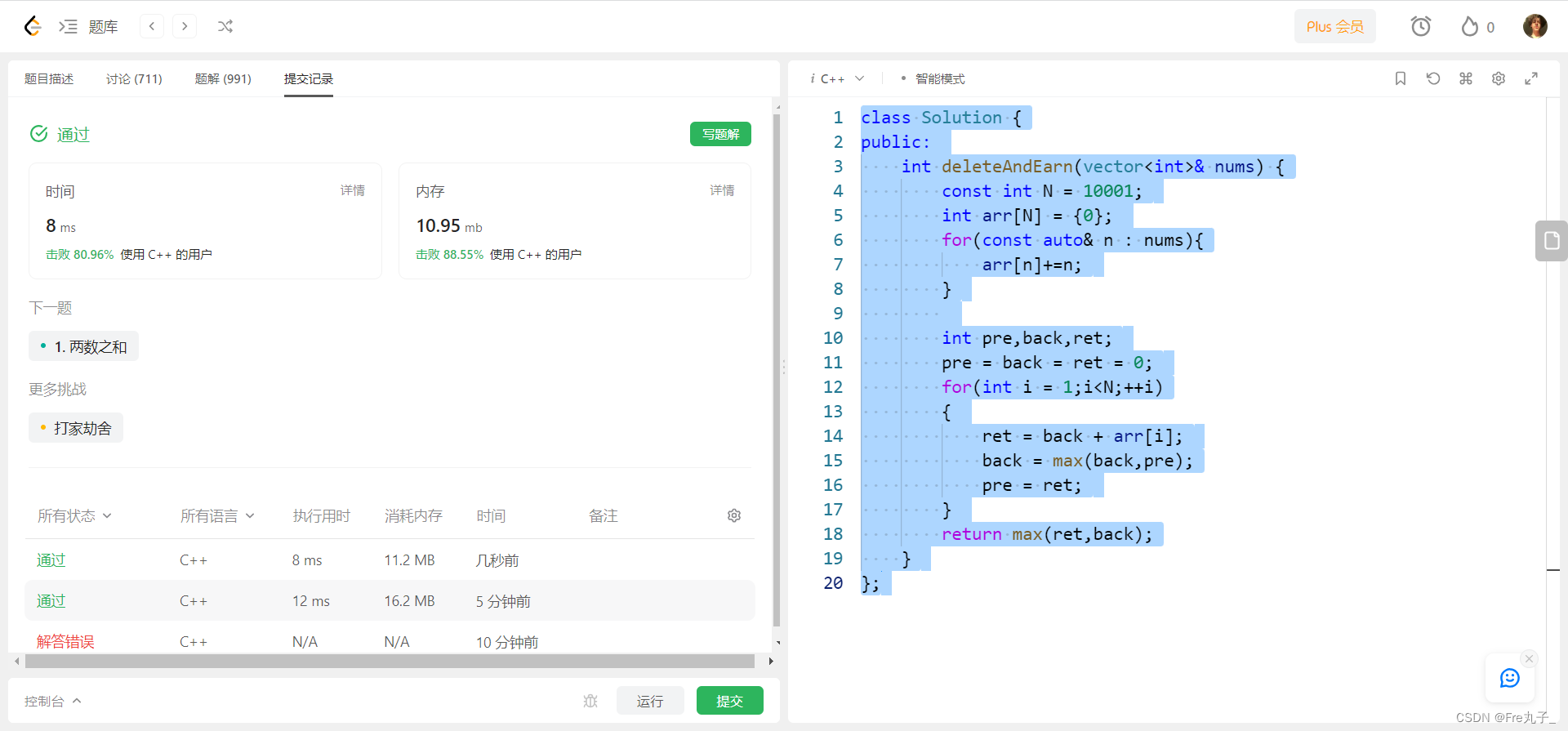
【LeetCode】删除并获得点数
删除并获得点数 题目描述算法分析编程代码空间优化 链接: 删除并获得点数 题目描述 算法分析 编程代码 class Solution { public:int deleteAndEarn(vector<int>& nums) {const int N 10001;int arr[N] {0};for(const auto& n : nums){arr[n]n;}vector<in…...

SciencePub学术 | 传感器类重点SCIE征稿中
SciencePub学术 刊源推荐: 传感器类重点SCIE征稿中!信息如下,录满为止: 一、期刊概况: 传感器类重点SCIE 【期刊简介】IF:2.0-2.5,JCR3区,中科院4区; 【版面类型】正刊࿱…...

移动端开发基础总结
移动端学习总结 (适合于复习) 移动端基础 技术选型: 单独制作移动端页面(主流) 流式布局(百分比布局)flex弹性布局(强烈推荐)lessrem媒体查询布局混合布局 响应式页面兼容移动端(…...
)
小X学游泳(深搜)
第一题 题目描述 小X想要学游泳。 这天,小X来到了游泳池,发现游泳池可以用N行M列的格子来表示,每个格子的面积都是1,且格子内水深相同。 由于小X刚刚入门,他只能在水深相同的地方游泳。为此,他把整个游泳池…...

分布式协议与算法——拜占庭将军问题
拜占庭将军问题 背景:以战国时期为背景 战国时期,齐、楚、燕、韩、赵、魏、秦七雄并立,后来秦国的势力不断强大起来,成了东方六国的共同威胁。于是,这六个国家决定联合,全力抗秦,免得被秦国各个…...

MySQL数据库管理的基本原则和技巧
MySQL数据库是一种常用的关系型数据库管理系统,用于存储和管理大量的数据。在进行MySQL数据库管理时,有一些基本原则和技巧可以帮助我们更有效地管理数据库。 数据库设计原则: 合理规划数据表结构: 根据数据之间的关系和业务需求…...
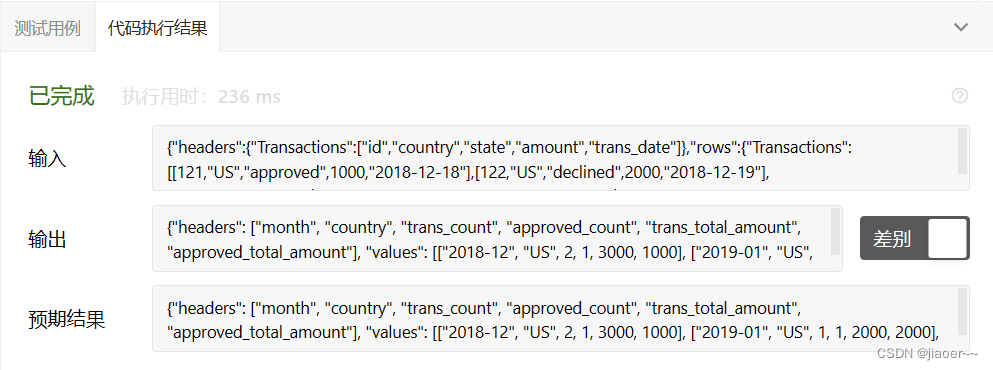
SQL-每日一题【1193. 每月交易 I】
题目 Table: Transactions 编写一个 sql 查询来查找每个月和每个国家/地区的事务数及其总金额、已批准的事务数及其总金额。 以 任意顺序 返回结果表。 查询结果格式如下所示。 示例 1: 解题思路 1.题目要求我们查找每个月和每个国家/地区的事务数及其总金额、已批准的事务数…...

探析青少年口才训练在个人发展中的重要性与影响
论文题目:探析青少年口才训练在个人发展中的重要性与影响 摘要: 本论文旨在探讨青少年口才训练对个人发展的重要性和影响。通过对相关文献的综述和实证研究的分析,论文将阐述口才训练对青少年自信心、表达能力和思维能力的提升,以…...

HTML 元素的 class 和 id 属性有何区别?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 唯一性⭐ 选择器权重⭐ JS操作⭐ CSS和JavaScript引用⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏…...

关于GKPhoto点击放大没有图片只有缺省图
GKPhoto,点进去看看,人家可传递的不止有url,还有UiImage NSString *photo self.detailModel.teacherModel.teacher_picture; NSString *placeHoldStr "ing_morentouxiang"; NSMutableArray *photos [NSMutableArray new]; GKPhoto *phot…...
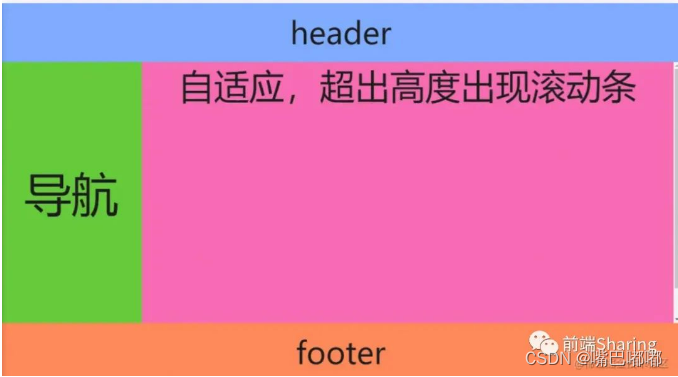
建议收藏!总结了 42 种前端常用布局方案
对 CSS 布局掌握程度决定你在Web开发中的开发页面速度。随着Web技术的不断革新,实现各种布局的方式已经多得数不胜数了。 本篇文章总结了四十二种CSS的常见布局,这四十二种布局可以细分为如下几类: 水平居中垂直居中水平垂直居中两列布局三…...

spring AOP两种动态代理
本文开始 1.什么是动态代理? 动态代理:本来是通过直接访问目标对象的,但是找个代理对象替你进行访问目标对象,这就是动态代理过程; 例如:买饭作为目标对象,自己不想亲自跑腿,就点个…...

英语——副词
副词是指在句子中表示行为或状态特征的词,常用来修饰动词、形容词、其他副词或者句子等,表示时间、地点、方式和程度等,在句子中作状语。 第一节 副词的基本形式 一、副词的构成 1.许多副词都是由形容词变化而来。 (1)大部分副词由相应形容词直接加-ly构成。quick→q…...
Vue 本地应用 记事本 v-on v-model v-for使用
新增功能 vue当中如何生成列表结构?使用的指令是v-for,同时要有一个可以生成列表的数据,常用的是数组。记事本里面的内容并不复杂,所以这里使用字符串数组就行了。 获取用户输入的内容使用绑定v-model,双向数据绑定&a…...

智能质检技术的核心环节:语音识别和自然语言处理
随着呼叫中心行业的快速发展和客户服务需求的不断提高,越来越多的企业开始采用智能质检技术,以提高呼叫中心的质量和效率。而在智能质检技术中,语音识别和自然语言处理是其核心环节,对于提高质检的准确性和效率具有重要作用。 语音…...

Python 中的值传递 和 引用传递
在 Python 当中的函数调用当中, numpy 和 torch.tensor 都 是按照 引用传递 传到函数里面的,也就是说 修改 传入函数的 形参,也会导致 未传入之前的形参 发生 变化。 position 是一个 tensor; 下面这段代码第一行,如果在函数里面…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
