分布式协议与算法——拜占庭将军问题
拜占庭将军问题
背景:以战国时期为背景
战国时期,齐、楚、燕、韩、赵、魏、秦七雄并立,后来秦国的势力不断强大起来,成了东方六国的共同威胁。于是,这六个国家决定联合,全力抗秦,免得被秦国各个击破。一天,苏秦作为合纵长,挂六国相印,带着六国的军队叩关函谷,驻军在了秦国边境,为围攻秦国作准备。但是,因为各国军队分别驻扎在秦国边境的不同地方,所以军队之间只能通过信使互相联系,这时,苏秦面临了一个很严峻的问题:如何统一大家的作战计划?
万一一些诸侯国在暗通秦国,发送误导性的作战信息,怎么办?如果信使被敌人截杀,甚至被敌人间谍替换,又该怎么办?这些都会导致自己的作战计划被扰乱,然后出现有的诸侯国在进攻,有的诸侯国在撤退的情况,而这时,秦国一定会趁机出兵,把他们逐一击破的。
问题:二忠一叛的难题
现有三个国家攻打秦国,分别叫齐、楚、燕。同时,又因为秦国很强大,所以只有半数以上的将军参与进攻,才能击败敌人。此时,将军们需要通过信使传递消息,然后协商一致之后,才能在同一时间发动进攻。
正常的情况:
例如:
- 齐根据侦查情况决定撤退。
- 楚和燕根据侦查信息,决定进攻。
这样最终进攻和撤退的二者的占比为2:1,因此最终会执行进攻的命令。
不正常的情况,存在叛军(恶意节点):
假设齐和燕为忠诚将军,楚为叛将。现在齐决定撤退、燕决定进攻。而由于楚已经叛变,他向齐传达“撤退”的命令,向燕传达“进攻”的命令。因此齐看到的结果为:进攻:撤退 = 1:2;燕看到的结果为:进攻:撤退 = 2:1。最终就燕自己去进攻秦军了,被灭了。
解决方法一:口信消息型拜占庭问题之解
三位将军分拨一部分军队,由苏秦带领。这样3位将军的作战讨论,变成了4位将军的作战讨论,这样可以增加讨论中忠诚将军的数量。
然后,四位将军约定了,如果没有收到命令,就执行预设的默认命令,例如撤退。需要进行多轮作战信息协商(协商的轮次与叛将的数量有关):
第一轮:
- 先发送作战信息的将军作为指挥官,其他的将军作为副官;
- 指挥官将他的作战信息发送给每位副官;
- 每位副官,将从指挥官处收到的作战信息,作为他的作战指令;如果没有收到作战信息,将把默认的“撤退”作为作战指令。
第二轮:
- 除了第一轮的指挥官外,剩余的 3 位将军将分别作为指挥官,向另外 2 位将军发送作战信息;
- 然后,这 3 位将军按照“少数服从多数”,执行收到的作战指令。
如果这里需要协商多轮,那么除了前面几轮的指挥官外,剩余的将军作为指挥官将作战信息发送每位副官。
具体协商过程:
分别以忠诚将军和叛将先发送作战信息为例:
1、忠诚将军先发送作战信息:
假设忠将苏秦先发送作战信息,作战指令是“进攻”。那么在第一轮作战协商中,苏秦向齐、楚、燕发送作战指令“进攻”,意味着齐、楚、燕分别收到了“进攻”的信息,并作为自己的作战指令。

在第二轮作战信息协商中,齐、楚、燕分别作为指挥官,分别向另外两位(第一轮指挥官苏秦除外)发送作战信息“进攻”。由于楚已经叛变,他为了干扰作战计划,向另外两位将军发送了“撤退”作战命令。

最终,齐和燕收到的作战信息都是“进攻、进攻、撤退”。按照少数服从多数的原则,执行“进攻”指令,实现了作战计划的一致性。
2、叛将先发送作战信息:
当叛将先发送作战消息,干扰作战计划时。在第一轮协商中,楚向苏秦发送“进攻作战指令”,向齐、燕发送“撤退”作战指令。苏秦、齐、燕收到后并将其作为自己的作战指令。

在第二轮作战信息协商中,苏秦、齐、燕分别作为指挥官,向另外两位发送作战信息。

最终苏秦、齐、燕收到的信息都是“撤退、撤退、进攻”,按照少数服从多数的原则,执行“撤退”指令,实现了作战计划的一致性。
这个算法的前提:
- 如果叛将人数为m,将军人数不能少于3m+1(也就是:n位将军,最多能容忍(n-1)/3 位叛将)。
- 叛将数m决定递归循环的次数(进行多少轮作战信息协商),即m+1轮。
二忠一叛问题中,在存在1位叛将的情况下,必须增加1位将军。那么有没有办法在不增加将军人数的时候,直接解决二忠一叛的难题?可以通过签名消息型拜占庭问题之解进行解决。
解决办法二:签名消息型拜占庭问题之解
还可以通过签名的方式,在不增加将军人数的情况下,解决二忠一叛的难题。签名具有如下的特性:
- 忠诚将军的签名无法伪造,而且对他签名消息的内容进行任何更改都会被发现;
- 任何人都能验证将军签名的真伪。
与口信消息型拜占庭问题之解类似,签名消息型拜占庭问题之解同样需要多轮协商。协商的过程也与口信消息型拜占庭问题之解类似,但最终执行作战计划时并不是使用少数服从多数的原则。下面同样以忠诚将军和叛将分别先发送消息为例。
忠诚将军先发送消息
第一轮协商中,忠诚将军齐分别向楚和燕发送“进攻”的作战信息,燕和楚收到进攻的作战信息后将其作为自己的作战消息。

第二轮协商中,楚和燕分别作为指挥官分别向另一位将军(第一轮将军除外)发送作战信息。叛将楚修改或伪造作战信息,将“撤退”信息发送给了燕。那么燕在收到楚的作战信息的时候,会发现齐的作战信息被修改,楚已经叛变,这是燕会忽视来自楚的作战信息,最终执行齐发送的作战信息。

叛将先发送消息
第一轮协商中,叛将楚向齐发送“撤退”的作战消息,向燕发送“进攻”的作战消息。

第二轮协商中,燕和齐分别作为指挥官分别向另一位将军(第一轮将军除外)发送作战信息。此时齐收到了[撤退、进攻]两个作战消息,燕收到了[进攻、撤退]两个作战消息。但是齐和燕会按照一定的规则在排序后的所有已接受的指令中选取一个(例如按照排序规则后的作战顺序为[进攻,撤退],都选择第一个作战计划)作战计划进行执行。最终执行一致的作战计划。
齐、燕收到的信息列表是内容是一样的,只是顺序不一样,使用相同的排序算法,选取策略,可以保证选取的指令时一样的

这个算法的前提是:
1、n位将军,最多允许 (n-2)位叛将。
2、同样需要多轮协商,如果叛将数位m,那么需要m + 1轮协商。
那如何实现签名消息呢?
可以使用非对称加密算法(如RSA),发送方使用哈希算法(如MD5)进行摘要,然后使用私钥对摘要进行加密,生成数字签名。然后将加密摘要和消息一起发送给接受方。接受方收到消息和加密摘要后,会用公钥对加密摘要进行解密,并对消息内容进行摘要,将两个摘要进行对比,以判断消息是否被篡改。
私钥加密,公钥解密。可以保证消息不会被冒充,因为私钥是不可泄漏的。如果公钥能正常解密出私钥加密的内容,就能证明这个消息是来源于持有私钥身份的人发送的。
感觉使用签名消息型拜占庭问题之解会更消耗算力一点。
小结
将将军作战中的场景与计算机世界的分布式场景进行对应:
- 故事里的将军,可以理解为计算机节点。
- 忠诚将军,可以理解为正常运行的计算机节点。
- 叛变将军,可以理解为出现故障并会发送误导信息的计算机节点。
- 信使被杀,可以理解为通讯故障、信息丢失。
- 信使被间谍替换,可以理解为通讯被中间人攻击,攻击者在恶意伪造信息和劫持通讯。
拜占庭将军问描述的是最困难的,也是最复杂的一种分布式故障场景,除了存在故障行为,还存在恶意行为的场景。因此在存在恶意行为的场景中(如数字货币的区块链技术中),必须使用拜占庭容错算法(Byzantine Fault Tolerance,BFT)。除了上面提到的两种算法(口信消息型拜占庭问题之解、签名消息型拜占庭问题之解),常用的拜占庭容错算法还有:PBFT算法,PoW算法。
在计算机分布式系统中,最常用的是非拜占庭容错算法,即故障容错算法(Crash Fault Tolerance,CFT)。CFT 解决的是分布式的系统中存在故障,但不存在恶意节点的场景下的共识问题。 也就是说,这个场景可能会丢失消息,或者有消息重复,但不存在错误消息,或者伪造消息的情况。常见的算法有 Paxos 算法、Raft 算法、ZAB 协议。
参考
- 分布式协议与算法实战 学习笔记
相关文章:

分布式协议与算法——拜占庭将军问题
拜占庭将军问题 背景:以战国时期为背景 战国时期,齐、楚、燕、韩、赵、魏、秦七雄并立,后来秦国的势力不断强大起来,成了东方六国的共同威胁。于是,这六个国家决定联合,全力抗秦,免得被秦国各个…...

MySQL数据库管理的基本原则和技巧
MySQL数据库是一种常用的关系型数据库管理系统,用于存储和管理大量的数据。在进行MySQL数据库管理时,有一些基本原则和技巧可以帮助我们更有效地管理数据库。 数据库设计原则: 合理规划数据表结构: 根据数据之间的关系和业务需求…...
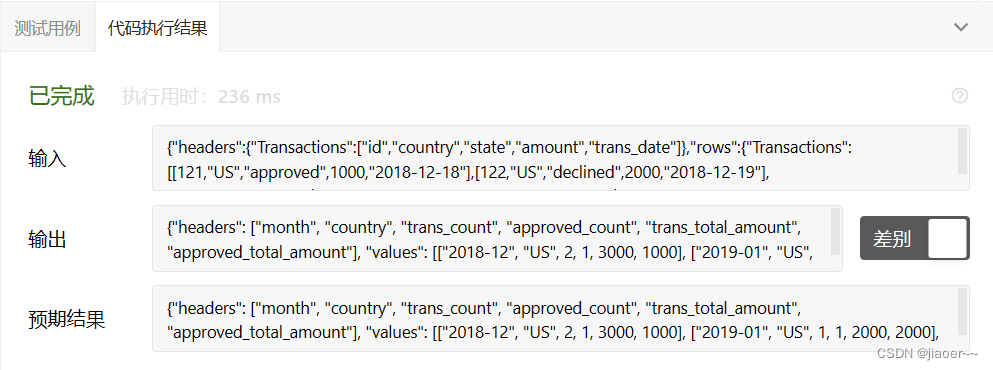
SQL-每日一题【1193. 每月交易 I】
题目 Table: Transactions 编写一个 sql 查询来查找每个月和每个国家/地区的事务数及其总金额、已批准的事务数及其总金额。 以 任意顺序 返回结果表。 查询结果格式如下所示。 示例 1: 解题思路 1.题目要求我们查找每个月和每个国家/地区的事务数及其总金额、已批准的事务数…...

探析青少年口才训练在个人发展中的重要性与影响
论文题目:探析青少年口才训练在个人发展中的重要性与影响 摘要: 本论文旨在探讨青少年口才训练对个人发展的重要性和影响。通过对相关文献的综述和实证研究的分析,论文将阐述口才训练对青少年自信心、表达能力和思维能力的提升,以…...

HTML 元素的 class 和 id 属性有何区别?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 唯一性⭐ 选择器权重⭐ JS操作⭐ CSS和JavaScript引用⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏…...

关于GKPhoto点击放大没有图片只有缺省图
GKPhoto,点进去看看,人家可传递的不止有url,还有UiImage NSString *photo self.detailModel.teacherModel.teacher_picture; NSString *placeHoldStr "ing_morentouxiang"; NSMutableArray *photos [NSMutableArray new]; GKPhoto *phot…...
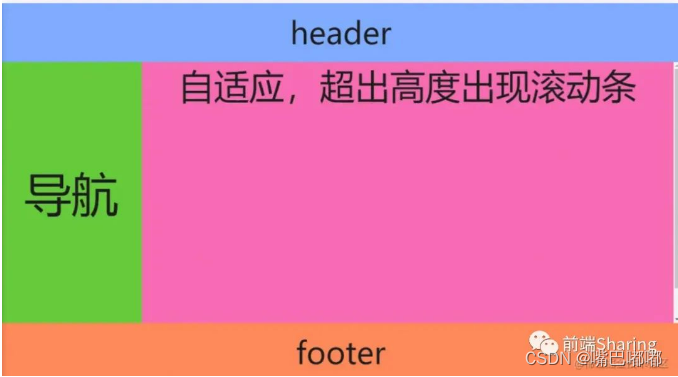
建议收藏!总结了 42 种前端常用布局方案
对 CSS 布局掌握程度决定你在Web开发中的开发页面速度。随着Web技术的不断革新,实现各种布局的方式已经多得数不胜数了。 本篇文章总结了四十二种CSS的常见布局,这四十二种布局可以细分为如下几类: 水平居中垂直居中水平垂直居中两列布局三…...

spring AOP两种动态代理
本文开始 1.什么是动态代理? 动态代理:本来是通过直接访问目标对象的,但是找个代理对象替你进行访问目标对象,这就是动态代理过程; 例如:买饭作为目标对象,自己不想亲自跑腿,就点个…...

英语——副词
副词是指在句子中表示行为或状态特征的词,常用来修饰动词、形容词、其他副词或者句子等,表示时间、地点、方式和程度等,在句子中作状语。 第一节 副词的基本形式 一、副词的构成 1.许多副词都是由形容词变化而来。 (1)大部分副词由相应形容词直接加-ly构成。quick→q…...
Vue 本地应用 记事本 v-on v-model v-for使用
新增功能 vue当中如何生成列表结构?使用的指令是v-for,同时要有一个可以生成列表的数据,常用的是数组。记事本里面的内容并不复杂,所以这里使用字符串数组就行了。 获取用户输入的内容使用绑定v-model,双向数据绑定&a…...

智能质检技术的核心环节:语音识别和自然语言处理
随着呼叫中心行业的快速发展和客户服务需求的不断提高,越来越多的企业开始采用智能质检技术,以提高呼叫中心的质量和效率。而在智能质检技术中,语音识别和自然语言处理是其核心环节,对于提高质检的准确性和效率具有重要作用。 语音…...

Python 中的值传递 和 引用传递
在 Python 当中的函数调用当中, numpy 和 torch.tensor 都 是按照 引用传递 传到函数里面的,也就是说 修改 传入函数的 形参,也会导致 未传入之前的形参 发生 变化。 position 是一个 tensor; 下面这段代码第一行,如果在函数里面…...

【雕爷学编程】Arduino动手做(200)---WS2812B幻彩LED灯带6
37款传感器与模块的提法,在网络上广泛流传,其实Arduino能够兼容的传感器模块肯定是不止37种的。鉴于本人手头积累了一些传感器和执行器模块,依照实践出真知(一定要动手做)的理念,以学习和交流为目的&#x…...

ChatGPT在工作中的七种用途
1. 用 ChatGPT 替代谷歌搜索引擎 工作时,你一天会访问几次搜索引擎?有了 ChatGPT,使用搜索引擎的频率可能大大下降。 据报道,谷歌这样的搜索引擎巨头,实际上很担心用户最终会把自己的搜索工具换成 ChatGPT。该公司针对…...

redis 持久化 与 键淘汰策略
redis运维核心: aof日志(全持久化 增量) 、 rdb(半持久化/全量备份) 、 键淘汰策略 、 高可用 1、Redis是基于内存的,一旦Redis重启/退出/故障,内存的数据将会全部丢失。故而有了持久化。 2、持久化:将内存中的数据存于磁盘中&am…...
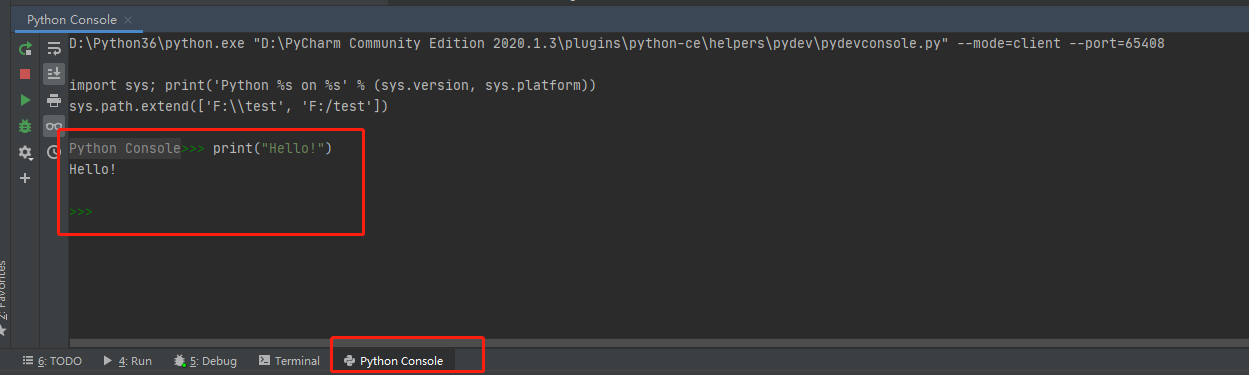
PyCharm新手入门指南
安装好Pycharm后,就可以开始编写第一个函数:Hello World啦~我们就先来学习一些基本的操作,主要包含新建Python文件,运行代码,查看结果等等。 文章主要包含五个部分: 一、界面介绍 主要分为菜单栏、项目目录…...
【图像去噪】基于混合自适应(EM 自适应)实现自适应图像去噪研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
[保研/考研机试] KY102 计算表达式 上海交通大学复试上机题 C++实现
描述 对于一个不存在括号的表达式进行计算 输入描述: 存在多组数据,每组数据一行,表达式不存在空格 输出描述: 输出结果 示例1 输入: 6/233*4输出: 18思路: ①设立运算符和运算数两个…...

源码解析Collections.sort ——从一个逃过单测的 bug 说起
本文从一个小明写的bug 开始,讲bug的发现、排查定位,并由此展开对涉及的算法进行图解分析和源码分析。 事情挺曲折的,因为小明的代码是有单测的,让小明更加笃定自己写的没问题。所以在排查的时候,也经历了前世的500年…...

一周 AIGC 丨苹果下架多款 AIGC 应用,阿里云开源通义千问 70 亿参数模型
多个 AIGC 应用在苹果应用商店下架,包含数据采集和使用不够规范等问题。阿里云开源通义千问 70 亿参数模型,包括通用模型 Qwen-7 B 和对话模型 Qwen-7 B-Chat。腾讯混元大模型开始应用内测,内部多个业务线接入测试。百度智能云“千帆大模型平…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

【多线程初阶】单例模式 指令重排序问题
文章目录 1.单例模式1)饿汉模式2)懒汉模式①.单线程版本②.多线程版本 2.分析单例模式里的线程安全问题1)饿汉模式2)懒汉模式懒汉模式是如何出现线程安全问题的 3.解决问题进一步优化加锁导致的执行效率优化预防内存可见性问题 4.解决指令重排序问题 1.单例模式 单例模式确保某…...

前端打包工具简单介绍
前端打包工具简单介绍 一、Webpack 架构与插件机制 1. Webpack 架构核心组成 Entry(入口) 指定应用的起点文件,比如 src/index.js。 Module(模块) Webpack 把项目当作模块图,模块可以是 JS、CSS、图片等…...
