2023河南萌新联赛第(五)场:郑州轻工业大学 --Kruskal
题目描述
给定一张nnn个点的无向完全图,其中两点之间的路径边权为两点编号的按位与(编号为 (1,2,...,n)(1,2,...,n)(1,2,...,n)),即w(u,v)=u&v(1≤u,v≤n)w\left(u, v \right )=u\&v \left( 1 \le u, v \le n \right)w(u,v)=u&v(1≤u,v≤n),求该图最小生成树的边权和。
输入描述:
本题包含多组数据
第一行包含一个正整数T(1≤T≤2×105)T \left( 1 \le T \le 2 \times 10^5 \right)T(1≤T≤2×105),代表测试用例的组数。
对于每组数据:
第一行输入一个正整数n(2≤n<109)n \left( 2 \le n < 10^{9} \right)n(2≤n<109),代表该完全图的节点个数。
输出描述:
对于每组数据: 输出一行一个整数,代表该完全图最小生成树的边权和。
示例1
输入
1
3输出
1
说明
对于n=3n=3n=3的完全图,生成树的方式有如下三种:
*
,生成树的权值之和为0+1=1
*
,生成树的权值之和为1+2=3
*
,生成树的权值之和为0+2=2
选择第一种连接方式最优,因此最小生成树的权值之和为1。
思路:
做这个题首先要先了解二进制的一些小特征
第一个,我们要知道所有的偶数二进制的最后以为一定是0,所以我可以用 1 去连接所有的偶数,总权值和为0
第二个,我们要知道一个特点,就是二进制的中,高位的一个1,即使后面全是0,他也比高位为0后面全是1的数大,所以我们的奇数就可以分为两类了,一类是二进制全部为1的,一类是二进制中有0存在的。
二进制中全部为1的数,我们要想让他贡献最小,可以考虑他的下一个数存不存在。比如 就可以用
来连接,他的贡献也是 0.
二进制中有 0 存在的,我们就可以找小于他的一个数来跟他连接,找的这个数的二进制各位数字恰好与其相反,所以这一类的贡献也都是0
综上,我们就可以看出答案只有两种情况,一个是1,一个是0。总结起来,其实就是看最后一个数属于哪一类,如果属于二进制中全1的一类的话,他的下一个就不存在了,所以我们只能考虑让他跟1连,与运算之后是1.(与其他数运算结果为什么大,就是第二条)
AC代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5+10;
int a[N];
void solve(){int n;cin >> n;if(n % 2 == 0){cout << "0\n";}else{bool flag = 0;while(n){if(n % 2 == 0){flag = 1;break;}n /= 2;}if(flag)cout << "0\n";else cout << "1\n";}
}
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int T = 1;cin >> T;while(T--){solve();}return 0;
}相关文章:
2023河南萌新联赛第(五)场:郑州轻工业大学 --Kruskal
题目描述 给定一张nnn个点的无向完全图,其中两点之间的路径边权为两点编号的按位与(编号为 (1,2,...,n)(1,2,...,n)(1,2,...,n)),即w(u,v)u&v(1≤u,v≤n)w\left(u, v \right )u\&v \left( 1 \le u, v \le n \right)w(u,v…...
Maven引入本地jar包
maven做为一种强大的依赖管理工具,可以帮助我们更方便的管理项目中的依赖;而在使用过程中我们难免会有需要引入本地jar包的需求,这里踩过坑之后我分享俩种引入方式; 1.上传jar到本地maven仓库,再引入 使用此方法后可…...

Java并发编程实战——结构化并发应用程序
文章目录 6 任务执行6.1 在线程中执行任务6.1.1 串行地执行任务6.1.2 显式地为任务创建线程6.1.3 无限制创建线程的不足 6.2 Executor框架6.2.1 示例:基于Executor的Web服务器6.2.2 执行策略6.2.3 线程池6.2.4 Executor的生命周期6.2.5 延迟任务与周期任务 6.3 找出…...
uniapp echarts 点击失效
这个问题网上搜了一堆,有的让你降版本,有的让你改源码。。。都不太符合预期,目前我的方法可以用最新的echarts。 这个方法就是由npm安装转为CDN,当然你可能会质疑用CDN这样会不稳定,那如果CDN的地址是本地呢࿱…...
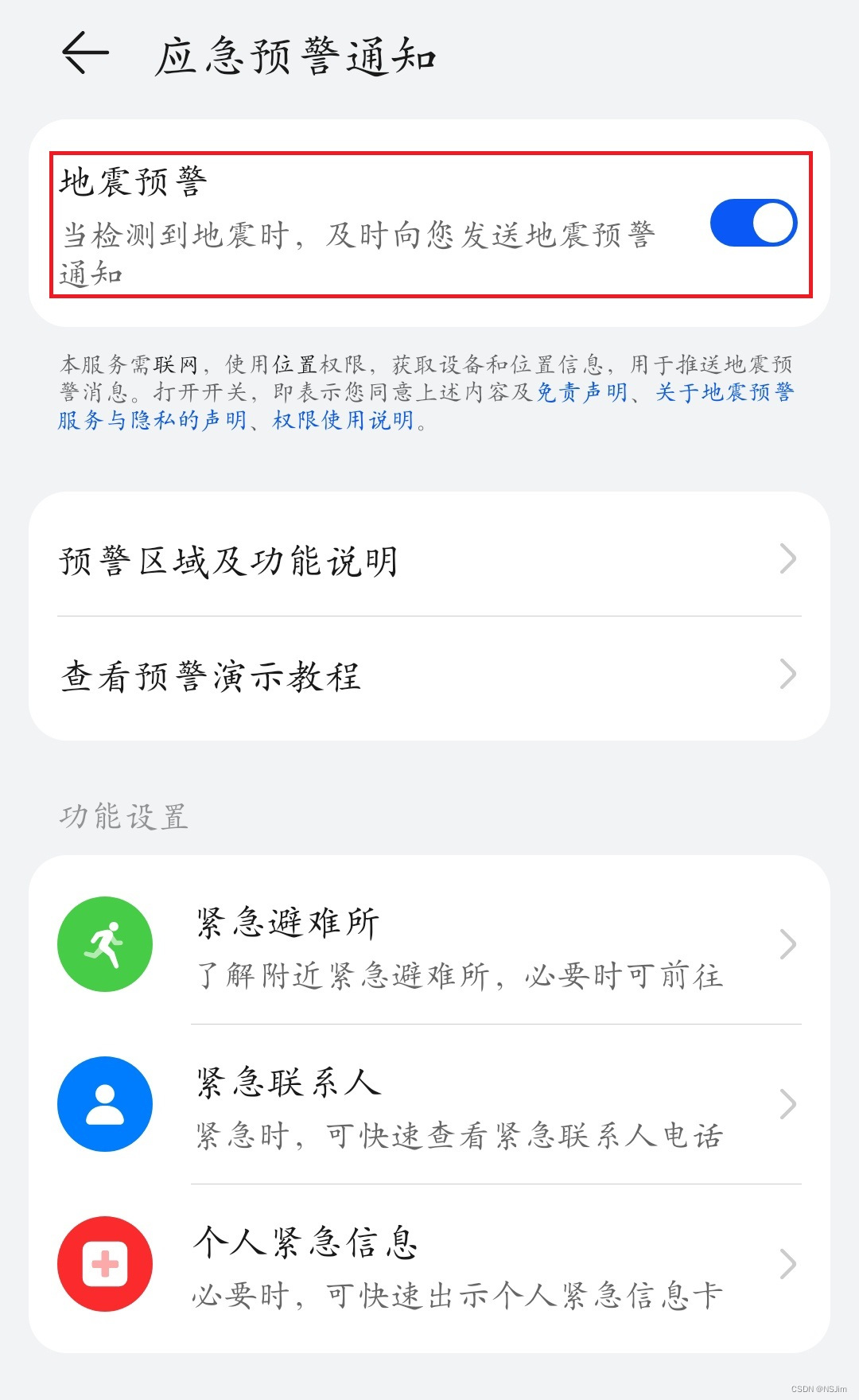
手机开启应急预警通知 / 地震预警
前言 安卓手机在检测到地震时,将发送地震预警通知,但此设置是默认关闭的,原因是以防引发用户恐慌从而引发安全问题,且开启此设置需要完成指引教程,因此默认关闭此设置。下文介绍如何开启此设置。 开启方法 华为手机开…...

2020年12月 Python(一级)真题解析#中国电子学会#全国青少年软件编程等级考试
一、单选题(共25题,每题2分,共50分) 第1题 执行语句print(10==10.0)的结果为? A:10 B:10.0 C:True D:False 正确的答案是 C:True。 解析:在Python中,比较运算符 “==” 用于比较两个值是否相等。在这个特定的比较中,整数10和浮点数10.0在数值上是相等的。…...

遇到无法复现的 Bug
当我们在软件开发过程中遇到无法复现的 Bug 时,这可能会让我们感到头疼和困惑。处理这种 Bug 需要一些技巧和方法来帮助我们更好地解决问题。本篇博客将为大家总结一些常用的技术手段和策略,希望能对开发者们在日常工作中遇到类似问题时提供一些帮助。 …...
)
虚拟列表的实现(简单易懂)
起因: app开发过程中遇到需要渲染3000行的列表,页面直接卡顿,所以开始研究起虚拟列表 实现前提条件: item项等高列表 实现思路: 首先是dom结构: 定义一个容器(固定高度)&#…...

【WordPress】如何在WordPress中实现真·页面路由
这篇文章也可以在我的博客中查看 页面路由 是什么 页面路由是指从url顺着网线砍到网站内容的途径,说人话就是地址与页面的映射。 就像真实世界的地址一样,我要找你,必须知道你的地址。 在网站中,通过地址找内容的机制…...
Android界面设计与用户体验
Android界面设计与用户体验 1. 引言 在如今竞争激烈的移动应用市场,提供优秀的用户体验成为了应用开发的关键要素。无论应用功能多么强大,如果用户界面设计不合理,用户体验不佳,很可能会导致用户流失。因此,在Androi…...
:音画同步)
基于 FFmpeg 的跨平台视频播放器简明教程(八):音画同步
系列文章目录 基于 FFmpeg 的跨平台视频播放器简明教程(一):FFMPEG Conan 环境集成基于 FFmpeg 的跨平台视频播放器简明教程(二):基础知识和解封装(demux)基于 FFmpeg 的跨平台视频…...
)
【NLP pytorch】基于BiLSTM-CRF模型医疗数据实体识别实战(项目详解)
基于BiLSTM-CRF模型医疗数据实体识别实战 1数据来源与加载1.1 数据来源1.2 数据类别名称和定义1.3 数据介绍2 模型介绍2 数据预处理2.1 数据读取2.2 数据标注2.3 数据集划分2.4 词表和标签的生成3 Dataset和DataLoader3.1 Dataset3.2 DataLoader4 BiLSTM模型定义5 CRF模型6 模型…...
)
人工智能原理(1)
*请注意,本文仅供学习使用* 目录 一、人工智能发展 1、孕育期 2、摇篮期 3、形成期 4、发展期(1970-1979) 5、实用期 6、稳步发展期 二、何为人工智能 1、智能的主要观点 2、智能定义 3、人工智能定义 三、人工智能研究方法 1、…...

预测成真,国内传来三个消息,中国年轻人变了,创新力产品崛起
中国的年轻人真的变了! 最近,国内传来三个消息,让外媒的预测成真。 第一,奥迪要开始用国产车的平台了。这里需要说明的是新能源汽车,奥迪也曾多次公开表示,承认了当前中国新能源汽车核心技术上的领先。 第…...
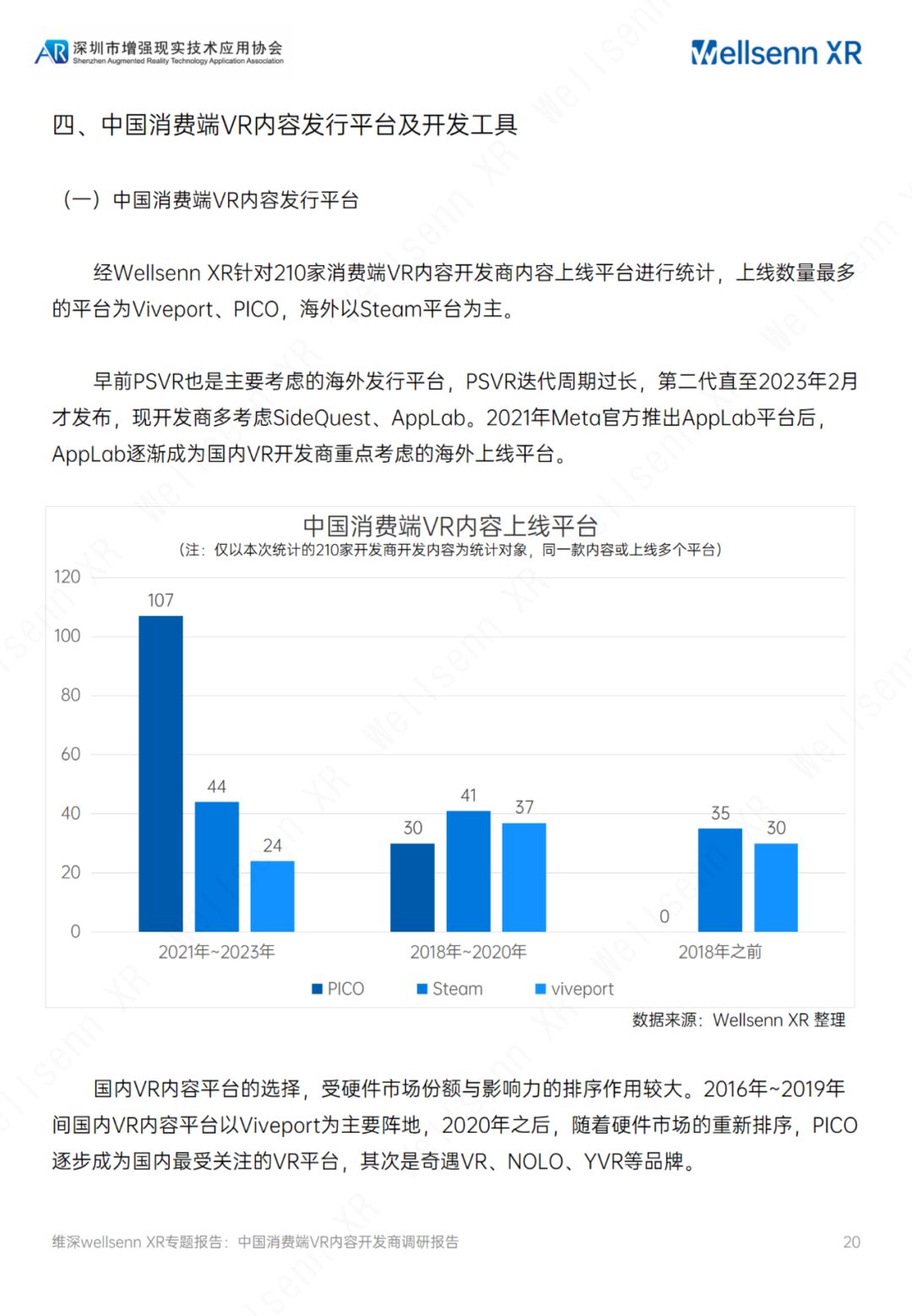
维深(Wellsenn):2023中国消费端VR内容开发商调研报告(附下载
关于报告的所有内容,公众【营销人星球】获取下载查看 核心观点 国内互联网大厂商入局VR,字节跳动、网易表态明确。字节跳动2021年收购国内头部VR硬件厂商PICO后,加速构建VR内容生态,2021年 成立海南创见未来当前已推出VR视频应用…...

redis事务管理详解
事务管理 事务管理乐观锁与悲观锁watch命令实现乐观锁watch命令示例 事务管理 Redis 提供了事务管理功能,可以通过 Redis 的 MULTI、EXEC、WATCH 和 DISCARD 命令来实现。 开启事务: 使用 MULTI 命令开始一个事务,表示接下来执行的命令都属于…...

国产低功耗蓝牙HS6621CxC/6621Px系列支持Find My网络功能方案芯片
目录 什么是“Find My“?HS6621系列简介 什么是“Find My“? “Find My”是苹果公司于19年前推出的针对失物追踪,Find My iPhone(查找我的iPhone)和Find My Friends(查找朋友)的结合体应用。为…...

【openGauss】分区表的介绍与使用
一、openGauss分区表介绍 在openGauss中,数据分区是在一个节点内部对数据按照用户指定的策略做进一步的水平分表,将表中的数据按照指定方式划分为多个互不重叠的部分。 对于大多数用户使用场景,分区表和普通表相比具有以下优点: …...
代码随想录算法训练营day57
文章目录 Day57回文子串题目思路代码 最长回文子序列题目思路代码 Day57 回文子串 647. 回文子串 - 力扣(LeetCode) 题目 给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。 回文字符串 是正着读和倒过来读一样的字符串。…...

【基础类】—前后端通信类系统性学习
一、什么是同源策略及限制 同源策略限制从一个源加载的文档或脚本如何与来自另一个源的资源进行交互。这是一个用于隔离潜在恶意文件的关键的安全机制。源:协议、域名和端口, 默认端口是80 三者有一个不同,即源不同,就是跨域 ht…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
