[数据结构]---八大经典排序算法详解

🐧作者主页:king&南星
🏰专栏链接:c++

文章目录
- 一、八大排序算法复杂度对比
- 二、基于比较的排序算法
- 1.冒泡排序
- 2.选择排序
- 3.插入排序
- 4.希尔排序
- 5.直观感受四种算法的时间复杂度
- 三、基于非比较的排序算法
- 1.基数排序
- 2.箱(桶)排序
- 四、递归比较排序算法
- 1.快速排序
- 2.归并排序
- 1.普通归并
- 2.归并递归
一、八大排序算法复杂度对比

二、基于比较的排序算法
1.冒泡排序
- 介绍:冒泡排序(Bubble Sort),是一种计算机科学领域的较简单的排序算法。
它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果顺序(如从大到小、首字母从Z到A)错误就把他们交换过来。走访元素的工作是重复地进行,直到没有相邻元素需要交换,也就是说该元素列已经排序完成。
这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名“冒泡排序”
-
核心:
冒泡排序:
比较 NUM-1轮,每轮NUM-1次,
每轮(相邻两个比较,不符合要求则交换)
找出一个最大的或者一个最小的

//冒泡排序
void bubble_sort(int* a, int len)
{int t;for ( int i = 0; i < len-1; i++) //len-1轮{for( int j = 0; j < len-1-i ; j++ ) //每轮为无序的元素个数-1次{if ( a[j] > a[j+1] ) //不符合规则交换{t = a[j];a[j] = a[j + 1];a[j + 1] = t;}}}
}
总结:
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度:O( N2)
- 空间复杂度:O(1)
- 稳定性:稳定
2.选择排序
-
介绍:选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。
-
核心:
选择排序:
先假设待排数组第一个为最小值
选择NUM-1轮,每轮从待排数组中选最小的,与第一个进行比较,决定放不放到待排数组第一个
循环从待排数组中找到最小的,记录其下标
交换

//选择排序
void select_sort(int* a, int len)
{int t;int minIndex;for (int i = 0; i < len-1; i++) //len-1轮{//从待排数组中(i ----- len-1)找到最小的minIndex = i; //先假设待排数组中的第一个最小for (int j = i+1; j < len; j++){minIndex = a[j] > a[minIndex] ? minIndex : j;}//符合条件和待排数组中的第一个元素(i)交换if ( a[minIndex] < a[i] ){t = a[minIndex];a[minIndex] = a[i];a[i] = t;}}
}
总结:
- 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:O(N2)
- 空间复杂度:O(1)
- 稳定性:不稳定
3.插入排序
-
介绍:插入排序,一般也被称为直接插入排序。对于少量元素的排序,它是一个有效的算法 。插入排序是一种最简单的排序方法,它的基本思想是将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增1的有序表。在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动。
核心:
插入排序:
设置第一个为有序数组,右边NUM-1个为待插数据
然后NUM-1轮,每轮把一个数据插入到有序数组中
插入方式:
1. 先临时保存待插数据
2. 然后从待插数据前一个开始往前循环(越界循环结束)
比待插数据大则往后覆盖,比待插数据小则循环结束
3. 用待插数据覆盖回来(第二步结束后下标的下一个位置)

插入部分图解

//插入排序
void insert_sort(int* a, int len)
{int j;int temp;//保存待插数据for (int i = 1; i < len; i++) //len-1轮{temp = a[i]; //待插数据前一个开始往前循环(越界循环结束)for ( j = i-1 ; j >= 0 ; j-- ) {//比待插数据大则往后覆盖if ( a[j] > temp ) a[j + 1] = a[j];else break;}//用待插数据覆盖回来(第二步结束后下标的下一个位置)a[j + 1] = temp;}
}
总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N2)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
4.希尔排序
-
介绍:
-
希尔排序(Shell’s Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因 D.L.Shell 于 1959 年提出而得名。
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至 1 时,整个文件恰被分成一组,算法便终止。
核心:
希尔(shell)排序:
一个叫做shell的科学家发明的
优化后的插入排序
引入步长的概念:
一开始是 len/2 然后每次 除2 到1为止
根据步长来分组,然后组内作插入排序

//希尔排序
void shell_sort(int* a, int len)
{int j, temp;int step = len >> 2;while ( step )//根据步长来分组{//组内作插入排序//从step开始 len-1-step轮for( int i = step ; i < len; i++ ){temp = a[i];//临时保存待插数据//待插数据前一个开始往前循环(越界循环结束)for ( j = i-step; j >= 0 ; j -= step ){//比待插数据大则往后覆盖if (a[j] > temp) a[j + step] = a[j];else break;}//用待插数据覆盖回来(第二步结束后下标的下一个位置)a[j + step] = temp;}step >>= 1;}
}
总结:
- 希尔排序是对直接插入排序的优化。
- 当step > 1时都是预排序,目的是让数组更接近于有序。当step == 1时,数组已经接近有序的 了,这样就会很快。这样整体而言,可以达到优化的效果。
- 希尔排序的时间复杂度不好计算,需要进行推导,推导出来平均时间复杂度: O(N1.3— N2)
- 稳定性:不稳定
5.直观感受四种算法的时间复杂度
这里随机产出100000个数字,利用上面4种排序算法进行排序,结果如下,可以看到希尔排序仅仅用了16ms

#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#include <windows.h>
//数据个数
#define NUM 100000void init(int* a, int len);
void bubble_sort(int* a, int len);
//选择排序
void select_sort(int* a, int len);
//插入排序
void insert_sort(int* a, int len);
//希尔排序
void shell_sort(int* a, int len);int main() {ULONGLONG oldTime, newTime;srand(time(NULL));int arr[NUM];init(arr, NUM);//初始化//获取排序前时间oldTime = GetTickCount64();bubble_sort(arr, NUM);//排序//获取排序后时间newTime = GetTickCount64();printf("bubble_sort:%llu\n", newTime - oldTime);init(arr, NUM);oldTime = GetTickCount64();select_sort(arr, NUM);newTime = GetTickCount64();printf("select_sort:%llu\n", newTime - oldTime);init(arr, NUM);oldTime = GetTickCount64();insert_sort(arr, NUM);newTime = GetTickCount64();printf("insert_sort:%llu\n", newTime - oldTime);init(arr, NUM);oldTime = GetTickCount64();shell_sort(arr, NUM);newTime = GetTickCount64();printf("shell_sort:%llu\n", newTime - oldTime);while (1);return 0;
}
void init(int* a, int len) {for (int i = 0; i < len; i++)a[i] = rand() % 1000;
}
//希尔排序
void shell_sort(int* a, int len) {int step = len / 2;int temp;int j;while (step) {//分组//组内做插入排序for (int i = step; i < len; i++) {//每次循环插入a[i]temp = a[i];//临时存储待插数据for (j = i - step; j >= 0 && a[j] > temp; j -= step) {//从前往后覆盖a[j + step] = a[j];}a[j + step] = temp;}step /= 2;//每次步长变成原来的一半}
}//插入排序
void insert_sort(int* a, int len) {int temp;int j;for (int i = 1; i < len; i++) {//每次循环插入a[i]//把a[i] 插入到 a[0] - a[i-1] 数组中去temp = a[i];//临时存储待插数据for (j = i - 1; j >= 0 && a[j] > temp; j--) {//从前往后覆盖a[j + 1] = a[j];}//插入进来a[j + 1] = temp;}
}
//选择排序
void select_sort(int* a, int len) {int min_idx;//记录最小的元素的下标int temp;for (int i = 0; i < len - 1; i++) {//找len-1次//每次 找出 a[i] - a[len-1] 范围内最小的元素 min_idx = i;//假设a[i]最小for (int j = i; j < len; j++) {min_idx = ((a[min_idx] < a[j]) ? min_idx : j);}//a[min_idx] 和 a[i]交换temp = a[i];a[i] = a[min_idx];a[min_idx] = temp;}
}void bubble_sort(int* a, int len) {int temp;for (int j = 0; j < len - 1; j++) {for (int i = 0; i < len - j - 1; i++) {//0 - len-2if (a[i] > a[i + 1]) {//不符合要求//交换temp = a[i];a[i] = a[i + 1];a[i + 1] = temp;}}}
}
三、基于非比较的排序算法
1.基数排序
-
介绍:基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或bin sort,顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些“桶”中,藉以达到排序的作用,基数排序法是属于稳定性的排序,其时间复杂度为O (nlog®m),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的稳定性排序法。
核心:
基数排序 :O(n)
最快的排序方式 没有之一
利用数组下标天然有序的特性来进行排序
max:最大元素值
限制很多:1. 只能排正整数(优化后可以对所有整数排序) 2. 不能有重复 3. 空间可能耗费特别大 4. 临时空间大小

//基数排序
void radix_sort(int* a, int len, int max)
{int index = 0;//先准备一个临时数组 max+1int* pTemp = (int*)malloc(sizeof(int) * (max + 1));assert(pTemp); //判断申请成功没//初始化为-1//for (int i = 0; i <= max; i++) pTemp[i] = -1;memset(pTemp, -1, sizeof(int) * (max + 1));//将待排数组放到临时数组中,待排数组的值作为临时数组的下标for (int i = 0; i < len; i++) pTemp[a[i]] = a[i];//从临时数组中把排序好的数据放回原数组中for (int i = 0; i <= max; i++) {if ( pTemp[i] != -1 ){a[index++] = pTemp[i];}}//释放内存free(pTemp);
}
总结:
- 时间复杂度:O(n+k)
- 空间复杂度:O(n+k)
- 不能对小数进行排序,但是速度极快
2.箱(桶)排序
-
介绍:桶排序 (Bucket sort)或所谓的箱排序,是一个排序算法,工作的原理是将数组分到有限数量的桶子里。每个桶子再个别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序)。桶排序是鸽巢排序的一种归纳结果。当要被排序的数组内的数值是均匀分配的时候,桶排序使用线性时间(Θ(n))。但桶排序并不是 比较排序,他不受到 O(n log n) 下限的影响。
核心:
桶(箱)排序:bucket_sort
把数据分成若干个箱子 然后箱子里用其他排序

这里是按个位十位分箱,内部类似于基数排序
//箱排序
void bucket_sort(int* a, int len)
{int idx, k;int n = 1; int* pTemp = NULL;while ( n < AREA )//1000以内的数字,AREA ==1000{//1 做箱子 并初始化箱子pTemp = (int*)malloc(10 * len * sizeof(int));for (int i = 0; i < 10 * len; i++) pTemp[i] = -1;//2 根据特性(对应位作为箱子的编号)放入箱子中for (int i = 0; i < len; i++){//获取到数据这一轮要看的位上的数据idx = a[i] / n % 10;pTemp[idx * len + i] = a[i];}//3 从箱子中取出,覆盖a数组k = 0;for (int i = 0; i < 10*len; i++){if ( pTemp[i] != -1 )a[k++] = pTemp[i];}//4 销毁箱子free(pTemp);pTemp = NULL;n *= 10;}
}
四、递归比较排序算法
1.快速排序
-
介绍:快速排序(Quicksort),计算机科学词汇,适用领域Pascal,c++等语言,是对冒泡排序算法的一种改进。
核心:
快速排序:就是分组排序
把数据分成两组
确定中间值,左边都比中间值小 右边都比中间值大
递归(递推)持续分组 到 不可再分(一组只有一个数据)为止

void Quick_sort(int* a, int len)
{quick_sort(a, 0, len - 1);
}
void quick_sort(int* a, int Left, int Right)
{int L = Left, R = Right;if ( L >= R ) return; //递归结束// 先假设a[left]是中间数据,并临时保存int temp = a[L];// 循环挪动l和r并覆盖 循环结束后 L==Rwhile ( L < R ){// 先挪右边的while ( L < R && a[R] > temp) R--;a[L] = a[R];// 再挪左边的while (L<R && a[L] < temp ) L++;a[R] = a[L];}// 用中间数据覆盖回来a[L] = temp; //a[R] = temp;quick_sort(a, Left, R - 1);quick_sort(a, L + 1, Right);
}
2.归并排序
- 介绍:归并排序是建立在归并操作上的一种有效,稳定的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
1.普通归并
- 核心:两个有序数组合并成一个有序数组

void Merge_sort(int* a, int L, int M, int R)
{int Left = L, Right = M + 1;if (L >= R) return;//开临时内存int* pTemp = (int*)malloc(sizeof(int) * (R - L + 1));int k = 0;//两个中有一个放完了while ( Left <= M && Right <= R ){if (a[Left] < a[Right]) pTemp[k++] = a[Left++];else pTemp[k++] = a[Right++];}//左边还没放完if (Left <= M) memcpy(pTemp + k, a + Left, sizeof(int) * (M - Left + 1));//右边还没放完else memcpy(pTemp + k, a +Right, sizeof(int) * (R - Right + 1));//覆盖回去memcpy( a + L , pTemp, sizeof(int) * (R - L + 1));//释放内存free(pTemp);
}
2.归并递归
- 核心:把无序数组完全拆开,再进行归并排序

void Merge_Sort(int* a, int len)
{merge__sort(a, 0, len - 1);
}
void merge__sort(int* a, int L, int R)
{// L和R不相等,说明还没拆到只剩一个,继续拆if (L < R){int m = L + (R - L) / 2;merge__sort(a, L, m); //左边一半merge__sort(a, m + 1, R); //右边一半Merge_sort(a, L, m, R); //拆到无法拆了就合并}
}
🎉欢迎各位→点赞👏 + 收藏💞 + 留言🔔
💬总结:希望你看完之后,能对你有所帮助,不足请指正!共同学习交流 🐾
相关文章:

[数据结构]---八大经典排序算法详解
🐧作者主页:king&南星 🏰专栏链接:c 文章目录一、八大排序算法复杂度对比二、基于比较的排序算法1.冒泡排序2.选择排序3.插入排序4.希尔排序5.直观感受四种算法的时间复杂度三、基于非比较的排序算法1.基数排序2.箱(桶)排序四…...
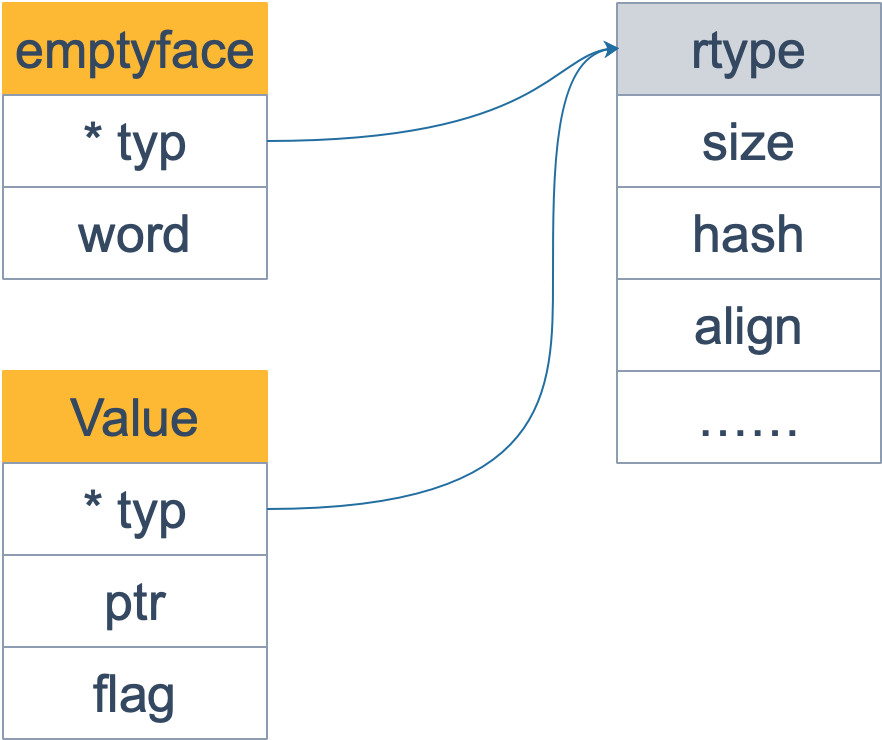
Go语言设计与实现 -- 反射
Go的反射有哪些应用? IDE中代码的自动补全对象序列化fmt函数的相关实现ORM框架 什么情况下需要使用反射? 不能明确函数调用哪个接口,需要根据传入的参数在运行时决定。不能明确传入函数的参数类型,需要在运行时处理任意对象。 …...

利用5G工业网关实现工业数字化的工业互联网解决方案
5G工业网关是一种用于将工业生产环境中的数据连接到工业互联网的解决方案。它可以利用高带宽、高速率、低时延的5G网络连接工业现场的PLC、传感器、工业设备和云端数据中心,从而实现工业数字化。 物通博联工业互联网解决方案 物通博联5G工业网关的使用步骤&#x…...
朋友当上项目测试组长了,我真的羡慕了
最近我发现一个神奇的事情,我一个朋友居然已经当上了测试项目组长,据我所知他去年还是在深圳的一家创业公司做苦逼的测试狗,短短8个月,到底发生了什么? 于是我立刻私聊他八卦一番。 原来他所在的公司最近正在裁员&am…...
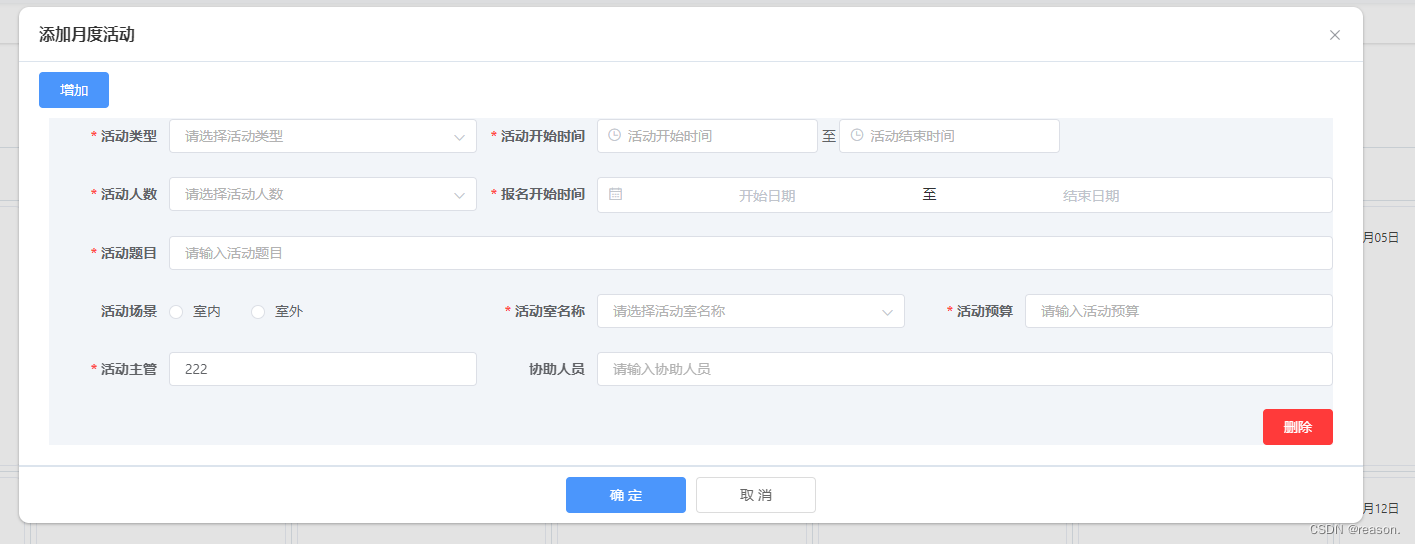
element-ui实现动态添加表单项并实现事件触发验证验证
需求分析:点击新增后新增一个月度活动详情,提交时可同时提交多个月度活动详情。点击某一个月度活动信息的删除后可删除对应月度活动信息 H5部分: <el-dialog :title"title" :visible.sync"open" append-to-body>…...
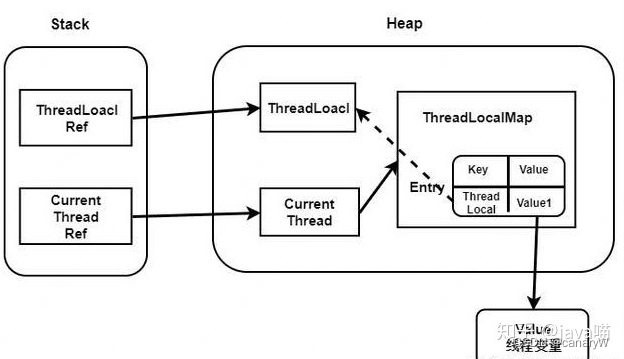
ThreadLocal 内存泄漏问题
1. 认识ThreadLocal java中提高了threadlocal,为每个线程保存其独有的变量,threadlocal使用的一个小例子是: public class ThreadLocalTest {public static void main(String[] args) {ThreadLocal<String> threadIds new ThreadLoc…...
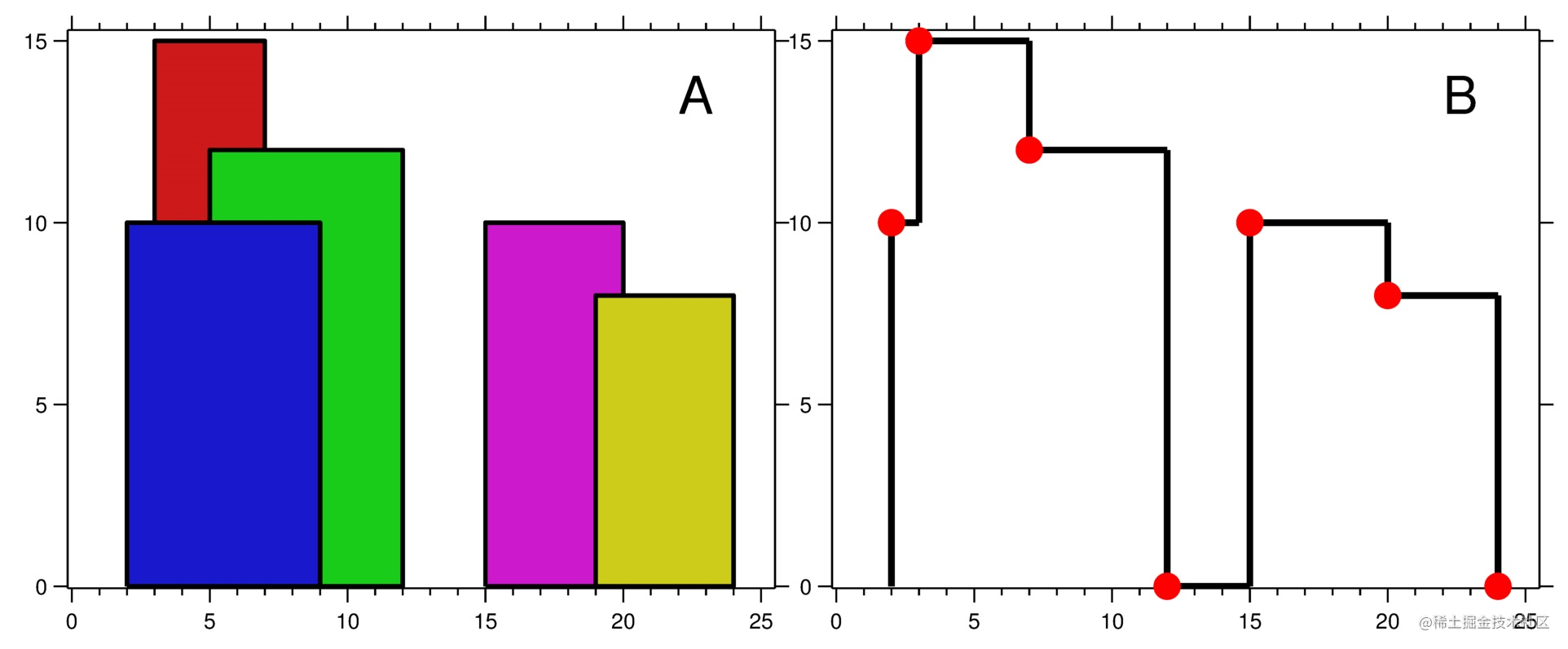
【算法】两道算法题根据提供字母解决解码方法和城市的天际线天际线问题
算法目录解码方法Java解答参考:天际线问题Java解答参考:大家好,我是小冷。 上一篇了解了项目相关的知识点 接下来看下两道算法题吧,用Java解答,可能更能激发一下大脑思考。 解码方法 题目要求: 一条包含…...

Python-TCP网络编程基础以及客户端程序开发
文章目录一. 网络编程基础- 什么是IP地址?- 什么是端口和端口号?- TCP介绍- socket介绍二. TCP客户端程序开发三. 扩展一. 网络编程基础 - 什么是IP地址? IP地址就是标识网络中设备的一个地址 IP地址分为 IPv4 和 IPv6 IPv4使用十进制, IPv6使用十六进制 查看本机IP地址: l…...

超低成本DDoS攻击来袭,看WAF如何绝地防护
一、DDoS攻击,不止于网络传输层 网络世界里为人们所熟知的DDoS攻击,多数是通过对带宽或网络计算资源的持续、大量消耗,最终导致目标网络与业务的瘫痪;这类DDOS攻击, 工作在OSI模型的网络层与传输层,利用协…...
)
CF1795E Explosions? (单调栈)
传送门 题意: 有 n 个怪兽需要消灭,它们的生命值分别是 h [1],h [2]......h [n]. 我们可以使用两种技能: 技能 1:选择任意一个怪兽,使其生命值降低 1 点,并且需要 1 点能量值. 技能 2:选择任意…...
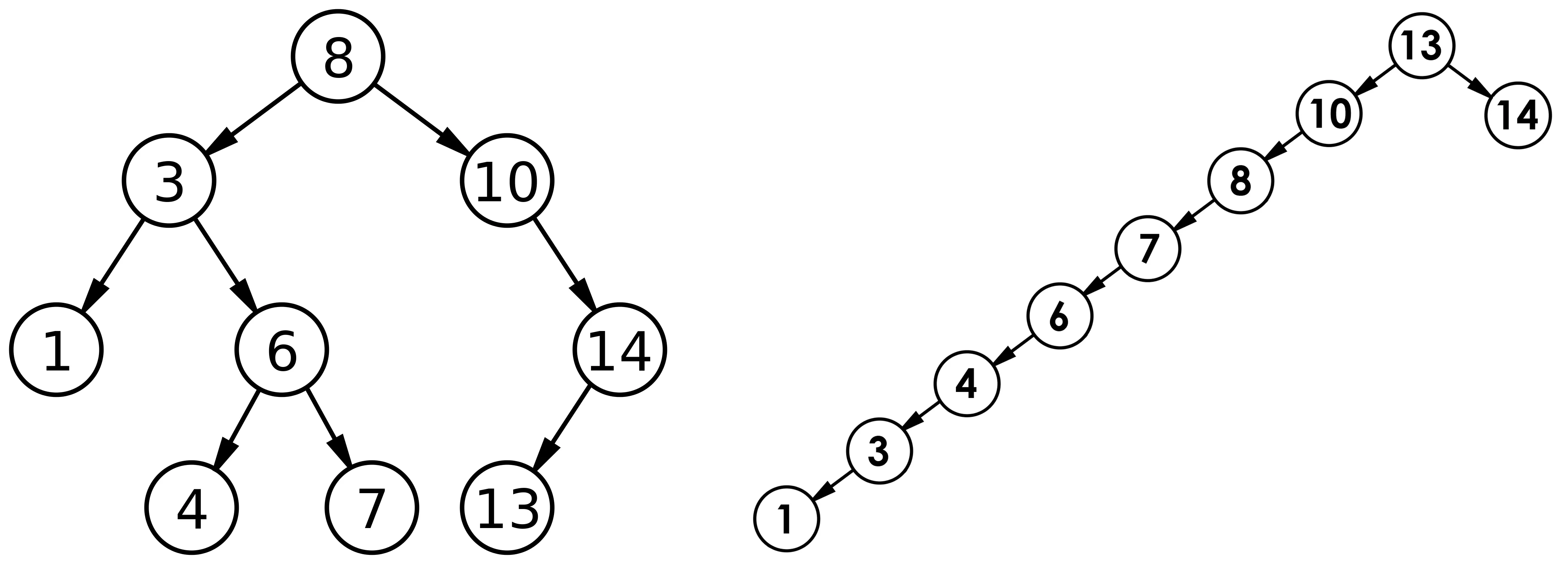
C++——二叉树排序树
文章目录1 二叉搜索树概念2 二叉搜索树操作与模拟实现2.1 二叉搜索树的查找非递归版本递归版本2.2 二叉搜索树的插入非递归版本递归版本2.3 二叉搜索树的删除非递归版本递归版本3 二叉搜索树的应用(K模型、KV模型)4 二叉搜索树的性能分析1 二叉搜索树概念…...
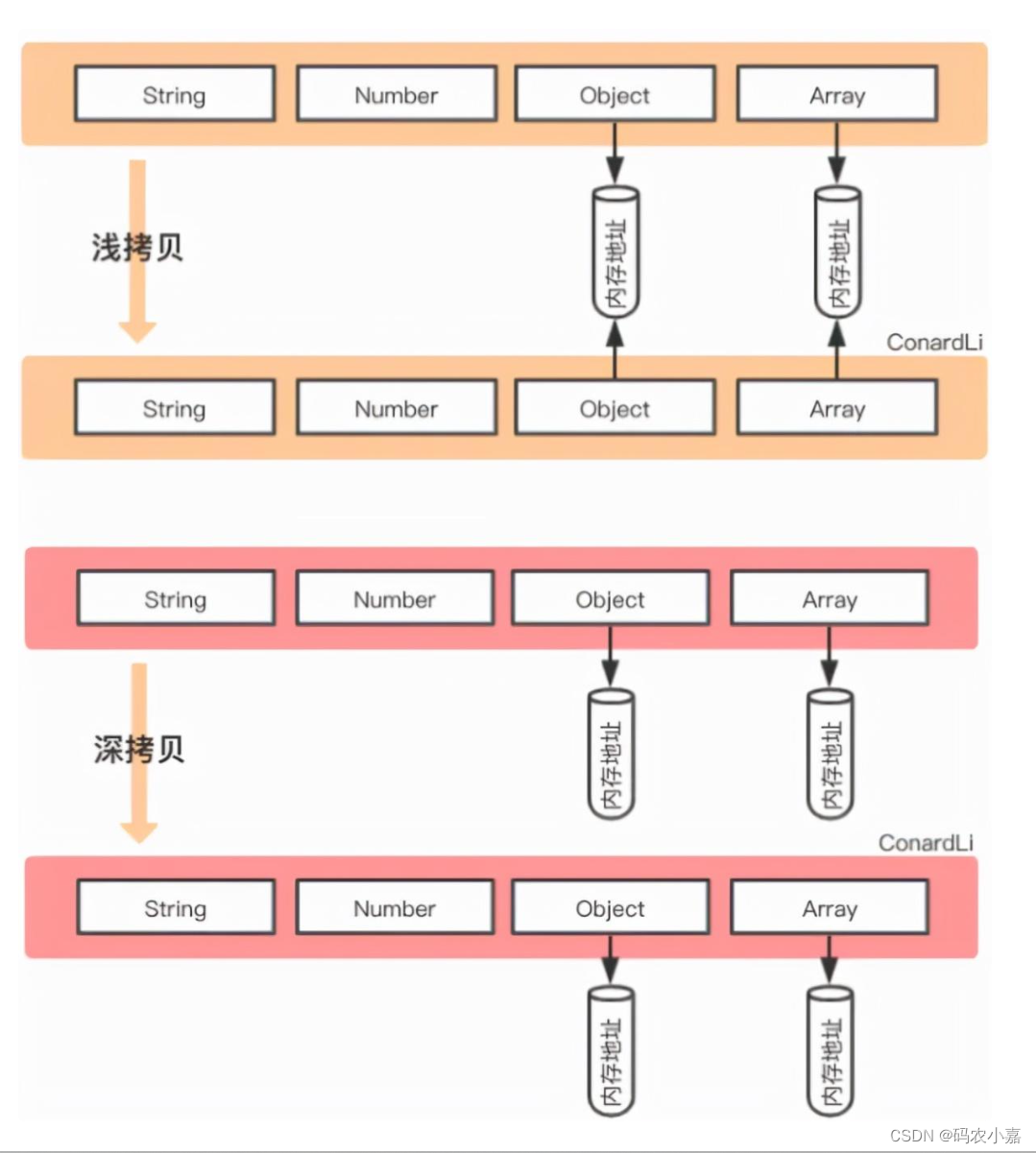
深拷贝浅拷贝的区别?如何实现一个深拷贝?
一、数据类型存储 JavaScript中存在两大数据类型: 基本类型 Number String null Undefined Boolean symbol引用类型 array object function 基本类型数据保存在在栈内存中 引用类型数据保存在堆内存中,引用数据类型的变量是一个指向堆内存中实际对象的…...
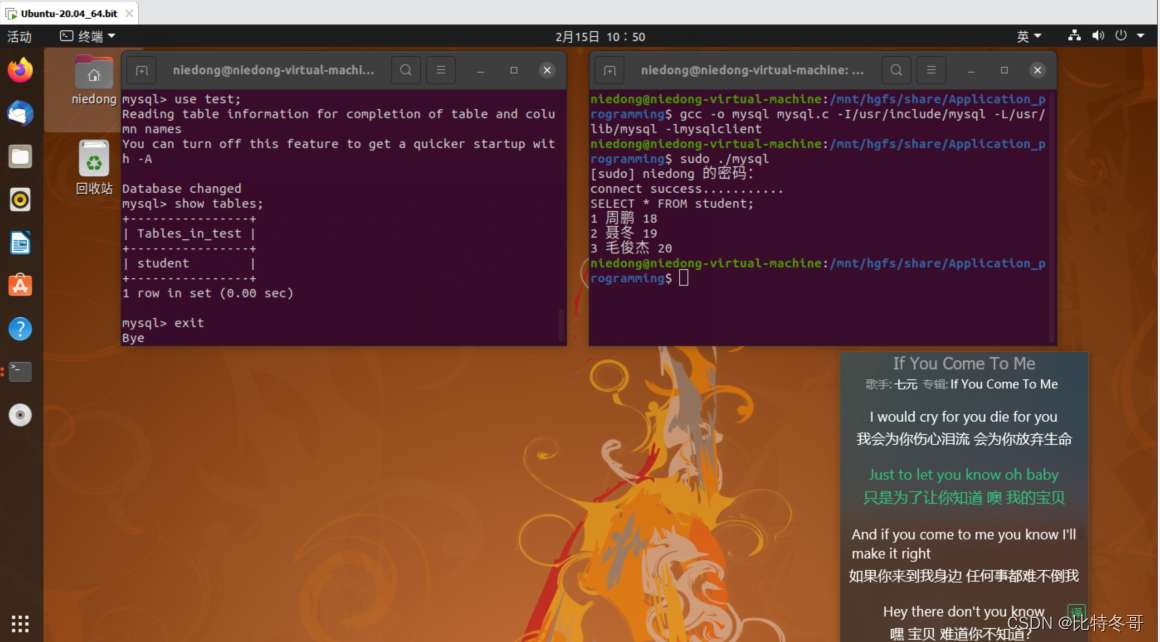
Linux应用编程下连接本地数据库进行增删改查系列操作
文章目录前言一、常用SQL操作语句二、相关函数解析三、连接本地数据库四、编译运行五、程序源码前言 本篇为C语言应用编程下连接Linux本地数据库进行增删改查系列操作。 在此之前,首先当然是你需要具备一定的数据库基础,所以下面我先列出部分常用的SQL…...

图论学习03
图神经网络模型介绍 将图神经网络分为基于谱域上的模型和基于空域上的模型,并按照发展顺序详解每个类别中的重要模型。 基于谱域的图神经网络 谱域上的图卷积在图学习迈向深度学习的发展历程上起到了关键性的作用。三个具有代表性的谱域图神经网络 谱图卷积网络切…...

解决qt中cmake单独存放 .ui, .cpp, .h文件
设想 项目文件较多,全部放在一个目录下就像依托答辩。 希望能将头文件放入include,ui文件放入ui,源文件放入src。 为了将Qt代码和一般非Qt代码分离开,进一步地: 将Qt源文件放入qt_src,普通源文件放入sr…...

操作系统(day12)-- 基本分段存储,段页式存储
基本分段存储管理方式 不会产生内部碎片,会产生外部碎片 分段 按照程序自身的逻辑关系划分为 若干个段,每个段都有一个段名,每段从0开始编址 分段存储管理方式中一个段表项由段号(隐含)、段长、基地址 分段的段表项固…...

疯狂弹出请插入多卷集的最后一张磁盘窗口
整个人嘛了,今天插上U盘,跟tmd中了病毒一样, 屏幕疯狂弹出窗口, 提示请插入多卷集的最后一张磁盘! 点确定之后他继续弹出,点取消它也继续弹出, 关掉一个又弹出来一个,妈的&#x…...
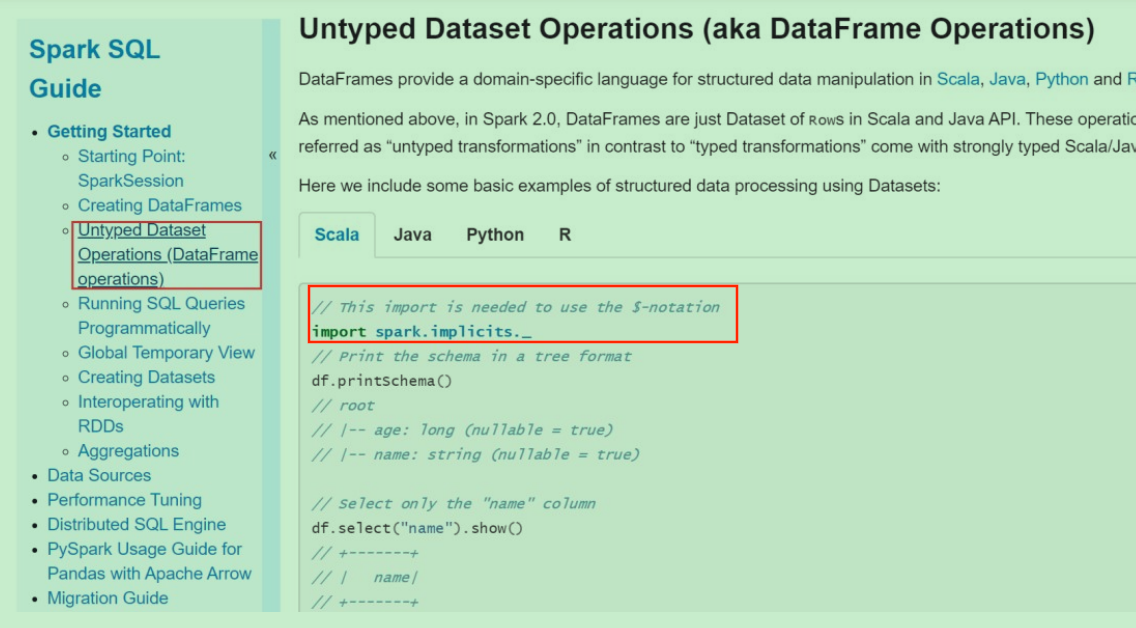
Spark12: SparkSQL入门
一、SparkSQL Spark SQL和我们之前讲Hive的时候说的hive on spark是不一样的。hive on spark是表示把底层的mapreduce引擎替换为spark引擎。而Spark SQL是Spark自己实现的一套SQL处理引擎。Spark SQL是Spark中的一个模块,主要用于进行结构化数据的处理。它提供的最核…...

show profile和trance分析SQL
目录 一.show profile分析SQL 二.trance分析优化器执行计划 一.show profile分析SQL Mysql从5.0.37版本开始增加了对show profiles和show profile语句的支持。show profiles能够在做SQL优化时帮助我们了解时间都耗费到哪里去了。。 通过have_profiling参数,能够…...
[AI生成图片] 效果最好的Midjourney 的介绍和使用
Midjourney介绍: 是一个文本生成图片的扩散模型,能够根据输入的任何文本生成令人难以置信的图像,让数十亿人在几秒钟内创造惊人的艺术。为方便用户控制和快速生成图片,打开后在页面底部输入文本内容,稍等一小会&#…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
