数论 —— 高斯记号(Gauss mark)
定义
数学上,高斯记号(Gauss mark)是指对取整符号和取小符号的统称,用于数论等领域。
- 设 x∈Rx \in \textbf{R}x∈R,用 [x][x][x] 表示不超过 xxx 的最大整数。也可记作 [x][x][x]。
- 设 x∈Rx \in \textbf{R}x∈R,用 {x}\{x\}{x} 表示 xxx 的非负纯小数,即 {x}=x-[x]\{x\}=x-[x]{x}=x-[x]。
例如
- [1]=1
- [0]=0
- [-1]=-1
- [-1.2]=-2
- {1.5}=0.5
- {-1.5}=0.5
- {-1.2}=0.8
性质
- 对于任意实数 x,x=[x]+{x}
- x-1<[x]≤x<[x]+1
- [n+x]=n+[x],n 为整数
- [x]+[y]≤[x+y]≤[x]+[y]+1
例题
解方程 x+2{x}=3[x]x+2\{x\}=3[x]x+2{x}=3[x]
思路
使用定义 x=[x]+{x}
解题
根据定义 x=[x]+{x},带入原方程变为 [x]+3{x}=3[x]
2[x]=3{x}
∵0≤{x}<1\because 0≤\{x\}<1∵0≤{x}<1
∴0≤3{x}<3\therefore 0≤3\{x\}<3∴0≤3{x}<3
∵[x]\because [x]∵[x] 一定是一个整数。
∴3{x}=0,1,2\therefore 3\{x\}=0,1,2∴3{x}=0,1,2
∵2[x]\because 2[x]∵2[x] 一定是一个偶数。
∴3{x}=0,2\therefore 3\{x\}=0,2∴3{x}=0,2
带入原式进行讨论。
- 当 3{x}=03\{x\}=03{x}=0 的时候,{x}=0\{x\}=0{x}=0,对应 [x]=0[x]=0[x]=0,即 x=0x=0x=0。
- 当 3{x}=23\{x\}=23{x}=2 的时候,{x}=23\{x\}=\frac{2}{3}{x}=32,对应 [x]=1[x]=1[x]=1,即 x=53x=\frac{5}{3}x=35。
解方程 [x]{x}+x=2{x}+10[x]\{x\}+x=2\{x\}+10[x]{x}+x=2{x}+10
思路
根据性质,可得 0≤{x}<10≤\{x\}<10≤{x}<1。
我们可以将方程变成 {x}=...\{x\}=...{x}=... 形式。
解题
根据定义 x=[x]+{x},带入原方程变为 [x]{x}+[x]+{x}=2{x}+10
合并同类项
[x]{x}-{x}=10-[x]
{x}([x]-1)=10-[x]
{x}=10−[x][x]−1\{x\} = \frac{10-[x]}{[x]-1}{x}=[x]−110−[x]
∵0≤{x}<1\because 0≤\{x\}<1∵0≤{x}<1
∴0≤10−[x][x]−1<1\therefore 0≤\frac{10-[x]}{[x]-1}<1∴0≤[x]−110−[x]<1
由于分子分母都含有 [x][x][x],因此需要对分母进行配方。
10−[x][x]−1=9+1−[x][x]−1=9−([x]−1)[x]−1\frac{10-[x]}{[x]-1}=\frac{9+1-[x]}{[x]-1}=\frac{9-([x]-1)}{[x]-1}[x]−110−[x]=[x]−19+1−[x]=[x]−19−([x]−1)
0≤9−([x]−1)[x]−1<10≤\frac{9-([x]-1)}{[x]-1}<10≤[x]−19−([x]−1)<1
0≤9[x]−1−1<10≤\frac{9}{[x]-1}-1<10≤[x]−19−1<1
1≤9[x]−1<21≤\frac{9}{[x]-1}<21≤[x]−19<2
1≥[x]−19>121\ge \frac{[x]-1}{9}>\frac{1}{2}1≥9[x]−1>21
9≥[x]−1>4.59 \ge [x]-1 > 4.59≥[x]−1>4.5
10≥[x]>5.510 \ge [x] > 5.510≥[x]>5.5
∴[x]=6,7,8,9,10\therefore [x]=6,7,8,9,10∴[x]=6,7,8,9,10
带入原式进行讨论。
- 当 [x]=6[x]=6[x]=6 时候,原方程为 x=10−66−1=45{x}=\frac{10-6}{6-1}=\frac{4}{5}x=6−110−6=54,即 x=6.8x=6.8x=6.8。
- 当 [x]=7[x]=7[x]=7 时候,原方程为 x=(10−7)/(7−1)=3/6{x}=(10-7)/(7-1)=3/6x=(10−7)/(7−1)=3/6,即 x=7.5x=7.5x=7.5。
- 当 [x]=8[x]=8[x]=8 时候,原方程为 x=(10−8)/(8−1)=2/7{x}=(10-8)/(8-1)=2/7x=(10−8)/(8−1)=2/7,即 x=8+2/7x=8+2/7x=8+2/7。
- 当 [x]=9[x]=9[x]=9 时候,原方程为 x=(10−9)/(9−1)=1/8{x}=(10-9)/(9-1)=1/8x=(10−9)/(9−1)=1/8,即 x=9.125x=9.125x=9.125。
- 当 [x]=10[x]=10[x]=10 时候,原方程为 x=(10−10)/(10−1)=0{x}=(10-10)/(10-1)=0x=(10−10)/(10−1)=0,即 x=10x=10x=10。
关于 x 的方程 [x2]+[x3]=k[\frac{x}{2}]+[\frac{x}{3}]=k[2x]+[3x]=k 无解的自然数 k 排成一行,其前 2018 个 k 值之和等于多少?
思路
看到 x2\frac{x}{2}2x 和 x3\frac{x}{3}3x,自然想到了周期问题。
解题
222 和 333 的最小公倍数为 2×3=62 \times 3=62×3=6。因此对周期 666 进行枚举。
为了让大家更容易看出周期问题的套路,我们对 0∼110 \sim 110∼11 进行枚举。
| x | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| k=[x2]+[x3]k=[\frac{x}{2}]+[\frac{x}{3}]k=[2x]+[3x] | 0 | 0 | 1 | 2 | 3 | 3 |
| x | 6 | 7 | 8 | 9 | 10 | 11 |
| k=[x2]+[x3]k=[\frac{x}{2}]+[\frac{x}{3}]k=[2x]+[3x] | 5 | 5 | 6 | 7 | 8 | 8 |
如上图。
- x=0x=0x=0 与 x=6x=6x=6 是同周期的。
- x=1x=1x=1 与 x=7x=7x=7 是同周期的。
- .........
- x=5x=5x=5 与 x=11x=11x=11 是同周期的。
这样,我们可以轻易发现周期的规律。
- k=5×n+r,r∈[0,1,2,3]k=5\times n+r,\ r \in [0,1,2,3]k=5×n+r, r∈[0,1,2,3] 方程有解。
- k=5×n+r,r∈[4]k=5\times n+r,\ r \in [4]k=5×n+r, r∈[4] 方程无解。
这样,我们可以构造出所有解的序列为 k=5×n+4,n∈[0,1,2,...]k=5 \times n+4,\ n \in [0,1,2,...]k=5×n+4, n∈[0,1,2,...]。
这样前 201820182018 个 kkk 序列即为 4,9,14,...,5×2017+4=10,0894,9,14,...,5 \times 2017+4=10,0894,9,14,...,5×2017+4=10,089。
本题答案即为 ∑S=4+9+14+...+10089\sum S=4+9+14+...+10089∑S=4+9+14+...+10089。
根据等差数列求和公式可得,首项为 444,公差为 d=5d=5d=5,项数为 201820182018。
∑S=4×2018+2018×2017×52=10,183,837\sum S=4 \times 2018+\frac{2018 \times 2017 \times 5}{2}=10,183,837∑S=4×2018+22018×2017×5=10,183,837
相关文章:
)
数论 —— 高斯记号(Gauss mark)
定义 数学上,高斯记号(Gauss mark)是指对取整符号和取小符号的统称,用于数论等领域。 设 x∈Rx \in \textbf{R}x∈R,用 [x][x][x] 表示不超过 xxx 的最大整数。也可记作 [x][x][x]。设 x∈Rx \in \textbf{R}x∈R&…...

【随笔】程序员眼中的 CPU,“没有灵魂的躯体”
引言 先引用一段比较有意思的论述: 现实中每个人是由两部分构成,灵魂和躯体,灵魂依附于躯体游走于世间,现实中我们面对的每个人其实面对的是其灵魂而非肉体,肉体不过是表象而已。 灵魂本性乃一恶物,寄生于…...

算法的时间复杂度
算法在编写成可执行程序后,运行时需要消耗时间资源和空间(内存)资源,因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的。 时间复杂度主要衡量一个算法运行的快慢,而空间复杂度主要衡量一个算法运…...
 | 机试题算法思路 【2023】)
华为OD机试 - 叠放书籍(Python) | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 寻找路径 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 五键键盘 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - IPv4 地址转换成整数 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 对称美学 | 备考思路,刷题要点,答疑 …...
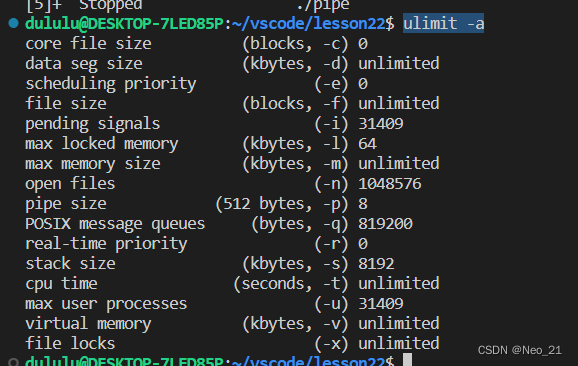
进程间通信(重点)
概念 进程是一个独立的资源分配单元,不同进程之间的资源是独立的进程并非孤立的,不同进程需要进行信息的交互和状态的传递,因此需要进程之间的通信【IPC: Inter processes communication】 如qq聊天,qq在每个人的手机上是独立的…...
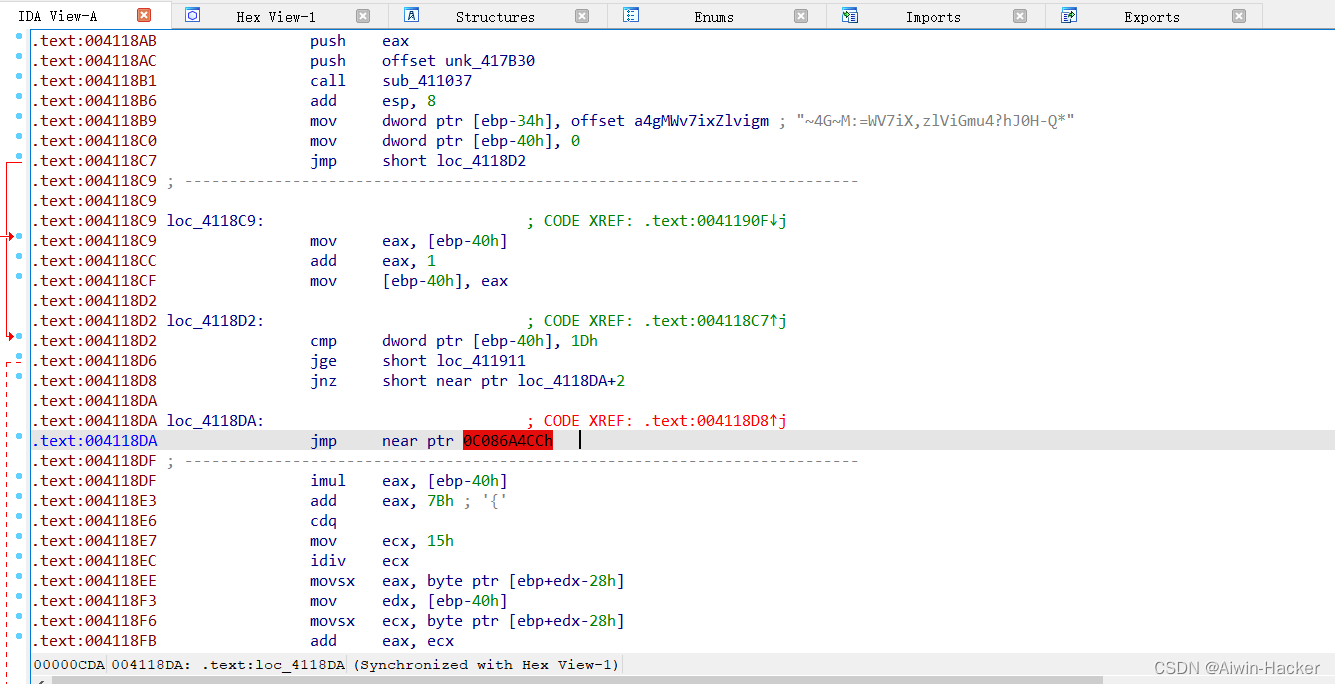
Reverse入门[不断记录]
文章目录前言一、[SWPUCTF 2021 新生赛]re1二、[SWPUCTF 2021 新生赛]re2三、[GFCTF 2021]wordy[花指令]四、[NSSRound#3 Team]jump_by_jump[花指令]五、[NSSRound#3 Team]jump_by_jump_revenge[花指令]前言 心血来潮,想接触点Reverse,感受下Reverse&am…...
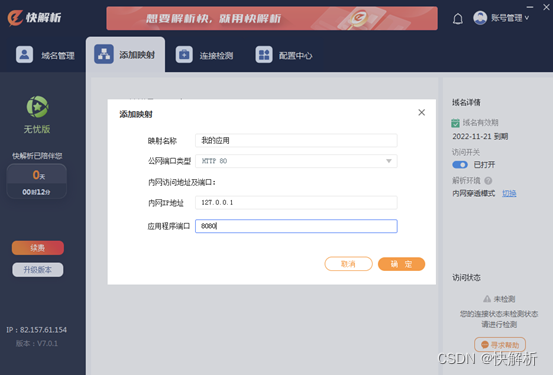
如何实现外网访问内网ip?公网端口映射或内网映射来解决
本地搭建服务器应用,在局域网内可以访问,但在外网不能访问。如何实现外网访问内网ip?主要有两种方案:路由器端口映射和快解析内网映射。根据自己本地网络环境,结合是否有公网IP,是否有路由权限,…...

[acwing周赛复盘] 第 91 场周赛20230218
[acwing周赛复盘] 第 91 场周赛20230218 一、本周周赛总结二、 4861. 构造数列1. 题目描述2. 思路分析3. 代码实现三、4862. 浇花1. 题目描述2. 思路分析3. 代码实现四、4863. 构造新矩阵1. 题目描述2. 思路分析3. 代码实现六、参考链接一、本周周赛总结 这周挺难的。T1 贪心分…...

蓝桥12届
小蓝准备用 256MB 的内存空间开一个数组,数组的每个元素都是 32 位 二进制整数,如果不考虑程序占用的空间和维护内存需要的辅助空间,请问 256MB 的空间可以存储多少个 32 位二进制整数?1MB 1024KB 1KB 1024字节(byte) 1字节 8位…...
)
华为OD机试 - 斗地主(JS)
斗地主 题目 斗地主起源于湖北十堰房县, 据传是一位叫吴修全的年轻人根据当地流行的扑克玩法“跑得快”改编的, 如今已风靡整个中国,并流行于互联网上 牌型: 单顺,又称顺子,最少5张牌,最多12张牌(3...A),不能有2, 也不能有大小王,不计花色 例如:3-4-5-7-8,7-8-9-1…...

【MyBatis】| MyBatis的注解式开发
目录 一:MyBatis的注解式开发 1. Insert注解 2. Delete注解 3. Update注解 4. Select注解 5. Results注解 一:MyBatis的注解式开发 MyBatis中也提供了注解式开发⽅式,采⽤注解可以减少Sql映射⽂件的配置。 当然,使⽤注…...
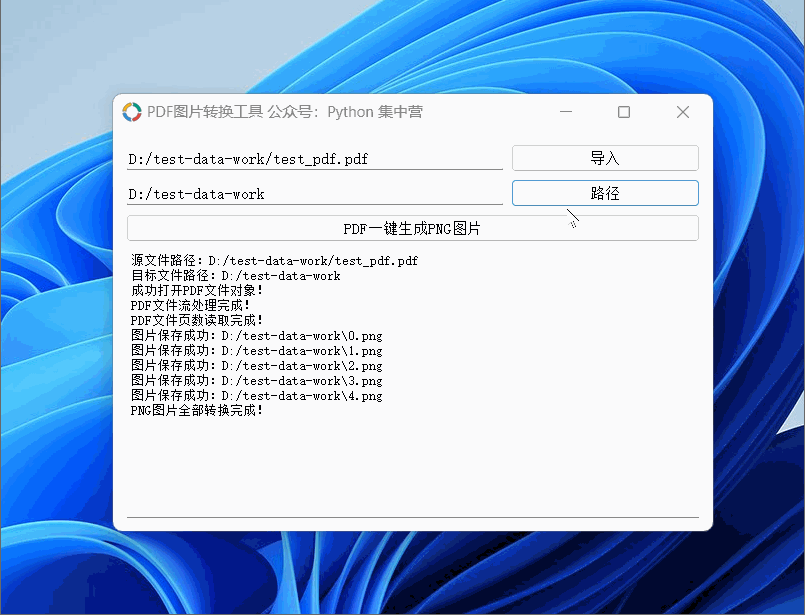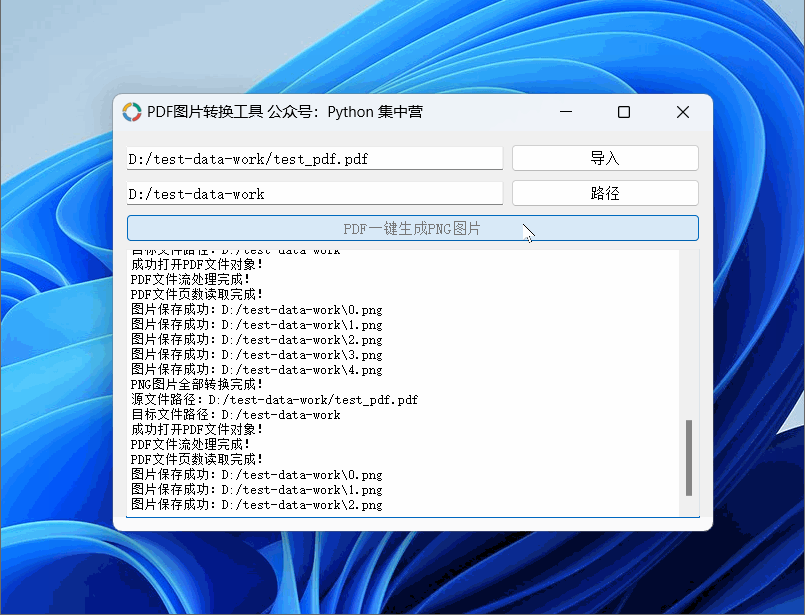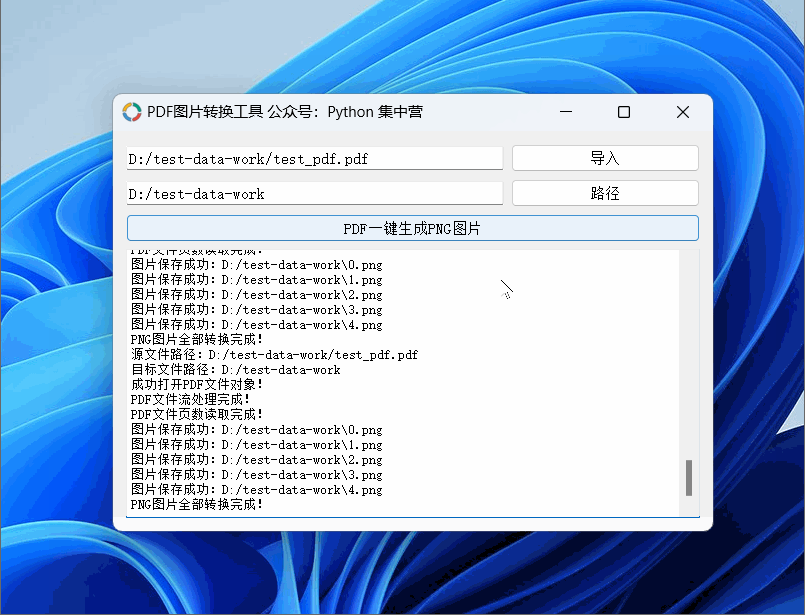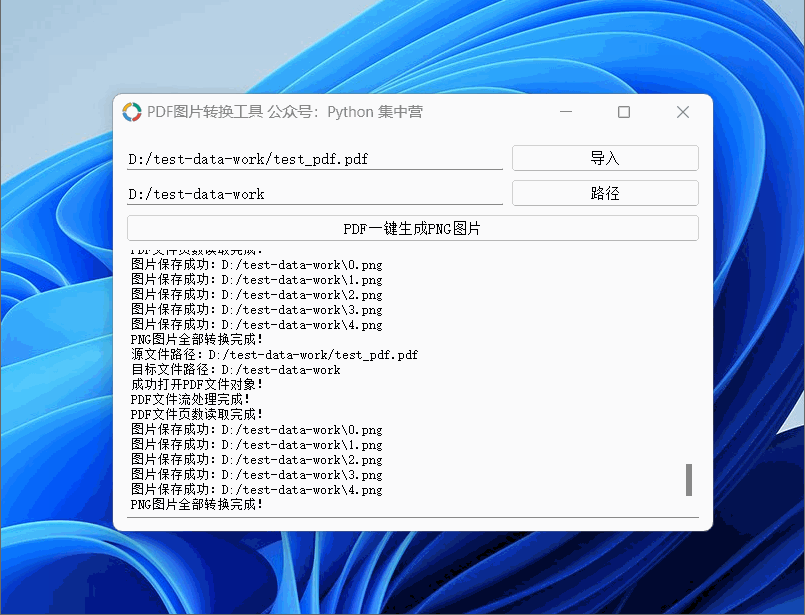
python自制PDF转换.PNG格式图片(按每页生成图片完整源码)小工具!
使用PyQt5应用程序制作PDF转换成图片的小工具,可以导入PDF文档后一键生成对应的PNG图片。 PDF图片转换小工具使用的中间件: python版本:3.6.8 UI应用版本:PyQt5 PDF文件操作非标准库:PyPDF2 PNG图片生成库࿱…...

Go 数组和切片反思
切片的底层数据结构是数组,所以,切片是基于数组的上层封装,使用数组的场景,也完全可以使用切片。 类型比较 我看到 go 1.17 有对切片和数组转换的优化,禁不住纳闷,有什么场景是必须数组来完成的呢&#x…...
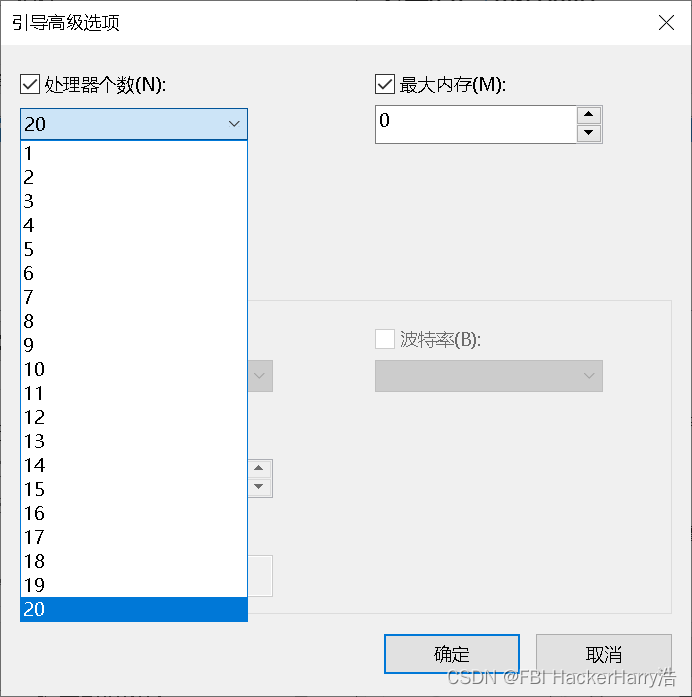
win10电脑性能优化设置
win10电脑性能优化设置 目录win10电脑性能优化设置1.桌面图标显示2.wini2.1 “系统”2.1.1专注助手 关2.1.2 电源和睡眠 设置为从不2.1.3 存储 开2.2 网络和Internet2.3 个性化2.4 应用2.5 账户2.6 游戏2.7 隐私墨迹书写和键入个性化:关活动历史记录:全部…...

作为初学者必须要了解的几种常用数据库!
现在已经存在了很多优秀的商业数据库,如甲骨文(Oracle)公司的 Oracle 数据库、IBM 公司的 DB2 数据库、微软公司的 SQL Server 数据库和 Access 数据库。同时,还有很多优秀的开源数据库,如 MySQL 数据库,Po…...

小红书日常实习一面面经
时间:2月13下午 平台:赛码网,视频面大概70分钟顺序大致是下面,讲到哪问到哪,基础知识最好要结合项目或者实际回答,没录音不完全,有错误请指正首先面试官人超级好,细心提问,耐心解答问…...
)
将Nginx 核心知识点扒了个底朝天(一)
什么是Nginx? Nginx是一个 轻量级/高性能的反向代理Web服务器,用于 HTTP、HTTPS、SMTP、POP3 和 IMAP 协议。他实现非常高效的反向代理、负载平衡,他可以处理2-3万并发连接数,官方监测能支持5万并发,现在中国使用ngin…...

SSM项目搭建保姆级教程
文章目录1、什么是SSM框架1.1、持久层1.2、业务层1.3、表现层1.4、View层1.5、SpringMVC执行流程1.6、MyBatis2、SSM实战搭建2.1、创建工程2.2、添加依赖2.3、配置spring.xml文件2.4、配置web.xml文件2.5、log4j.properties2.6、准备表2.7、实体类2.8、mapper2.9、service2.10、…...

LeetCode 350. 两个数组的交集 II
原题链接 难度:easy\color{Green}{easy}easy 题目描述 给你两个整数数组 nums1nums1nums1 和 nums2nums2nums2 ,请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数,应与元素在两个数组中都出现的次数一致(如果出现…...

Python可以解码吗,解码打码是如何实现的
前言 咳咳,进来的铁汁都是抱着学习的心态进来看的吧,咱今天不讲解解码,咱来说说python如何来实现打码功能~ 这一个个进来的 都是标题党吧哈哈哈 有兴趣的可以继续看看哦 最近重温了一档综艺节目 至于叫什么 这里就不细说了 老是看着看着就…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
