微分流形学习之一:基本定义
微分流形学习之一:基本定义引入
- 引言
- 一、微分流形的历史简介
- 二、拓扑空间
- 三、微分流形
引言
本文是作者在学习微分流形的时候的笔记,尽量严格完整,并带有一定理解,绝不是结论的简单罗列。如果读者知道数学分析中的 ϵ − δ \epsilon-\delta ϵ−δ 语言,将会是有益的。由于本人学识有限,如有不足之处,还请各位专家批评指正。
一、微分流形的历史简介
几何学是一门古老的学科,早在古希腊时期就已经自成体系,欧几里德的公理化著作《几何原本》(约公元前300年写成)更是成为传世佳作而为后人吸取其中的养分。直到17世纪,笛卡尔提出了笛卡尔坐标系,开创了解析几何的先河。随着19世纪的到来,几何学进入了黄金时代。这一时期几何学发生了巨大变化,并向欧式几何发起了挑战,逐渐形成了非欧几何。而“黎曼式的非欧几何”——黎曼几何则对几何学观念进行了全面革新。
值得指出的是,“黎曼式非欧几何”严格来说并不能完全概括黎曼几何,正如胡作玄先生在《近代数学史》中指出的,“黎曼不仅仅提出黎曼式的非欧几何,同时发展了高斯的曲面论,创立了内蕴几何学,以流形为研究对象,从此几何学由图形的研究转变为队空间的研究,而且这空间不再局限于现实的三维空间,而成为任意维度的,这导致后期的高维几何学的发展。”
二、拓扑空间
我们知道,一个定义在拓扑空间上的函数(映射)是可以讨论连续性的,而连续性是分析数学的基础也是后面将要讲到的微分流形的基础,因此我们先来看一下拓扑空间的定义。
定义 一个集合 X X X 的幂集为其所有子集构成之全体,记作 P ( X ) \mathscr{P}(X) P(X) 或 2 X 2^X 2X,本文以 P ( X ) \mathscr{P}(X) P(X) 为准。
例如 X = { a , b } X=\{ a, b \} X={a,b} ,那么 P ( X ) = { ∅ , { a } , { b } , { a , b } } \mathscr{P}(X)=\{ \varnothing, \{a\}, \{b\}, \{a,b\} \} P(X)={∅,{a},{b},{a,b}} 。
值得一提的是,全文涉及的集合 X X X 可以是集合论范畴里面讨论的非常一般的没有特殊指代的形式化的集合,而不仅仅是像数集 R n \mathbb{R}^n Rn 这样一类特殊的集合。
定义 给定集合 X X X 和它的一个子集族 T \mathscr{T} T ,如果 T \mathscr{T} T 满足下述三个条件 1 1 1- 3 3 3,则称 T \mathscr{T} T 为 X X X 上的一个拓扑, T \mathscr{T} T 中的每个集合元素称为 X X X 的开集,并将 ( X , T ) (X,\mathscr{T}) (X,T) 称为拓扑空间。
- ∅ ∈ T , X ∈ T \varnothing \in \mathscr{T}, \; X \in \mathscr{T} ∅∈T,X∈T
- 若 U 1 , U 2 ∈ T U_1, U_2 \in \mathscr{T} U1,U2∈T,则 U 1 ∩ U 2 ∈ T U_1 \cap U_2 \in \mathscr{T} U1∩U2∈T
- 设 Λ \Lambda Λ 为指标集,如果集族 { U λ ∣ λ ∈ Λ } ⊆ T \{ U_{\lambda} | \lambda \in \Lambda \} \subseteq \mathscr{T} {Uλ∣λ∈Λ}⊆T 那么 ⋃ λ ∈ Λ U λ ∈ T \bigcup _{\lambda \in \Lambda} U_{\lambda} \in \mathscr{T} ⋃λ∈ΛUλ∈T
由定义知,拓扑空间是一个全集 X X X ,与它的某些满足上述规则的子集构成的子集族 T \mathscr{T} T 所共同刻画的。拓扑 T \mathscr{T} T 的开集满足有限交运算和任意并运算的封闭性。如此定义,之于初学者而言,势必有些抽象,我们可以举几个例子。
比如取 X = R X=\mathbb{R} X=R ,则实数集的拓扑为:
T = { G ⊆ R ∣ G = ∪ k ≥ 1 ( a k , b k ) , − ∞ ≤ a k < b k ≤ + ∞ ; ( a i , b i ) ∩ ( a j , b j ) = ∅ 如果 i ≠ j } ⋃ { ∅ } \mathscr{T} = \{ G \subseteq R \;|\; G = \cup_{k\geq 1} (a_k, b_k) , \; -\infty \leq a_k<b_k \leq +\infty ; \\ (a_i, b_i) \cap (a_j, b_j) = \varnothing \text{ 如果 } i \neq j \} \bigcup \{ \varnothing \} T={G⊆R∣G=∪k≥1(ak,bk),−∞≤ak<bk≤+∞;(ai,bi)∩(aj,bj)=∅ 如果 i=j}⋃{∅} 即 R \mathbb{R} R 中的开集,除了空集外,其余非空开集都是可数个(含有限个)互不相交的开区间的并。这也是 R \mathbb{R} R 上的通常拓扑,我们还可以在其上赋予其它类型的拓扑,比如平凡拓扑、离散拓扑、下限拓扑(Sorgenfrey 直线)等等。而数学分析里面讨论函数极限、连续等所涉及的拓扑则是 R \mathbb{R} R 的通常拓扑。下面来看看平凡拓扑、离散拓扑的定义。
定义 我们将 ( X , T ) (X, \mathscr{T}) (X,T) 称为平凡拓扑空间,如果 T = { ∅ , X } \mathscr{T}=\{ \varnothing, X \} T={∅,X} 。
定义 我们将 ( X , T ) (X, \mathscr{T}) (X,T) 称为离散拓扑空间,如果 T = P ( X ) \mathscr{T}=\mathscr{P}(X) T=P(X) 。
易验证,上面两个定义中的集族 T \mathscr{T} T 皆满足拓扑空间之定义,不再赘述。如果我们将开集的补集称为闭集,那么闭集满足的性质 2 2 2- 3 3 3 正好跟开集的反过来,即闭集满足有限并和任意交的封闭性。容易发现,平凡拓扑和离散拓扑的任何开集也同样是闭集,这是其它拓扑所不具备的性质。平凡拓扑因包含元素最少,我们也可以称之为集合 X X X 上的最粗拓扑,而离散拓扑包含的元素最多,也被称为 X X X 上的最细拓扑。
除了方便讨论函数的连续性外,拓扑空间自身还有许多重要的性质。比如流形定义中所要涉及的 Hausdorff 性质(也被称为 T2 分离性)。引入 Hausdorff 性质也是为了研究拓扑空间的可度量性,因为 Hausdorff 性质是可度量性的必要条件。我们将满足 Hausdorff 性质的拓扑空间称为 Hausdorff 空间,如果一个拓扑空间不是 Hausdorff 空间,那么该空间一定是不可度量的,即该空间不存在一个二元函数 ρ ( x , y ) \rho(x, y) ρ(x,y),同时满足正定、对称和三角不等式三个性质。为了保证流形具有较好的性质,我们往往要加上这个硬性条件,定义如下:
定义 如果拓扑空间 ( X , T ) (X, \mathscr{T}) (X,T) 满足对于 ∀ x , y ∈ X \forall x, y \in X ∀x,y∈X, x ≠ y x\neq y x=y,存在包含 x x x 的开集 U x U_x Ux 与包含 y y y 的开集 U y U_y Uy,使得 U x ∩ U y = ∅ U_x \cap U_y = \varnothing Ux∩Uy=∅,则称 X X X 是 Hausdorff 的, ( X , T ) (X, \mathscr{T}) (X,T) 为 Hausdorff 空间。
Hausdorff 性质保证了集合 X X X 里的任意两个元素 x , y x,y x,y 在 X X X 的拓扑中是可以区分开的。我们来看几个 Hausdorff 空间的例子。
例如实数集 R \mathbb{R} R 上面配备了通常拓扑,则该拓扑空间是 Hausdorff 空间。这是因为,任意两个包含 x x x 和 y y y 的且不相交的开区间可以由下式来构造:
U x = ( x − y − x 2 , x + y − x 2 ) , U_x = \left (x-\frac{y-x}{2}, x+\frac{y-x}{2} \right) , Ux=(x−2y−x,x+2y−x), U y = ( y − y − x 2 , y + y − x 2 ) . U_y = \left (y-\frac{y-x}{2}, y+\frac{y-x}{2} \right) . Uy=(y−2y−x,y+2y−x). 为了快速过度到微分流形的概念上,我们最后引入拓扑空间同胚的概念,这也是拓扑学里最非常重要的概念之一。为此我们先给出拓扑空间连续函映射的定义。
定义 给定 ( X , T X ) (X, \mathscr{T}_X) (X,TX) 和 ( Y , T Y ) (Y, \mathscr{T}_Y) (Y,TY) 两个拓扑空间,称映射 f : X → Y f: X \rightarrow Y f:X→Y 是连续的,如果对于 Y Y Y 中任意的开集 U ∈ T Y U \in \mathscr{T}_Y U∈TY,其在 f f f 下的原像 f − 1 ( U ) f^{-1}(U) f−1(U) 是 X X X 中的一个开集,即 f − 1 ( U ) ∈ T X f^{-1}(U) \in \mathscr{T}_X f−1(U)∈TX。
值得注意的是,给定的拓扑不同,同样的函数 f f f 可能具有连续或不连续等不同性质。现在考虑实数集上的通常拓扑 T \mathscr{T} T,取 ( X , T X ) = ( R , T ) (X, \mathscr{T}_X)=(\mathbb{R}, \mathscr{T}) (X,TX)=(R,T), ( Y , T Y ) = ( R , T ) (Y, \mathscr{T}_Y)=(\mathbb{R}, \mathscr{T}) (Y,TY)=(R,T),记 f ( x ) = x f(x)=x f(x)=x,则 f f f 显然是 X → Y X\rightarrow Y X→Y 的连续映射,因为 Y = R Y=\mathbb{R} Y=R , f f f 也被称为连续函数。事实上,对于任意的 R \mathbb{R} R 中的开集 G = ∪ k ≥ 1 ( a k , b k ) G = \cup_{k\geq 1} (a_k, b_k) G=∪k≥1(ak,bk),则 f − 1 ( G ) = ∪ k ≥ 1 f − 1 ( ( a k , b k ) ) = ∪ k ≥ 1 ( a k , b k ) = G f^{-1}(G)=\cup_{k\geq 1}f^{-1}((a_k, b_k))=\cup_{k\geq 1} (a_k, b_k)=G f−1(G)=∪k≥1f−1((ak,bk))=∪k≥1(ak,bk)=G 为开集(由恒等映射可直接得出 f − 1 ( G ) = G f^{-1}(G)=G f−1(G)=G,此处为了强调一般的计算过程,所以将中间两步给予保留)。
这也是一个拓扑味道很浓的连续性的定义,这样定义的连续性才具有更广泛的适用性。事实上,我们通过数学分析方式证明的 f ( x ) = x f(x)=x f(x)=x 的连续性与上面通过拓扑方式证明的连续性,在本质上是一致的,但数学分析为何不沿用拓扑的方式来定义连续性呢?主要是我们在数学分析当中涉及的空间 R n \mathbb{R}^n Rn 其自身是具备更多更好的性质的,比如 R n \mathbb{R}^n Rn 可以度量化,即具有通常的距离:
ρ = ∥ x − y ∥ = ( x 1 − y 1 ) 2 + ⋯ + ( x n − y n ) 2 \rho =\| x-y \|=\sqrt{(x_1-y_1)^2+\cdots + (x_n-y_n)^2} ρ=∥x−y∥=(x1−y1)2+⋯+(xn−yn)2 因此,我们可以通过距离的方式来刻画函数的极限与连续性,而且也很直观。只有拓扑方式的连续性定义才能将函数的连续性推广到不可度量的拓扑空间中,并带来更统一的观点。
我们再来考虑实数集上的平凡拓扑 T 1 \mathscr{T}_1 T1 和通常拓扑 T \mathscr{T} T,取 ( X , T X ) = ( R , T 1 ) (X, \mathscr{T}_X)=(\mathbb{R}, \mathscr{T}_1) (X,TX)=(R,T1), ( Y , T Y ) = ( R , T ) (Y, \mathscr{T}_Y)=(\mathbb{R}, \mathscr{T}) (Y,TY)=(R,T),记 f ( x ) = x f(x)=x f(x)=x,则 f : X → Y f: X \rightarrow Y f:X→Y 是不连续的,因为 f − 1 ( ( 0 , 1 ) ) = ( 0 , 1 ) f^{-1}((0, 1))=(0, 1) f−1((0,1))=(0,1) 不是 ( R , T 1 ) (\mathbb{R}, \mathscr{T}_1) (R,T1) 的开集(其开集仅 ∅ \varnothing ∅ 和 R \mathbb{R} R 两个)。
综上,我们知道连续性跟拓扑是有很大关系的,同一个函数,如果更换了拓扑,那么它的连续性质就可能会改变。接下来可以给出同胚的概念了。
定义 设 ( X , T X ) (X, \mathscr{T}_X) (X,TX) 和 ( Y , T Y ) (Y, \mathscr{T}_Y) (Y,TY) 是两个拓扑空间,映射 f : X → Y f: X \rightarrow Y f:X→Y 若满足下述三个性质:
- f f f 是一个双射,
- f f f 是连续的,
- f − 1 f^{-1} f−1 是连续的,
则称 f f f 为这两个拓扑空间的同胚映射(homeomorphism),而称 ( X , T X ) (X, \mathscr{T}_X) (X,TX) 和 ( Y , T Y ) (Y, \mathscr{T}_Y) (Y,TY) 是同胚的(homeomorphic),记作 X ≅ Y X \cong Y X≅Y。
由定义知,同胚是一个等价关系,即满足自反、对称和传递性。同胚的性质告诉我们,哪些拓扑空间是同一类,哪些又是不同类的。而同胚的两个拓扑空间,在拓扑意义下是完全相同的,具有一样的拓扑性质。
比如赋予通常拓扑的实数集构成的拓扑空间 ( R , T ) (\mathbb{R}, \mathscr{T}) (R,T),与 R \mathbb{R} R 的开区间诱导的子拓扑空间 ( ( a , b ) , T ∣ ( a , b ) ) ((a,b), \mathscr{T}|_{(a,b)}) ((a,b),T∣(a,b)) 是同胚的。下面给出分析化的证明,“诱导的子拓扑空间”将在证明之后给出定义。
令 f ( x ) = a e − x + b e x e − x + e x f(x)=\frac{a e^{-x}+be^x}{e^{-x} + e^{x}} f(x)=e−x+exae−x+bex ,则 f ( x ) f(x) f(x) 是一个单射,用反证法说明,设有两个数 x , y ∈ R x, y \in \mathbb{R} x,y∈R 使得 f ( x ) = f ( y ) f(x)=f(y) f(x)=f(y),可得 ( a + b e 2 x ) ( 1 + e 2 y ) = ( a + b e 2 y ) ( 1 + e 2 x ) (a+be^{2x})(1+e^{2y})=(a+be^{2y})(1+e^{2x}) (a+be2x)(1+e2y)=(a+be2y)(1+e2x) ,化简得到 a ( e 2 y − e 2 x ) = b ( e 2 y − e 2 x ) a(e^{2y}-e^{2x})=b(e^{2y}-e^{2x}) a(e2y−e2x)=b(e2y−e2x),由于 a < b a<b a<b,可得 x = y x=y x=y。
我们说明 f ( x ) f(x) f(x) 也是一个满射,任取 y ∈ ( a , b ) y \in (a,b) y∈(a,b),如果存在 x ∈ R x \in \mathbb{R} x∈R 使得 f ( x ) = y f(x) = y f(x)=y,则 a + b e 2 x = y + y e 2 x a+be^{2x}=y+ye^{2x} a+be2x=y+ye2x,进一步解得:
x = ln ( y − a ) − ln ( b − y ) 2 x = \frac{\ln(y-a) - \ln(b-y)}{2} x=2ln(y−a)−ln(b−y) 因此 f ( x ) f(x) f(x) 是满射,从而 f f f 是 R → ( a , b ) \mathbb{R}\rightarrow (a,b) R→(a,b) 的双射。根据数学分析知, f ( x ) f(x) f(x) 是一个初等函数,因此在其定义域区间内是连续的。反过来,易知
f − 1 ( x ) = 1 2 ln ( x − a b − x ) f^{-1}(x) = \frac{1}{2}\ln \left(\frac{x-a}{b-x} \right) f−1(x)=21ln(b−xx−a) 其在 ( a , b ) (a, b) (a,b) 上显然是连续的。
综合上述讨论,在 R \mathbb{R} R 的通常拓扑 T \mathscr{T} T 下, R \mathbb{R} R 和 ( a , b ) (a, b) (a,b) 是同胚的,其中 ( a , b ) (a,b) (a,b) 的拓扑为由 T \mathscr{T} T 所诱导。
定义 设 ( X , T ) (X,\mathscr{T}) (X,T) 为拓扑空间, Y ⊆ X Y\subseteq X Y⊆X 为非空子集,记
T ∣ Y = { Y ∩ U ∣ U ∈ T } \mathscr{T}|_{Y}=\{ Y\cap U| \; U \in \mathscr{T} \} T∣Y={Y∩U∣U∈T} 为 Y Y Y 的子集族,则 T ∣ Y \mathscr{T}|_{Y} T∣Y 为 Y Y Y 上的一个拓扑,称为由 T \mathscr{T} T 诱导的拓扑或子拓扑, ( Y , T ∣ Y ) (Y, \mathscr{T}|_{Y}) (Y,T∣Y) 称为 ( X , T ) (X, \mathscr{T}) (X,T) 的诱导拓扑空间或子拓扑空间。
可以说子拓扑空间自然地继承了原拓扑空间的很多性质,方便讨论某些具体情形。
由以上讨论知, ( R , T ) (\mathbb{R}, \mathscr{T}) (R,T) 和 ( ( a , b ) , T ∣ ( a , b ) ) ((a,b), \mathscr{T}|_{(a,b)}) ((a,b),T∣(a,b)) 是同胚的,因此它们两者在拓扑意义下是没有任何区别的。我们可以理解为区间 ( a , b ) (a,b) (a,b) 可以经过连续形变最后拉伸成 R \mathbb{R} R;实值线 R \mathbb{R} R 也可以连续压缩成 ( a , b ) (a,b) (a,b) ,其实我们讨论的对象一直没有实质改变。若要问实质改变是怎样的,我们也可以拿一把剪刀,将区间 ( a , b ) (a,b) (a,b) 剪断,那么这样的操作就不再是连续变化的,而是瞬间给出了明显的改变,这样得到的两个区间 ( a , r ) (a, r) (a,r) 和 ( r , c ) (r, c) (r,c),其并集 ( a , r ) ∪ ( r , c ) (a, r) \cup (r, c) (a,r)∪(r,c) 将不再与 R \mathbb{R} R 同胚了。是因为剪掉之后的并集 ( a , r ) ∪ ( r , c ) (a, r) \cup (r, c) (a,r)∪(r,c) 不连通,而 R \mathbb{R} R 是连通的,且连通性是拓扑不变量,故两者一定不同胚(同胚的两个拓扑空间其拓扑不变量也必须是相同的)。
有读者可能会问,为什么剪断之后的区间是 ( a , r ) (a, r) (a,r) 和 ( r , c ) (r, c) (r,c),而不是别的其他情况,比如 ( a , r ] (a, r] (a,r] 和 ( r , b ) (r,b) (r,b) ?这是因为考虑到实际生活中,剪开的纸带是不能再拼回去的,所以就将中间的数字 r r r 也一并剪掉。
同胚可能还可以通过构造相关函数来判断,但不同胚怎样判断呢?我们肯定不可能通过构造去逐个说明函数 f f f 不满足同胚的定义,如前所述,正确的方法就是去探寻拓扑空间的不变量,通过不变量的不一致来反推两拓扑空间的不同胚。由于拓扑不变量贯穿拓扑学的始终,内容繁多,遂不在此处详细论述了。
有了以上基础,我们可以引入微分流形的定义了。
三、微分流形
令 ( M , M ) (M, \mathscr{M}) (M,M) 是一个 Hausdorff 拓扑空间,设 f : M → R f: M \rightarrow \mathbb{R} f:M→R 为 M M M 到 R \mathbb{R} R 的实值函数,在定义微分流形之前,先来看看这个问题:如何讨论 f f f 在 M M M 上的导数呢?我们知道,仅仅通过拓扑空间的框架是无法实现求导的。
注意到导数是局部定义的,比如我们可以取 f ( x , y ) = ∣ x ⋅ y ∣ f(x, y)=|x\cdot y| f(x,y)=∣x⋅y∣ 是定义在单位圆周 M = { ( x , y ) ∣ x = cos ( θ ) , y = sin ( θ ) , 0 ≤ θ < 2 π } M = \{ (x,y) | \; x=\cos(\theta), y=\sin(\theta), 0\leq \theta < 2\pi \} M={(x,y)∣x=cos(θ),y=sin(θ),0≤θ<2π} 上的二元连续函数,那么如何考虑 f ( x , y ) f(x,y) f(x,y) 在单位圆周 M M M 上的导数呢?
不妨固定单位圆上的一个点 ( x 0 , y 0 ) = ( 0 , 1 ) (x_0, y_0) = (0, 1) (x0,y0)=(0,1),记单位圆周上动点 ( x , y ) (x,y) (x,y) 到 ( 0 , 1 ) (0,1) (0,1) 的小弧线距离为 l ( x , y ) ( 0 , 1 ) ⌢ > 0 l_{\overset{\frown}{(x,y) (0,1)}} >0 l(x,y)(0,1)⌢>0,则:
∂ f ( x , y ) ∂ M ∣ ( 0 , 1 ) = lim ( x , y ) → ( 0 , 1 ) f ( x , y ) − f ( 0 , 1 ) l ( x , y ) ( 0 , 1 ) ⌢ = lim ( x , y ) → ( 0 , 1 ) f ( x , y ) − f ( 0 , 1 ) x 2 + ( y − 1 ) 2 = lim θ → π / 2 ∣ sin ( θ ) cos ( θ ) ∣ cos 2 ( θ ) + ( sin ( θ ) − 1 ) 2 = lim θ → π / 2 sin ( θ ) 1 + sin ( θ ) 2 = 1 \begin{align} \frac{\partial f(x,y)}{\partial M} \bigg|_{(0,1)} &= \lim_{(x,y)\rightarrow (0,1)} \frac{f(x,y)-f(0,1)}{l_{\overset{\frown}{(x,y) (0,1)}}} \\ &= \lim_{(x,y)\rightarrow (0,1)} \frac{f(x,y)-f(0,1)}{\sqrt{x^2+(y-1)^2}} \\ &=\lim_{\theta\rightarrow \pi/2} \frac{|\sin(\theta)\cos(\theta)|}{\sqrt{\cos^2(\theta)+(\sin(\theta)-1)^2}} \\ &= \lim_{\theta\rightarrow \pi/2} \frac{\sin(\theta)\sqrt{1+\sin(\theta)}}{\sqrt{2}} \\ &=1 \end{align} ∂M∂f(x,y) (0,1)=(x,y)→(0,1)liml(x,y)(0,1)⌢f(x,y)−f(0,1)=(x,y)→(0,1)limx2+(y−1)2f(x,y)−f(0,1)=θ→π/2limcos2(θ)+(sin(θ)−1)2∣sin(θ)cos(θ)∣=θ→π/2lim2sin(θ)1+sin(θ)=1 其中, ∂ M \partial M ∂M 表示沿着曲线 M M M 的方向求偏导。在求导过程中,我们做了参数变换,并且涉及 M M M 上 ( 0 , 1 ) (0,1) (0,1) 点的邻域 U ( 0 , 1 ) U_{(0,1)} U(0,1)(即包含 ( 0 , 1 ) (0,1) (0,1) 点的 M M M 中的开集)。由子拓扑的定义,该邻域 U ( 0 , 1 ) U_{(0,1)} U(0,1) 可以表示为 M ∩ D ( 0 , 1 ) M\cap D_{(0,1)} M∩D(0,1),其中 D ( 0 , 1 ) D_{(0,1)} D(0,1) 为 R 2 \mathbb{R}^2 R2 中以 ( 0 , 1 ) (0,1) (0,1) 为圆心的任何一个充分小的开圆盘(不包含圆周的圆盘)。
重要的是,通过参数变换,我们能将邻域 U ( 0 , 1 ) U_{(0,1)} U(0,1) 映射成 R \mathbb{R} R 中的开区间 I I I,而且 U ( 0 , 1 ) ≅ I U_{(0,1)} \cong I U(0,1)≅I。即存在 ϕ : θ ↦ ( cos ( θ ) , sin ( θ ) ) \phi: \theta \mapsto (\cos(\theta), \sin(\theta)) ϕ:θ↦(cos(θ),sin(θ)),将开区间 ( π 2 − ϵ , π 2 + ϵ ) (\frac{\pi}{2}-\epsilon, \frac{\pi}{2}+\epsilon) (2π−ϵ,2π+ϵ) 映射到从点 ( cos ( π 2 − ϵ ) , sin ( π 2 − ϵ ) ) (\cos(\frac{\pi}{2}-\epsilon), \sin(\frac{\pi}{2}-\epsilon)) (cos(2π−ϵ),sin(2π−ϵ)) 到点 ( cos ( π 2 + ϵ ) , sin ( π 2 + ϵ ) ) (\cos(\frac{\pi}{2}+\epsilon), \sin(\frac{\pi}{2}+\epsilon)) (cos(2π+ϵ),sin(2π+ϵ)) 的单位圆的弧线部分 U ( 0 , 1 ) U_{(0,1)} U(0,1)。显然映射 ϕ \phi ϕ 是一双射,而且由 ϵ − δ \epsilon-\delta ϵ−δ 语言明显可证 ϕ ( θ ) \phi(\theta) ϕ(θ) 也是连续的。
对于 ϕ − 1 \phi^{-1} ϕ−1,计算可得 ϕ − 1 ( x , y ) = arccos ( x ) \phi^{-1}(x,y)=\arccos(x) ϕ−1(x,y)=arccos(x),其中 x x x 的取值范围为开区间 ( cos ( π 2 + ϵ ) , cos ( π 2 − ϵ ) ) (\cos(\frac{\pi}{2}+\epsilon), \cos(\frac{\pi}{2}-\epsilon)) (cos(2π+ϵ),cos(2π−ϵ)),同样由 ϵ − δ \epsilon-\delta ϵ−δ 语言可得 ϕ − 1 ( x , y ) \phi^{-1}(x,y) ϕ−1(x,y) 的连续性。
因此,我们得到 U ( 0 , 1 ) ≅ ( π 2 − ϵ , π 2 + ϵ ) ⊆ R U_{(0,1)} \cong (\frac{\pi}{2}-\epsilon, \frac{\pi}{2}+\epsilon) \subseteq \mathbb{R} U(0,1)≅(2π−ϵ,2π+ϵ)⊆R。同胚的好处就在于,我们可以将定义在弯曲图形单位圆 M M M 上某点不知如何求导的函数 f ( x , y ) f(x,y) f(x,y) 拉回到了一个定义在平直的开区间上可以求导的一元函数 f ( θ ) f(\theta) f(θ)。那么我们可以将这个思路进行简单推广。
也即先找到在点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0) 处的单位圆 M M M 中的开邻域 U ( x 0 , y 0 ) U_{(x_0,y_0)} U(x0,y0),然后继续找到从 U ( x 0 , y 0 ) U_{(x_0,y_0)} U(x0,y0) 到 R \mathbb{R} R 中一开集的同胚映射 ψ : U ( x 0 , y 0 ) → ψ ( U ( x 0 , y 0 ) ) \psi: U_{(x_0,y_0)} \rightarrow \psi(U_{(x_0,y_0)}) ψ:U(x0,y0)→ψ(U(x0,y0)),则
f ∘ ψ − 1 : ψ ( U ( x 0 , y 0 ) ) → R f \circ \psi^{-1}: \; \psi(U_{(x_0,y_0)})\rightarrow \mathbb{R} f∘ψ−1:ψ(U(x0,y0))→R 成为定义在 R \mathbb{R} R 中开集 ψ ( U ( x 0 , y 0 ) ) \psi(U_{(x_0,y_0)}) ψ(U(x0,y0)) 上的函数,自然能够讨论微分了。我们取 ψ = ϕ − 1 \psi=\phi^{-1} ψ=ϕ−1, ( x 0 , y 0 ) = ( 0 , 1 ) (x_0,y_0)=(0,1) (x0,y0)=(0,1) 则 f ∘ ψ − 1 ( θ ) = ∣ sin ( θ ) cos ( θ ) ∣ f\circ \psi^{-1}(\theta) = |\sin(\theta)\cos(\theta)| f∘ψ−1(θ)=∣sin(θ)cos(θ)∣。其中函数 f ( x , y ) f(x,y) f(x,y) 与 f ∘ ψ − 1 ( θ ) f\circ \psi^{-1}(\theta) f∘ψ−1(θ) 在各自相应的邻域内虽具有相同的值域,但不是相同的函数,因为两者的定义域不同,故不能将 f ∘ ψ − 1 ( θ ) f\circ \psi^{-1}(\theta) f∘ψ−1(θ) 的导数当做就是 f ( x , y ) f(x,y) f(x,y) 的相应方向导数。
基于此,我们可以正确地对 f f f 来求在点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0) 处沿 M M M 的方向导数:
∂ f ( x , y ) ∂ M ∣ ( x 0 , y 0 ) = lim ( x , y ) → ( x 0 , y 0 ) f ( x , y ) − f ( x 0 , y 0 ) l ( x , y ) ( x 0 , y 0 ) ⌢ = lim θ → θ 0 f ∘ ψ − 1 ( θ ) − f ∘ ψ − 1 ( θ 0 ) l ( x , y ) ( x 0 , y 0 ) ⌢ ( θ ) \begin{align} \frac{\partial f(x,y)}{\partial M} \bigg|_{(x_0,y_0)} &= \lim_{(x,y)\rightarrow (x_0,y_0)} \frac{f(x,y)-f(x_0,y_0)}{l_{\overset{\frown}{(x,\;\;\;y) (x_0,y_0)}}} \\ &= \lim_{\theta \rightarrow \theta_0} \frac{f \circ\psi^{-1}(\theta)-f\circ\psi^{-1}(\theta_0)}{l_{\overset{\frown}{(x,\;\;\; y) (x_0,y_0)}}(\theta)} \end{align} ∂M∂f(x,y) (x0,y0)=(x,y)→(x0,y0)liml(x,y)(x0,y0)⌢f(x,y)−f(x0,y0)=θ→θ0liml(x,y)(x0,y0)⌢(θ)f∘ψ−1(θ)−f∘ψ−1(θ0) 结合上面的所有讨论,我们可以给出流形的定义。
定义 设 ( M , M ) (M, \mathscr{M}) (M,M) 是一个 Hausdorff 拓扑空间,若 M M M 的每一个点 p p p 都有一个邻域 U ⊆ M U \subseteq M U⊆M 以及映射 ϕ : U → ϕ ( U ) \phi: U \rightarrow \phi(U) ϕ:U→ϕ(U),使得 ϕ \phi ϕ 是从开集 U U U 到 ϕ ( U ) ⊆ R n \phi(U)\subseteq \mathbb{R}^n ϕ(U)⊆Rn 的同胚,则称 ( M , M ) (M, \mathscr{M}) (M,M)(或 M M M)是一个 n n n 维拓扑流形。
拓扑流形实际上是在每一个局部都跟 R n \mathbb{R}^n Rn 的一个开子集是同胚的。或者说拓扑流形是将 R n \mathbb{R}^n Rn 中不同的碎块部分连续拼接之后得到的结果。因此,在每一个局部,拓扑流形都可以建立相应的 n n n 维局部坐标系。
我们称 ( U , ϕ ) (U, \phi) (U,ϕ) 为流形 M M M 的坐标卡,将 ϕ ( p ) \phi(p) ϕ(p) 称为点 p ∈ U p\in U p∈U 的坐标。拓扑流形并没有规定微分结构,如果要考虑该结构,我们先从外部函数 f : M → R f:M\rightarrow \mathbb{R} f:M→R 来看,结合前文就应该要求 f ∘ ϕ − 1 f\circ \phi^{-1} f∘ϕ−1 可微,若还有坐标卡 ( V , ψ ) (V, \psi) (V,ψ),同样也要要求 f ∘ ψ − 1 f\circ \psi^{-1} f∘ψ−1 可微,问题的关键就在于两者定义域的公共部分 U ∩ V U \cap V U∩V,如何保证 f ∘ ϕ − 1 f\circ \phi^{-1} f∘ϕ−1 和 f ∘ ψ − 1 f\circ \psi^{-1} f∘ψ−1 都在 U ∩ V U \cap V U∩V 上可微呢 ?做法是这样的:
f ∘ ψ − 1 = f ∘ ϕ − 1 ∘ ϕ ∘ ψ − 1 f\circ \psi^{-1} = f\circ\phi^{-1} \circ\ \phi \circ \psi^{-1} f∘ψ−1=f∘ϕ−1∘ ϕ∘ψ−1 由 f ∘ ϕ − 1 f\circ\phi^{-1} f∘ϕ−1 可微,只需要保证 ϕ ∘ ψ − 1 \phi \circ \psi^{-1} ϕ∘ψ−1 可微就能说明 f ∘ ψ − 1 f\circ \psi^{-1} f∘ψ−1 可微。实际上, ϕ ∘ ψ − 1 : ψ ( U ∩ V ) → ϕ ( U ∩ V ) \phi \circ \psi^{-1}: \psi(U\cap V) \rightarrow \phi(U\cap V) ϕ∘ψ−1:ψ(U∩V)→ϕ(U∩V) 是 R n \mathbb{R}^n Rn 中的开集到 R n \mathbb{R}^n Rn 中的开集的向量值函数,其可微性是数学分析里面所讨论过的熟悉对象。至此,我们可以给出微分流形的定义,首先给出 C r C^r Cr 相关的概念。
我们知道向量值函数 ϕ ∘ ψ − 1 ( x ) \phi \circ \psi^{-1}(x) ϕ∘ψ−1(x) 的可微性归结为每个分量函数 ( ϕ ∘ ψ − 1 ) i ( x ) (\phi \circ \psi^{-1})^i(x) (ϕ∘ψ−1)i(x) 的可微性。若 ( ϕ ∘ ψ − 1 ) i ( x 1 , x 2 , ⋯ , x n ) (\phi \circ \psi^{-1})^i(x_1, x_2, \cdots, x_n) (ϕ∘ψ−1)i(x1,x2,⋯,xn) 有连续的 r r r 阶( r ≥ 1 r\geq 1 r≥1)偏导数,则称 ϕ ∘ ψ − 1 \phi \circ \psi^{-1} ϕ∘ψ−1 是 C r C^r Cr 的(这里 1 ≤ i ≤ n 1\leq i \leq n 1≤i≤n,且 r r r 阶偏导是指所有可能的 r r r 阶偏导)。若 ( ϕ ∘ ψ − 1 ) i ( x 1 , x 2 , ⋯ , x n ) (\phi \circ \psi^{-1})^i(x_1, x_2, \cdots, x_n) (ϕ∘ψ−1)i(x1,x2,⋯,xn) 有连续的任意次偏导,则称 ϕ ∘ ψ − 1 \phi \circ \psi^{-1} ϕ∘ψ−1 是光滑的或 C ∞ C^\infty C∞ 的。若 ( ϕ ∘ ψ − 1 ) i ( x 1 , x 2 , ⋯ , x n ) (\phi \circ \psi^{-1})^i(x_1, x_2, \cdots, x_n) (ϕ∘ψ−1)i(x1,x2,⋯,xn) 在每一点的邻域内都能展开成收敛的幂级数,则称 ϕ ∘ ψ − 1 \phi \circ \psi^{-1} ϕ∘ψ−1 是实解析的,或称为 C ω C^{\omega} Cω 的。
进一步,若用 C n \mathbb{C}^n Cn 替换 R n \mathbb{R}^n Rn,并要求 ( ϕ ∘ ψ − 1 ) i ( z 1 , z 2 , ⋯ , z n ) (\phi \circ \psi^{-1})^i(z_1, z_2, \cdots, z_n) (ϕ∘ψ−1)i(z1,z2,⋯,zn) 在每一点的充分小的圆盘内能展开成收敛的幂级数(实际上就是在其特定的定义域内复解析或全纯),则称 ϕ ∘ ψ − 1 \phi \circ \psi^{-1} ϕ∘ψ−1 是复解析的,或称为 C ω C^{\omega} Cω 的。
定义 设 M M M 是一个拓扑流形, ( U , ϕ ) (U, \phi) (U,ϕ) 和 ( V , ψ ) (V, \psi) (V,ψ) 是它的两个坐标卡。若当 U ∩ V ≠ ∅ U \cap V \neq \varnothing U∩V=∅ 时, ϕ ∘ ψ − 1 \phi \circ \psi^{-1} ϕ∘ψ−1 和 ψ ∘ ϕ − 1 \psi \circ \phi^{-1} ψ∘ϕ−1 都是 C r C^r Cr 的(其中 r r r 是正整数,或 ∞ \infty ∞,或 ω \omega ω),则称坐标卡 ( U , ϕ ) (U, \phi) (U,ϕ) 和 ( V , ψ ) (V, \psi) (V,ψ) 是 C r C^r Cr 相关的。
注意,当 U ∩ V = ∅ U \cap V = \varnothing U∩V=∅ 时,规定 ( U , ϕ ) (U, \phi) (U,ϕ) 和 ( V , ψ ) (V, \psi) (V,ψ) 对于任何取值的 r r r 都是 C r C^r Cr 相关的。接下来,我们给出微分结构的定义。
定义 设 M M M 是一个拓扑流形,假定 A = { ( U α , ϕ α ) : α ∈ I } \mathscr{A}=\{ (U_{\alpha}, \phi_{\alpha}) : \alpha \in I \} A={(Uα,ϕα):α∈I} 是 M M M 的坐标卡之集,且满足下面的条件:
- { U α : α ∈ I } \{ U_{\alpha} : \alpha \in I \} {Uα:α∈I} 构成流形 M M M 的一个开覆盖,
- 属于 A \mathscr{A} A 的任意两个坐标卡都是 C r C^r Cr 相关的,
- A \mathscr{A} A 是 C r C^r Cr 极大的,就是若 ( U , ϕ ) (U, \phi) (U,ϕ) 是 M M M 的一个坐标卡,且 ( U , ϕ ) (U, \phi) (U,ϕ) 与 A \mathscr{A} A 中每一个元素都是 C r C^r Cr 相关的,则 ( U , ϕ ) (U, \phi) (U,ϕ) 必属于 A \mathscr{A} A,
则称坐标卡集 A \mathscr{A} A 为流形 M M M 上的一个 C r C^r Cr 微分结构。当 r = ∞ r=\infty r=∞ 时, A \mathscr{A} A 称为 M M M 上的一个光滑结构,当 r = ω r=\omega r=ω 时, A \mathscr{A} A 称为 M M M 上的一个解析结构,当 r = 0 r=0 r=0 时, A \mathscr{A} A 恰为拓扑流形 M M M 上的坐标卡之全体(或称为连续结构),当 r ≥ 1 r\geq 1 r≥1 时, M M M 上的 C r C^r Cr 微分结构 A \mathscr{A} A 只能是 M M M 上的坐标卡集的一个子集。
实际上,我们可以通过上述定义中的条件 1 和条件 2 推出 条件 3,也就是说条件 3 是多余的。思路就是找到 M M M 上的一组坐标卡 { ( U α , ϕ α ) : α ∈ I } \{ (U_{\alpha}, \phi_{\alpha}) : \alpha \in I \} {(Uα,ϕα):α∈I},使得 { U α : α ∈ I } \{ U_{\alpha} : \alpha \in I \} {Uα:α∈I} 构成 M M M 的开覆盖,并且这组坐标卡是 C r C^r Cr 相关的,则在 M M M 上唯一确定了包含 { ( U α , ϕ α ) : α ∈ I } \{ (U_{\alpha}, \phi_{\alpha}) : \alpha \in I \} {(Uα,ϕα):α∈I} 在内的 C r C^r Cr 微分结构。证明细节留给读者完成。加上条件 3 也是为了强调 C r C^r Cr 微分结构的这一重要特征。
定义 设 M M M 是一个 n n n 维拓扑流形,若在 M M M 上指定了一个 C r C^r Cr 微分结构 A \mathscr{A} A,则称 ( M , A ) (M, \mathscr{A}) (M,A) 为一个 n n n 维 C r C^r Cr 微分流形。属于 A \mathscr{A} A 的坐标卡 ( U , ϕ ) (U, \phi) (U,ϕ) 称为该微分流形的容许坐标卡。
当 r = k r=k r=k 时,就得到一个 C k C^k Ck 流形;当 r = ∞ r=\infty r=∞ 时,得到一个光滑流形;当 r = ω r=\omega r=ω 时,得到一个解析流形,根据背景空间是 R n \mathbb{R}^n Rn 或者 C n \mathbb{C}^n Cn 的不同,分别叫做实解析流形和复解析流形(复流形)。
根据 C r C^r Cr 相关性,我们知道,定义在 C r C^r Cr 流形上的函数 f f f 的可微性是与容许坐标卡的选取无关的。这显然由该式可知:
f ∘ ψ − 1 = f ∘ ϕ − 1 ∘ ϕ ∘ ψ − 1 f\circ \psi^{-1} = f\circ\phi^{-1} \circ\ \phi \circ \psi^{-1} f∘ψ−1=f∘ϕ−1∘ ϕ∘ψ−1 f ∘ ψ − 1 f\circ \psi^{-1} f∘ψ−1 与 f ∘ ϕ − 1 f\circ\phi^{-1} f∘ϕ−1 具有相同的 C r C^r Cr 微分性质。下面我们来列举微分流形的一些例子。
例如 R n \mathbb{R}^n Rn 是一个 n n n 维光滑流形。只需取 U = R n U=\mathbb{R}^n U=Rn, ϕ : U → R n \phi: U\rightarrow \mathbb{R}^n ϕ:U→Rn 为恒等映射,则 R n \mathbb{R}^n Rn 上,由 { ( U , ϕ ) } \{ (U, \phi) \} {(U,ϕ)} 生成的光滑结构称为 R n \mathbb{R}^n Rn 的标准光滑结构。
在 R \mathbb{R} R 上我们来定义两个微分结构,首先有 ( R , ϕ ) (\mathbb{R}, \phi) (R,ϕ),其中 ϕ \phi ϕ 是恒等函数,该坐标卡生成 R \mathbb{R} R 的标准光滑结构 A 1 \mathscr{A}_1 A1。另取 ( R , ψ ) (\mathbb{R}, \psi) (R,ψ),其中同胚 ψ \psi ψ 定义为 ψ ( x ) = x 3 \psi(x)=x^3 ψ(x)=x3,该坐标卡生成 R \mathbb{R} R 的标准光滑结构 A 2 \mathscr{A}_2 A2。易知这两个坐标卡是不相容的,是因为 ϕ ∘ ψ − 1 ( x ) = x 3 \phi \circ \psi^{-1}(x)=\sqrt[3]{x} ϕ∘ψ−1(x)=3x 在 x = 0 x=0 x=0 处是不可导的,因此不是 C ∞ C^{\infty} C∞ 相容的,是两个不同的 C r C^r Cr 结构。
比如 n n n 维球面 S n = { x ∈ R n + 1 ∣ ∣ x ∣ = 1 } S^n = \{ x\in \mathbb{R}^{n+1} | |x|=1 \} Sn={x∈Rn+1∣∣x∣=1} 是一个 n n n 维光滑流形。考虑 S n S^n Sn 继承自欧式空间 R n + 1 \mathbb{R}^{n+1} Rn+1 的子拓扑,则相容性考虑球极投影。
取 P = ( 0 , 0 , ⋯ , 1 ) P=(0,0,\cdots, 1) P=(0,0,⋯,1), Q = ( 0 , 0 , ⋯ , − 1 ) Q=(0,0,\cdots,-1) Q=(0,0,⋯,−1) 是北极和南极点, U = S n − P U=S^n - {P} U=Sn−P, V = S n − Q V=S^n-Q V=Sn−Q,任取 x ∈ U x\in U x∈U,球极投影是连接 x x x 和 P P P 的直线与 y n + 1 = 0 y_{n+1}=0 yn+1=0 平面相交的位置。可取投影 ϕ : U → R n = { y ∈ R n + 1 ∣ y n + 1 = 0 } \phi: U\rightarrow \mathbb{R}^n=\{ y\in \mathbb{R}^{n+1} | \; y_{n+1}=0\} ϕ:U→Rn={y∈Rn+1∣yn+1=0}:
ϕ ( x ) = λ x + ( 1 − λ ) P \phi(x)=\lambda x+(1-\lambda)P ϕ(x)=λx+(1−λ)P 满足 0 = y n + 1 = λ x n + 1 + ( 1 − λ ) P n + 1 0=y_{n+1}=\lambda x_{n+1}+(1-\lambda)P_{n+1} 0=yn+1=λxn+1+(1−λ)Pn+1,得到 λ x n + 1 + ( 1 − λ ) = 0 \lambda x_{n+1}+(1-\lambda)=0 λxn+1+(1−λ)=0,故 λ = 1 1 − x n + 1 \lambda=\frac{1}{1-x_{n+1}} λ=1−xn+11,从而球极投影为:
ϕ ( x ) = x 1 − x n + 1 − x n + 1 1 − x n + 1 P \phi(x)=\frac{x}{1-x_{n+1}}-\frac{x_{n+1}}{1-x_{n+1}}P ϕ(x)=1−xn+1x−1−xn+1xn+1P 反之,求 ψ : V → R n \psi: V\rightarrow \mathbb{R}^n ψ:V→Rn 也可类似作出。考虑球极投影:
ψ ( x ) = λ x + ( 1 − λ ) Q \psi(x) = \lambda x + (1-\lambda)Q ψ(x)=λx+(1−λ)Q 由 0 = y n + 1 = λ x n + 1 + ( 1 − λ ) Q n + 1 0=y_{n+1}=\lambda x_{n+1}+(1-\lambda)Q_{n+1} 0=yn+1=λxn+1+(1−λ)Qn+1 得 λ = 1 1 + x n + 1 \lambda=\frac{1}{1+x_{n+1}} λ=1+xn+11,故有
ψ ( x ) = x 1 + x n + 1 + x n + 1 1 + x n + 1 Q \psi(x)=\frac{x}{1+x_{n+1}}+\frac{x_{n+1}}{1+x_{n+1}}Q ψ(x)=1+xn+1x+1+xn+1xn+1Q 显然 ϕ : U → R n \phi:U\rightarrow \mathbb{R}^n ϕ:U→Rn 和 ψ : V → R n \psi:V\rightarrow \mathbb{R}^n ψ:V→Rn 既单且满同时连续。
再考虑逆映射, ϕ − 1 ( y ) : R n → U \phi^{-1}(y): \mathbb{R}^n \rightarrow U ϕ−1(y):Rn→U,显然连接 P P P 和平面 y n + 1 = 0 y_{n+1}=0 yn+1=0 上点 y y y 的直线会穿过球面的一点 x x x,故有 ∣ λ P + ( 1 − λ ) y ∣ 2 = 1 |\lambda P+(1-\lambda)y|^2=1 ∣λP+(1−λ)y∣2=1,化简得
( 1 − λ ) 2 ∑ i = 1 n y i 2 + λ 2 = 1 (1-\lambda)^2 \sum_{i=1}^{n} y_i^2 + \lambda^2=1 (1−λ)2i=1∑nyi2+λ2=1 解得 λ = ∑ i = 1 n y i 2 − 1 1 + ∑ i = 1 n y i 2 \lambda=\frac{\sum_{i=1}^{n} y_i^2-1}{1+\sum_{i=1}^{n} y_i^2} λ=1+∑i=1nyi2∑i=1nyi2−1,故:
ϕ − 1 ( y ) = λ P + ( 1 − λ ) y = 2 1 + ∑ i = 1 n y i 2 y + ∑ i = 1 n y i 2 − 1 1 + ∑ i = 1 n y i 2 P \phi^{-1}(y)=\lambda P+(1-\lambda)y=\frac{2}{1+\sum^{n}_{i=1}y_i^2}y+\frac{\sum_{i=1}^{n} y_i^2-1}{1+\sum_{i=1}^{n} y_i^2}P ϕ−1(y)=λP+(1−λ)y=1+∑i=1nyi22y+1+∑i=1nyi2∑i=1nyi2−1P 同理可得 ψ − 1 ( y ) : R n → V \psi^{-1}(y): \mathbb{R}^n \rightarrow V ψ−1(y):Rn→V:
ψ − 1 ( y ) = λ Q + ( 1 − λ ) y = 2 1 + ∑ i = 1 n y i 2 y + ∑ i = 1 n y i 2 − 1 1 + ∑ i = 1 n y i 2 Q \psi^{-1}(y)=\lambda Q+(1-\lambda)y=\frac{2}{1+\sum^{n}_{i=1}y_i^2}y+\frac{\sum_{i=1}^{n} y_i^2-1}{1+\sum_{i=1}^{n} y_i^2}Q ψ−1(y)=λQ+(1−λ)y=1+∑i=1nyi22y+1+∑i=1nyi2∑i=1nyi2−1Q 因此 ϕ − 1 \phi^{-1} ϕ−1 和 ψ − 1 \psi^{-1} ψ−1 连续,故 ϕ \phi ϕ 和 ψ \psi ψ 系同胚, S n S^n Sn 为拓扑流形。
由于 ϕ ∘ ψ − 1 ( y ) = ϕ ∘ ψ − 1 ∘ ψ ( x ) = ϕ ( x ) \phi\circ \psi^{-1}(y)=\phi\circ \psi^{-1}\circ \psi(x)=\phi(x) ϕ∘ψ−1(y)=ϕ∘ψ−1∘ψ(x)=ϕ(x), y = ψ ( x ) y=\psi(x) y=ψ(x),因此复合映射 ϕ ∘ ψ − 1 ( y ) \phi\circ \psi^{-1}(y) ϕ∘ψ−1(y) 将 ψ ( x ) \psi(x) ψ(x) 映射为 ϕ ( x ) \phi(x) ϕ(x)。
我们记 ∑ i = 1 n y i 2 = ∣ y ∣ 2 \sum^{n}_{i=1}y_i^2=|y|^2 ∑i=1nyi2=∣y∣2,结合上面计算得到的 x n + 1 = 1 − ∣ y ∣ 2 1 + ∣ y ∣ 2 x_{n+1}=\frac{1-|y|^2}{1+|y|^2} xn+1=1+∣y∣21−∣y∣2,代入 ϕ ∘ ψ − 1 ( y ) \phi\circ \psi^{-1}(y) ϕ∘ψ−1(y) 得:
ϕ ∘ ψ − 1 ( y ) = ( 2 1 + ∣ y ∣ 2 y + ∣ y ∣ 2 − 1 1 + ∣ y ∣ 2 Q ) 1 + ∣ y ∣ 2 2 ∣ y ∣ 2 − 1 − ∣ y ∣ 2 2 ∣ y ∣ 2 P = y ∣ y ∣ 2 + ∣ y ∣ 2 − 1 2 ∣ y ∣ 2 Q − 1 − ∣ y ∣ 2 2 ∣ y ∣ 2 P = y ∣ y ∣ 2 \begin{align} & \phi\circ \psi^{-1}(y) \\ &= \left(\frac{2}{1+|y|^2}y+\frac{|y|^2-1}{1+|y|^2}Q \right)\frac{1+|y|^2}{2|y|^2} - \frac{1-|y|^2}{2|y|^2}P \\ &=\frac{y}{|y|^2}+\frac{|y|^2-1}{2|y|^2}Q-\frac{1-|y|^2}{2|y|^2}P \\ &= \frac{y}{|y|^2} \end{align} ϕ∘ψ−1(y)=(1+∣y∣22y+1+∣y∣2∣y∣2−1Q)2∣y∣21+∣y∣2−2∣y∣21−∣y∣2P=∣y∣2y+2∣y∣2∣y∣2−1Q−2∣y∣21−∣y∣2P=∣y∣2y 因此易得 ϕ ∘ ψ − 1 : ψ ( U ∩ V ) = R n \ { 0 } → ϕ ( U ∩ V ) = R n \ { 0 } \phi \circ \psi^{-1}: \psi(U\cap V)=\mathbb{R}^n \backslash \{\bold{0}\} \rightarrow \phi(U\cap V)=\mathbb{R}^n \backslash \{\bold{0}\} ϕ∘ψ−1:ψ(U∩V)=Rn\{0}→ϕ(U∩V)=Rn\{0} 是一个光滑映射。同理易得(此时 x n + 1 = ∣ y ∣ 2 − 1 1 + ∣ y ∣ 2 x_{n+1}=\frac{|y|^2-1}{1+|y|^2} xn+1=1+∣y∣2∣y∣2−1),
ψ ∘ ϕ − 1 ( y ) = 2 y + ( ∣ y ∣ 2 − 1 ) P 2 ∣ y ∣ 2 + ∣ y ∣ 2 − 1 2 ∣ y ∣ 2 Q = y ∣ y ∣ 2 \begin{align} &\psi \circ \phi^{-1}(y) \\ &=\frac{2y+(|y|^2-1)P}{2|y|^2} + \frac{|y|^2-1}{2|y|^2}Q \\ &=\frac{y}{|y|^2} \end{align} ψ∘ϕ−1(y)=2∣y∣22y+(∣y∣2−1)P+2∣y∣2∣y∣2−1Q=∣y∣2y 显然, ψ ∘ ϕ − 1 \psi \circ \phi^{-1} ψ∘ϕ−1 也是一个光滑映射,因此, A = { ( U , ϕ ) , ( V , ψ ) } \mathscr{A}=\{ (U,\phi), (V, \psi) \} A={(U,ϕ),(V,ψ)} 是 C ∞ C^{\infty} C∞ 相容的,确定了 S n S^n Sn 上的一个 C ∞ C^{\infty} C∞ 微分结构,故球面 S n S^{n} Sn 是光滑流形。
另一个不能绕开的例子,则是 n n n 维实射影空间 R P n RP^n RPn。实射影空间是 R n + 1 \mathbb{R}^{n+1} Rn+1 中过原点的一切直线之集,也可以说是 R n + 1 \mathbb{R}^{n+1} Rn+1 中全体一维线性子空间组成的集合。
在 R n + 1 \ { 0 } \mathbb{R}^{n+1}\backslash \{ \bold{0} \} Rn+1\{0} 中,记 x ∼ y x \sim y x∼y 为存在非零实数 λ \lambda λ,使得 x = λ y x = \lambda y x=λy,则 R P n = R n + 1 \ { 0 } / ∼ RP^n=\mathbb{R}^{n+1}\backslash \{ \bold{0} \} / \sim RPn=Rn+1\{0}/∼,即实射影空间是等价关系 ∼ \sim ∼ 下的等价类之集。
令 π : R n + 1 \ { 0 } → R P n \pi:\mathbb{R}^{n+1}\backslash \{ \bold{0} \} \rightarrow RP^n π:Rn+1\{0}→RPn 为投影,即 π ( u ) = [ u ] \pi(u)=[u] π(u)=[u],将非零向量 u u u 投影为 u u u 所张成的一维线性子空间(直线)。我们在 R P n RP^n RPn 中可取商拓扑,即 U U U 是 R P n RP^n RPn 中的开子集当且仅当其完全逆像 π − 1 ( U ) \pi^{-1}(U) π−1(U) 是 R n + 1 \ { 0 } \mathbb{R}^{n+1}\backslash \{ \bold{0} \} Rn+1\{0} 中的开子集。
如果在 S n S^n Sn 中取两个单位向量 x , y x, \; y x,y,规定 x ∼ y x\sim y x∼y 当且仅当 x = ± y x=\pm y x=±y,从而 R P n = S n / ∼ RP^n=S^n/\sim RPn=Sn/∼,这也是一个常见的形式。
我们来说明 R P n RP^n RPn 是一个 Hausdorff 空间。任取 u , v ∈ R n + 1 \ { 0 } u, v \in \mathbb{R}^{n+1}\backslash \{ \bold{0} \} u,v∈Rn+1\{0} 满足 u ≁ v u\nsim v u≁v,即 u , v u, \; v u,v 不在同一条过原点的直线上,显然 u ≠ v u \neq v u=v。则存在 R n + 1 \ { 0 } \mathbb{R}^{n+1}\backslash \{ \bold{0} \} Rn+1\{0} 中的两个开球 U , V U, \; V U,V 使得 u ∈ U u\in U u∈U, v ∈ V v \in V v∈V 为两球的球心,且 U ∩ V = ∅ U \cap V = \varnothing U∩V=∅。因为 u , v u, \; v u,v 与原点的两根连线不重合,故当 U , V U, \; V U,V 的半径充分小时,始点在原点且终点取自于 U U U 的任何向量与始点在原点且终点取自于 V V V 的任意向量是始终没有重合的,这意味着 ∀ p 1 ∈ U \forall p_1 \in U ∀p1∈U, ∀ p 2 ∈ V \forall p_2 \in V ∀p2∈V,都有 p 1 ≁ p 2 p_1 \nsim p_2 p1≁p2。故得 R P n RP^n RPn 的两个子集 π ( U ) ∩ π ( V ) = ∅ \pi(U)\cap \pi(V)=\varnothing π(U)∩π(V)=∅。下面说明这两个子集是开集。
我们知道 U , V U, \; V U,V 是 R n + 1 \ { 0 } \mathbb{R}^{n+1}\backslash \{ \bold{0} \} Rn+1\{0} 中的两个开球,而 π − 1 ( π ( U ) ) ⊇ U \pi^{-1}(\pi(U)) \supseteq U π−1(π(U))⊇U。事实上, π − 1 ( π ( U ) ) \pi^{-1}(\pi(U)) π−1(π(U)) 为由过原点的一族直线所包围的( n + 1 n+1 n+1 维)开圆锥(不含边界和原点)部分。如下图所示(画图比较简陋,实属不会画图):

显然, π − 1 ( π ( U ) ) \pi^{-1}(\pi(U)) π−1(π(U)) 是 R n + 1 \ { 0 } \mathbb{R}^{n+1}\backslash \{ \bold{0} \} Rn+1\{0} 中的开集。因此由投影定义,我们得到 π ( U ) \pi(U) π(U) 是射影空间 R P n RP^n RPn 的开集。同理 π ( V ) \pi(V) π(V) 也是开集,所以实射影空间是 Hausdorff 空间。
设 U i = { [ x ] = [ x 1 , x 2 , ⋯ , x n + 1 ] ∈ R P n ∣ x i ≠ 0 } U_i=\{ [x]=[x_1,x_2,\cdots,x_{n+1}] \in RP^n \;| \;\; x_i \neq 0 \} Ui={[x]=[x1,x2,⋯,xn+1]∈RPn∣xi=0} 是 R P n RP^n RPn 中的一个开集,定义 ϕ i : U i → R n \phi_i: U_i \rightarrow \mathbb{R}^n ϕi:Ui→Rn 为:
ϕ i [ x 1 , x 2 , ⋯ , x n + 1 ] = ( x 1 / x i , ⋯ , x i − 1 / x i , x i + 1 / x i , ⋯ , x n + 1 / x i ) \phi_i[x_1,x_2,\cdots, x_{n+1}]=(x_1/x_i, \cdots, x_{i-1}/x_i,x_{i+1}/x_i, \cdots, x_{n+1}/x_i) ϕi[x1,x2,⋯,xn+1]=(x1/xi,⋯,xi−1/xi,xi+1/xi,⋯,xn+1/xi) 该定义是没有歧义的,如果是 [ λ x 1 , λ x 2 , ⋯ , λ x n + 1 ] [\lambda x_1,\lambda x_2,\cdots, \lambda x_{n+1}] [λx1,λx2,⋯,λxn+1] ,则仍然有 ϕ i [ λ x 1 , λ x 2 , ⋯ , λ x n + 1 ] = ϕ i [ x 1 , x 2 , ⋯ , x n + 1 ] \phi_i[\lambda x_1,\lambda x_2,\cdots, \lambda x_{n+1}]=\phi_i[x_1,x_2,\cdots, x_{n+1}] ϕi[λx1,λx2,⋯,λxn+1]=ϕi[x1,x2,⋯,xn+1]。
显然 ϕ i \phi_i ϕi 有逆映射(对 ϕ i [ x 1 , x 2 , ⋯ , x n + 1 ] \phi_i[x_1,x_2,\cdots, x_{n+1}] ϕi[x1,x2,⋯,xn+1] 式子取 x i = 1 x_i=1 xi=1 可得):
ϕ i − 1 ( y 1 , y 2 , ⋯ , y n ) = [ y 1 , y 2 , ⋯ , y i − 1 , 1 , y i , ⋯ , y n ] \phi_i^{-1}(y_1,y_2,\cdots, y_n)=[y_1,y_2,\cdots, y_{i-1},1,y_{i},\cdots,y_n] ϕi−1(y1,y2,⋯,yn)=[y1,y2,⋯,yi−1,1,yi,⋯,yn] 可以验证, ϕ i \phi_i ϕi 是从 U i U_i Ui 到 R n \mathbb{R}^n Rn 的同胚(证明待补充…)。
A = { ( U i , ϕ i ) ∣ 1 ≤ i ≤ n + 1 } \mathscr{A}=\{ (U_i, \phi_i) |\; 1\leq i \leq n+1 \} A={(Ui,ϕi)∣1≤i≤n+1} 是 R P n RP^n RPn 的坐标卡之集,从而 R P n RP^n RPn 是一个拓扑流形。 对于 i < j i<j i<j 考虑:
ϕ j ∘ ϕ i − 1 ( y 1 , y 2 , ⋯ , y n ) = ( y 1 / y j , ⋯ , 1 / y j , ⋯ , y j − 1 / y j , y j + 1 / y j , ⋯ , y n / y j ) \begin{align} &\phi_j \circ \phi_i^{-1}(y_1,y_2,\cdots,y_n) \\ &=(y_1/y_j,\cdots,1/y_j,\cdots,y_{j-1}/y_j,y_{j+1}/y_j,\cdots,y_n/y_j) \end{align} ϕj∘ϕi−1(y1,y2,⋯,yn)=(y1/yj,⋯,1/yj,⋯,yj−1/yj,yj+1/yj,⋯,yn/yj) 上述映射在 ϕ i ( U i ∩ U j ) \phi_i(U_i \cap U_j) ϕi(Ui∩Uj) 上显然是 C ∞ C^{\infty} C∞ 的,坐标卡集 A \mathscr{A} A 决定了 R P n RP^n RPn 上的光滑结构,故 R P n RP^n RPn 为光滑流形。
本节完。
相关文章:

微分流形学习之一:基本定义
微分流形学习之一:基本定义引入 引言一、微分流形的历史简介二、拓扑空间三、微分流形 引言 本文是作者在学习微分流形的时候的笔记,尽量严格完整,并带有一定理解,绝不是结论的简单罗列。如果读者知道数学分析中的 ϵ − δ \ep…...
[C++]笔记-制作自己的静态库
一.静态库的创建 在项目属性c/c里面,选用无预编译头,创建头文件与cpp文件,需要注意release模式下还是debug模式,在用库时候要与该模式相匹配,库的函数实现是外界无法看到的,最后在要使用的项目里面导入.h文件和.lib文件 二.使用一个循环给二维数组赋值 行数 : 第几个元素 / …...

优酷视频码率、爱奇艺视频码率、B站视频码率、抖音视频码率对比
优酷视频码率、爱奇艺视频码率与YouTube视频码率对比 优酷视频码率: 优酷的视频码率可以根据视频质量、分辨率和内容类型而变化。一般而言,优酷提供了不同的码率选项,包括较低的标清(SD)码率和较高的高清(…...
用pytorch实现google net
GoogleNet(也称为Inception v1)是由Google在2014年提出的一个深度卷积神经网络架构。它在ImageNet Large Scale Visual Recognition Challenge (ILSVRC) 2014比赛中取得了优秀的成绩,并引起了广泛的关注。 GoogleNet的设计目标是构建一个更…...

2023-8-15差分矩阵
题目链接:差分矩阵 #include <iostream>using namespace std;const int N 1010;int n, m, q; int a[N][N], b[N][N];void insert(int x1, int y1, int x2, int y2, int c) {b[x1][y1] c;b[x1][y2 1] - c;b[x2 1][y1] - c;b[x2 1][y2 1] c; }int main…...

物理公式分类
(99 封私信 / 81 条消息) 定义式和决定式有什么区别,怎么区分? - 知乎 (zhihu.com) 1、首先,定义一个物理符号(物理量)来表征物理世界最直观/最基本的物理现象,例如,长度(米…...

vue实现登录注册
目录 一、登录页面 二、注册页面 三、配置路由 一、登录页面 <template><div class"login_container" style"background-color: rgb(243,243,243);height: 93.68vh;background-image: url(https://ts1.cn.mm.bing.net/th/id/R-C.f878c96c4179c501a6…...
SpringBoot复习:(55)在service类中的方法上加上@Transactional注解后,Spring底层是怎么生成代理对象的?
SpringBoot run方法代码如下: 可以看到它会调用refreshContext方法来刷新Spring容器,这个refreshContext方法最终会调用AbstractApplicationContext的refresh方法,代码如下 如上图,refresh方法最终会调用finisheBeanFactoryInit…...

常用的图像校正方法
在数字图像处理中,常用的校正方法包括明场均匀性校正、查找表(LUT)校正和伽玛(Gamma)校正。这些校正方法分别针对不同的图像问题,可以改善图像质量,提升图像的可读性和可分析性。下面是这三种校…...

AWS security 培训笔记
云计算的好处 Amazon S3 (Storage) Amazon EC2 (Compute) 上图aws 的几个支柱:安全是其中一个啦 其中安全有几个方面 IAMdetection基础架构保护数据保护应急响应 关于云供应商的责任 data center 原来长这样 ,据说非常之隐蔽的 如果有天退役了…...
设计模式之代理模式(Proxy)的C++实现
1、代理模式的提出 在组件的开发过程中,有些对象由于某种原因(比如对象创建的开销很大,或者对象的一些操作需要做安全控制,或者需要进程外的访问等),会使Client使用者在操作这类对象时可能会存在问题&…...
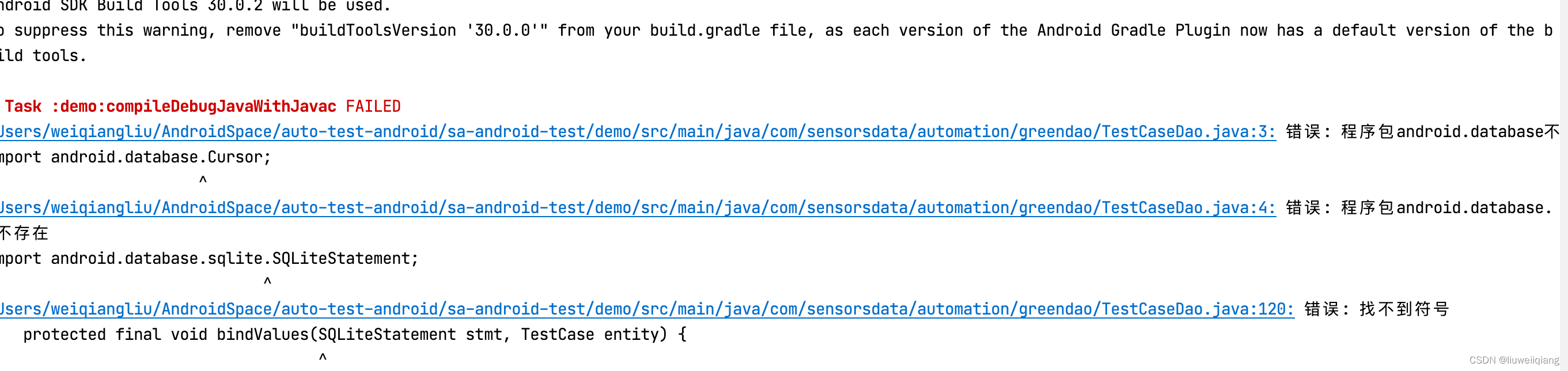
vim 配置环境变量与 JDK 编译器异常
vim 配置环境变量 使用 vim 打开系统中的配置信息(不存在将会创建): vim ~/.bash_profile 以配置两个版本 JDK 为例(前提是已安装 JDK),使用上述命令打开配置信息: 输入法调成英文,输入 i&…...

TiDB v7.1.0 跨业务系统多租户解决方案
本文介绍了 TiDB 数据库的资源管控技术,并通过业务测试验证了效果。资源管控技术旨在解决多业务共用一个集群时的资源隔离和负载问题,通过资源组概念,可以限制不同业务的计算和 I/O 资源,实现资源隔离和优先级调度,提高…...

【题解】二叉树中和为某一值的路径(一)
二叉树中和为某一值的路径(一) 题目链接:二叉树中和为某一值的路径(一) 解题思路1:递归 我们或许想记录下每一条从根节点到叶子节点的路径,计算出该条路径的和,但此种思路用递归稍麻烦,我们可以试着把和转换为差&am…...

css中变量和使用变量和运算
变量: 语法:--css变量名:值; --view-theme: #1a99fb; css使用变量: 语法:属性名:var( --css变量名 ); color: var(--view-theme); css运算: 语法:属性名…...

数据结构之线性表的类型运用Linear Lists: 数组,栈,队列,链表
线性表 定义 一个最简单,最基本的数据结构。一个线性表由多个相同类型的元素穿在一次,并且每一个元素都一个前驱(前一个元素)和后继(后一个元素)。 线性表的类型 常见的类型:数组、栈、队列…...

成瘾机制中微生物群的神秘角色
谷禾健康 成瘾是一种大脑疾病,受害者无法控制地对某种物质或行为产生强烈的依赖和渴求,尽管这种行为会产生有害的后果。成瘾包括一系列物质滥用障碍,例如药物、酒精、香烟,过度饮食。近年来,吸毒成瘾急剧上升ÿ…...

arm安装docker与docker-copose
一、银河麒麟Arm64安装docker 1、docker 安装包地址: https://download.docker.com/linux/static/stable 2、解压,然后将docker目录下文件拷贝到/usr/bin里 tar -xf docker-18.09.3.tgz mv docker/* /usr/bin/ 3、准备 docker.service系统配置文件 &…...

9.文件基本操作
第四章 文件管理 9.文件基本操作 “打开文件和关闭文件”与平常鼠标双击打开文件和点击“X”关闭文件是有所不同的。 操作系统在处理open系统调用时主要做了以下两件事情,①根据我们提供的文件存放路径在外存当中找到这个目录对应的目录表&#x…...

【Java】Spring——Bean对象的作用域和生命周期
文章目录 前言一、引出Bean对象的作用域1.普通变量的作用域2.Bean对象的作用域 二、Bean对象的作用域1.Bean对象的6种作用域2.设置Bean对象的作用域 三、Bean对象的生命周期总结 前言 本人是一个普通程序猿!分享一点自己的见解,如果有错误的地方欢迎各位大佬莅临指导,如果你也…...

数字孪生助力智慧水务:科技创新赋能水资源保护
智慧水务中,数字孪生有着深远的作用,正引领着水资源管理和环境保护的创新变革。随着城市化和工业化的不断推进,水资源的可持续利用和管理愈发显得重要,而数字孪生技术为解决这一挑战提供了独特的解决方案。 数字孪生技术…...

css 实现文字横向循环滚动
实现效果 思路 ## 直接上代码,html部分 //我这里是用的uniapp <view class"weather_info_wrap"><view class"weather_info">当前多云,今晚8点转晴,明天有雨,温度32摄氏度。</view><view class&qu…...

VuePress 数学公式支持
前言 博主在为 VuePress1.0 博客添加数学公式支持过程中遇到如下问题 问题一 在配置诸如 markdown-it-texmath,markdown-it-katex,markdown-it-mathjax3 这些插件后遇到 Error: Dynamic require of "XXX" is not supported 问题二 配置插件 vuepress-plugin-ma…...
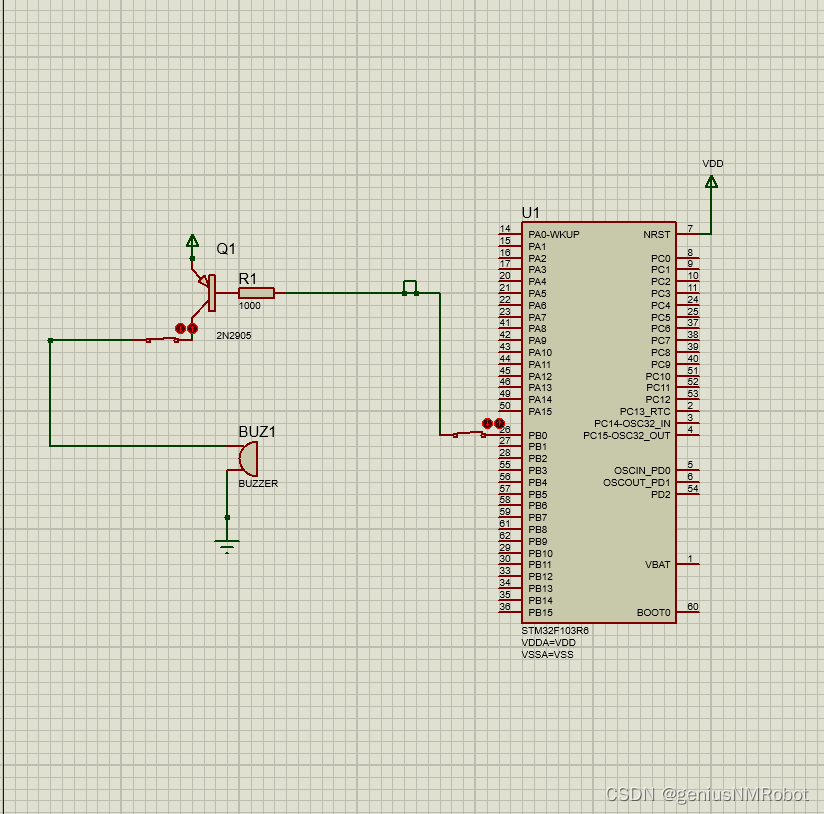
stm32控制蜂鸣器源代码(附带proteus线路图)
说明: 1 PB0输出0时,蜂鸣器发生; 2 蜂鸣器电阻值如果太大会导致电流太小,发不出声音; 3蜂鸣器额定电压需要设置得低一点,可以是2V,但不能高于3V,这更右上角的电阻值有关系&#x…...

selinux
一、selinux的说明 二、selinux的工作原理 三、selinux的启动、关闭与查看 Enforcing和permissive都是临时的,重启还是依据配置文件中,禁用selinux,修改配置文件: 之后重启生效 四、selinux对linux服务的影响...

使用opencv4.7.0部署yolov5
yolov5原理和部署原理就不说了,想了解的可以看看这篇部署原理文章 #include <fstream> #include <sstream> #include <iostream> #include <opencv2/dnn.hpp> #include <opencv2/imgproc.hpp> #include <opencv2/highgui.hpp>/…...
Python - 协程基本使用详解【demo】
一. 前言 协程(Coroutine)是一种轻量级的线程,也被称为用户级线程或绿色线程。它是一种用户态的上下文切换方式,比内核态的线程切换更为轻量级,能够高效的支持大量并发操作。 2. 使用协程的好处 Python 中的协程是通…...

Android MVVM架构模式,详详详细学习
MVVM(Model-View-ViewModel) 是一种基于数据绑定的架构模式,用于设计和组织应用程序的代码结构。它将应用程序分为三个主要部分:Model(模型)、View(视图)和ViewModel(视…...
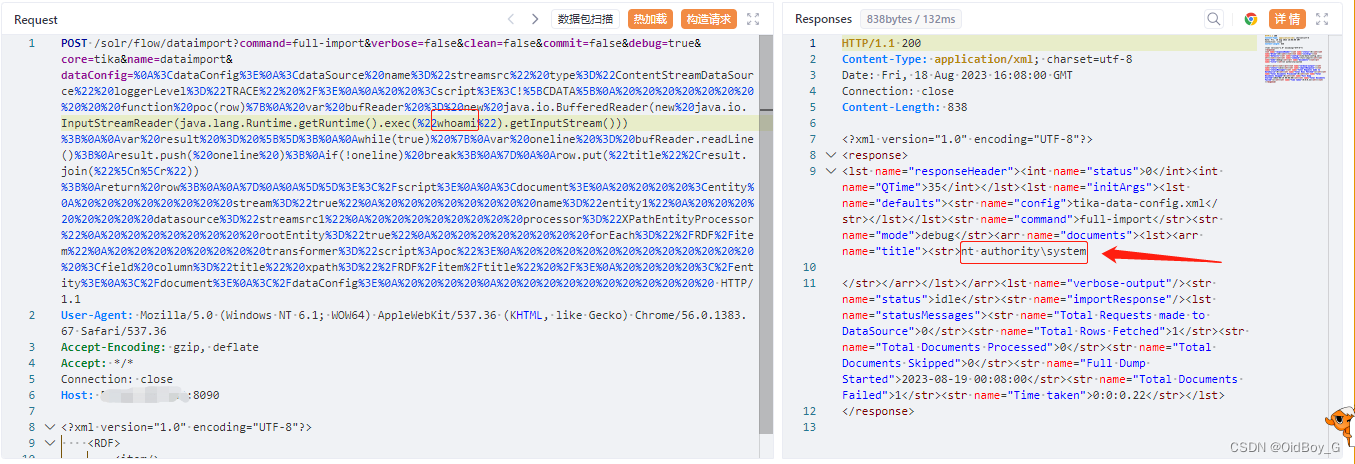
亿赛通电子文档安全管理系统 RCE漏洞复现
0x01 产品简介 亿赛通电子文档安全管理系统(简称:CDG)是一款电子文档安全加密软件,该系统利用驱动层透明加密技术,通过对电子文档的加密保护,防止内部员工泄密和外部人员非法窃取企业核心重要数据资产&…...
星际争霸之小霸王之小蜜蜂(三)--重构模块
目录 前言 一、为什么要重构模块 二、创建game_functions 三、创建update_screen() 四、修改alien_invasion模块 五、课后思考 总结 前言 前两天我们已经成功创建了窗口,并将小蜜蜂放在窗口的最下方中间位置,本来以为今天将学习控制小蜜蜂,结…...

JS的解析与Js2Py使用
JS的解析与Js2Py使用 JS的解析事件监听器搜索关键字请求关联JS文件 Js2PyJs2Py的简单使用安装Js2Py执行JavaScript代码调用JavaScript函数 Js2Py的应用示例创建JavaScript文件使用JavaScript JS的解析 在一个网站中,登录密码通常是会进行加密操作的,那么…...

Spring Bean的生命周期总结(包含面试题)
目录 一、Bean的初始化过程 1. 加载Spring Bean 2. 解析Bean的定义 3. Bean属性定义 4. BeanFactoryPostProcessor 扩展接口 5. 实例化Bean对象 6. Aware感知 7. 初始化方法 8. 后置处理 9. destroy 销毁 二、Bean的单例与多例模式 2.1 单例模式(Sin…...
SpringjDBCTemplate_spring25
1、首先导入两个包,里面有模板 2、transtion事务 jDbc操作对象,底层默认的是事务: 3、我们java一般对实体类进行操作。 4、第一步写好坐标。 创建一个Account表 数据修改用update 数据进去了...
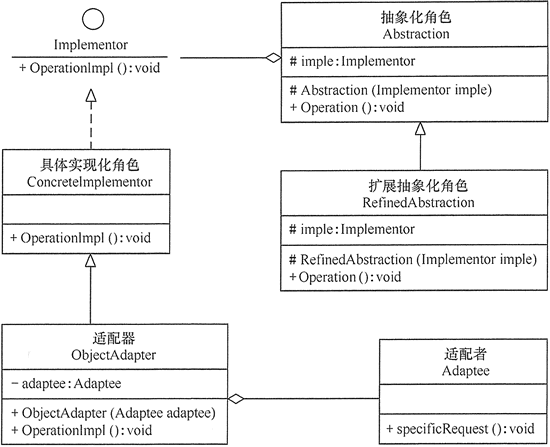
设计模式——桥接模式
引用 桥我们大家都熟悉,顾名思义就是用来将河的两岸联系起来的。而此处的桥是用来将两个独立的结构联系起来,而这两个被联系起来的结构可以独立的变化,所有其他的理解只要建立在这个层面上就会比较容易。 基本介绍 桥接模式(Br…...
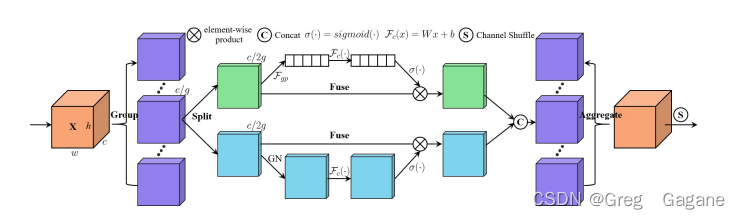
改进YOLO系列:2.添加ShuffleAttention注意力机制
添加ShuffleAttention注意力机制 1. ShuffleAttention注意力机制论文2. ShuffleAttention注意力机制原理3. ShuffleAttention注意力机制的配置3.1common.py配置3.2yolo.py配置3.3yaml文件配置1. ShuffleAttention注意力机制论文 论文题目:SA-NET: SHUFFLE ATTENTION …...

利用Opencv实现人像迁移
前言: Hello大家好,我是Dream。 今天来学习一下如何使用Opencv实现人像迁移,欢迎大家一起参与探讨交流~ 本文目录: 一、实验要求二、实验环境三、实验原理及操作1.照片准备2.图像增强3.实现美颜功能4.背景虚化5.图像二值化处理6.人…...

Lnton羚通算法算力云平台在环境配置时 OpenCV 无法显示图像是什么原因?
问题: cv2.imshow 显示图像时报错,无法显示图像 0%| | 0/1 [00:00<…...
【JavaEE进阶】MyBatis的创建及使用
文章目录 一. MyBatis简介二. MyBatis 使用1. 数据库和数据表的创建2. 创建Mybatis项目2.1 添加MyBatis框架支持2.2 设置MyBatis配置信息 3. MyBatis开发流程4. MyBatis查询数据库测试 三. MyBatis 流程1. MyBatis 查询数据库流程2. MyBatis 框架交互流程图 一. MyBatis简介 M…...

职业学院物联网实训室建设方案
一、概述 1.1专业背景 物联网(Internet of Things)被称为继计算机、互联网之后世界信息产业第三次浪潮,它并非一个全新的技术领域,而是现代信息技术发展到一定阶段后出现的一种聚合性应用与技术提升,是随着传感网、通…...
3 个 ChatGPT 插件您需要立即下载3 ChatGPT Extensions You need to Download Immediately
在16世纪,西班牙探险家皮萨罗带领约200名西班牙士兵和37匹马进入了印加帝国。尽管印加帝国的军队数量达到了数万,其中包括5,000名精锐步兵和3,000名弓箭手,他们装备有大刀、长矛和弓箭等传统武器。但皮萨罗的军队中有100名火枪手,…...
屏蔽socket 实例化时,握手阶段报错信息WebSocket connection to ‘***‘ failed
事情起因是这样的: 我们网站是需要socket链接实行实时推送服务,有恶意竞争对手通过抓包或者断网,获取到了我们的socket链接地址,那么他就可以通过java写一个脚本无限链接这个socket地址。形成dos攻击。使socket服务器资源耗尽&…...

单发多框检测(SSD)【动手学深度学习】
单发多框检测模型主要由一个基础网络块和若干多尺度特征块串联而成。基本网络用于从输入图像中提取特征,可以使用深度卷积神经网络,原论文中选用了在分类层之前阶段的VGG,现在也常用ResNet替代。 我们可以设计基础网络,使它输出的高和宽较大,这样基于该特征图生成的锚框数…...

“RFID与光伏板的完美融合:探索能源科技的新时代!“
随着科技的不断发展,人类创造出了许多令人惊叹的发明。其中,RFID(Radio Frequency Identification)技术的应用在各个领域日益广泛。最近的研究表明,将RFID技术应用于光伏板领域,不仅可以提高光伏板的效率&a…...

算法leetcode|71. 简化路径(rust重拳出击)
文章目录 71. 简化路径:样例 1:样例 2:样例 3:样例 4:提示: 分析:题解:rust:go:c:python:java: 71. 简化路径:…...

网络技术Vlan技术STP(第一课)
一 Vlan技术的学习 对命令的增删改查 #### 1)创建vlan[SW1]vlan 2 [2-4094] 创建vlan[SW1]vlan batch 10 20 30 创建多个不连续的vlan[SW1]display vlan 查看vlan信息[SW1]vlan batch 50 to 60创建多个连续的vlan[SW1]vlan2[SW1-vlan2]description caiwu添加描述信…...
SpringBoo t+ Vue 微人事 (十一)
职位修改操作 在对话框里面做编辑的操作 添加对话框 <el-dialogtitle"修改职位":visible.sync"dialogVisible"width"30%"><div><el-tag>职位名称</el-tag><el-input size"small" class"updatePosIn…...

自动驾驶卡车量产-第一章-用户需求
1、中国干线物流行业现状 万亿级市场,规模巨大。由中重卡承运的干线运输占到整体公路货运市场的82%,全国中重卡保有量约730 万台1,市场规模达4.6 万亿元1,体量全球第一,超过同城物流及乘用出租市场规模之和。同样&…...

Nginx 配置文件的完整指南 (一)
文章目录 一、简介1.1 配置文件一览 二、全局配置2.0 user2.1 worker_processes2.2 events模块2.3 http模块 三、server模块3.1 listen3.2 server_name3.3 location:请求处理位置 Nginx 配置文件的完整指南 (二) 一、简介 Nginx是一款高性能的Web服务器和反向代理服…...

css3+js 画出爱心特效
要使用CSS3和JavaScript绘制爱心特效,可以使用CSS3的动画和过渡效果来创建爱心的形状,并使用JavaScript来控制动画的触发和交互。以下是一个简单的示例代码: HTML: <div class"heart"></div> <button onclick&quo…...

蔚来李斌卖手机:安卓系统,苹果售价,一年一发
作者 | Amy 编辑 | 德新 车圈大佬的玩法真让人寻不着套路! 苹果的库克和小米的雷布斯,甚至是FF贾老板准备许久,都想分一块新能源车的蛋糕,蔚来李斌却反手进军手机界,从宣布造手机到手机入网仅仅隔了一年。 近期&a…...
