【机器学习】— 2 图神经网络GNN

一、说明
在推荐系统系列的第一部分中,我们讨论了任务和常用的各种类型的推荐系统,以及基于业务上下文的相关指标。在本文中,我们将在推荐系统的背景下概述图论和图神经网络(GNN)。
二、经典矩阵补全方法
推荐系统的一种流行技术是利用经典的机器学习方法进行矩阵补全,这是一种协同过滤方法。给定用户数 m 和数项 n,它旨在填充用户-项交互矩阵 R(维度为 mxn)中的缺失值。为了实现这一点,我们将每个用户和项目映射到大小为 k 的嵌入 — 向量空间中的抽象表示。这些嵌入可能会捕获电影类型或用户人口统计数据等特征,但很多时候是潜在的未知特征。生成用户嵌入矩阵 U(维度为 mxk)和项目嵌入矩阵 I(维度为 nxk)。 为了预测用户-项目对,我们计算转置项目矩阵和用户矩阵的点积。最初,潜在矩阵是随机初始化的,我们使用基于已知用户-项交互的损失函数优化嵌入。

图 1:此图显示了用户-项交互矩阵 R,以及我们如何在用户和项嵌入矩阵之间取点积来预测 R 矩阵中的特定值。
但是,此方法在处理稀疏矩阵时会遇到性能问题。在用户仅与数百万个可用项中的几个项交互的情况下,经典的矩阵完成方法可能是不够的,因为它们只考虑用户和项之间的直接连接。为了解决这一限制,基于图神经网络(GNN)的推荐系统已成为一种更有效的替代方案。
GNN 不仅通过考虑单个用户的偏好,还集成来自相邻用户的信息,在稀疏数据集中提供改进的性能。通过利用图形结构,GNN 可以更全面地捕获用户和项目之间的关系,从而实现更准确和个性化的推荐。让我们首先提醒自己一些关于图论的知识。
三、图论概述
3.1 什么是图表?
图形是一种数据结构,将实体集合表示为节点(顶点),并将其关系表示为边。它是建模和理解各种真实场景的强大工具。例如,图表可以表示银行交易,其中节点符号化银行账户,边表示它们之间的交易。同样,社交网络图以人为节点,边缘描绘个人之间的关系。

图 2:图形示例。
图表的类型
根据其特征,有不同类型的图形。 有向图具有具有特定方向的边。 例如,在银行交易图中,每条边表示从发送方到接收方的交易,从而建立明确的方向。另一方面,无向图不会为边分配方向。在社交网络中,无向边缘表示两个人之间的联系或相识,没有任何固有的方向性。
图形也可以分为同构或异构。 同类图具有单一类型的节点和边,而异构图可能包含多种类型。例如,在电子商务方案中,可能有两种类型的节点:一种表示可供销售的商品,另一种表示用户。不同类型的边缘可以表示不同的交互,例如用户单击项目或进行购买。
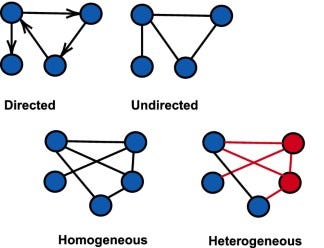
图 3:有向图、无向图、齐次图和异构图的示例
二分图是一种特定类型的异构图,在建模推荐系统方面非常有用。它们涉及两组不同的节点,例如用户和项目,边缘专门连接来自不同集的节点。二分图有效地捕获用户-项目交互,并启用高效的推荐算法来利用丰富的网络结构。
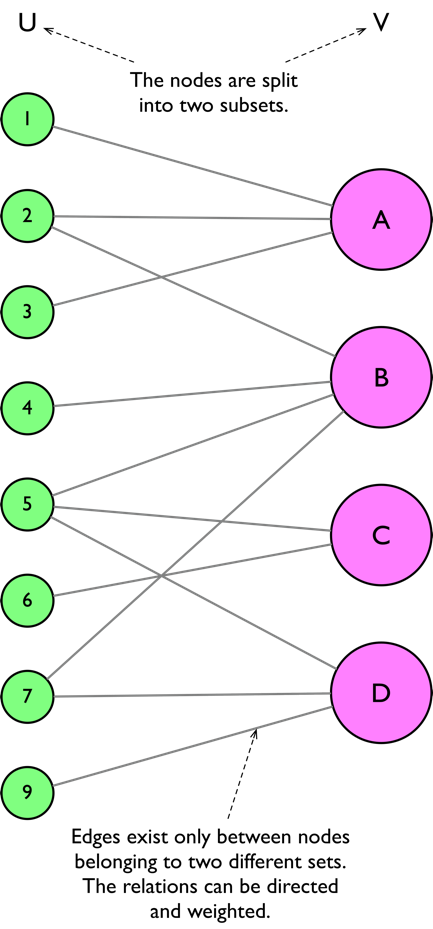
图 4:二分图示例。
3.2 我们如何存储图形数据?
有多种方法可以存储图形数据。一种方法是使用邻接矩阵,表示为 A ∈ {0, 1}ⁿxⁿ,其中 n 是图中的节点数。矩阵的 (i, j) 条目 Ai,j 表示节点 vi 和 vj 之间的连通性,如果有连接 vi 和 vj 的边,则为 Ai,j = 1。对于无向图,邻接矩阵是对称的,即 Ai,j = Aj,i。但是,对于大型和稀疏图(如社交网络),邻接矩阵可能是内存密集型的。这是因为邻接矩阵随节点数而缩放。在拥有数百万个节点的社交网络中,大多数人彼此不认识。这将导致一个大矩阵,其中大多数单元格为空。
为了解决这个问题,邻接列表表示形式对内存效率更高。 它将节点之间的边描述为元组 (i,j),其中 (0,1) 表示节点 0 和 1 之间的边。例如,对于图 5 中的图形,邻接列表为 [(A,B)、(B,D)、(B,C)、(D,C)]。
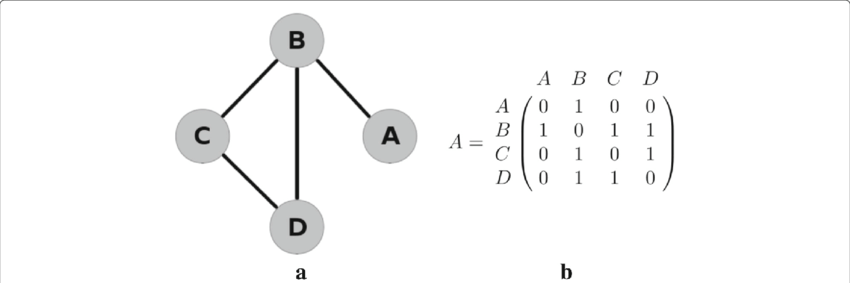
图 5a:图形示例 — 图 5b:图 4a 中图形的邻接矩阵。
邻接列表表示形式提供了更高的内存效率,特别是对于稀疏图,因为它仅存储有关连接节点的必要信息。这使其成为处理大规模图形数据(例如社交网络)的首选,其中连接数与节点总数相比通常有限。
四、推荐系统中的图神经网络
与传统的矩阵完成方法类似,GNN 可以为用户和项目生成嵌入,以预测看不见的用户-项目交互。但是,它们提供了一种显式合并高阶图结构的方法,并且可以捕获数据本身中可能不可用的潜在或隐藏相关性。
给定一个图,我们的目标是将每个节点 v 映射到其自己的 d 维最终嵌入,其中基于其网络邻域特征以及自身特征的相似节点最终应在其最终嵌入空间中彼此接近。

图 6:节点编码到嵌入空间。
4.1 图形神经网络层
GNN 的一层在图中的所有直接邻居之间交换信息,为图中的每个节点生成新的节点嵌入。在 2 层 GNN 模型中,每个节点将根据其 2 跳邻域生成其第 2 层嵌入。 K-hop 邻域是指距离感兴趣节点 K 边的所有节点。这是一个迭代过程,其中邻居变量通过传递消息(一种消息传递方法)与每个变量“对话”。
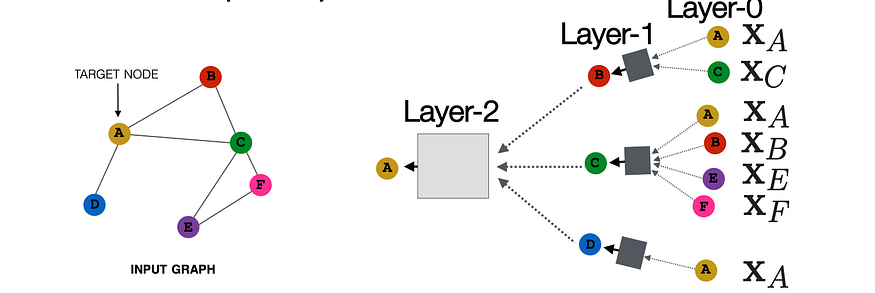
图 7:2 层 GNN 中特定目标节点的输入图和计算图
在此图像中,我们看到节点 A 的第 2 层表示是通过以某种方式聚合其直接邻居 [B,C,D] 的第 1 层嵌入并对其应用黑盒转换或神经网络生成的。这些嵌入又由其第 0 层 [X_A、X_B...X_F] 嵌入直接相邻要素,这是初始输入要素。每一层都会生成一个新的节点嵌入,节点的 K 层嵌入从距离自身的 K 跳节点获取信息。
4.2 图神经网络的特点、优势和局限性
图神经网络(GNN)具有几个显着的特征和优势,使其与传统的矩阵补全方法区分开来。这些特征有助于它们在推荐系统中的有效性。让我们探索这些功能:
- 阶次不变性: GNN 是顺序不变的,这意味着节点的标记顺序不会影响结果。计算图考虑节点连接而不是节点顺序,利用顺序不变的聚合函数(如平均值、最大/最小池化)进行消息传递。
- 大小不变性: GNN 中的每个节点都有自己的计算图,这使得 GNN 的大小不变。这允许各个节点根据其本地邻域处理和集成信息,从而实现个性化和灵活的学习。下图显示了上图中每个节点的计算图。
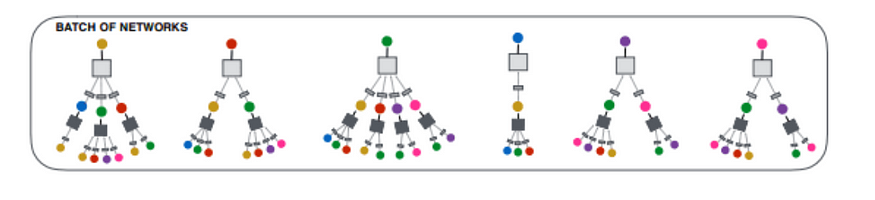
图 8:图 7 输入图中每个节点的计算图。
- 处理稀疏矩阵:与经典的矩阵补全方法不同,GNN 擅长处理稀疏矩阵。它们超越了直接节点交互,并捕获了高阶图结构中存在的隐藏相关性。此功能增强了它们在交互受限的场景中的性能
- 端到端学习: GNN 提供端到端学习,同时优化嵌入和预测任务。这减轻了对手动特征工程的需求,简化了推荐管道。此外,GNN 可以很好地适应不断发展的用户/项目功能,从而减少对重大代码修改的需求。
尽管GNN具有优势,但它们也有应考虑的局限性:
- 计算复杂性:GNN 可能是计算密集型的,特别是对于大型图形和深度架构。与更简单的模型相比,训练GNN可能需要大量的计算资源和更长的训练时间。
- 可解释性:与传统方法相比,GNN的复杂性可能使它们的可解释性降低。了解基于 GNN 的建议背后的内部工作原理和推理可能具有挑战性。
五、结论
通过利用嵌入在图结构中的丰富信息,GNN可以捕获复杂的模式,发现潜在特征,并在推荐过程中考虑相邻用户的影响。这种方法增强了推荐系统做出准确预测的能力,即使在经典方法难以生存的稀疏数据集中也是如此。
随着推荐系统领域的不断发展,GNN已成为解决传统方法局限性的有前途的解决方案。 他们适应不同领域并自动从数据中学习的能力使他们非常适合在各种情况下提供相关和量身定制的建议。
在本系列的下一部分中,我们将深入研究GNN的数学基础,特别关注LightGCN在电影推荐系统中的应用。通过了解基本原理和算法,我们可以进一步了解GNN如何改变推荐系统的格局。
相关文章:

【机器学习】— 2 图神经网络GNN
一、说明 在本文中,我们探讨了图神经网络(GNN)在推荐系统中的潜力,强调了它们相对于传统矩阵完成方法的优势。GNN为利用图论来改进推荐系统提供了一个强大的框架。在本文中,我们将在推荐系统的背景下概述图论和图神经网…...

QT的布局与间隔器介绍
布局与间隔器 1、概述 QT中使用绝对定位的布局方式,无法适用窗口的变化,但是,也可以通过尺寸策略来进行 调整,使得 可以适用窗口变化。 布局管理器作用最主要用来在qt设计师中进行控件的排列,另外,布局管理…...

深入浅出Pytorch函数——torch.nn.Linear
分类目录:《深入浅出Pytorch函数》总目录 对输入数据做线性变换 y x A T b yxA^Tb yxATb 语法 torch.nn.Linear(in_features, out_features, biasTrue, deviceNone, dtypeNone)参数 in_features:[int] 每个输入样本的大小out_features :…...

Vue3.2+TS的defineExpose的应用
defineExpose通俗来讲,其实就是讲子组件的方法或者数据,暴露给父组件进行使用,这样对组件的封装使用,有很大的帮助,那么defineExpose应该如何使用,下面我来用一些实际的代码,带大家快速学会defi…...

牛客网Python入门103题练习|【08--元组】
⭐NP62 运动会双人项目 描述 牛客运动会上有一项双人项目,因为报名成功以后双人成员不允许被修改,因此请使用元组(tuple)进行记录。先输入两个人的名字,请输出他们报名成功以后的元组。 输入描述: 第一…...
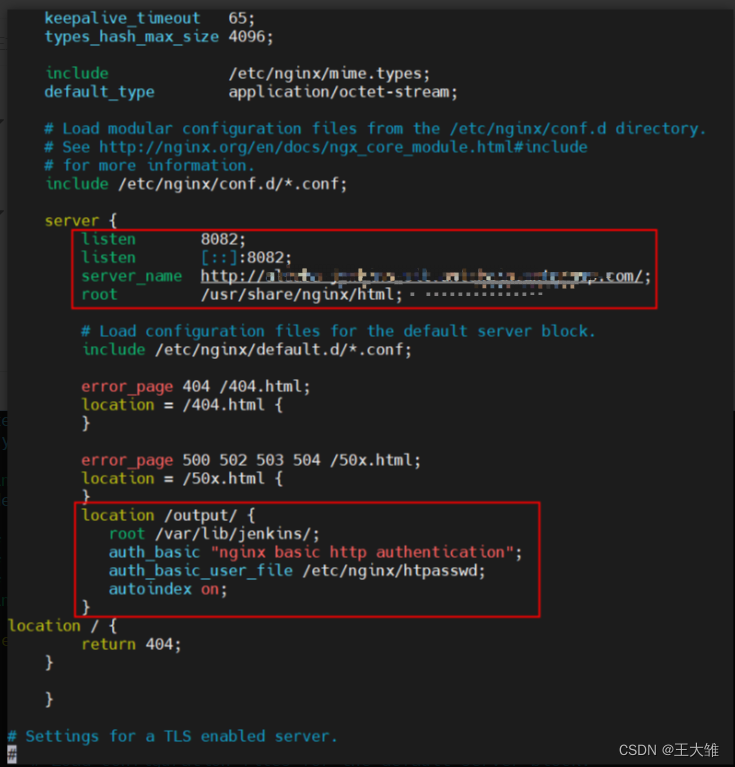
Jenkins改造—nginx配置鉴权
先kill掉8082的端口进程 netstat -natp | grep 8082 kill 10256 1、下载nginx nginx安装 EPEL 仓库中有 Nginx 的安装包。如果你还没有安装过 EPEL,可以通过运行下面的命令来完成安装 sudo yum install epel-release 输入以下命令来安装 Nginx sudo yum inst…...
VisionOS平台概述)
(二)VisionOS平台概述
2.VisionOS平台概述 1. VisionOS平台概述 Unity 对VisionOS的支持将 Unity 编辑器和运行时引擎的全部功能与RealityKit提供的渲染功能结合起来。Unity 的核心功能(包括脚本、物理、动画混合、AI、场景管理等)无需修改即可支持。这允许游戏和应用程序逻…...

菜单中的类似iOS中开关的样式
背景是我们有需求,做类似ios中开关的按钮。github上有一些开源项目,比如 SwitchButton, 但是这个项目中提供了很多选项,并且实际使用中会出现一些奇怪的问题。 我调整了下代码,把无关的功能都给删了,保留核…...

Vue 2 动态组件和异步组件
先阅读 【Vue 2 组件基础】中的初步了解动态组件。 动态组件与keep-alive 我们知道动态组件使用is属性和component标签结合来切换不同组件。 下面给出一个示例: <!DOCTYPE html> <html><head><title>Vue 动态组件</title><scri…...
MongoDB升级经历(4.0.23至5.0.19)
MongoDB从4.0.23至5.0.19升级经历 引子:为了解决MongoDB的两个漏洞决定把MongoDB升级至最新版本,期间也踩了不少坑,在这里分享出来供大家学习与避坑~ 1、MongoDB的两个漏洞 漏洞1:MongoDB Server 安全漏洞(CVE-2021-20330) 漏洞2…...
iPhone上的个人热点丢失了怎么办?如何修复iPhone上不见的个人热点?
个人热点功能可将我们的iPhone手机转变为 Wi-Fi 热点,有了Wi-Fi 热点后就可以与附近的其他设备共享其互联网连接。 一般情况下,个人热点打开就可以使用,但也有部分用户在升级系统或越狱后发现 iPhone 的个人热点消失了。 iPhone上的个人热点…...
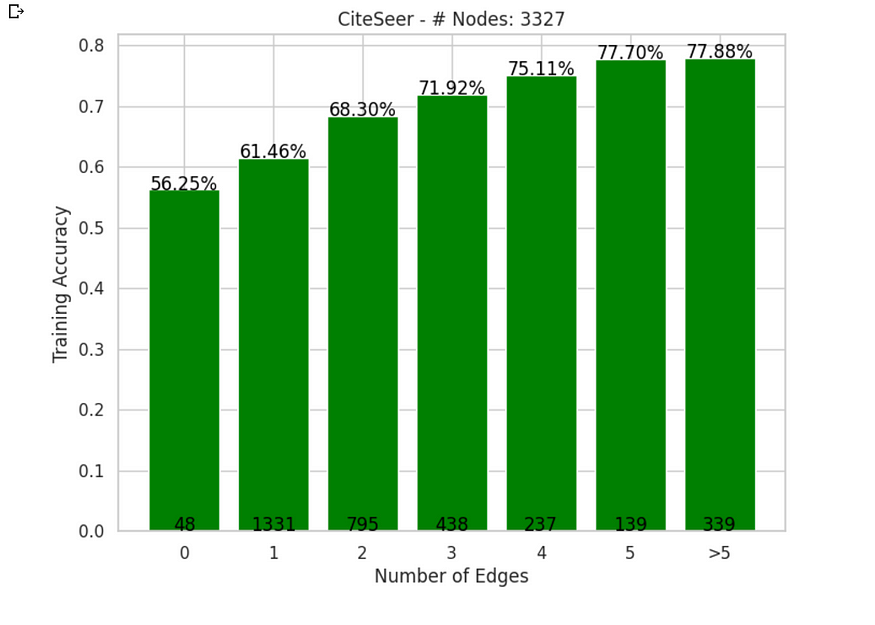
AI 媒人:为什么图形神经网络比 MLP 更好?
一、说明 G拉夫神经网络(GNN)!想象他们是人工智能世界的媒人,通过探索他们的联系,不知疲倦地帮助数据点找到朋友和人气。数字派对上的终极僚机。 现在,为什么这些GNN如此重要,你问?好…...

信息学奥赛一本通 1984:【19CSPJ普及组】纪念品 | 洛谷 P5662 [CSP-J2019] 纪念品
【题目链接】 ybt 1984:【19CSPJ普及组】纪念品 洛谷 P5662 [CSP-J2019] 纪念品 【题目考点】 1. 动态规划:完全背包 【解题思路】 由于小伟每天都可以买卖物品无限次,我们可以假想每天开始时,他把所有的商品都卖出ÿ…...

JVM——JVM参数指南
文章目录 1.概述2.堆内存相关2.1.显式指定堆内存–Xms和-Xmx2.2.显式新生代内存(Young Ceneration)2.3.显示指定永久代/元空间的大小 3.垃圾收集相关3.1.垃圾回收器3.2.GC记录 1.概述 在本篇文章中,你将掌握最常用的 JVM 参数配置。如果对于下面提到了一些概念比如…...

马上七夕到了,用各种编程语言实现10种浪漫表白方式
目录 1. 直接表白:2. 七夕节表白:3. 猜心游戏:4. 浪漫诗句:5. 爱的方程式:6. 爱心Python:7. 心形图案JavaScript 代码:8. 心形并显示表白信息HTML 页面:9. Java七夕快乐:…...
Spring Clould 注册中心 - Eureka,Nacos
视频地址:微服务(SpringCloudRabbitMQDockerRedis搜索分布式) Eureka 微服务技术栈导学(P1、P2) 微服务涉及的的知识 认识微服务-服务架构演变(P3、P4) 总结: 认识微服务-微服务技…...

使用appuploader工具发布证书和描述性文件教程
使用APPuploader工具发布证书和描述性文件教程 之前用AppCan平台开发了一个应用,平台可以同时生成安卓版和苹果版,想着也把这应用上架到App Store试试,于是找同学借了个苹果开发者账号,但没那么简单,还要用到Mac电脑的…...
【面试八股文】每日一题:谈谈你对IO的理解
谈谈你对IO的理解 每日一题-Java核心-谈谈你对对IO的理解【面试八股文】 1.Java基础知识 Java IO(Input/Output)是Java编程语言中用于处理输入和输出的一组类和接口。它提供了一种在Java程序中读取和写入数据的方法。 Java IO包括两个主要的部分&#x…...

200. 岛屿数量
思路:遍历整个矩阵,对每个格子执行以下操作: 如果格子是陆地(‘1’),则将其标记为已访问(‘0’),并从当前位置开始进行深度优先搜索,将与当前格子相邻的陆地都…...

【LeetCode】581.最短无序连续子数组
题目 给你一个整数数组 nums ,你需要找出一个 连续子数组 ,如果对这个子数组进行升序排序,那么整个数组都会变为升序排序。 请你找出符合题意的 最短 子数组,并输出它的长度。 示例 1: 输入:nums [2,6…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
