背包 问题
1、背包问题
1.1、01背包
题目:
有n件物品和一个容量为m的背包,第i件物品的体积是v[ i ],价值是w[ i ],每件物品只有一件,求在不超过背包容量的前提下,可以放的物品的最大价值是多少
基本思路:
每个物品只有一件,考虑去或者不取
状态设计:
//二维
状态表示:f[i][j]集合:从前i个物品中选,总体积不超过j的物品的价值属性:max
状态计算:选第i个物品:f[i][j]=min(f[i-1][j-v[i]]+w[i],f[i][j]);不选第i个物品:f[i][j]=min(f[i-1][j],f[i][j]);//时间复杂度基本无法优化,空间复杂度可以优化
//一维:由于每一次状态计算时仅需考虑计算上一个物品后的状态,但需要从m~0枚举体积
状态计算:f[j]=max(f[j],f[j-v[i]]+w[i]);代码:
//不优化:二维
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;
const int N=1100;
int f[N][N];
int w[N],v[N];
int n,m;
int res;int main()
{cin>>n>>m;for(int i=1;i<=n;i++) cin>>v[i]>>w[i];for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){f[i][j]=f[i-1][j];if(j>=v[i])f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);}}for(int i=1;i<=m;i++) res=max(f[n][i],res);cout<<res;return 0;
}
//优化·一维
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;
const int N = 1111;
int f[N];
int n,m;
int v[N],w[N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++) cin>>v[i]>>w[i];for(int i=1;i<=n;i++){for(int j=m;j>=v[i];j--){f[j]=max(f[j],f[j-v[i]]+w[i]);}}cout<<f[m];return 0;
}
1.2、完全背包
题目:
有n件物品和一个容量为m的背包,第i件物品的体积是v[ i ],价值是w[ i ],每件物品有无限多件,求在不超过背包容量的前提下,可以放的物品的最大价值是多少
基本思路:
由于每种物品有无限多件,所以对于每种物品有无限多种选择(选0个,选1个······选n个)
状态设计:
状态表示:f[i][j]集合:从前i个物品中选,总体积不超过j的物品的价值属性:max
状态计算://朴素O(n^3):枚举每件物品取多少件(k:0~j/v[i])f[i][j]=max(f[i][j],f[i-k][j-k*v[i]]+k*w[i])//优化:朴素版本时:f[i][j] =max{f[i-1][j], f[i-1][j-v[i]]+w[i], f[i-2][j-2*v[i]]+2*w[i]. ······ }f[i][j-v[i]] =max{ f[i-1][j-v[i]], f[i-2][j-2*v[i]]+w[i]. ······ }由以上两个式子可知:不选第i个:f[i][j]=f[i-1][j]选第i个(不确定个数):f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);//优化为一维f[j]=max(f[j],f[j-v[i]]+w[i])代码:
//朴素做法 会超时
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;int n,m;
const int N = 1111;
int v[N],w[N];
int f[N][N];int main()
{cin>>n>>m;for(int i=1;i<=n;i++) cin>>v[i]>>w[i];for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){for(int k=0;k*v[i]<=j;k++){f[i][j]=max(f[i-1][j-k*v[i]]+k*w[i],f[i][j]);}}}cout<<f[n][m];return 0;
}优化版本(二维)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;int n,m;
const int N = 1111;
int v[N],w[N];
int f[N][N];int main()
{cin>>n>>m;for(int i=1;i<=n;i++) cin>>v[i]>>w[i];for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){f[i][j]=f[i-1][j];if(j>=v[i]){f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);}}}cout<<f[n][m];return 0;
}//再优化版本(一维)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;int n,m;
const int N = 1111;
int v[N],w[N];
int f[N];int main()
{cin>>n>>m;for(int i=1;i<=n;i++) cin>>v[i]>>w[i];for(int i=1;i<=n;i++){for(int j=v[i];j<=m;j++){f[j]=max(f[j],f[j-v[i]]+w[i]);}}cout<<f[m];return 0;
}
1.3、多重背包
题目:
有n种物品和一个容量为m的背包,第 i 种物品有s[ i ]件,每件体积是v[ i ],价值是w[ i ],求在不超过背包容量的前提下,可以放的物品的最大价值是多少
基本思路(二进制优化版本):
任何一个数可以用二进制来表示,也就是20、21、……、2n 其中一项或几项的和
对于每一种物品划分为k组,每组的数量为2的倍数
然后转换为01背包进行考虑
状态设计:
同01背包
代码
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;
const int N=25000;
int n,m;
int w[N],v[N];
int f[N];int main()
{cin>>n>>m;int cnt=0;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){int a,b,s;cin>>a>>b>>s;int k=1;while(s>=k){cnt++;v[cnt]=a*k;w[cnt]=b*k;s-=k;k*=2;}if(s){cnt++;v[cnt]=a*s;w[cnt]=b*s;}}}n=cnt;for(int i=1;i<=n;i++){for(int j=m;j>=v[i];j--){f[j]=max(f[j],f[j-v[i]]+w[i]);}}cout<<f[m];
}
1.4、分组背包
题目:
有n件物品(可以被分成几组)和一个容量为m的背包,第i件物品的体积是v[ i ],价值是w[ i ],组号为p[ i ],每组只能选一个物品,求在不超过背包容量的前提下,可以放的物品的最大价值是多少
基本思路:
对于每组物品考虑取(取哪一件)或者不取
状态设计:
状态表示:f[i][j]集合:从前i组中选,总体积不超过j的物品的价值属性:max
状态计算:第i组不选:f[i][j]=f[i-1][j]选第i组的第k个:f[i][j]=max(f[i-1][j-v[i][k]]+w[i][k])//优化为一维f[j]=max(f[j],f[j-v[i][k]]+w[i][k])
代码:
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;
int n,m;
int w[110][110],v[110][110];
int s[110];
//二维 int f[110][110];
int f[110];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>s[i];for(int j=1;j<=s[i];j++) scanf("%d%d",&v[i][j],&w[i][j]);}/*二维for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){f[i][j]=f[i-1][j];for(int k=0;k<=s[i];k++){if(j-v[i][k]>=0){f[i][j]=max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]);}}}}cout<<f[n][m];*/for(int i=1;i<=n;i++){for(int j=m;j>=0;j--){f[j]=f[j];for(int k=0;k<=s[i];k++){if(j-v[i][k]>=0){f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);}}}}cout<<f[m];return 0;
}
1.5、混合背包
题目:
将1.1、1.2、1.3三种背包混合起来,即有的物品只可以取一次(01背包),有的物品可以取无限次(完全背包),有的物品可以取的次数有一个上限(多重背包)。
基本思路:
同上,分情况考虑各物品
状态设计:
同上
例题+代码:
有N种物品和一个容量是 V的背包。
物品一共有三类:
第一类物品只能用1次(01背包);
第二类物品可以用无限次(完全背包);
第三类物品最多只能用 si 次(多重背包);
每种体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N=1010;int n,m;
int v[N],w[N],s[N];
int f[N];int main()
{cin>>n>>m;for(int i=1;i<=n;i++){scanf("%d%d%d",&v[i],&w[i],&s[i]);if(s[i]==-1) s[i]=1;}for(int i=1;i<=n;i++){if(s[i]==0){for(int j=v[i];j<=m;j++){f[j]=max(f[j],f[j-v[i]]+w[i]);}}else{for(int k=1;k<=s[i];k*=2){for(int j=m;j>=k*v[i];j--){f[j]=max(f[j],f[j-k*v[i]]+k*w[i]);}s[i]-=k;}if(s[i]){for(int j=m;j>=s[i]*v[i];j--){f[j]=max(f[j],f[j-s[i]*v[i]]+s[i]*w[i]);}}}}cout<<f[m];
}
1.6、二维费用的背包
题目:
对于每种物品有两个限制条件,即除了对体积有限制外,还有一个限制量
基本思路:
增加了一重限制,所以需要增加一维变量
状态设计:
状态表示:f[i][j][k]集合:从前i个中选,体积不超过j,重量不超过k的价值区间:max
状态计算:同上
代码:
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;
const int N=1010;int n,M,W;
int v[N],m[N],w[N];
int f[110][110];int main()
{cin>>n>>M>>W;for(int i=1;i<=n;i++) scanf("%d%d%d",&v[i],&m[i],&w[i]);for(int i=1;i<=n;i++){for(int j=M;j>=v[i];j--){for(int k=W;k>=m[i];k--){f[j][k]=max(f[j][k],f[j-v[i]][k-m[i]]+w[i]);}}}cout<<f[M][W];return 0;
}
相关文章:

背包 问题
1、背包问题 1.1、01背包 题目: 有n件物品和一个容量为m的背包,第i件物品的体积是v[ i ],价值是w[ i ],每件物品只有一件,求在不超过背包容量的前提下,可以放的物品的最大价值是多少 基本思路ÿ…...

蓝牙资讯|安卓将加强耳机音量监控,耳机查找功能将更加普遍
为了保护用户的听力健康,Android 14 将增加一项新功能,当用户使用耳机听音乐时,如果音量过高或持续时间过长,系统会发出警告,并自动降低音量。这个功能叫做“耳机音量过高警告(headphone loud sound alert&…...
vue,element。监听快捷键粘贴图片,添加到el-upload的列表。
在①中,粘贴图片,图片能够自动添加到底下el-upload组件的文件列表②。 // 对应① <el-card><el-tooltip content"粘贴图片至此" placement"top"><input readonly class"pasteImg" paste.prevent"hand…...
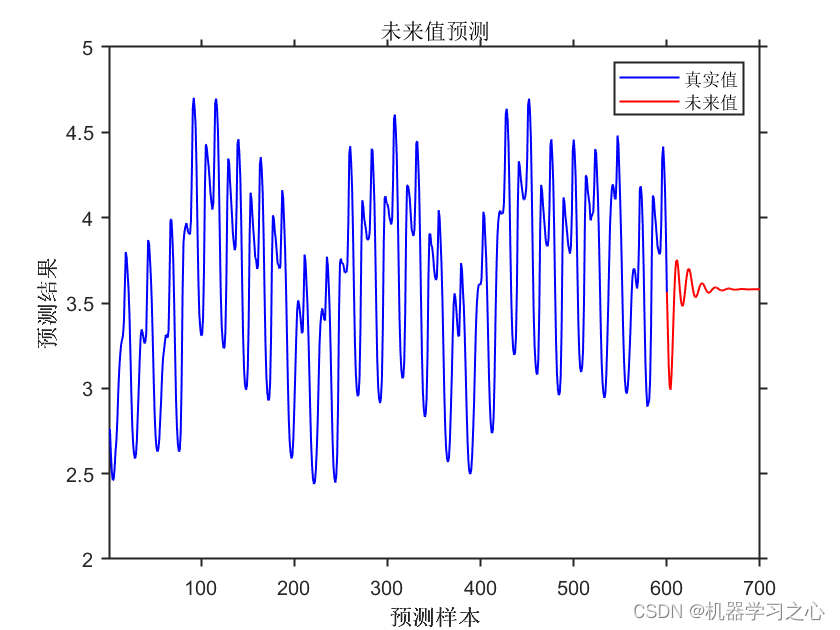
时序预测 | MATLAB实现基于CNN-BiLSTM卷积双向长短期记忆神经网络的时间序列预测-递归预测未来(多指标评价)
时序预测 | MATLAB实现基于CNN-BiLSTM卷积双向长短期记忆神经网络的时间序列预测-递归预测未来(多指标评价) 目录 时序预测 | MATLAB实现基于CNN-BiLSTM卷积双向长短期记忆神经网络的时间序列预测-递归预测未来(多指标评价)预测结果基本介绍程序设计参考资料 预测结果 基本介绍…...

编织梦想:SpringBoot AOP 教程与自定义日志切面完整实战
什么是 AOP AOP 是指通过预编译方式和运行期动态代理的方式,在不修改源代码的情况下对程序进行功能增强的一种技术。AOP 不是面向对象编程(OOP)的替代品,而是 OOP 的补充和扩展。它是一个新的维度,用来表达横切问题&a…...

AssignableTypeFilter 和 AnnotationTypeFilter什么区别?
在 Spring 框架中,AssignableTypeFilter 和 AnnotationTypeFilter 都是用于在组件扫描过程中进行过滤的工具类,用于筛选出特定类型或特定注解的类。它们的主要区别在于筛选的侧重点和使用方式。 AssignableTypeFilter: AssignableTypeFilte…...

TCP-事件模型
#include "main.h"VOID Server_write_error() {}/*1.打开网络库 * 2.校验网络库版本 * 3.创建SOCKET * 4.绑定IP地址和端口 * 5.开始监听 * 6.创建客户端socket/接受链接 * 7.与客户端收发消息 * 8.(6.7)两步的函数accept,send,recv 有堵塞,可…...
typescript 声明文件
作用 1、为已存在js库提供类型信息,这样在ts项目中使用这些库时候,就像用ts一样,会有代码提示、类型保护等机制 2、项目内共享类型:如果多个.ts文件中都用到同一个类型,此时可以创建.d.ts文件提供该类型,…...

BC96 有序序列判断
描述 输入一个整数序列,判断是否是有序序列,有序,指序列中的整数从小到大排序或者从大到小排序(相同元素也视为有序)。 数据范围:3≤n≤50 序列中的值都满足1≤val≤100。 输入描述 第一行输入一个整数N(3≤N≤50)。 第二行…...

QT操作excel的两种方式 QT基础入门【Excel的操作】
QT操作excel的方式有两种:QAxObject 和QtXlsx QAxObject是通过调用office或者wps组件来实现对excel图表的操作的。只有装office软件或者wps软件就可以实现,但是 如果只装了office软件,有时可以用有时不可以用;如果只装wps软件&a…...
)
c++ qt--QString,弹出框(第二部分)
c qt–QString,弹出框(第二部分) 一.QString 1.所用头文件 #include<QString>2.功能 1.初始化 可以用字符,常量字符串、字符指针、字符数组等类型给QString进行初始化 QString str2"4567";//进行初始化2.拼…...

CSS自学框架之动画
这一节,自学CSS动画。主要学习了淡入淡出、淡入缩放、缩放、移动、旋转动画效果。先看一下成果。 优雅的过渡动画,为你的页面添加另一份趣味! 在你的选择器里插入 animation 属性,并添加框架内置的 keyframes 即可实现࿰…...

RabbitMQ的5种消息队列
RabbitMQ的5种消息队列 1、七种模式介绍与应用场景 1.1 简单模式(Hello World) 一个生产者对应一个消费者,RabbitMQ 相当于一个消息代理,负责将 A 的消息转发给 B。 应用场景:将发送的电子邮件放到消息队列,然后邮件服务在队列…...

【C语言】选择排序
基本原理 先找到数组中最大的那个数,将最大的数放到数组最右端(交换a[maxid]和a[len-1]这两个数的位置),然后继续从a[0]到a[len-2]中找到最大的数,然后交换a[maxid]和a[len-2]位置,依次查找交换,…...

异步更新队列 - Vue2 响应式
前言 这篇文章分析了 Vue 更新过程中使用的异步更新队列的相关代码。通过对异步更新队列的研究和学习,加深对 Vue 更新机制的理解 什么是异步更新队列 先看看下面的例子: <div id"app"><div id"div" v-if"isShow&…...
_抗锯齿(附带下载链接)】)
【Unity的URP渲染管线下实现扩展后处理Volume组件_TemporalAntiAliasing(TAA)_抗锯齿(附带下载链接)】
【Unity的URP渲染管线下的TAA抗锯齿】 背景:1. Unity内置的抗锯齿只能够满足部分画面需求。展示一个锯齿示例。2. 在75寸大屏电视上跑通展示一个锯齿示例。- 在Camera上配置3. 安装了一个TAA组建,最后打包APK在安卓机上运行报错。- 经过测试排查,发现是没有将后处理的shader…...
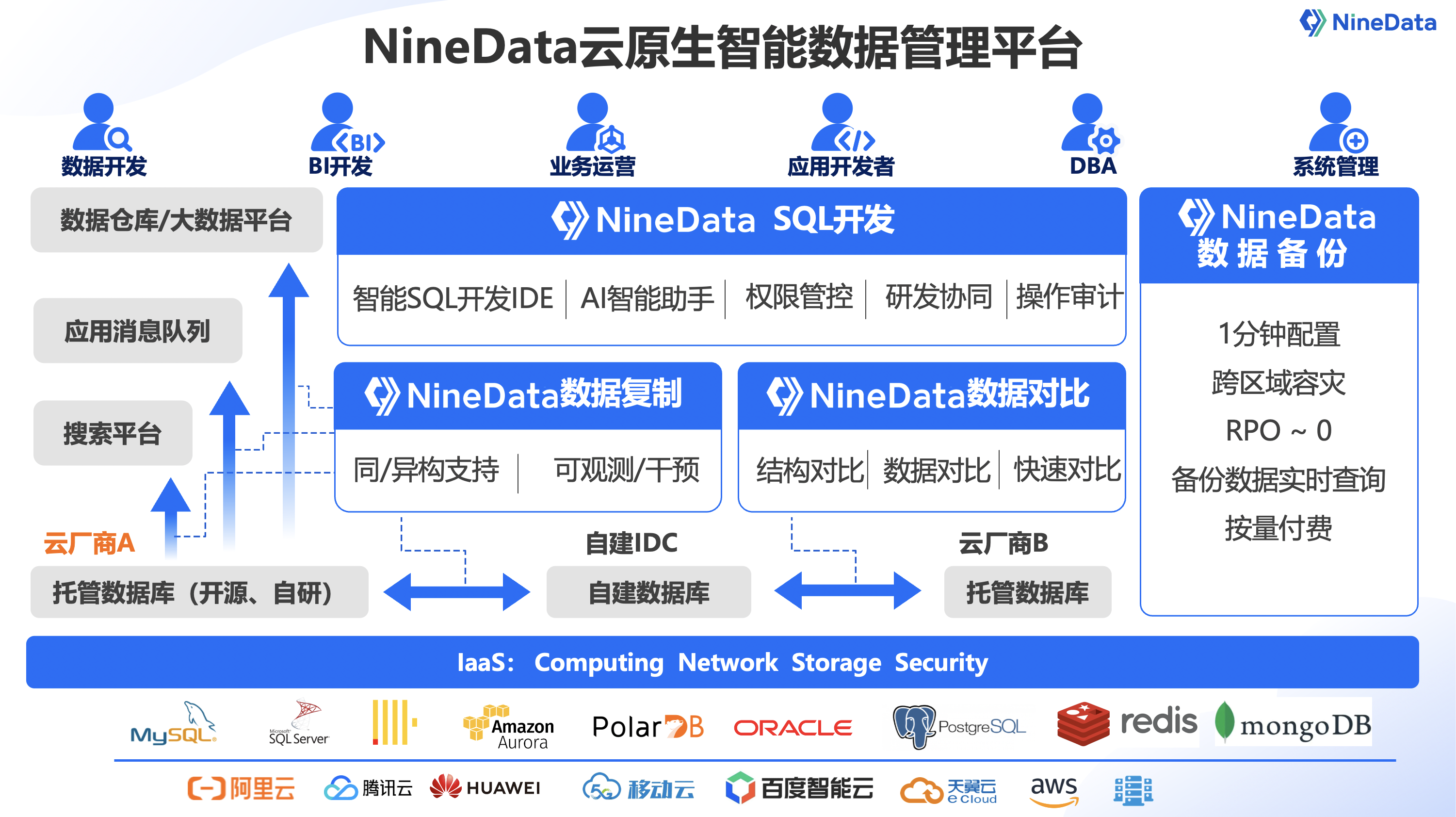
NineData通过AWS FTR认证,打造安全可靠的数据管理平台
近日,NineData 作为新一代的云原生智能数据管理平台,成功通过了 AWS(Amazon Web Service)的 FTR 认证。NineData 在 FTR 认证过程中表现出色,成功通过了各项严格的测试和评估,在数据安全管理、技术应用、流…...

Qt应用开发(基础篇)——滚屏区域类 QScrollArea
一、前言 QScrollArea类继承于QAbstractScrollArea,QAbstractScrollArea继承于QFrame,是Qt滚动视图的常用部件。 滚屏区域基类 QAbstractScrollArea 框架类 QFrame QScrollArea类提供了对另一个小部件的滚动视图,基础功能、滚动条控制、界面策…...
安装最新版chromedriver 116,亲测可用
Version Selection...

html题库
什么是HTML? HTML的全称为 超文本标记语言 ,是一种 标记语言 。 它包括一系列标签 ,通过这些标签可以将网络上的文档格式统一,使分散的 Internet 资源连接为一个逻辑整体。 DOCTYPE 的作用是什么?标准模式与兼容模式(…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...
