假设检验选择统计量重点-----正态总体参数的假设检验
文章目录
- 单个正态总体参数的假设检验
- 单边检验简介--计算拒绝域
- 两个正态总体参数的假设检验
- 方差已知的两正态总体均值的假设检验
- 均值未知的两正态总体方差的假设检验
单个正态总体参数的假设检验
- 设总体X∼N(μ,σ2)X\sim N(\mu,\sigma^2)X∼N(μ,σ2)
- X1,X2,⋯,XnX_1,X_2,\cdots,X_nX1,X2,⋯,Xn是来自XXX的样本
- 样本均值与样本方差为X‾,S2\overline{X},S^2X,S2
单个正态总体N(μ,σ2)N(\mu,\sigma^2)N(μ,σ2)的均值μ\muμ的假设检验
此时有两种情况:
- 1.σ2\sigma^2σ2已知(U检验法)
- 2.σ2\sigma^2σ2未知(t检验法)
1.σ2\sigma^2σ2已知(U检验法)
- 关于双边检验:H0:μ=μ0,H1:μ≠μ0H_0:\mu=\mu_0,H_1:\mu\ne\mu_0H0:μ=μ0,H1:μ=μ0
- U检验法的检验统计量为:U=X‾−μ0σ/n∼N(0,1)U=\frac{\overline X - \mu_0}{\sigma/\sqrt{n}}\sim N(0,1)U=σ/nX−μ0∼N(0,1)
- 知识点:对给定的α\alphaα,μ\muμ的置信度为1−α1-\alpha1−α的置信区间计算过程为:P(∣X‾−μσ/n∣<zα2)=1−αP(|\frac{\overline X - \mu}{\sigma/\sqrt{n}}|<z_{\frac{\alpha}2})=1-\alphaP(∣σ/nX−μ∣<z2α)=1−α
- 即P(X‾−σnzα2<μ<X‾+σnzα2)=1−αP(\overline X-\frac{\sigma}{\sqrt n}z_{\frac{\alpha}2}<\mu<\overline X+\frac{\sigma}{\sqrt n}z_{\frac{\alpha}2})=1-\alphaP(X−nσz2α<μ<X+nσz2α)=1−α
- 所以总体均值μ\muμ的置信度为1−α1-\alpha1−α的置信区间为(X‾−σnzα2,X‾+σnzα2)(\overline X-\frac{\sigma}{\sqrt n}z_{\frac{\alpha}2},\overline X+\frac{\sigma}{\sqrt n}z_{\frac{\alpha}2})(X−nσz2α,X+nσz2α)
- so,回答这个标题下的问题,H0H_0H0的拒绝域应该为(−∞,X‾−σnzα2)∪(X‾+σnzα2,+∞)(-\infty,\overline X-\frac{\sigma}{\sqrt n}z_{\frac{\alpha}2})\cup(\overline X+\frac{\sigma}{\sqrt n}z_{\frac{\alpha}2},+\infty)(−∞,X−nσz2α)∪(X+nσz2α,+∞)
单个正态总体方差的假设检验
单边检验简介–计算拒绝域
两个正态总体参数的假设检验
方差已知的两正态总体均值的假设检验
均值未知的两正态总体方差的假设检验
相关文章:

假设检验选择统计量重点-----正态总体参数的假设检验
文章目录单个正态总体参数的假设检验单个正态总体N(μ,σ2)N(\mu,\sigma^2)N(μ,σ2)的均值μ\muμ的假设检验1.σ2\sigma^2σ2已知(U检验法)单个正态总体方差的假设检验单边检验简介--计算拒绝域两个正态总体参数的假设检验方差已知的两正态总体均值的假设检验均值未知的两正态…...
 | 机试题算法思路 【2023】)
华为OD机试 - 通信误码(Python) | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 自动曝光(Python) | 机试题算法思路 【2023】 华为OD机试 - 双十一(Python) | 机试题算法思路 【2023】 华为OD机试 - 删除最少字符(Python) | 机试题算法思路 【2023-02】 华为OD机试 - Excel 单元格数值统计(Python) | 机试题算法思路 …...

设计模式之装饰者模式
文章の目录一、什么是装饰者模式二、优势三、缺点四、应用场景五、示例参考写在最后一、什么是装饰者模式 装饰者模式也称为包装器模式,在不改变原有对象的基础上为其动态的添加上新的功能。 装饰者模式有以下特点: 添加功能时不改变原对象结构。装饰…...
【第31天】SQL进阶-写优化- 插入优化(SQL 小虚竹)
回城传送–》《31天SQL筑基》 文章目录零、前言一、练习题目二、SQL思路:SQL进阶-写优化-插入优化解法插入优化禁用索引语法如下适用数据库引擎非空表:禁用索引禁用唯一性检查语法如下适用数据库引擎禁用外键检查语法如下适用数据库引擎批量插入数据语法…...
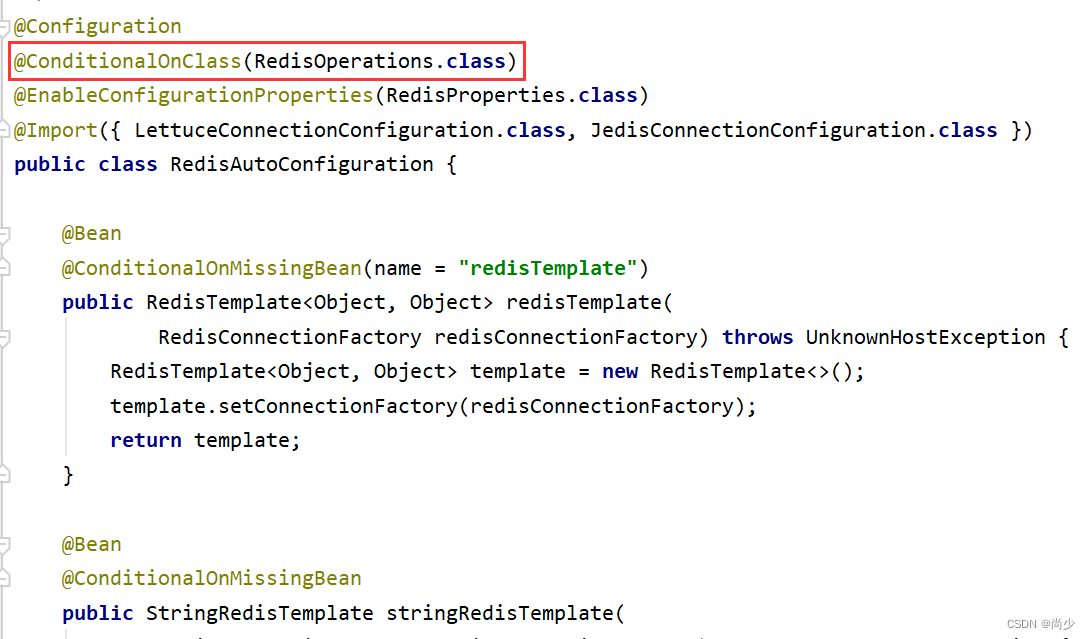
SpringBoot自动装配的原理
前言 在开发SpringBoot项目时,当我们引入spring-boot-starter-xxx依赖后,想要使用依赖中的bean,直接就用Autowired拿来用了,不需要用xml或者注解的方式把它先注入到Spring容器中。这就是自动装配的特性,本文来讲述Spri…...
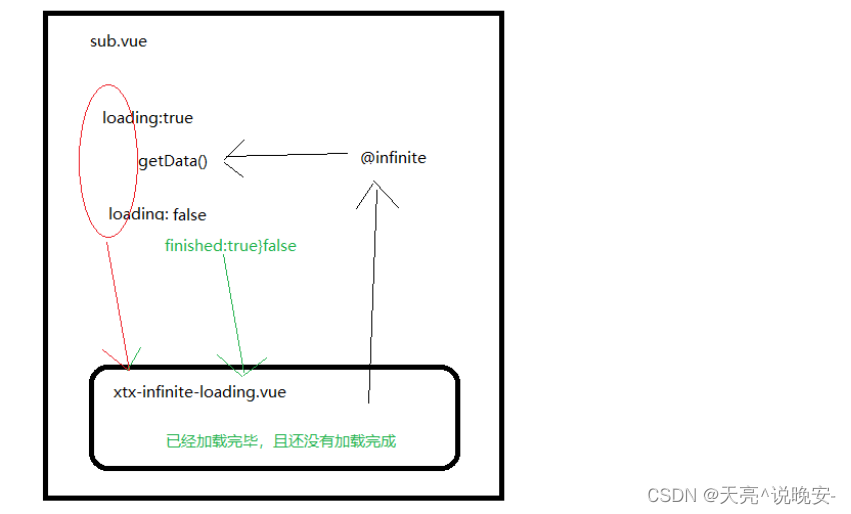
Vue3电商项目实战-分类模块5【12-二级类目-结果区-排序组件、13-二级类目-结果区-数据加载、14-二级类目-结果区-进行筛选】
文章目录12-二级类目-结果区-排序组件13-二级类目-结果区-数据加载14-二级类目-结果区-进行筛选12-二级类目-结果区-排序组件 目的:封装排序组件,完成排序切换效果 大致步骤: 定义一个组件 sub-sort,完成基础布局在 sub.vue 组件…...

计算机操作系统概述
文章目录1.0 操作系统概述1.1 操作系统的目标1.2 操作系统的功能1.3 操作系统结构1.4 操作系统接口1.5 操作系统的发展1.6 操作系统的特征2.0 进程管理2.1 进程调度2.2 进程调度算法2.3 进程间通信2.4 进程间的同步2.5 软件实现互斥的方法2.6 硬件实现互斥的方法2.7 信号2.8 管…...
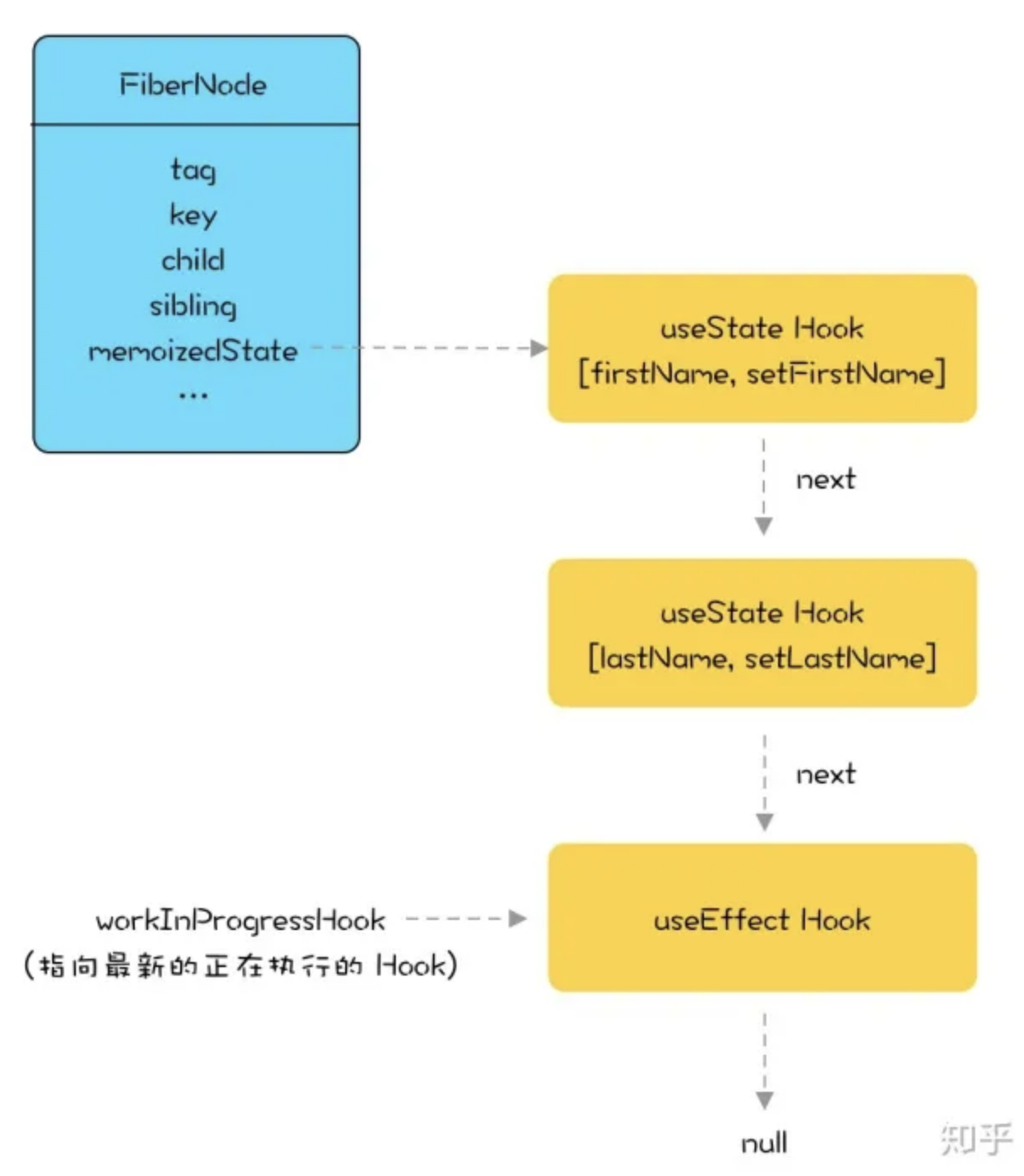
面试官让你说说react状态管理?
hooks 为什么不能放在条件判断里 以 setState 为例,在 react 内部,每个组件(Fiber)的 hooks 都是以链表的形式存在 memoizeState 属性中 update 阶段,每次调用 setState,链表就会执行 next 向后移动一步。如果将 setState 写在条…...

CUDA线程块的分配
为了确保能够真正地了解线程块的分配,接下来我们写一个简短的内核程序来输出线程块、线程、线程束和线程全局标号到屏幕上。现在,除非你使用的是 3.2 版本以上的 SDK否则内核中是不支持 printf的。因此,我们可以将数据传送回 CPU 端然后输出到…...
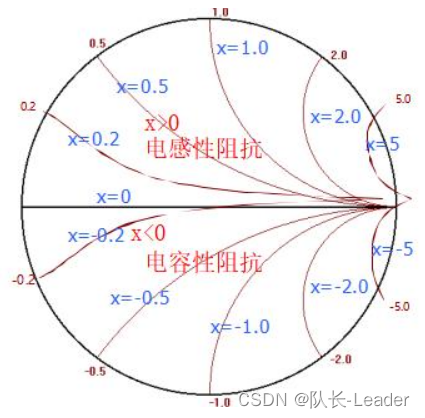
史密斯圆图
在射频、微波中,常常使用史密斯圆图来做阻抗匹配。在不涉及复杂的数学推导,仍能把圆图用起来。 比如,共轭匹配。 RL1jX,需要找到-jX来抵消jX,消掉虚部之后,只留下实部,最终等效为RL‘1。 史密…...
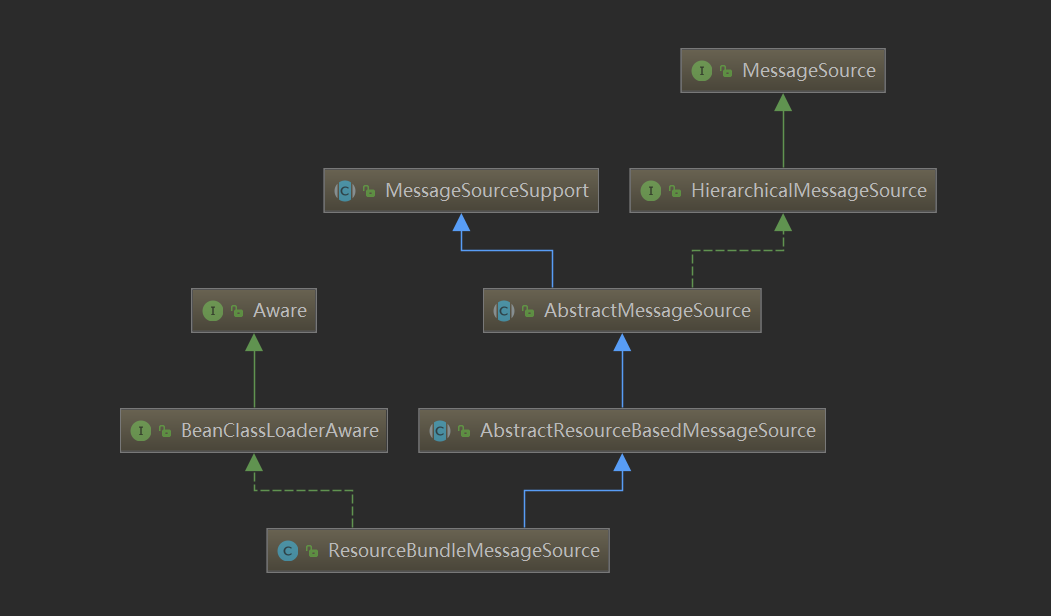
Spring国际化实现
Java国际化 Java使用Unicode来处理所有字符。 Locales 国际化主要涉及的是数字、日期、金额等。 有若干个专门负责格式处理的类。为了对格式进行控制,可以使用Locale类。它描述了: 一种语言一个位置(通常包含)一段脚本(可选,自Java SE7开…...
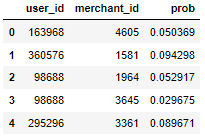
10- 天猫用户复购预测 (机器学习集成算法) (项目十) *
项目难点 merchant: 商人重命名列名: user_log.rename(columns{seller_id:merchant_id}, inplaceTrue)数据类型转换: user_log[item_id] user_log[item_id].astype(int32)主要使用方法: xgboost, lightbm竞赛地址: 天猫复购预测之挑战Baseline_学习赛_天池大赛-阿里云天池…...

对于《MySQL 实战45讲》的理解
一.理论 一条SQL执行过程 连接器分析器优化器执行器 索引 索引的出现其实就是为了提高数据查询的效率,就像书的目录一样 常见索引数据结构(每碰到一个新数据库,我们需要先关注它的数据模型,这样才能从理论上分析出这个数据库的适用场景) 哈希…...

XQuery 函数
XQuery 1.0、XPath 2.0 以及 XSLT 2.0 共享相同的函数库。 XQuery 函数 XQuery 含有超过 100 个内建的函数。这些函数可用于字符串值、数值、日期以及时间比较、节点和 QName 操作、序列操作、逻辑值等等。您也可在 XQuery 中定义自己的函数。 XQuery 内建函数 XQuery 函数命…...
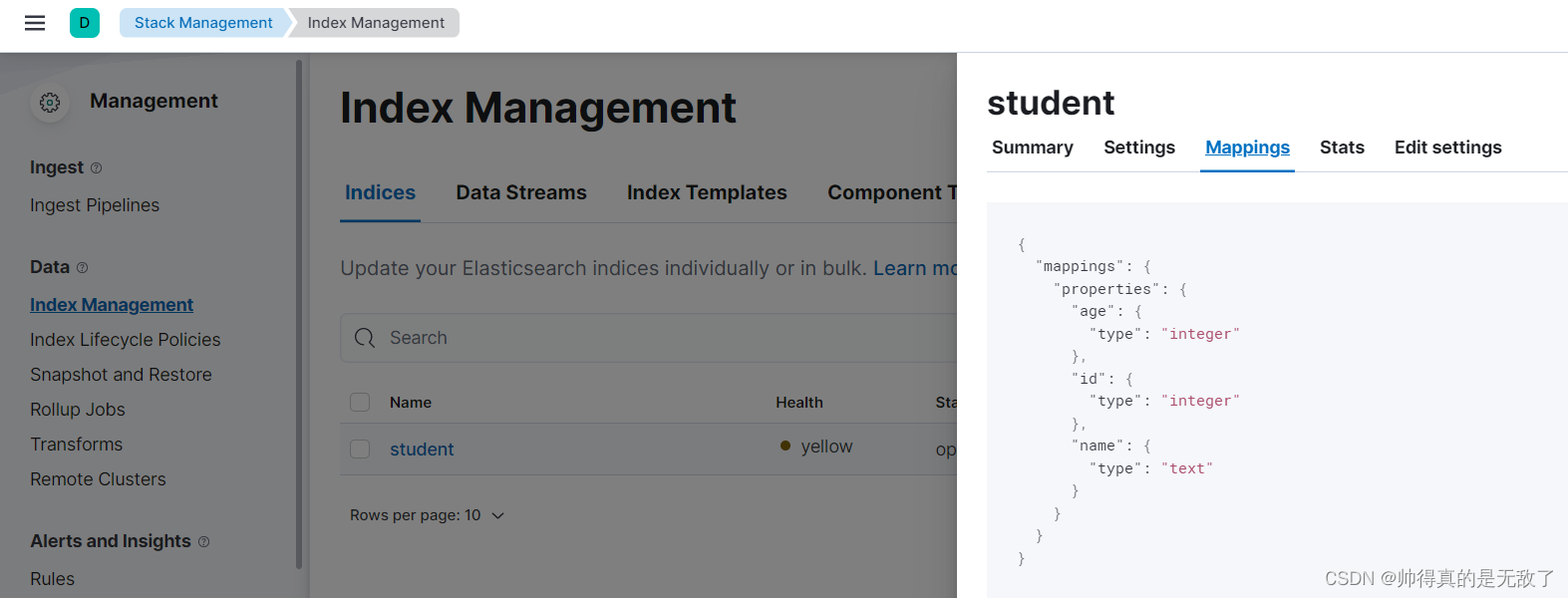
Elasticsearch的安装及常用操作
文章目录一、Elasticsearch的介绍1、Elasticsearch索引2、Elasticsearch的介绍二、Elasticsearch的安装1、安装ES服务2、安装kibana3、Docker安装ES4、Docker安装Kibana三、ES的常用操作1、索引操作2、文档操作3、域的属性3.1 index3.2 type3.3 store总结一、Elasticsearch的介…...
网络安全应急响应服务方案怎么写?包含哪些阶段?一文带你了解!
文章目录一、服务范围及流程1.1 服务范围1.2 服务流程及内容二、准备阶段2.1 负责人准备内容2.2 技术人员准备内容(一)服务需求界定(二)主机和网络设备安全初始化快照和备份2.3市场人员准备内容(1)预防和预…...

11、事务原理和实战,MVCC
事务原理和实战 1. 认识事务2. 事务控制语句2.1 开启事务2.2 事务提交2.3 事务回滚3. 事务的实现方式3.1 原子性3.2 一致性3.3 隔离性3.3 持久性4purge thread线程5事务统计QPS与TPS5.1 QPS5.2 TPS6. 事务隔离级别6.1 隔离级别6.2 查看隔离级别6.3 设置隔离级别6.4 不同隔离级别…...
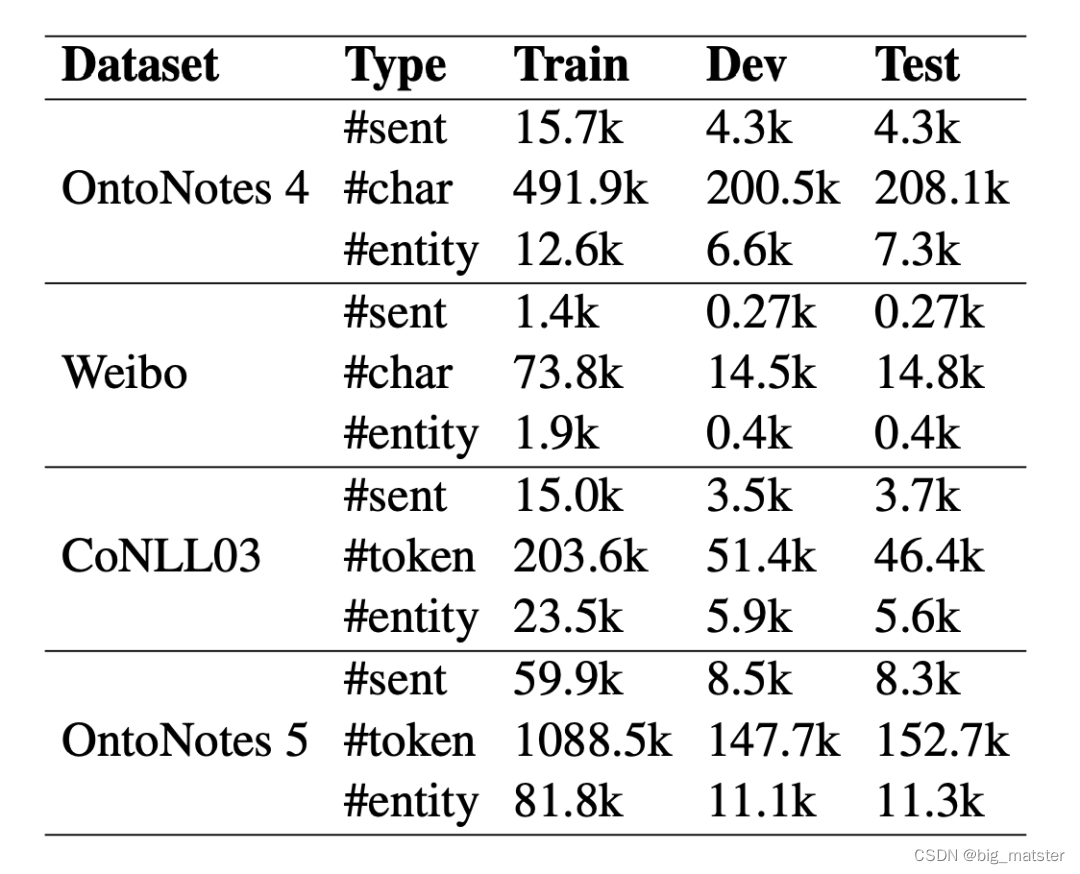
Robust Self-Augmentation for Named Entity Recognition with Meta Reweighting
摘要 近年来,自我增强成为在低资源场景下提升命名实体识别性能的研究热点。Token substitution and mixup (token替换和表征混合)是两种有效提升NER性能的自增强方法。明显,自增强方法得到的增强数据可能由潜在的噪声。先前的研究…...

Java基础-xml
1.xml 1.1概述 万维网联盟(W3C) 万维网联盟(W3C)创建于1994年,又称W3C理事会。1994年10月在麻省理工学院计算机科学实验室成立。 建立者: Tim Berners-Lee (蒂姆伯纳斯李)。 是Web技术领域最具权威和影响力的国际中立性技术标准机构。 到目前为止&#…...

TCP的Nagle算法和delayed ack---延时发送和延时应答与稍带应答选项
本文目录提高TCP的网络利用率的二个思考解决方案:Nagle算法和delayed ack(延时发送和延时应答与稍带应答选项)Nagle算法和delayed ack算法同时启动可能会导致的问题提高TCP的网络利用率的二个思考 我们都知道,TCP是一个基于字节流…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
