用于优化开关性能的集成异质结二极管的4H-SiC沟道MOSFET
标题:4H-SiC Trench MOSFET with Integrated Heterojunction Diode for Optimizing Switching Performance
摘要
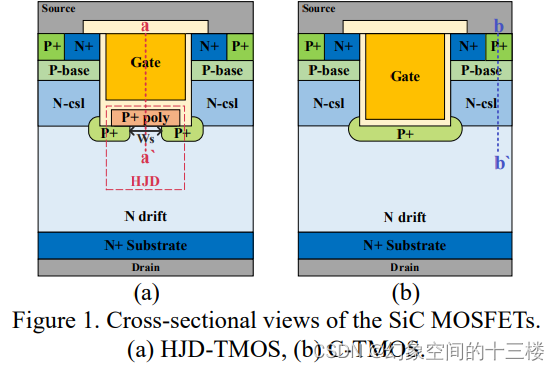
本研究提出了一种新型的4H-SiC沟道MOSFET,其在栅槽底部集成了异质结二极管(HJD-TMOS),并通过TCAD模拟进行了研究。集成的异质结二极管在反向导通中充当自由轮二极管,与传统的SiC沟道MOSFET(C-TMOS)相比,显著降低了反向恢复电荷(Qrr)和反向开启膝压(Von)超过2倍,同时几乎保持了相同的阈值电压和击穿电压。此外,由于栅下多晶硅的屏蔽效应,与C-TMOS相比,栅到漏电荷(Qgd)减少了68%。因此,HJD-TMOS是高频率、高效率应用的潜在选择。
文章研究了什么
- 该文章研究了一种新型的4H-SiC沟道MOSFET,其在栅槽底部集成了异质结二极管(HJD-TMOS)。
- 集成的异质结二极管在反向导通中充当自由轮二极管,与传统的SiC沟道MOSFET(C-TMOS)相比,显著降低了反向恢复电荷(Qrr)和反向开启膝压(Von),降幅超过2倍。
- HJD-TMOS通过减少栅和漏极之间的耦合效应,改善了开关特性,从而降低了栅到漏电荷(Qgd)和总开关损耗。
- HJD-TMOS在第三象限表现出卓越的性能,具有较低的Von和Qrr,更快的反向电流处理,减少的死时间,并且有效降低了开关损耗。
- HJD-TMOS中集成的HJD有效抑制了少数载流子向漂移区的注入,优化了反向恢复特性并抑制了双极降解。
文章的创新点
- 该文章的创新点在于提出并研究了一种新型的4H-SiC沟道MOSFET,其在栅槽底部集成了异质结二极管(HJD-TMOS)。
- 集成的异质结二极管在反向导通中充当自由轮二极管,与传统的SiC沟道MOSFET(C-TMOS)相比,显著降低了反向恢复电荷(Qrr)和反向开启膝压(Von)。
- HJD-TMOS通过减少栅和漏极之间的耦合效应,改善了开关特性,从而降低了栅到漏电荷(Qgd)和总开关损耗。
- HJD-TMOS中集成的HJD有效抑制了少数载流子向漂移区的注入,优化了反向恢复特性并抑制了双极降解。
文章的研究方法
该论文的研究方法主要基于TCAD模拟。作者通过TCAD模拟提出并研究了一种新型的4H-SiC沟道MOSFET,其在栅槽底部集成了异质结二极管(HJD-TMOS)。他们详细比较了HJD-TMOS与传统SiC沟道MOSFET(C-TMOS)的性能,分析了反向恢复电荷(Qrr)、反向开启膝压(Von)、栅到漏电荷(Qgd)和总开关损耗等参数。他们还分析了两种器件在正向和反向导通下的J-V曲线。此外,作者提供了插图和图表来支持其研究结果,例如空穴密度分布图和能带图。总体而言,该研究方法涉及基于模拟的分析,并对所提出的HJD-TMOS与传统的C-TMOS进行比较。
文章的结论
- 该论文的结论是,所提出的集成异质结二极管的4H-SiC沟道MOSFET(HJD-TMOS)在开关性能方面相较于传统的SiC沟道MOSFET(C-TMOS)有显著改进。
- HJD-TMOS中集成的异质结二极管使反向恢复电荷(Qrr)和反向开启膝压(Von)降低了2倍以上,同时保持了类似的阈值电压和击穿电压。
- HJD-TMOS还展示了较低的栅到漏电荷(Qgd)和总开关损耗,适用于高频率和高效率应用。
- HJD-TMOS有效地抑制了少数载流子向漂移区的注入,优化了反向恢复特性并抑制了双极降解。
- TCAD模拟结果支持HJD-TMOS在特定导通电阻降低、反向电流处理更快和开关特性改善等方面的优越性能。
相关文章:

用于优化开关性能的集成异质结二极管的4H-SiC沟道MOSFET
标题:4H-SiC Trench MOSFET with Integrated Heterojunction Diode for Optimizing Switching Performance 摘要 本研究提出了一种新型的4H-SiC沟道MOSFET,其在栅槽底部集成了异质结二极管(HJD-TMOS),并通过TCAD模拟进…...

优化个人博客总结
前面学习完怎么搭建个人博客,后面要做的就是排版优化自己的博客了,今天通过教程学习到了然后更爱美化其中的效果,还通过改写代码来带到基本的效果展示,同时也把最开始学习的计算速成课的笔记输出在上面,这也是一个很好…...
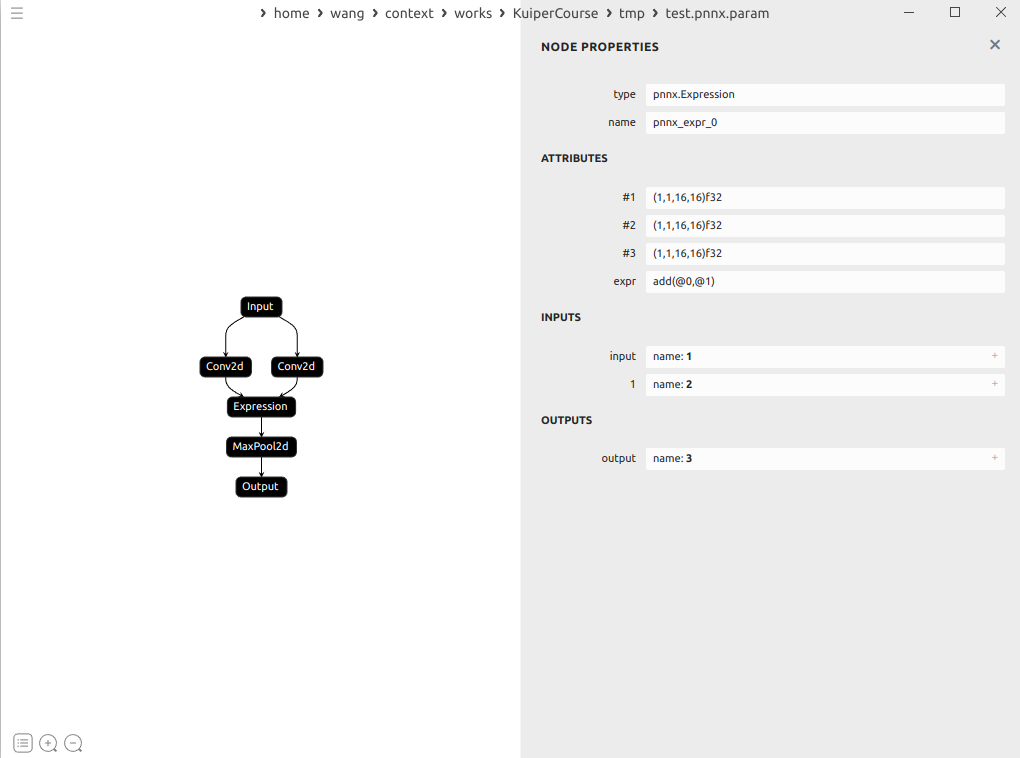
从零构建深度学习推理框架-9 再探Tensor类,算子输入输出的分配
再探Tensor类: 第二节中我们编写的Tensor类其实并不能满足我们的使用需要,我们将在这一节以代码阅读的方式来看看一个完全版本的Tensor应该具备怎样的要素,同时我们对Tensor类的分析来看看在C中一个设计好的类应该是怎么样的。 Tensor<fl…...

Vue使用element-ui
main.js配置 //引入Vue import Vue from vue //引入App import App from ./App.vue//完整引入 //引入ElementUI组件库 // import ElementUI from element-ui; //引入ElementUI全部样式 // import element-ui/lib/theme-chalk/index.css;//按需引入 import { Button,Row,DatePi…...

使用ApplicationRunner简化Spring Boot应用程序的初始化和启动
ApplicationRunner这个接口,我们一起来了解这个组件,并简单使用它吧。🤭 引言 在开发Spring Boot应用程序时,应用程序的初始化和启动是一个重要的环节。ApplicationRunner是Spring Boot提供的一个有用的接口,可以帮助…...

Vue 2.x 项目升级到 Vue 3详细指南【修改清单】
文章目录 前言0.迁移过程1. 安装 Vue 32. 逐一处理迁移中的警告3. 迁移全局和内部 API4. 迁移 Vue Router 和 Vuex5. 处理其他的不兼容变更 1. Vue3特性1. Composition API2. 更好的性能3. 更好的 TypeScript 支持4. 多个根元素5. Suspense 组件6. Teleport 组件7. 全局 API 的…...

【算法日志】贪心算法刷题:重叠区问题(day31)
代码随想录刷题60Day 目录 前言 无重叠区间(筛选区间) 划分字母区间(切割区间) 合并区间 前言 今日的重点是掌握重叠区问题。 无重叠区间(筛选区间) int eraseOverlapIntervals(vector<vector<in…...
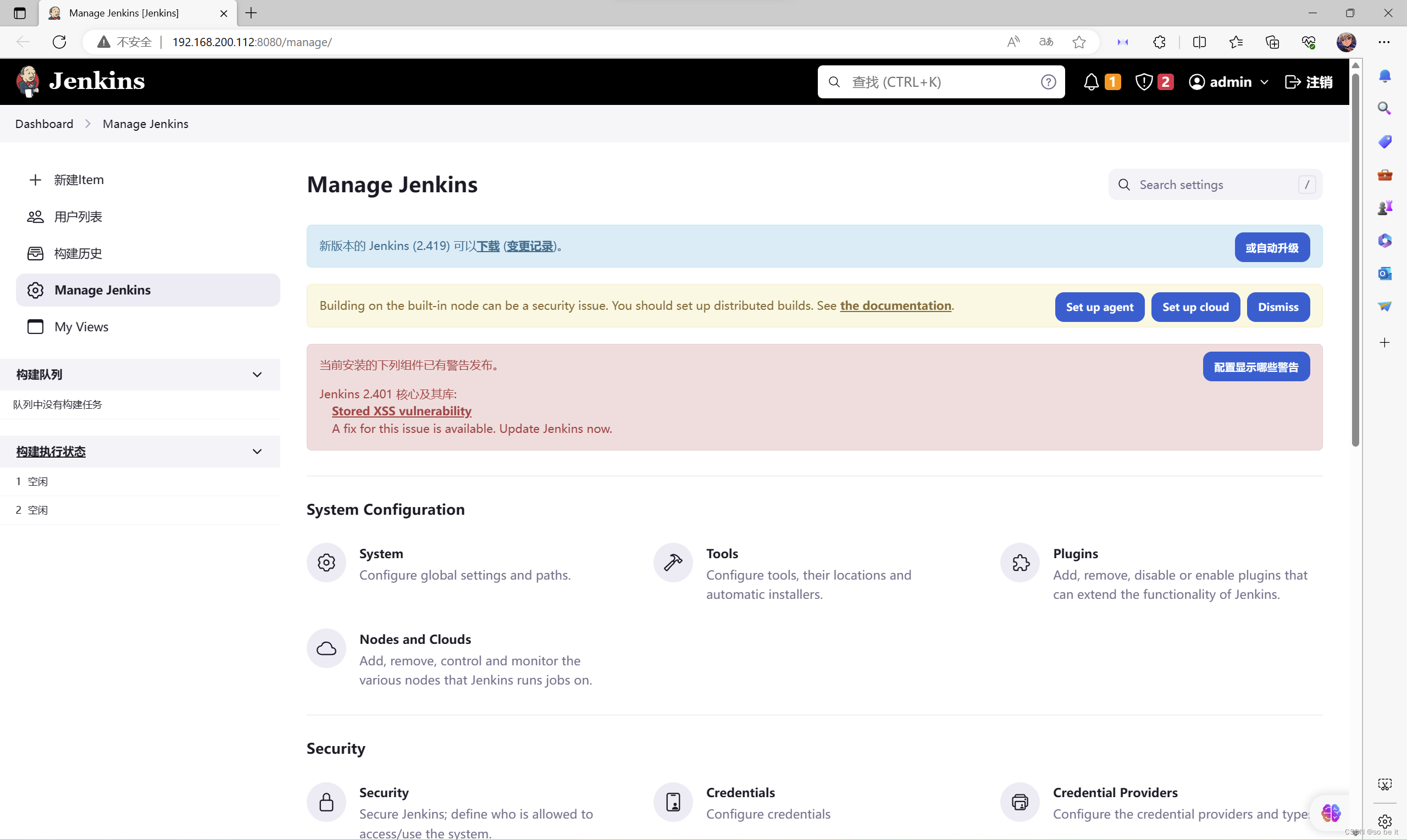
基于Jenkins构建生产CICD环境、jenkins安装
目录 Jenkins简介 安装配置Jenkins Jenkins简介 Jenkins是一个用Java编写的开源的持续集成工具。在与Oracle发生争执后,项目从Hudson项目独立。官方网站:https://jenkins.io/。 Jenkins提供了软件开发的持续集成服务。它运行在Servlet容器中ÿ…...
基于Java SpringBoot+vue+html 的地方美食系统(2.0版本)
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝30W,csdn、博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 文章目录 1 简介2 技术栈3 系统流程的分析3.1 用户管理的流程3.2个人中心管理流程3.3登录流程 4系统设计…...
opencv-gpu版本编译(添加java支持,可选)实现硬解码
目录 opencv gpu版本编译,实现硬解码,加速rtsp视频流读取1、准备文件2、复制 NVCUVID 头文件到 cuda 安装目录 include3、安装相关依赖4、 执行cmake5、编译安装6、测试 opencv gpu版本编译,实现硬解码,加速rtsp视频流读取 前置条…...
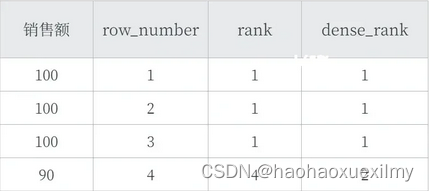
数据分析问答总结
一、SQL窗口函数 1.是什么 OLAP(Online Anallytical Processing联机分析处理),对数据库数据进行实时分析处理。 2.基本语法: <窗口函数>OVER (PARTITION BY <用于分组的列名> ORDER BY <用于排序的…...
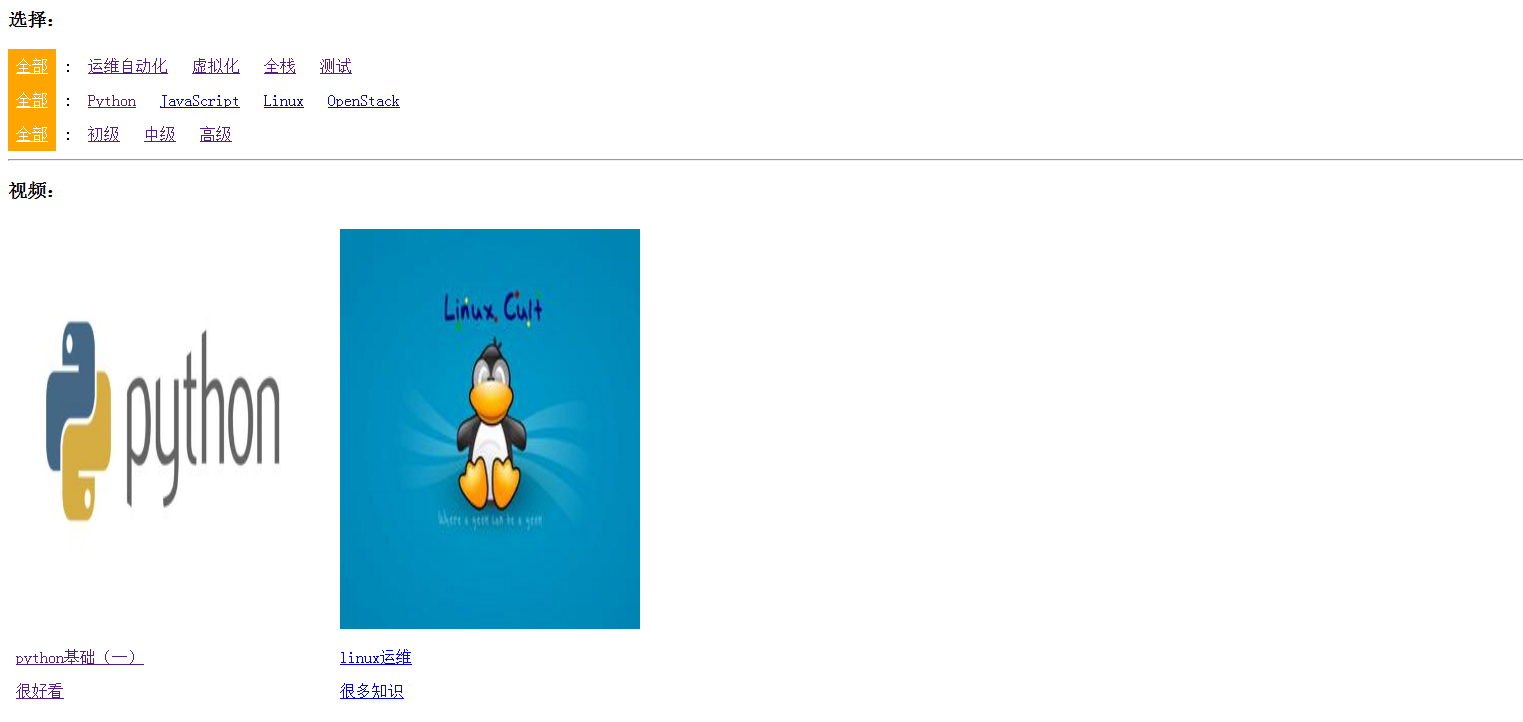
Python学习笔记_实战篇(二)_django多条件筛选搜索
多条件搜索在很多网站上都有用到,比如京东,淘宝,51cto,等等好多购物教育网站上都有,当然网上也有很多开源的比楼主写的好的多了去了,仅供参考,哈哈 先来一张效果图吧,不然幻想不出来…...

【生态经济学】利用R语言进行经济学研究技术——从数据的收集与清洗、综合建模评价、数据的分析与可视化、因果推断等方面入手
查看原文>>>如何快速掌握利用R语言进行经济学研究技术——从数据的收集与清洗、综合建模评价、数据的分析与可视化、因果推断等方面入手 近年来,人工智能领域已经取得突破性进展,对经济社会各个领域都产生了重大影响,结合了统计学、…...

xml中的vo是干什么用的
在Java中,VO(Value Object)是一种常见的设计模式,用于表示纯粹的数据对象。VO 通常用于在不同层或模块之间传递数据,并且它们的主要目的是封装和组织数据,而不包含业务逻辑。 VO 在Java中的具体作用有以下…...

现代企业数据泄露的原因分析与建议
近年来,随着信息技术的飞速发展,数据已经成为现代企业不可或缺的发展资源。然而,随之而来的数据泄露危机,给个人、企业甚至整个社会带来了巨大的风险与威胁。本文将综合探讨企业数据泄露的主要途径和原因,并提出防护建…...
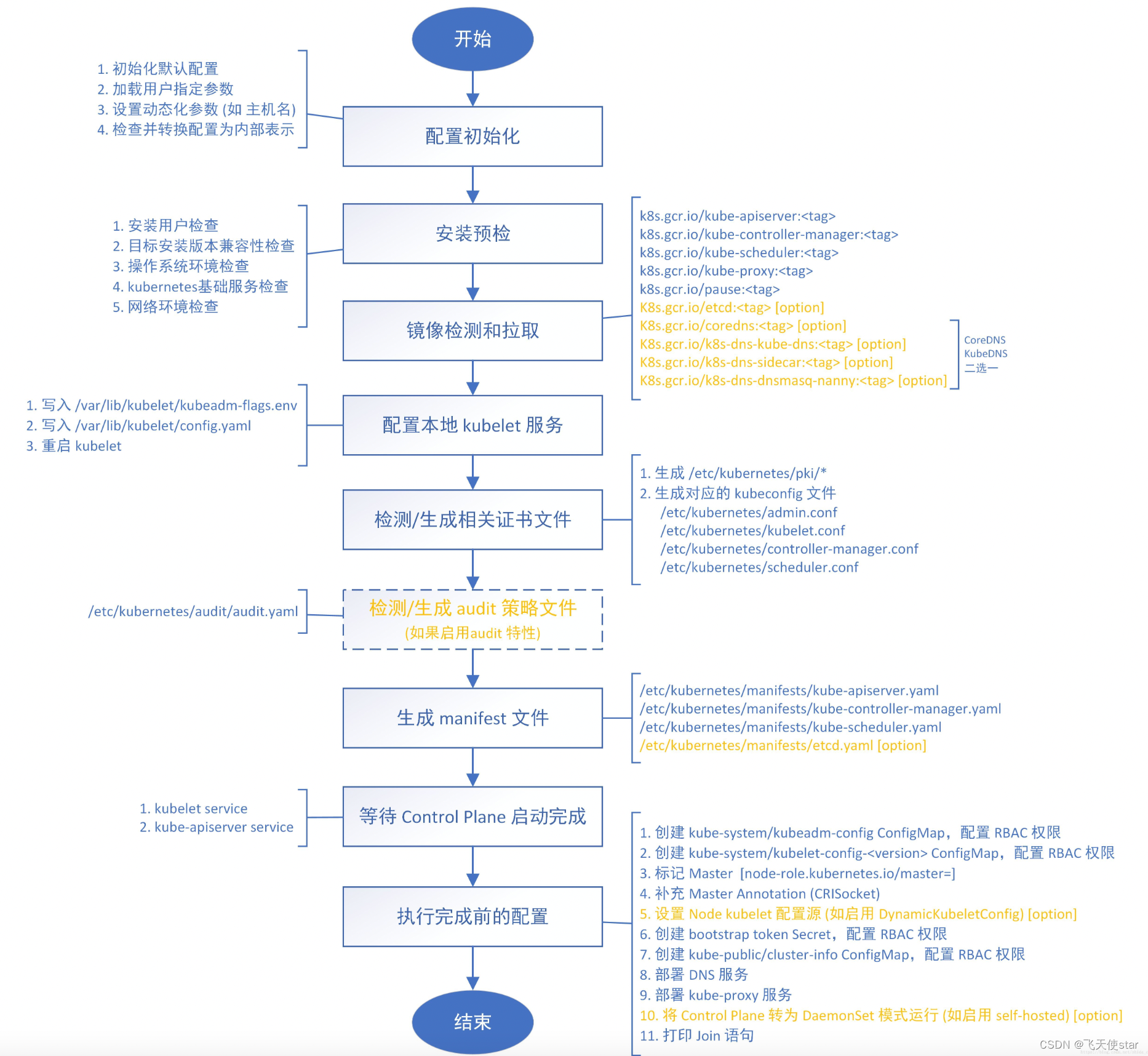
飞天使-kubeadm安装一主一从集群
文章目录 安装前准备安装前准备配置yum源等安装前准备docker安装 安装kubeadm配置kubeadm验证集群 参考链接 安装前准备 cat >> /etc/hosts <<EOF 192.168.100.30 k8s-01 192.168.100.31 k8s-02 EOF hostnamectl set-hostname k8s-01 #所有机器按照要求修改 ho…...

string类写时拷贝
文章目录 1.string类拷贝构造函数的现代写法2.string类写时拷贝vs和g下string结构的不同vs下string的结构:g下string的结构 3.总结 1.string类拷贝构造函数的现代写法 string类拷贝构造函数的传统写法: string(const string& s){if (this ! &s)…...
QT VS编译环境无法打开包括文件type_traits
这问题,别人给的处理方法都是: 添加环境变量执行vsvars32.bat/vcvarsall.bat/vsdevcmd.bat重新安装QT项目:执行qmake。。。。 个人不推荐配置环境编译,除非你非常熟,因为配置环境变量需要你知道有哪些路径需要添加&a…...
深入浅出 TCP/IP 协议栈
TCP/IP 协议栈是一系列网络协议的总和,是构成网络通信的核心骨架,它定义了电子设备如何连入因特网,以及数据如何在它们之间进行传输。TCP/IP 协议采用4层结构,分别是应用层、传输层、网络层和链路层,每一层都呼叫它的下…...

Servlet+JDBC实战开发书店项目讲解第13讲:库存管理功能
ServletJDBC实战开发书店项目讲解第13讲:库存管理功能 在第13讲中,我们将讲解如何实现书店项目中的库存管理功能。该功能包括图书的添加、编辑、删除和查询等核心功能。下面是实现该功能的主要思路: 显示库存列表: 创建一个管理页…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
