课程表-广度优先和图
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
例如,先修课程对 [0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:true
解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
示例 2:输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
输出:false
解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。提示:
1 <= numCourses <= 1 0 5 10^5 105
0 <= prerequisites.length <= 5000
prerequisites[i].length == 2
0 <= ai, bi < numCourses
prerequisites[i] 中的所有课程对 互不相同
该题目涉及到图
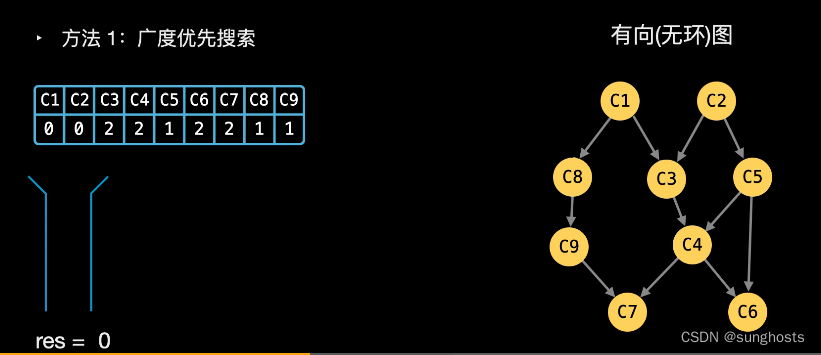
用一个数组记录每门课程的先导课程,总有没有先导课程的课程,先访问这些课程,随后以这些课程为先导课程的课程减去访问过的先导课程,直到无法再访问课程,这时候根据访问过的课程数据是否是课程总数,决定结果。
这里用到两个数据结构,edges变量存放以该课程为先导课程的课程,访问先导课程后就知道哪些课程要减去访问过的课程。q是一个队列存放待访问的课程。
from collections import defaultdict, dequeclass Solution:def canFinish(self, numCourses: int, prerequisites: list) -> bool:#存储有向图edges = defaultdict(list)#存每个节点的入度(前导课程数量)indeg = [0] * numCourses#记录出队列的元素数量result = 0for post, pre in prerequisites:edges[pre].append(post)indeg[post] += 1#待访问的课程q = deque([i for i in range(numCourses) if indeg[i]==0])while q:u=q.popleft()result += 1for v in edges[u]:indeg[v] -= 1if indeg[v] == 0:q.append(v)return result == numCourses
相关文章:

课程表-广度优先和图
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。 在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。 例如&am…...
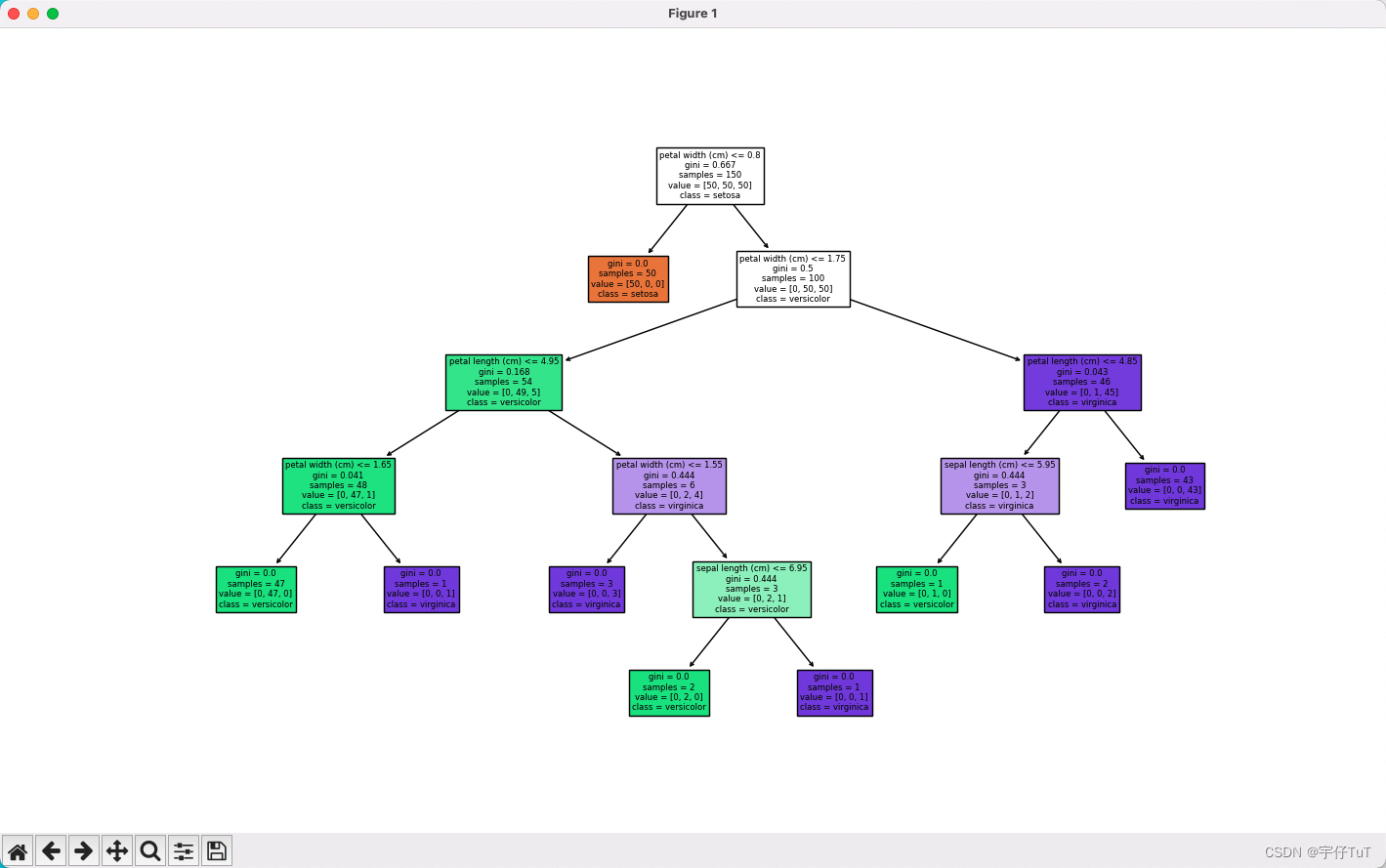
机器学习|决策树:数学原理及代码解析
机器学习|决策树:数学原理及代码解析 决策树是一种常用的监督学习算法,适用于解决分类和回归问题。在本文中,我们将深入探讨决策树的数学原理,并提供 Python 示例代码帮助读者更好地理解和实现该算法。 决策树数学原…...
1.0的星火2.0必将燎原——图文声影PPT全测试
一、前言 大家好,勇哥又来分享AI模型了,前几天讯飞发布的星火大模型2.0迅速的进入了我们圈子里,为了有更多更好的模型分享给大家,分享星火大模型2.0是必须做的,我做一个传递着,希望大家也星火相传啊。 我…...
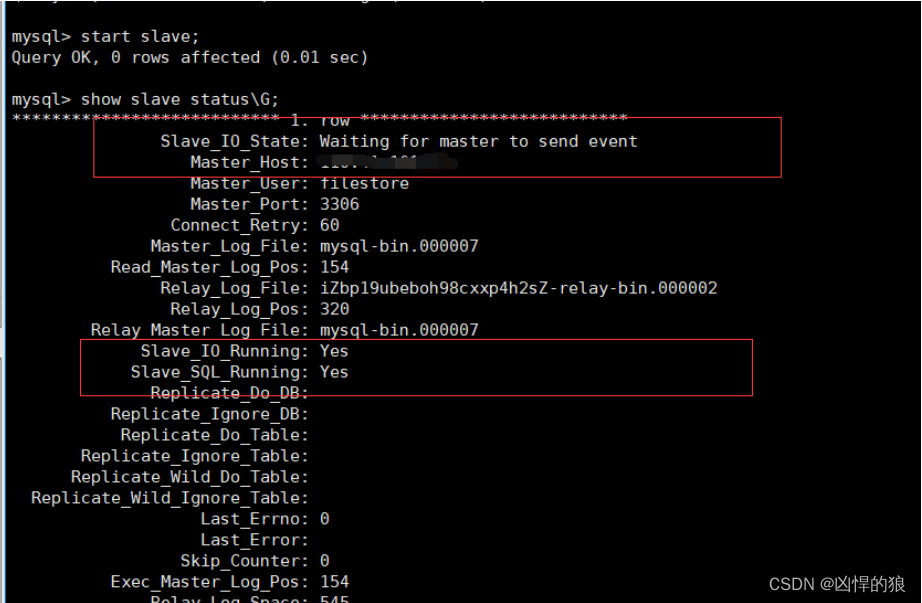
[MySQL]主从服务器布置
配置主服务器 配置文件 /etc/my.cnf 在[mysqld]下进行配置 log_binON //启动二进制日志 log-bin mysql-bin //启用二进制日志,用于记录主服务器的更新操作 server-id 1 // 用来表示mysql服务id,保证集成环境中的唯一性 , 范围 [1,2^32) read-only0 // 1表示只…...
----NV12转成I420,RGB24,ARGB集合)
图像处理算法大全(基于libyuv或IPP)----NV12转成I420,RGB24,ARGB集合
《周星星教你学ffmpeg》技巧 libyuv源码: static void NV12ToI420(BYTE* pNV12_Y, BYTE* pNV12_UV, BYTE* pYV12, int width, int height) { libyuv::NV12ToI420(pNV12_Y, width, pNV12_UV, width, pYV12, width, pYV12 height*width, width / 2, pYV12 hei…...
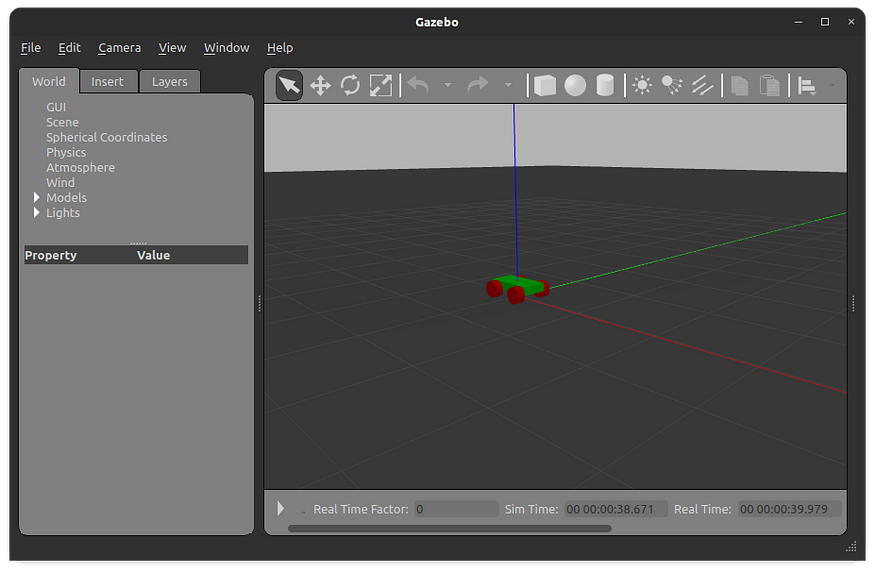
机器人操作系统:ROS2 仿真入门
塞巴斯蒂安 一、说明 在机器人项目中,仿真是一个具有多种用途的重要方面。首先,您可以测试希望机器人执行的行为代码。其次,您可以使用仿真来测试不同类型的硬件,例如距离传感器、相机或 3D 点云传感器,看看哪种效果最…...

面试题:线程池的底层工作原理
线程池的几个重要的参数: 1、corePoolSize:线程池的核心线程数(也是默认线程数) 2、maximumPoolSize:最大线程数 3、keepAliveTime:允许的线程最大空闲时间(单位/秒) 线程池内部是…...
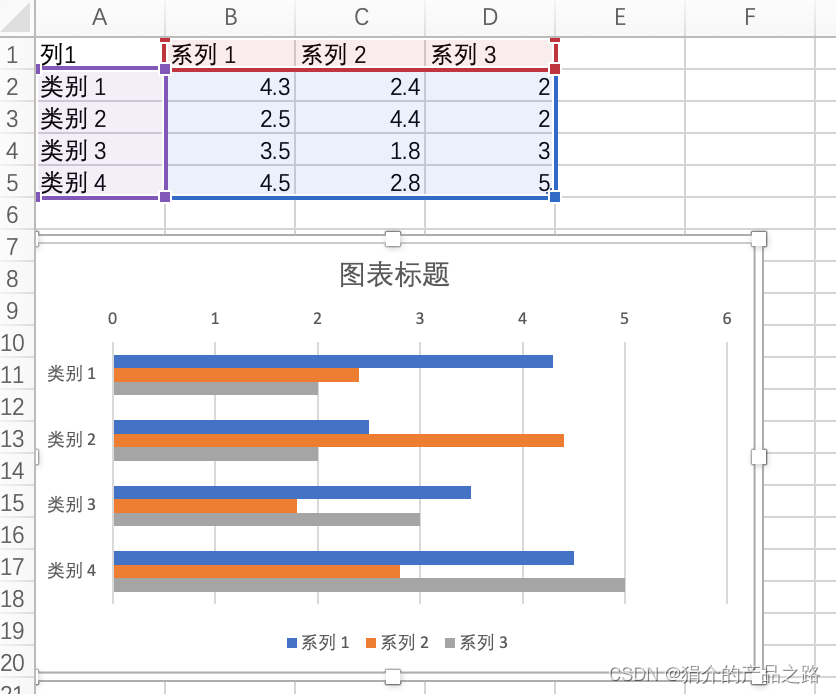
Excel/PowerPoint条形图改变顺序
条形图是从下往上排的,很多时候不是我们想要的效果 解决方案 选择坐标轴,双击,按下图顺序点击 效果...
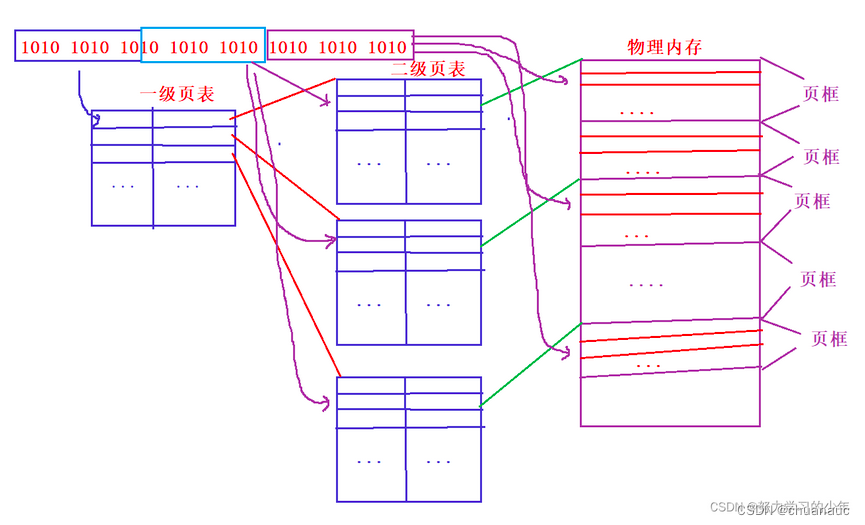
【操作系统】虚拟内存相关分段分页页面置换算法
虚拟内存是什么? 【进程地址空间虚拟地址空间C/C程序地址空间就是那个4G的空间】 虚拟内存是操作系统内核为了对进程地址空间进行管理,而设计的一个逻辑意义上的内存空间概念。在程序运行过程中,虚拟内存中需要被访问的部分会被映射到物理内…...

Unrecognized Hadoop major version number: 3.0.0-cdh6.3.2
一.环境描述 spark提交job到yarn报错,业务代码比较简单,通过接口调用获取数据,将数据通过sparksql将数据写入hive中,尝试各种替换hadoop版本,最后拿下 1.hadoop环境 2.项目 pom.xml spark-submit \ --name GridCorr…...

机器学习分类,损失函数中为什么要用Log,机器学习的应用
目录 损失函数中为什么要用Log 为什么对数可以将乘法转化为加法? 机器学习(Machine Learning) 机器学习的分类 监督学习 无监督学习 强化学习 机器学习的应用 应用举例:猫狗分类 1. 现实问题抽象为数学问题 2. 数据准备…...
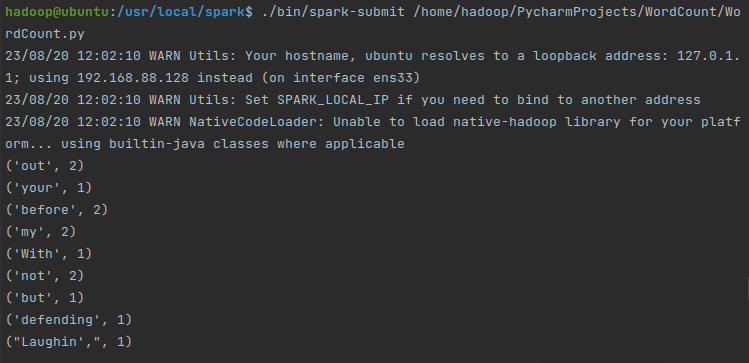
PySpark安装及WordCount实现(基于Ubuntu)
先盘点一下要安装哪些东西: VMwareubuntu 14.04(64位)Java环境(JDK 1.8)Hadoop 2.7.1Spark 2.4.0(Local模式)Pycharm (一)Ubuntu VMware 和 ubuntu 14.04(…...
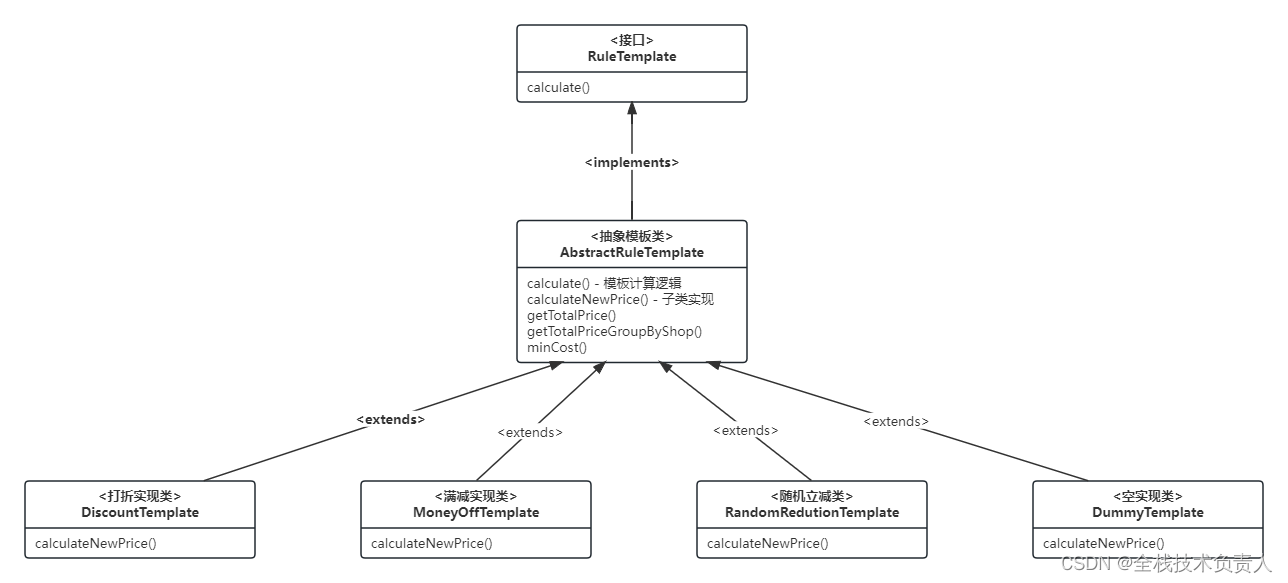
SpringBoot 模板模式实现优惠券逻辑
一、计算逻辑的类结构图 在这张图里,顶层接口 RuleTemplate 定义了 calculate 方法,抽象模板类 AbstractRuleTemplate 将通用的模板计算逻辑在 calculate 方法中实现,同时它还定义了一个抽象方法 calculateNewPrice 作为子类的扩展点。各个具…...
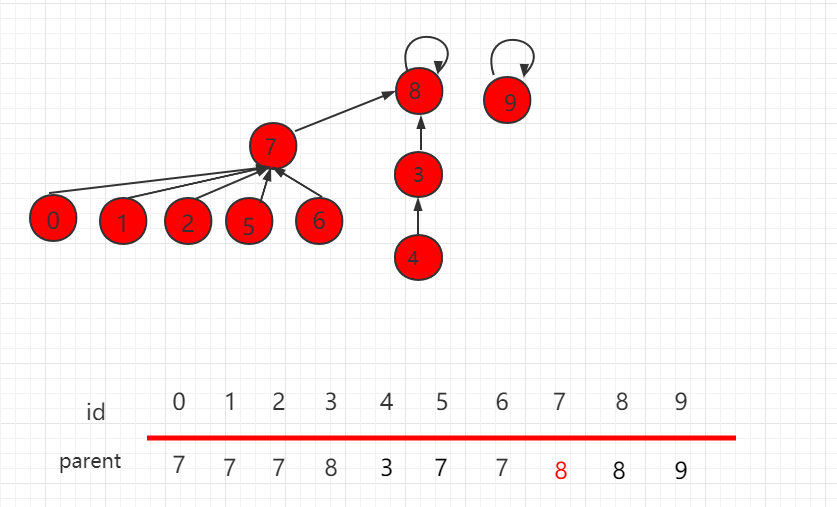
并查集 rank 的优化(Java 实例代码)
目录 并查集 rank 的优化 Java 实例代码 UnionFind3.java 文件代码: 并查集 rank 的优化 上一小节介绍了并查集基于 size 的优化,但是某些场景下,也会存在某些问题,如下图所示,操作 union(4,2)。 根据上一小节&…...

TDA4超级玩家浮出水面,行泊一体功能、成本刷到极致
2023年以来,智能驾驶市场进入L2普及、高阶ADAS功能(NOA)大规模量产的新周期,降本增效,打造极致性价比、提升用户体验等,成为了竞争的焦点。 其中,替换更具性价比的硬件平台、传感器复用、系统优…...

3分钟了解Android中稳定性测试
一、什么是Monkey Monkey在英文里的含义是猴子,在测试行业的学名叫“猴子测试”,指的是没有测试经验的人甚至是根本不懂计算机的人(就像一只猴子),不需要知道程序的任何用户交互方面的知识,给他一个程序&a…...
LVS-DR+keepalived实现高可用负载群集
VRRP 通信原理: VRRP就是虚拟路由冗余协议,它的出现就是为了解决静态路由的单点故障。 VRRP是通过一种竞选的一种协议机制,来将路由交给某台VRRP路由。 VRRP用IP多播的方式(多播地址224.0.0.18)来实现高可用的通信&…...

阿里云国际版注册教程
什么是阿里云国际版? 阿里云国际版是阿里云专为海外客户供给的服务器及核算资源,涵盖了云主机、弹性裸金属服务器、容器服务、数据库及安全和监控等一系列云核算解决方案。 与其他云核算服务供给商不同,阿里云国际版在安全性、稳定性、性能方…...

基于百度文心大模型创作的实践与谈论
文心概念 百度文心大模型源于产业、服务于产业,是产业级知识增强大模型。百度通过大模型与国产深度学习框架融合发展,打造了自主创新的AI底座,大幅降低了AI开发和应用的门槛,满足真实场景中的应用需求,真正发挥大模型…...
)
Java基础知识题(五)
系列文章目录 Java基础知识题(一) Java基础知识题(二) Java基础知识题(三) Java基础知识题(四) Java基础知识题(五) 文章目录 系列文章目录 前言 一 Java的数据连接——JDBC 1. 简述什么是JDBC?重点 2. JDBC PreparedStatement比Statement有什么优势&…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

Qwen系列之Qwen3解读:最强开源模型的细节拆解
文章目录 1.1分钟快览2.模型架构2.1.Dense模型2.2.MoE模型 3.预训练阶段3.1.数据3.2.训练3.3.评估 4.后训练阶段S1: 长链思维冷启动S2: 推理强化学习S3: 思考模式融合S4: 通用强化学习 5.全家桶中的小模型训练评估评估数据集评估细节评估效果弱智评估和民间Arena 分析展望 如果…...
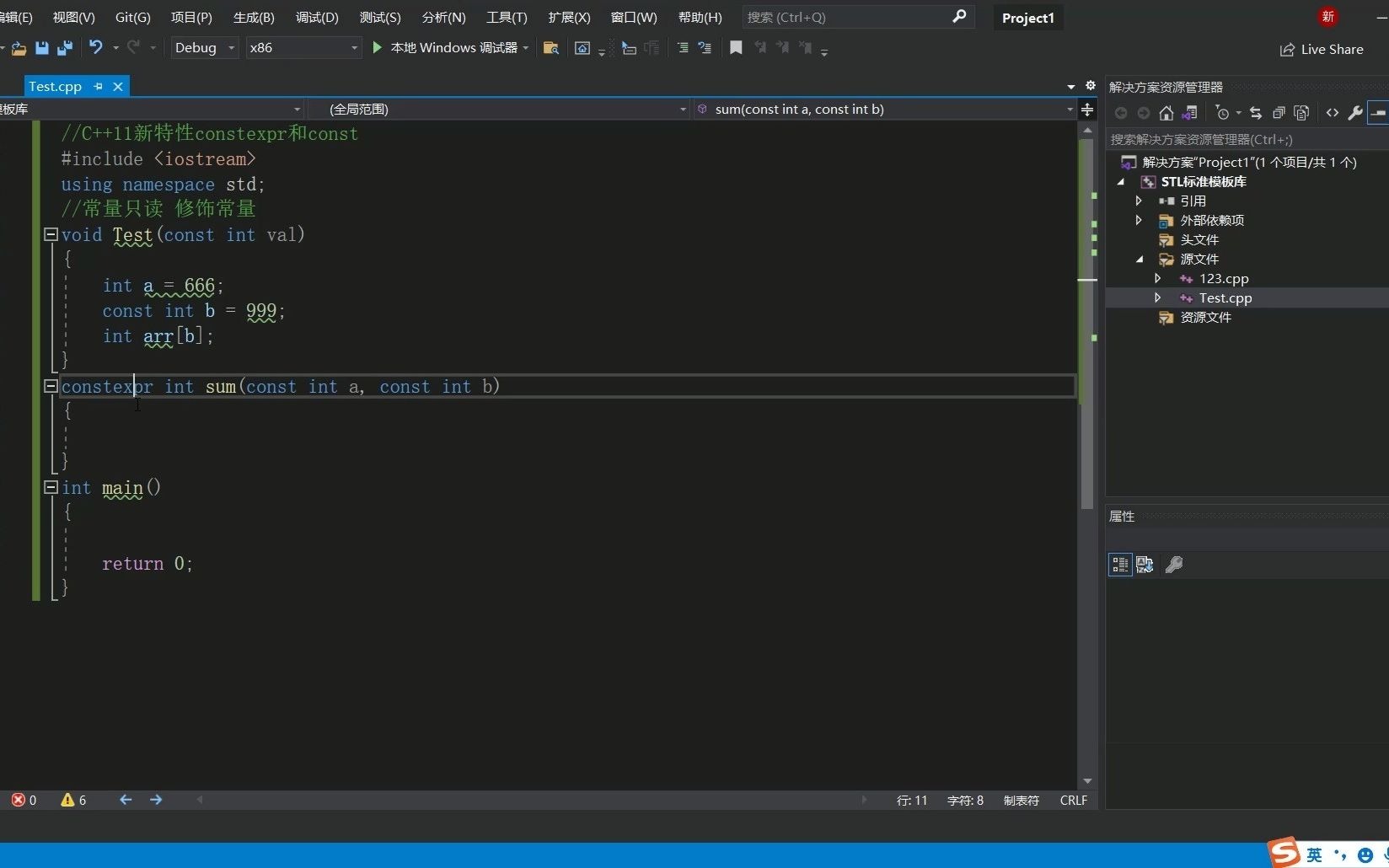
C++11 constexpr和字面类型:从入门到精通
文章目录 引言一、constexpr的基本概念与使用1.1 constexpr的定义与作用1.2 constexpr变量1.3 constexpr函数1.4 constexpr在类构造函数中的应用1.5 constexpr的优势 二、字面类型的基本概念与使用2.1 字面类型的定义与作用2.2 字面类型的应用场景2.2.1 常量定义2.2.2 模板参数…...
