迷路的机器人(递归回溯+动态规划两个方法实现)
题目:
设想有个机器人坐在一个网格的左上角,网格 r 行 c 列。机器人只能向下或向右移动,但不能走到一些被禁止的网格(有障碍物)。设计一种算法,寻找机器人从左上角移动到右下角的路径。
示例:
输入:
[
[0,0,0],
[0,1,0],
[0,0,0]
]
输出: [[0,0],[0,1],[0,2],[1,2],[2,2]]
解释:
输入中标粗的位置即为输出表示的路径,即
0行0列(左上角) -> 0行1列 -> 0行2列 -> 1行2列 -> 2行2列(右下角)
解题思路:动态规划
1.先找到可行的路径,不可达的坐标点 dp=0
2.如果终点的dp不为0,说明存在可达的路径
3.那么就从终点往回走,找到可以到达起点的路径,每走一步都要将坐标添加到res数组中
4.由于是从后往前的,所以要将res进行反转
源代码如下:
class Solution {
public:vector<vector<int>> pathWithObstacles(vector<vector<int>>& obstacleGrid) {vector<vector<int>> res;if(obstacleGrid.size()==0) return res;//矩阵为空,直接返回空数组int m=obstacleGrid.size();int n=obstacleGrid[0].size();//矩阵的起点和终点不可达,则返回空数组if(obstacleGrid[0][0]==1||obstacleGrid[m-1][n-1]==1) return res;int dp[m][n];//定义动态规划数组dp[0][0]=1;//起点位置可达,置为1//先找第一列的元素是否可达for(int i=1;i<m;i++){//不可达,dp置为0if(obstacleGrid[i][0]==1) dp[i][0]=0;//可达,则dp等于上一行的else{dp[i][0]=dp[i-1][0];}}//找第一行的元素for(int i=1;i<n;i++){if(obstacleGrid[0][i]==1) dp[0][i]=0;else{dp[0][i]=dp[0][i-1];}}//其他剩余元素for(int i=1;i<m;i++){for(int j=1;j<n;j++){if(obstacleGrid[i][j]==1) dp[i][j]=0;else{dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}}//如果终点的dp=0,说明不能到达终点,则返回空数组if(dp[m-1][n-1]==0) return res;//以下情况是已经找到路径了,只需要把路径添加到res中//从后往前找可以到达的点int i=m-1,j=n-1;while(i!=0||j!=0){res.push_back({i,j});//往上走int up=0;if(i>0) up=dp[i-1][j];//往左走int left=0;if(j>0) left=dp[i][j-1];//哪个dp值不为0,则走哪个方向if(up>=left) i--;else j--;}//最后把起点添加到数组中res.push_back({0,0});//再将数组翻转,就是正确顺序了reverse(res.begin(),res.end());return res;}
};解题思路:回溯
需要注意的是,要添加一个访问数组,标记该坐标是否已经被访问过。详解看代码
源代码如下:
class Solution {
public:bool isfind=false;//是否已经找到路径void dfs(vector<vector<int>>& obstacleGrid,vector<vector<int>>& res,vector<vector<bool>>& visited,int m,int n,int i,int j){//如果下标i和j越界//如果已经找到路径(isfind==true)//如果当前坐标有障碍物//如果当前坐标已访问//遇到以上这些情况 直接返回if(i<0||i>=m||j<0||j>=n||isfind||obstacleGrid[i][j]==1||visited[i][j]) return;//当前坐标已经到达终点,说明找到路径了if(i==m-1&&j==n-1){isfind=true;//isfind置为真res.push_back({i,j});//将终点添加到数组中//并返回return;}//其余正常情况,每遍历一个坐标,就将该坐标标记为已访问visited[i][j]=true;res.push_back({i,j});//坐标添加到数组中//递归,往下走dfs(obstacleGrid,res,visited,m,n,i+1,j);//递归,往右走dfs(obstacleGrid,res,visited,m,n,i,j+1);//回溯if(!isfind) res.pop_back();}vector<vector<int>> pathWithObstacles(vector<vector<int>>& obstacleGrid) {vector<vector<int>> res;int m=obstacleGrid.size();int n=obstacleGrid[0].size();if(obstacleGrid.size()==0) return res;//标记当前坐标是否已经访问过,初始值都为falsevector<vector<bool>> visited(m, vector<bool>(n, false));if(obstacleGrid[0][0]==1||obstacleGrid[m-1][n-1]==1) return res;dfs(obstacleGrid,res,visited,m,n,0,0);return res;}
};相关文章:
)
迷路的机器人(递归回溯+动态规划两个方法实现)
题目: 设想有个机器人坐在一个网格的左上角,网格 r 行 c 列。机器人只能向下或向右移动,但不能走到一些被禁止的网格(有障碍物)。设计一种算法,寻找机器人从左上角移动到右下角的路径。 示例:…...
Nacos
Nacos介绍 Nacos /nɑ:kəʊs/ 是 Dynamic Naming and Configuration Service的⾸字⺟简称,⼀个更易于构 建云原⽣应⽤的动态服务发现、配置管理和服务管理平台。 在这个介绍中,可以看出Nacos⾄少有三个核⼼功能: 1. 动态服务发现 2. 配…...
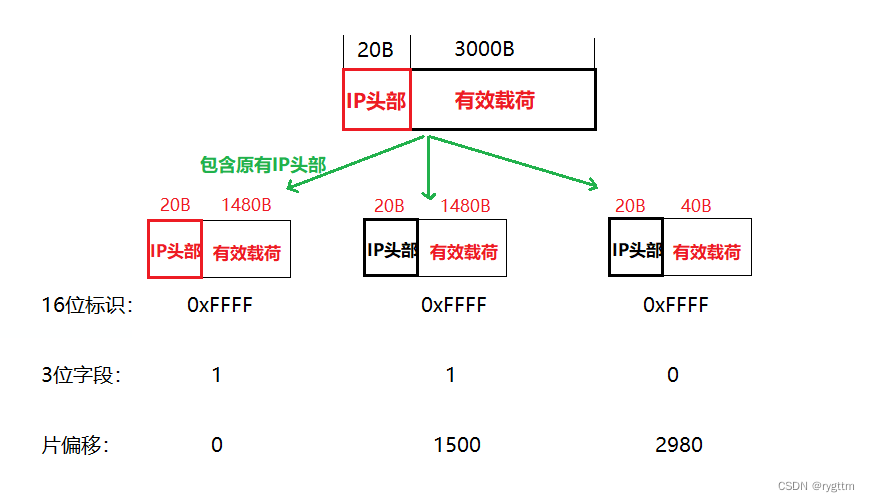
【Linux】网络层协议:IP
我们必须接受批评,因为它可以帮助我们走出自恋的幻象,不至于长久在道德和智识上自我陶醉,在自恋中走向毁灭,事实上我们远比自己想象的更伪善和幽暗。 文章目录 一、IP和TCP之间的关系(提供策略 和 提供能力)…...
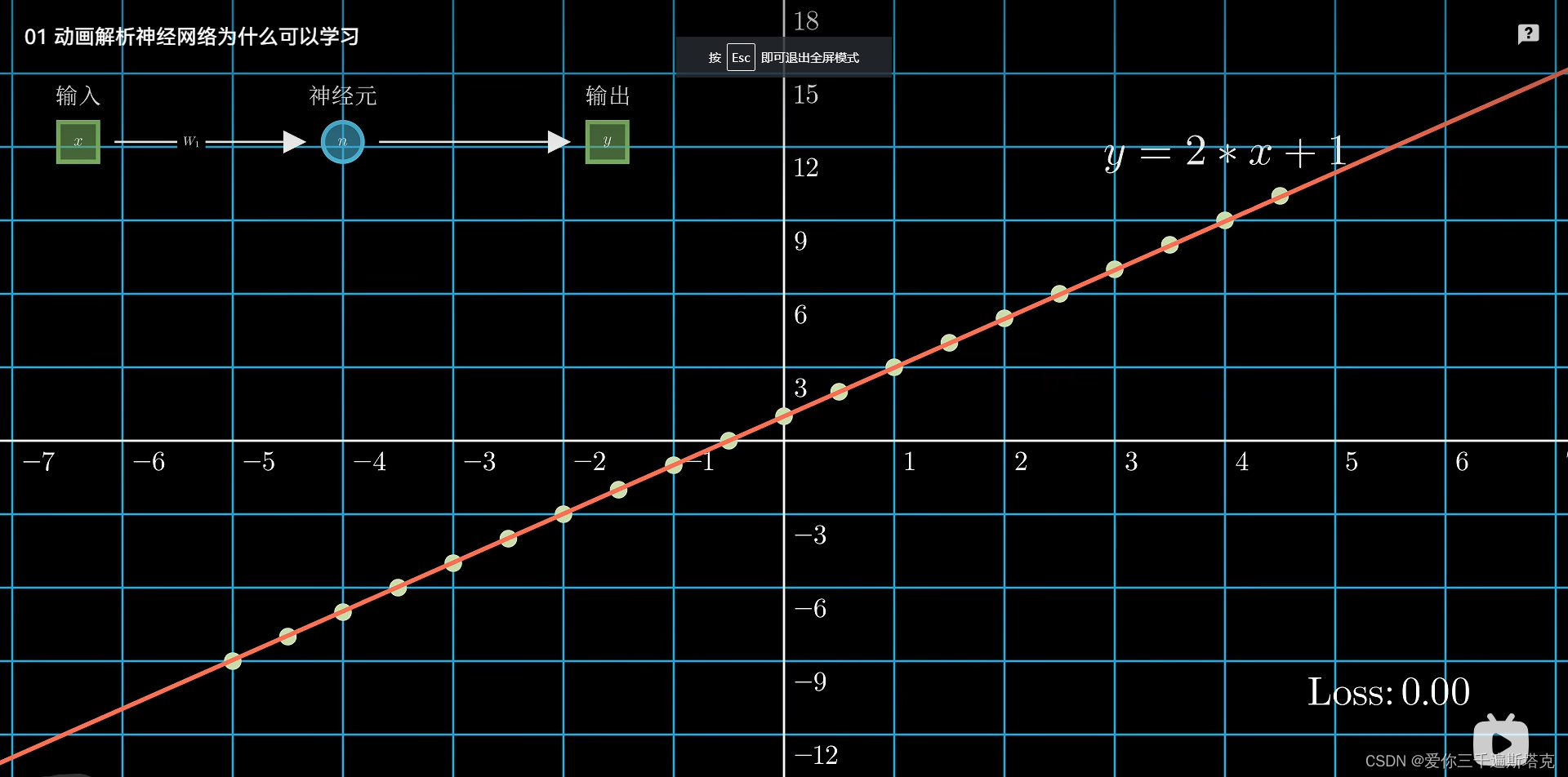
神经网络为什么可以学习
本资料转载于B站up主:大模型成长之路,仅用于学习和讨论,如有侵权请联系 动画解析神经网络为什么可以学习_哔哩哔哩_bilibilis 1、一个神经网络是由很多神经元形成的 1.1 也可以是一层,也可以是多层 2 层和层之间的连接就跟一张网一样 2.1 每…...

Docker基础入门:镜像、容器导入导出与私有仓库搭建
Docker基础入门:镜像导入导出与私有仓库搭建 一、 Docker镜像、容器的导入和导出1.1、Docker镜像的导出1.2、Docker镜像的载入1.3、Docker容器的导出1.4、Docker容器的导入 二、 镜像和容器导出和导入的区别:三、commit操作_本地镜像发布到阿里云3.1、commit操作有关…...

Go语言入门指南:基础语法和常用特性解析(上)
一、Go语言前言 Go是一种静态类型的编译语言,常常被称作是21世纪的C语言。Go语言是一个开源项目,可以免费获取编译器、库、配套工具的源代码,也是高性能服务器和应用程序的热门选择。 Go语言可以运行在类UNIX系统——比如Linux、OpenBSD、M…...
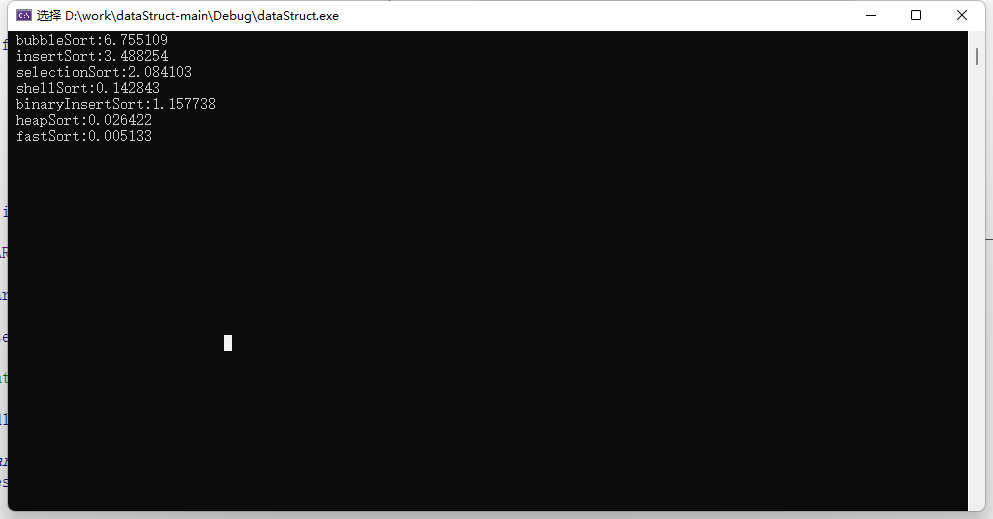
排序算法合集
F B I W a r n i n g : \color{red}FBI \qquad Warning: FBIWarning: 本人没有完整的计算机科班的教育经历,但是一直在兢兢业业,努力学习。 这些排序函数都是自己零零散散写的,也没有经过深思熟虑和优化,纯粹是为了自娱自乐。 …...
Vue2-全局事件总线、消息的订阅与发布、TodoList的编辑功能、$nextTick、动画与过渡
🥔:高度自律即自由 更多Vue知识请点击——Vue.js VUE2-Day9 全局事件总线1、安装全局事件总线2、使用事件总线(1)接收数据(2)提供数据(3)组件销毁前最好解绑 3、TodoList中的孙传父&…...

DP读书:鲲鹏处理器 架构与编程(八)3.1鲲鹏处理器片上系统与Taishan处理器内核架构
鲲鹏处理器片上系统架构 一、鲲鹏处理器片上系统与Taishan处理器内核架构1. 鲲鹏处理器片上系统概况a. 鲲鹏处理器片上系统与鲲鹏芯片家族b. 鲲鹏920处理器片上系统的组成部件c. 鲲鹏920处理器片上系统的特征d. 鲲鹏920处理器片上系统的逻辑结构 2. Taishan V110 处理器内核微架…...
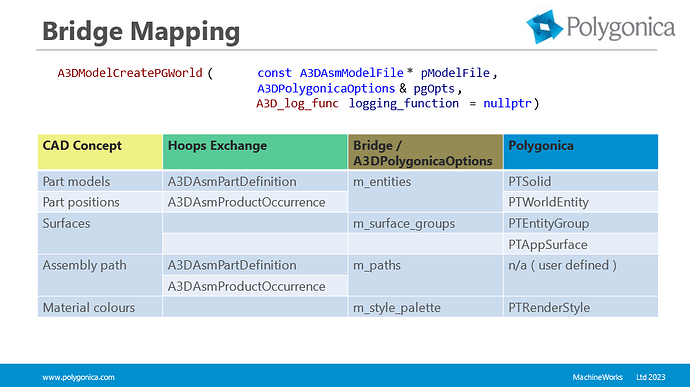
如何使用 HOOPS Exchange SDK 和 Polygonica Bridge
这里将讨论使用 HOOPS Exchange 和 Polygonica 以及它们之间的桥梁进行 CAD 访问和网格处理。--提供Crack HOOPS 全系列SDK HOOPS Exchange 基础知识 首先,让我们简单回顾一下 HOOPS Exchange。HOOPS Exchange 是一款具有 C 接口的数据访问 SDK,支持导入…...

spring异步框架使用教程
背景 在需求开发过程中,为了提升效率,很容易就会遇到需要使用多线程的场景。这个时候一般都会选择建一个线程池去专门用来进行某一类动作,这种任务到来的时候往往伴随着大量的线程被创建调用。而还有另外一种场景是整个任务的执行耗时比较长…...

【数学建模】清风数模正课3 插值算法
插值算法 在数模比赛中,很多类型的题目都需要根据已知的函数点进行数据分析和模型处理; 当此时题目所给的数据较少时,我们就无法进行准确科学的分析,所以需要更多的数据,也就是函数点; 这就需要使用数学…...

什么是eval()?eval是用来干什么的?
一、什么是eval()? eval() 是 JavaScript 中的一个全局函数,用于解析并执行传递给它的字符串作为 JavaScript 代码。 二、eval()是用来干什么的? 当调用 eval() 时,它会将传入的字符串参数视为 JavaScript 代码,并在调用位置执…...
JavaScript-console:JavaScript控制台(Console)常用方法
一、理解 console JavaScript 控制台(console)是一个开发人员在编写 JavaScript 代码时常用的工具。它是浏览器提供的一种界面,让开发人员能够追踪代码执行的状态和结果。JavaScript 控制台可以记录代码输出的信息、警告和错误,并…...

Nginx配置前后端分离
后端地址 1.本地环境 curl --request GET \--url http://localhost:8080/by-admin/captchaImage \--header Authorization: Bearer d7a035d9-b30c-4ca5-8951-8cec90607943确认后端 ip 端口 上下文 2.测试环境 部署到测试环境可能是 换成内网ip和内网服务端口(ip、端口 可能会…...
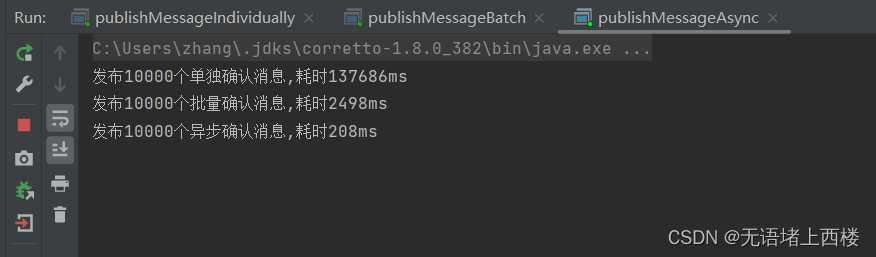
rabbitmq的发布确认
生产者将信道设置成 confirm 模式,一旦信道进入 confirm 模式, 所有在该信道上面发布的 消息都将会被指派一个唯一的 ID (从 1 开始),一旦消息被投递到所有匹配的队列之后,broker 就会发送一个确认给生产者(包含消息的唯一 ID)&…...

RISC-V公测平台发布· CoreMark测试报告
一. CoreMark简介 CoreMark是一款用于评估CPU性能的基准测试程序,它包含了多种不同的计算任务,包括浮点数、整数、缓存、内存等方面的测试。CoreMark的测试结果通常被用来作为CPU性能的参考,它可以帮助开发人员和系统管理员评估不同处理器和…...
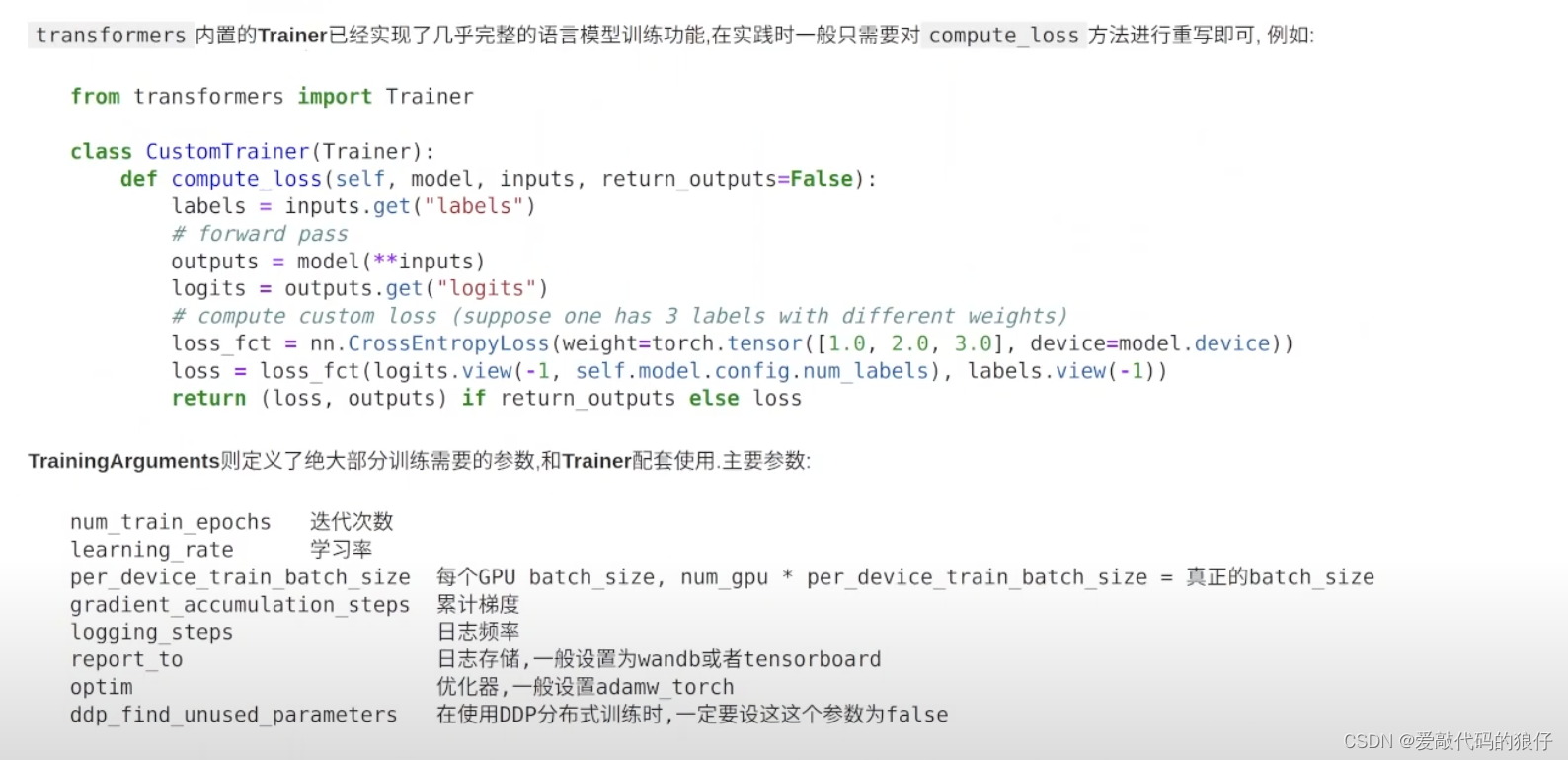
模型微调(fine-tune)
一、关于模型微调的一些基础知识 1、模型微调(fine-tune) 微调(fine-tune)通过使用在大数据上得到的预训练好的模型来初始化自己的模型权重,从而提升精度。这就要求预训练模型质量要有保证。微调通常速度更快、精度更高。当然,自己…...
云农场种植:互联网+智慧牧场,为农业注入新的活力和创新
随着科技的不断发展,数字化农业正逐渐成为现代农业的趋势。传统农业面临着土地资源有限、劳动力不足等问题,而云农场种植模式通过数字化技术的运用,互联网养殖着重于“绿色、特色产品和智慧生态”,通过建立“线上养殖线下托养线上…...

Hadoop学习一(初识大数据)
目录 一 什么是大数据? 二 大数据特征 三 分布式计算 四 Hadoop是什么? 五 Hadoop发展及版本 六 为什么要使用Hadoop 七 Hadoop vs. RDBMS 八 Hadoop生态圈 九 Hadoop架构 一 什么是大数据? 大数据是指无法在一定时间内用常规软件工具对其内…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...

Python的__call__ 方法
在 Python 中,__call__ 是一个特殊的魔术方法(magic method),它允许一个类的实例像函数一样被调用。当你在一个对象后面加上 () 并执行时(例如 obj()),Python 会自动调用该对象的 __call__ 方法…...
