【机器学习】python基础实现线性回归
手写梯度下降的实现y=kx+b的线性回归
算法步骤:
(1)构造数据,y=3*x+5;
(2)随机初始化和
,任意数值,例如
=9,
=10;
(3)计算,
,并计算
(4)分别对和
求导数,
,
其中
重复循环n次后停止
构造线性函数:

代码实现:
X=[i for i in range(0,15)]k=3
b=5
Y=[k*i+b for i in X]import matplotlib.pyplot as plt
fig, ax = plt.subplots()# 在同一个图形中绘制散点图和折线图
ax.scatter(X, Y, color='blue', label='scatter')
ax.plot(X, Y, color='red', label='line')# 添加图例
ax.legend()# 显示图形
plt.show()
MSE损失函数:
loss.append((Y[i]-y_[i])**2) #公式对应代码分别对k和b求导结果如图所示:
#公式对应代码
delta_K_sum.append((Y[i]-y_[i])*(-2)*X[i])
delta_B_sum.append((Y[i]-y_[i])*(-2))全部代码:
X=[i for i in range(0,15)]
X
k=3
b=5
Y=[k*i+b for i in X]
Y
import matplotlib.pyplot as plt
# 创建散点图
plt.scatter(X, Y)# 显示图形
plt.show()
#随机初始化要求的k和b
K=8
B=10
#k和b是正确答案,根据数据和随机初始化的K和B去拟合函数,找到最优的k和b
#y=Kx+B
loss=[]#计算预测值
for i in range(1000):y_=[K*i+B for i in X]loss=[]for i in range(len(X)):loss.append((Y[i]-y_[i])**2)print(sum(loss)/len(loss))# cha=loss.sum()/len(loss)#计算loss#根据最小二乘法 对y_求导,等我用纸写一下,利用loss对K求梯度,去更新K的值,对B求梯度,求更新B的值#直到K和B基本拟合图像delta_K_sum=[]delta_B_sum=[]for i in range(len(X)):delta_K_sum.append((Y[i]-y_[i])*(-2)*X[i])delta_B_sum.append((Y[i]-y_[i])*(-2))delta_K=sum(delta_K_sum)/len(delta_K_sum)delta_B=sum(delta_B_sum)/len(delta_B_sum)#0.01是学习率,保证稳定收敛K=K-0.01*delta_KB=B-0.01*delta_Bprint(K,B)
print(K,B)结果图像:
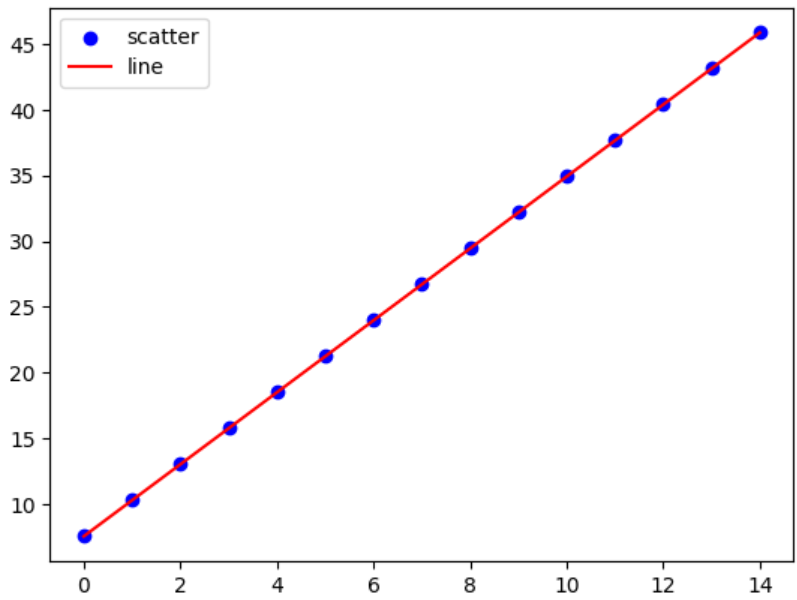
X=[i for i in range(0,15)]Y=[K*i+B for i in X]import matplotlib.pyplot as plt
fig, ax = plt.subplots()# 在同一个图形中绘制散点图和折线图
ax.scatter(X, Y, color='blue', label='scatter')
ax.plot(X, Y, color='red', label='line')# 添加图例
ax.legend()# 显示图形
plt.show()相关文章:

【机器学习】python基础实现线性回归
手写梯度下降的实现ykxb的线性回归 算法步骤: (1)构造数据,y3*x5; (2)随机初始化和,任意数值,例如9,10; (3)计算,,并计算 (4&…...
vue table合并行 动态列名
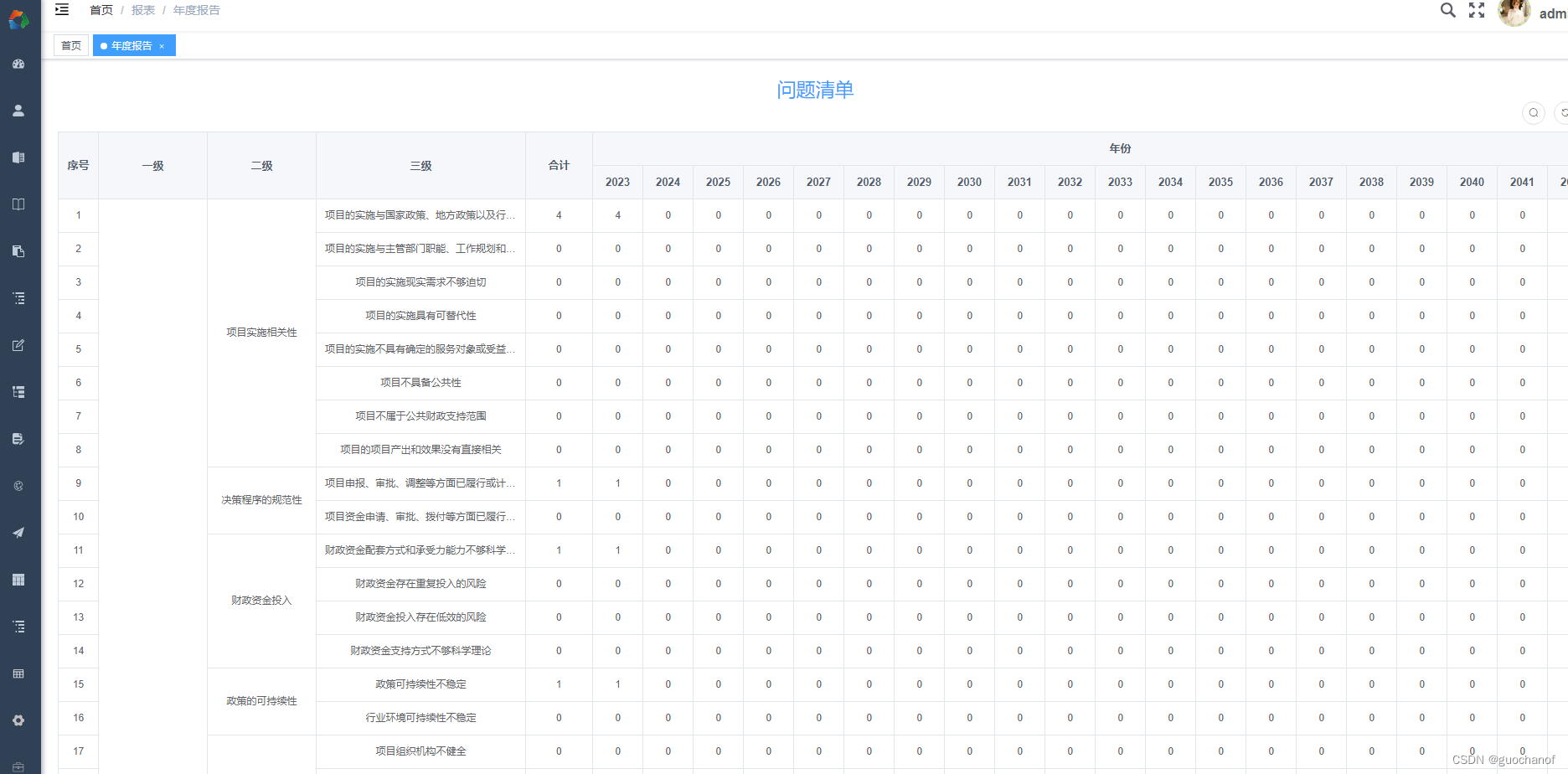
需求: 1.合并行,相同数据合并 2,根据后端返回数据动态显示列名, 我这个业务需求是,每年增加一列,也就是列名不是固定的,后端返回数据每年会多一条数据,根据返回数据显示列名 实现: html <el-table v-loading"loading" :data"dataList" :span-metho…...
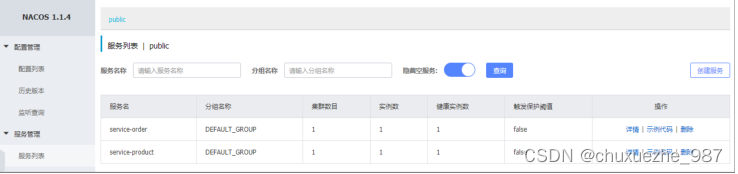
Spring Cloud Alibaba-Nacos Discovery--服务治理
1 服务治理介绍 先来思考一个问题 通过上一章的操作,我们已经可以实现微服务之间的调用。但是我们把服务提供者的网络地址 (ip,端口)等硬编码到了代码中,这种做法存在许多问题: 一旦服务提供者地址变化&am…...

【C++】unordered_map和unordered_set的使用 及 OJ练习
文章目录 前言1. unordered系列关联式容器2. map、set系列容器和unordered_map、unordered_set系列容器的区别3. unordered_map和unordered_set的使用4. set与unordered_set性能对比5. OJ练习5.1 在长度 2N 的数组中找出重复 N 次的元素思路分析AC代码 5.2 两个数组的交集思路分…...
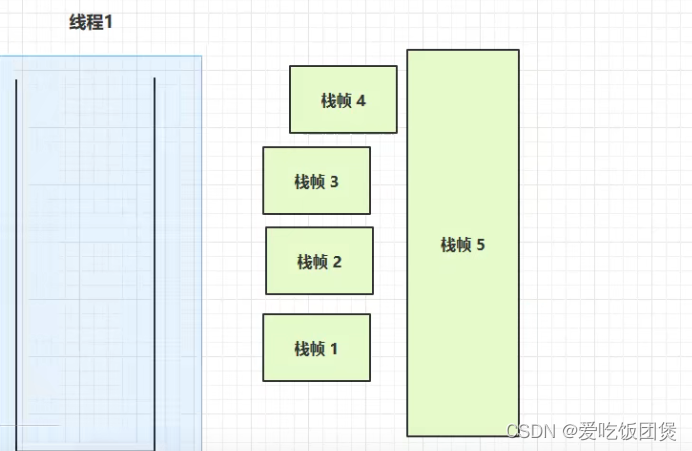
初识 JVM 01
JVM JRE JDK的关系 JVM 的内存机构 程序计数器 java指令的执行流程: 1 右侧的java源代码编译为左侧的java字节码(右侧第一个方块对应左侧第一个方块) 2 字节码 经过解释器 变为机器码 3 机器码就可以被cpu来执行 程序计数器的作用就…...

FPGA应用学习笔记----I2S和总结
时序一致在慢时序方便得多 增加了时序分布和分析的复杂性 使用fifo会开销大量资源...
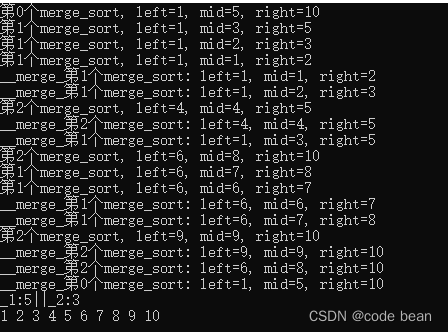
归并排序之从微观看递归
前言 这次,并不是具体讨论归并排序算法,而是利用归并排序算法,探讨一下递归。归并排序的特点在于连续使用了两次递归调用,这次我们将从微观上观察递归全过程,从本质上理解递归,如果能看完,你一…...

Pytorch-day07-模型保存与读取
PyTorch 模型保存&读取 模型存储模型单卡存储&多卡存储模型单卡读取&多卡读取 1、模型存储 PyTorch存储模型主要采用pkl,pt,pth三种格式,就使用层面来说没有区别PyTorch模型主要包含两个部分:模型结构和权重。其中模型是继承n…...

【C语言每日一题】01. Hello, World!
题目来源:http://noi.openjudge.cn/ch0101/01/ 01. Hello, World! 总时间限制: 1000ms 内存限制: 65536kB 问题描述 对于大部分编程语言来说,编写一个能够输出“Hello, World!”的程序往往是最基本、最简单的。因此,这个程序常常作为一个初…...
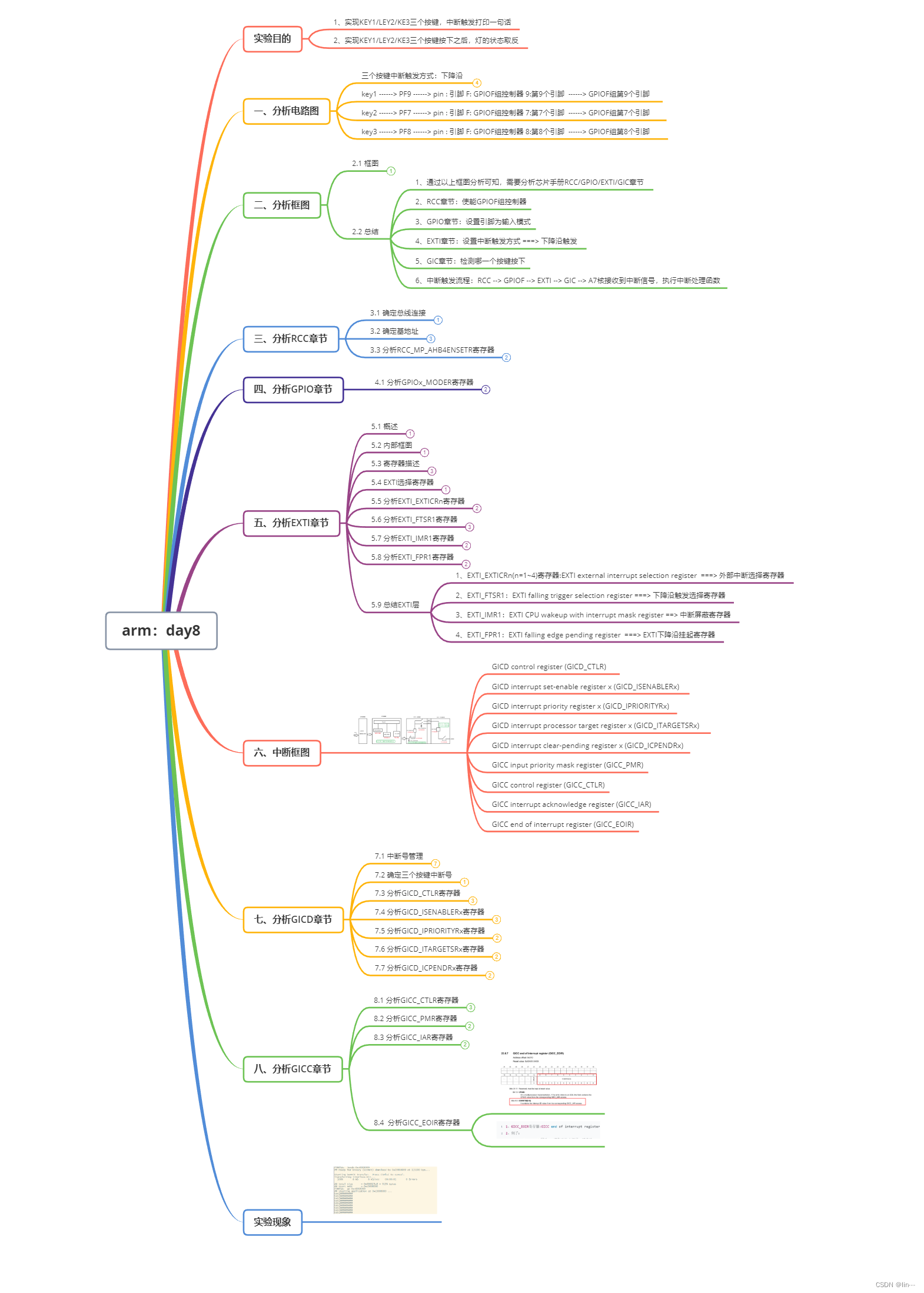
arm: day8
1.中断实验:按键控制led灯 流程: key.h /*************************************************************************> File Name: include/key.h> Created Time: 2023年08月21日 星期一 17时03分20秒***************************************…...

k8s容器加入host解析字段
一、通过edit或path来修改 kubectl edit deploy /xxxxx. x-n cattle-system xxxxx为你的资源对象名称 二、添加字段 三、code hostAliases:- hostnames:- www.rancher.localip: 10.10.2.180...

浅谈开发过程中完善的注释的重要性
第一部分:引言 1.1 简述编程注释的定义和功能 编程注释是一种在源代码中添加的辅助性文字,它不参与编译或执行,但对于理解源代码起着至关重要的作用。注释可以简单地描述代码的功能,也可以详细地解释算法的工作原理、设计决策的…...
Docker 微服务实战
1. 通过IDEA新建一个普通微服务模块 1.1 建Module docker_boot 1.2 改写pom <?xml version"1.0" encoding"UTF-8"?><project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance&…...
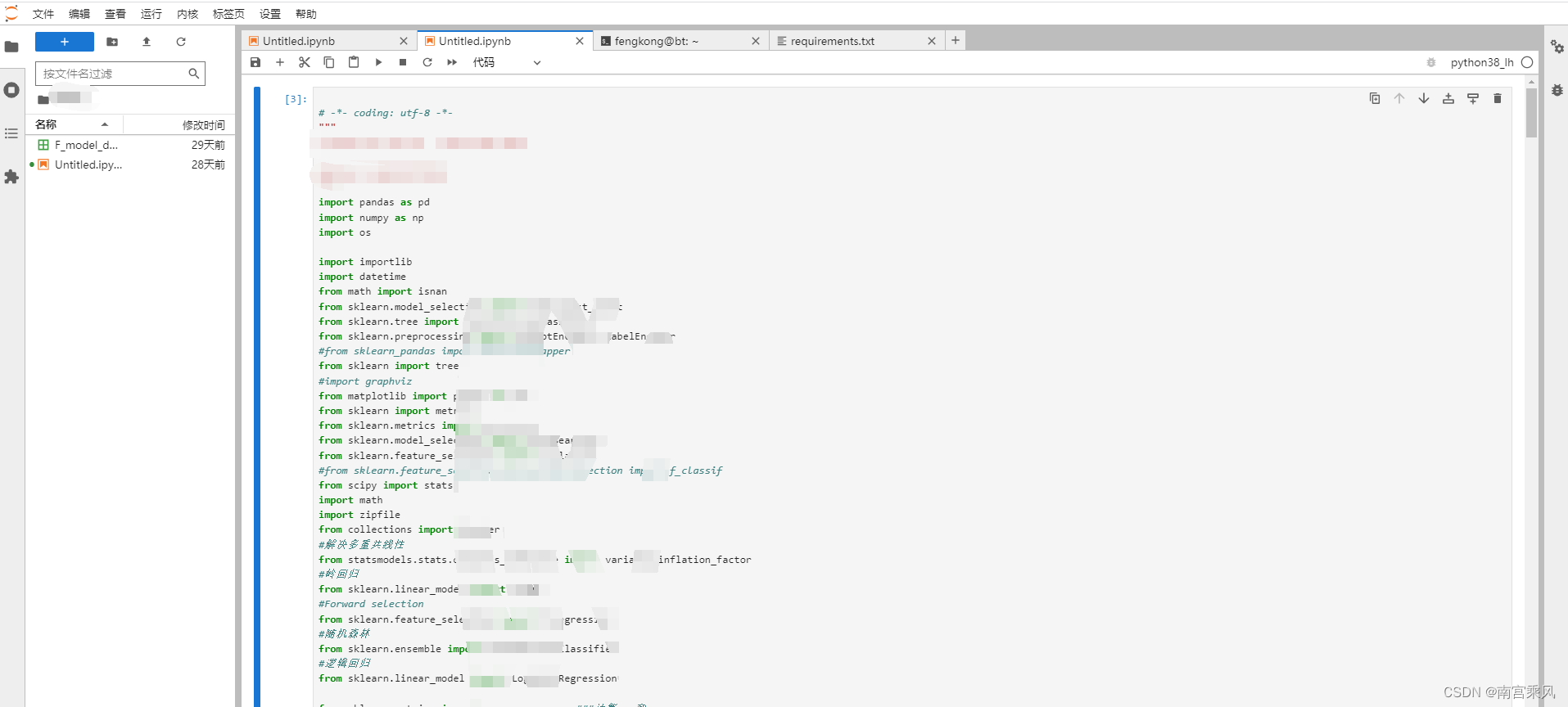
JupyterHub实战应用
一、JupyerHub jupyter notebook 是一个非常有用的工具,我们可以在浏览器中任意编辑调试我们的python代码,并且支持markdown 语法,可以说是科研利器。但是这种情况适合个人使用,也就是jupyter notebook以我们自己的主机作为服务器…...
【MySQL】视图
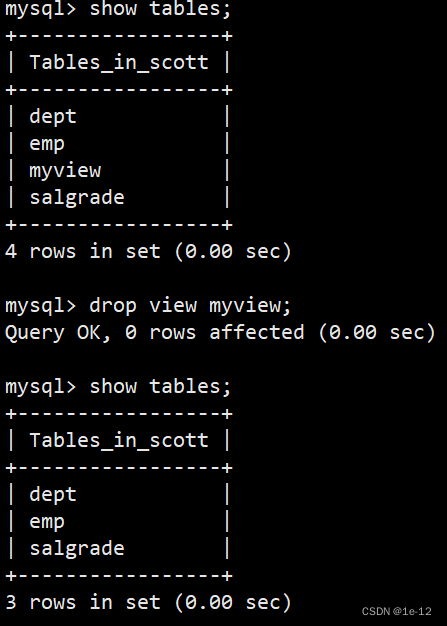
目录 一、什么是视图 二、视图的操作 2.1 创建视图 2.2 删除视图 三、视图规则和限制 一、什么是视图 视图是一个虚拟表,其内容由查询定义。同真实的表一样,视图包含一系列带有名称的列和行数据。视图的数据变化会影响到基表(创建视图所…...
基于 Android 剧院购票APP的开发与设计
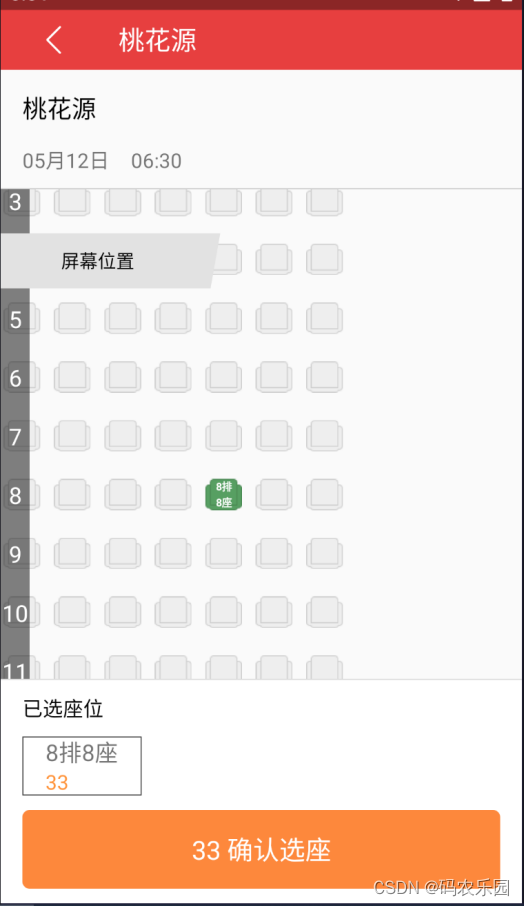
摘要:近年来,随着社会的发展和科技方面的创新,越来越多的人选择使用手机应用程序来购买剧场票。本文将探讨基于 Android 平台的剧院购票应用程序的开发和设计。该应用程序将为用户提供浏览剧场列表、查看剧场详情、选择座位并购买剧场票的功能…...

反转链表II
江湖一笑浪滔滔,红尘尽忘了 题目 示例 思路 链表这部分的题,不少都离不开单链表的反转,参考:反转一个单链表 这道题加上哨兵位的话会简单很多,如果不加的话,还需要分情况一下,像是从头节点开始…...

HTML 和 CSS 来实现毛玻璃效果(Glassmorphism)
毛玻璃效果简介 它的主要特征就是半透明的背景,以及阴影和边框。 同时还要为背景加上模糊效果,使得背景之后的元素根据自身内容产生漂亮的“变形”效果,示例: 代码实现 首先,创建一个 HTML 文件,写入如下…...
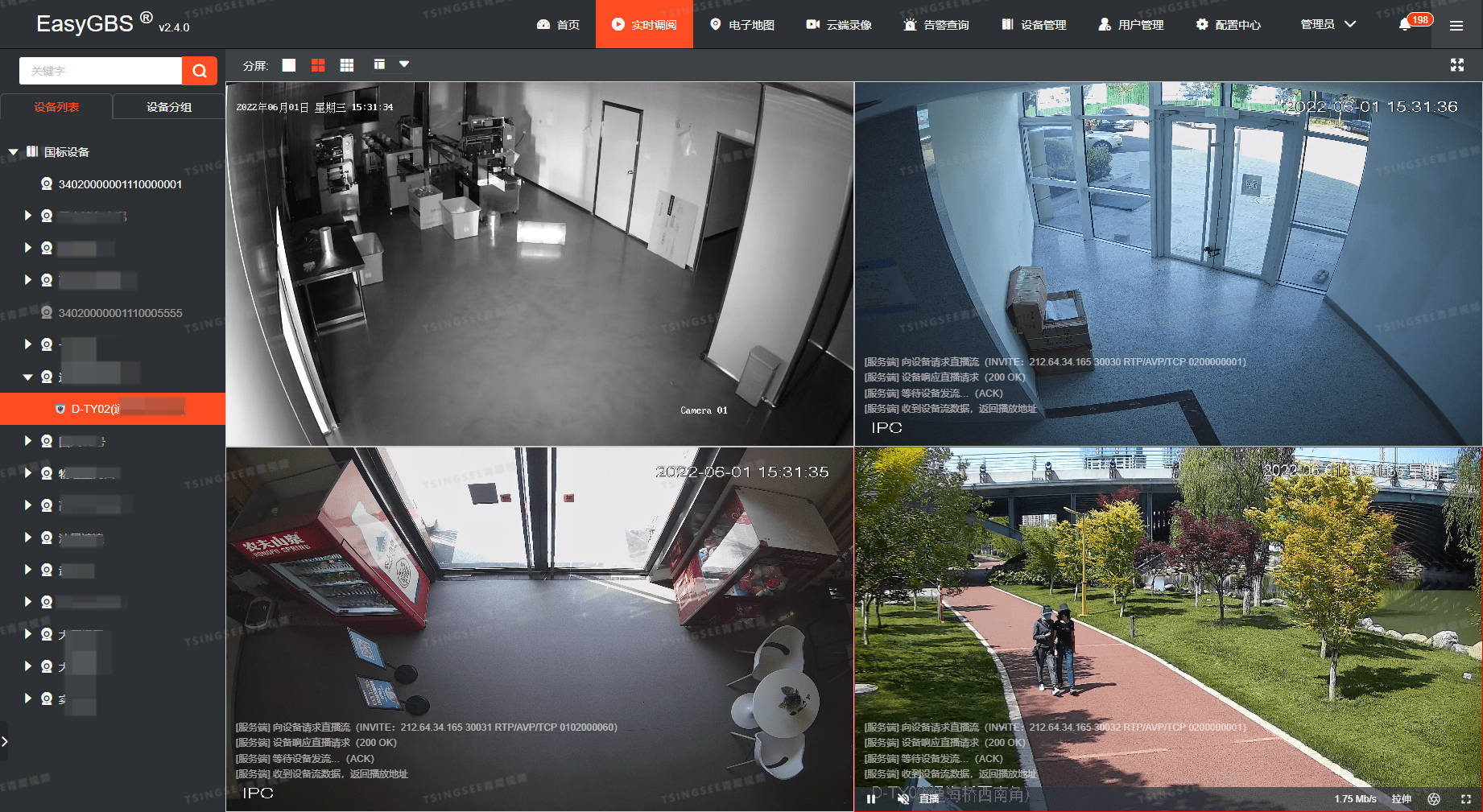
【技术】国标GB28181视频平台EasyGBS通过对应密钥上传到其他平台展示的详细步骤
国标GB28181协议视频平台EasyGBS是基于国标GB28181协议的视频云服务平台,支持多路设备同时接入,并对多平台、多终端分发出RTSP、RTMP、FLV、HLS、WebRTC等格式的视频流。平台可提供视频监控直播、云端录像、云存储、检索回放、智能告警、语音对讲、平台级…...

SpeedBI数据可视化工具:浏览器上做分析
SpeedBI数据分析云是一种在浏览器上进行数据可视化分析的工具,它能够将数据以可视化的形式呈现出来,并支持多种数据源和图表类型。 所有操作,均在浏览器上进行 在浏览器中打开SpeedBI数据分析云官网,点击【免费使用】进入&#…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
