opencv进阶19-基于opencv 决策树cv::ml::DTrees 实现demo示例
opencv 中创建决策树
cv::ml::DTrees类表示单个决策树或决策树集合,它是RTrees和
Boost的基类。
CART是二叉树,可用于分类或回归。对于分类,每个叶子节点都
标有类标签,多个叶子节点可能具有相同的标签。对于回归,每个叶
子节点都被分配了常数,因此近似函数是分段常数。
-
创建空决策树
cv::ml::DTrees::create函数可使用指定的参数创建空决策树,
之后使用cv::ml::StatModel::train函数训练该决策树模型;或者使用Algorithm::load (filename)从文件中加载决策树模型。 -
模型的基本设置
以下是构建决策树模型的必要参数,绝大部分参数有默认值
- MaxDepth:树的最大可能深度
根节点的深度为零,训练算法在深度小于MaxDepth时尝试切分节
点。如果满足其他终止标准,或者树被修剪,则实际深度可以更小。默认值为INT_MAX。
设置或获取参数MaxDepth的方法如下:

- MinSampleCount:节点中的最小样本数
如果节点中的样本数小于MinSampleCount,则不会切分该节点。
默认值为10。
设置或获取参数MinSampleCount的方法如下:

- RegressionAccuracy:回归树的终止标准
如果节点中的估计值与该节点中的样本值之间的所有绝对差值小
于该参数,则该节点不会被进一步切分。默认值为0.01f。
设置或获取参数RegressionAccuracy的方法如下:

- MaxCategories:表示特征属性为类形式时最大类的数量
算法会将分类变量的可能值聚类到K≤MaxCategories群集中,以
便找到次优切分。如果训练过程尝试进行切分的离散变量需要超过
MaxCategories值,则寻找精确的最佳子集可能需要很长时间。许多决策树引擎(包括OpenCV的实现)在这种情况下将尝试通过把所有样本聚类到MaxCategories集群中来寻找次优切分,其中,某些类别会被合并在一起。
对于具有N>MaxCategories可能值的分类变量,聚类仅应用于n>2类的分类问题。在回归和只有2类分类的情况下,不采用聚类也可以有效地找到最优切分,因此在n≤2时不使用该参数。默认值为10。
设置或获取参数MaxCategories的方法如下:

- CVFolds:使用k折叠交叉验证剪枝时的交叉验证折数
如果CVFolds>1,则算法使用k折叠交叉验证程序修剪构建的决策
树,其中,k=CVFolds,默认值为10。
设置或获取参数CVFolds的方法如下:

- Use1SERule:应用1SE规则剪枝标志位
如果标志位为true,剪枝将应用1SE规则,这将使树更紧凑,更能
抵抗训练数据噪声,但准确度稍差。默认值为true。
设置或获取参数Use1SERule的方法如下:

- TruncatePrunedTree:截断剪枝树标志位,默认值为true
如果标志位为true,则从树中物理移除已修剪的分枝,否则它们
会被保留,并且可以从原始未修剪(或修剪得不那么大)的树中获得结果。
设置或获取参数truncatePrunedTree的方法如下:

- priors:先验类概率Mat数组,默认值为空矩阵Priors=Mat()。
该参数可用于将决策树偏好调整到某个类。例如,想要检测一些
罕见的异常,即在训练集中正常比异常多很多,此时只需将每个案例都视为正常,即可实现非常好的分类性能。为了避免这种情况,可以指定先验,人为地增加异常概率(高达0.5,甚至更高),因此错误分类的异常权重变得更大,这样决策树就能做出适当地调整,以更好地检测异常样本。
还可以将此参数视为预测类别的权重,以确定为错误分类提供的
相对权重。也就是说,如果第一类别的权重是1,第二类别的权重是10,则预测第二类别的每个错误等同于在预测第一类别时犯10个错误。
设置或获取参数Priors的方法如下:

- UseSurrogates:是否构建代理切分标志位
如果为true,那么将建立代理切分。代理切分指的是,如果当前
样本缺少某些特征的值,那么该样本就无法继续沿着树向下切分,也就无法到达叶子节点,即没有预测输出。在这种情况下,可以利用当前节点下面的所有子节点中的叶子节点来预测输出的平均值,作为这个样本的预测输出,故称之为代理切分。当代理切分标志位为true时,允许使用缺少的数据。此外,如果需要计算特征(属性)的重要性,则需要将代理切分标志位设置为true。
设置或获取参数UseSurrogates的方法如下:

训练决策树
与KNN一样,决策树也是使用cv::ml::StatModel::train函数(简
称train函数)来训练模型的。
train函数:

函数参数:
- samples:训练集。
- layout:指定训练集的样本排列方式。具体如下:
• ROW_SAMPLE:每个训练样本占一行的训练集。
• COL_SAMPLE:每个训练样本占一列的训练集。 - responses与训练集样本排列顺序对应的标签向量。
树从根节点开始递归构建,所有训练数据(特征向量和响应)用
于切分根节点。在每个节点中,基于某些标准找到最佳决策规则(最佳“主要”切分)。
如前文所述,在训练中基尼系数表示的“不纯度”用于分类,均方误差之和用于回归。如有必要,找到代理切分。
它们类似于训练数据的主要切分结果。使用左子节点和右子节点之间的主要和替代切分(就像在预测过程中完成的那样)来划分所有数据。该过程以递归方式切分左右节点。当出现以下任意一种情况时,每个节点的递归过程都可能会停止。
- 构造的树分支的深度已达到指定的最大值。
- 当统计上没有进一步切分节点时,节点中的训练样本数小于指
定的阈值。 - 节点中的所有样本属于同一类,或者在回归的情况下,变化太
小。 - 与随机选择相比,最佳找到的切分没有任何明显的改善。
在构建决策树时,如有必要,可以使用交叉验证程序对其进行修剪。通常,此过程仅适用于独立决策树。如果构建的树过小,则应使用自己的方案防止过拟合。
使用决策树预测
训练好的决策树模型不仅可以根据输入样本特征向量获得响应,
还可以利用决策树计算变量的重要性。
- 预测过程
了解OpenCV中决策树模型的预测过程,有助于我们理解决策树的
原理并更好地应用它。决策树的预测过程从根节点开始,从每个非叶
子节点开始,过程向左(选择左子节点作为下一个观察节点)或向右
移动,基于某个变量的值,该变量的索引存储在被观察节点中。连续
变量与分类变量的预测过程如下。
连续变量。将变量值与存储在节点中的阈值进行比较。如果该值
小于阈值,则过程向左移动,否则向右移动。例如,如果重量小于1千克,则程序向左移动,否则向右移动。
分类变量。测试离散变量值,从变量可以采用的有限值集合中查
看它是否属于某个值的子集(也存储在节点中)。如果是,则向左移动,否则向右移动。例如,如果颜色为绿色或红色,请转到左侧,否则转到右侧。
在 每 个 节 点 中 , 都 使 用 了 ( variable_index ( 阈 值 ) ,
decision_rule(子集))这样一对实体。这样一对实体被称为一个切分(在variable_index上的切分)。一旦到达叶子节点,分配给该节点的值将用作预测输出。
有时,输入向量的某些特征缺失会导致预测过程卡在某个节点
中。为了避免这种情况,决策树使用代理切分。也就是说,除最佳的“主要”切分外,每个树节点也可以被分成具有几乎相同结果的一个或多个其他变量。
决策树模型与其他机器学习模型一样,测试可以分为一次测试一
个(多个)样本或者一次性测试整个数据集上的误差。
1)一次测试一个或多个样本
使用标准的cv::ml::StatModel::predict函数(简称predict函
数)预测所提供样本的响应。
predict函数:

函数参数:
- samples:输入样本,浮点型矩阵。
- results:可选的输出结果矩阵。
- flags : 可 选 标 志 , 取 决 于 模 型 。 参 阅
cv::ml::StatModel::Flags函数。
2)一次性测试整个数据集上的误差
使用标准的cv::ml::StatModel::calcError函数(简称calcError
函数)可以测试整个数据集上的误差。该函数使用predict函数来计算错误。对于回归模型,误差计算使用均方误差MSE;对于分类模型,计算错误分类样本的百分比(0%~100%)。
calcError函数:

函数参数:
- data:可以是TrainData类型的训练数据或者测试数据。
- test:如果为true,则在数据的测试子集上计算误差,否则在
数据的训练子集上计算误差。注意,如果加载了一个完全不同的数据集 来 评 估 已 经 训 练 过 的 模 型 , 则 不 需 要 使 用
TrainData::setTrainTestSplitRatio方法设置切分测试子集,此时无论test=true还是test=false,都将计算整个新数据集的误差。 - resp:可选的输出响应。
- 计算变量的重要性
决策树不仅可用于预测,还可用于各种数据分析。前文曾介绍
过,选择最佳切分属性是决策树的关键。因此决策树具有计算每个样本属性(特征)的重要性的能力,在OpenCV中称之为计算变量重要性。例如,当使用邮件信息中出现的一组单词作为特征向量的垃圾邮件过滤器时,变量重要性评级可用于确定最“垃圾邮件指示”单词,从而有助于保持字典大小合理。
应用示例
import cv2
import numpy as np# 创建一个决策树分类器
decision_tree = cv2.ml.DTrees_create()# 创建一些训练数据
train_data = np.array([[1.0, 2.0], [2.0, 3.0], [3.0, 4.0], [10.0, 12.0], [11.0, 13.0]], dtype=np.float32)
responses = np.array([0, 0, 0, 1, 1], dtype=np.int32)# 进行PCA降维
num_components = 1
pca = cv2.PCACompute(train_data, mean=None, maxComponents=num_components)# 使用PCA进行降维
train_data_reduced = cv2.PCAProject(train_data, pca[0])# 创建一个决策树分类器
decision_tree = cv2.ml.DTrees_create()# 设置决策树参数
params = dict(maxDepth=2)
decision_tree.setCVFolds(1) # 设置交叉验证折数# 将降维后的训练数据与类别标签整合为训练集
train_data_with_labels = cv2.ml.TrainData_create(samples=train_data_reduced,layout=cv2.ml.ROW_SAMPLE,responses=responses)# 训练决策树分类器
decision_tree.train(train_data_with_labels)# 创建一个测试样本并进行降维
test_sample = np.array([[2.5, 3.5]], dtype=np.float32)
test_sample_reduced = cv2.PCAProject(test_sample, pca[0])# 使用决策树进行预测
result = decision_tree.predict(test_sample_reduced)
print("Predicted class:", result[1][0][0])
相关文章:

opencv进阶19-基于opencv 决策树cv::ml::DTrees 实现demo示例
opencv 中创建决策树 cv::ml::DTrees类表示单个决策树或决策树集合,它是RTrees和 Boost的基类。 CART是二叉树,可用于分类或回归。对于分类,每个叶子节点都 标有类标签,多个叶子节点可能具有相同的标签。对于回归,每…...

Unity通过TCP/IP协议进行通信
uinty项目中需要与C编写的硬件进行通信,因此采用TCP/IP协议进行通信,主要实现了与服务器的连接、通信内容的发送以及断开连接等功能。 根据确定好的协议格式,编写需要发送的内容,将其转为字节流(byte[])通过…...

基于VuePress搭建知识库
我这边需要搭建一个运维知识库,将项目的方方面面记录下来,方便新手接手运维。 准备环境 Nginx 1.19.0VuePress 1.xMinio RELEASE.2022-02-16T00-35-27Zvuepress-theme-vdoing主题 安装VuePress 根据官网步骤即可 # 创建目录 mkdir vuepress-starter…...

odoo安装启动遇到的问题
问题:在第一次加载odoo配置文件的时候,启动失败 方法: 1、先检查odoo.conf的内容,尤其是路径 [options] ; This is the password that allows database operations: ; admin_passwd admin db_host 127.0.0.1 db_port 5432 d…...
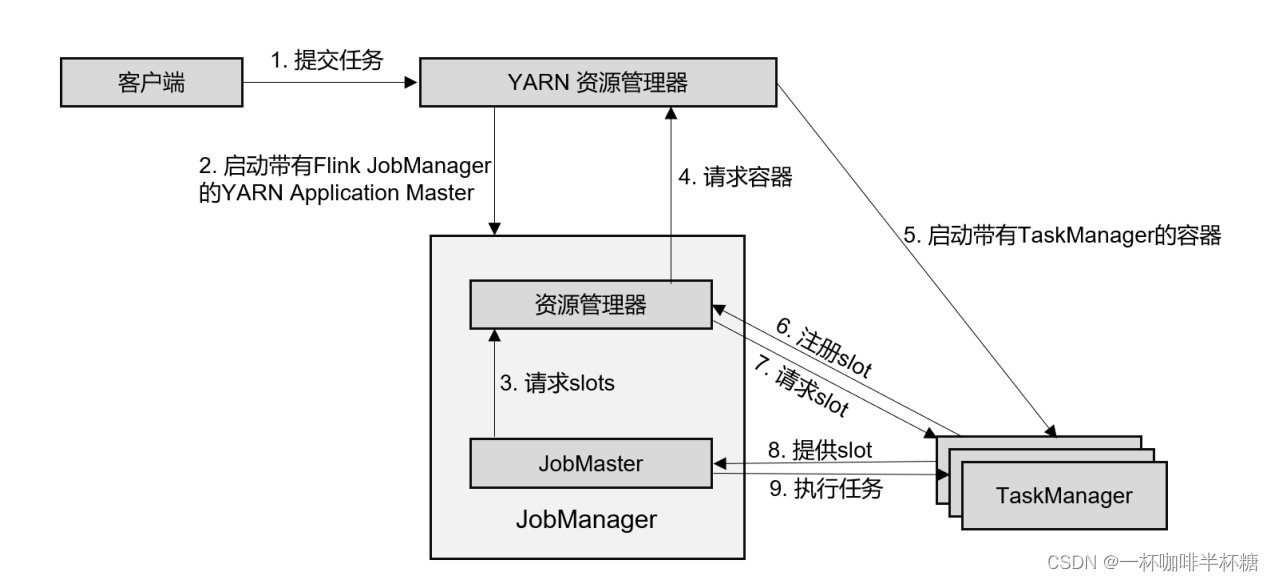
【Flink】Flink提交流程
我们通常在学习的时候需要掌握大数据组件的原理以便更好的掌握这个大数据组件,Flink实际生产开发过程中最常见的就是提交到yarn上进行调度,模式使用的Per-Job模式,下面我们就给大家讲下Flink提交Per-Job任务到yarn上的流程,流程图…...

哪种英特尔实感设备适合您?
原文链接 https://www.intelrealsense.com/which-device-is-right-for-you/ 无论您是深度和跟踪硬件的新手,还是经验丰富的专业人士,确定我们提供的众多英特尔实感产品中哪些产品适合您的项目仍然是一项挑战。在这篇文章中,我们将讨论英特尔…...

C++11的四种强制类型转换
目录 语法格式 static_cast(静态转换) dynamic_cast(动态转换) const_cast(常量转换) reinterpret_cast(重解释) 语法格式 cast-name <typename> (expression) 其中cast-name为static_cast、dynamic_cast、const_cast 和 reinterpret_cast之一…...
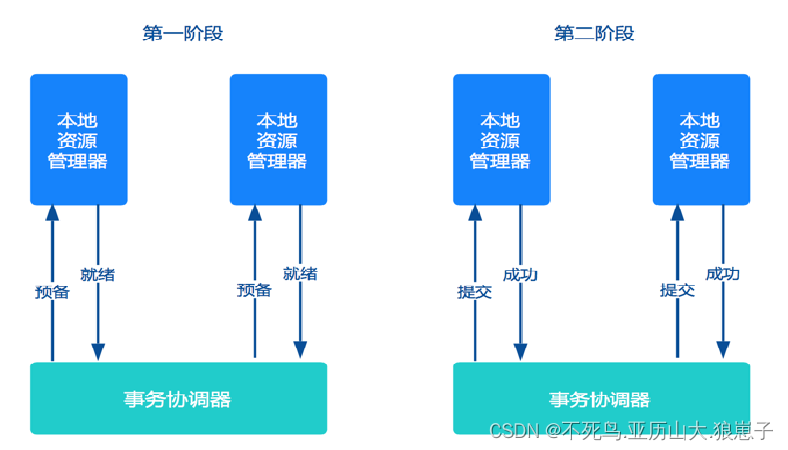
分布式事务(4):两阶段提交协议与三阶段提交区别
1 两阶段提交协议 两阶段提交方案应用非常广泛,几乎所有商业OLTP数据库都支持XA协议。但是两阶段提交方案锁定资源时间长,对性能影响很大,基本不适合解决微服务事务问题。 缺点: 如果协调者宕机,参与者没有协调者指…...
------ 实现多节点渲染【修改beginWork和completeWork】)
React源码解析18(9)------ 实现多节点渲染【修改beginWork和completeWork】
摘要 目前,我们已经实现了单节点的,beginWork,completeWork,diff流程。但是对于多节点的情况,比如: <div><span></span><span></span> </div>这种情况,我们还没有处…...

【GUI】基于开关李雅普诺夫函数的非线性系统稳定(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
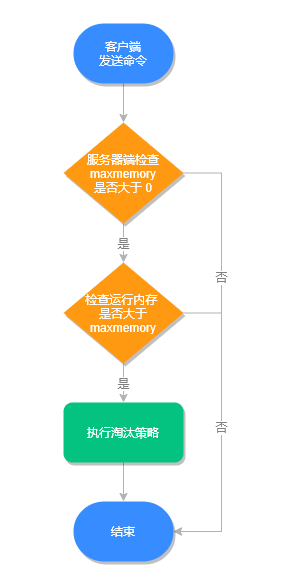
Redis 缓存满了怎么办?
引言 Redis 缓存使用内存来保存数据,随着需要缓存的数据量越来越大,有限的缓存空间不可避免地会被写满。此时,应该怎么办?本篇文章接下来就来聊聊缓存满了之后的数据淘汰机制。 值得注意的是,在 Redis 中 过期策略 和…...
Grafana 安装配置教程
Grafana 安装配置教程 一、介绍二、Grafana 安装及配置2.1 下载2.2 安装2.2.1 windows安装 - 图形界面2.2.2 linux安装 - 安装脚本 三、Grafana的基本配置3.1 登录3.2 Grafana设置中文 四、grafana基本使用 一、介绍 Grafana是一个通用的可视化工具。对于Grafana而言࿰…...

【Linux】临界资源和临界区
目录 一、临界资源 二、如何实现对临界资源的互斥访问 1、互斥量 2、信号量 3、临界区 三、临界区 四、进程进入临界区的调度原则 一、临界资源 概念:临界资源是一次仅允许一个进程使用的共享资源,如全局变量等。 二、如何实现对临界资源的互斥访问 …...

拓扑排序Topological sorting/DFS C++应用例题P1113 杂务
拓扑排序 拓扑排序可以对DFS的基础上做变更从而达到想要的排序效果。因此,我们需要xy准备,vis数组记录访问状态,每一个任务都可以在dfs的过程中完成。 在使用拓扑排序方法时一些规定: 通常使用一个零时栈不会直接输出排序的节点…...
基于jenkins构建生成CICD环境
目录 一、安装配置jenkins 1、环境配置 2、软件要求 3、jdk安装(我是最小化安装,UI自带java要先删除rm -rf /usr/local/java 4、安装jenkins-2.419-1.1 二、Jenkins配置 1、修改jenkins初始密码 2、安装 Jenkins 必要插件 3、安装 Publish Over SS…...
在线图片怎么转换成PDF?在线图片转换成PDF步骤介绍
文件格式要转化不知道怎么办?想要网上下载文件格式转换软件,但是却不知道下载哪个好?今天小编小编就给大家分享一下靠谱的小圆象PDF转换器工具,想知道这款软件好不好用?在线图片怎么转换成PDF?那就进来看看吧。 在线图片怎么转换成PDF 小圆象PDF转换…...
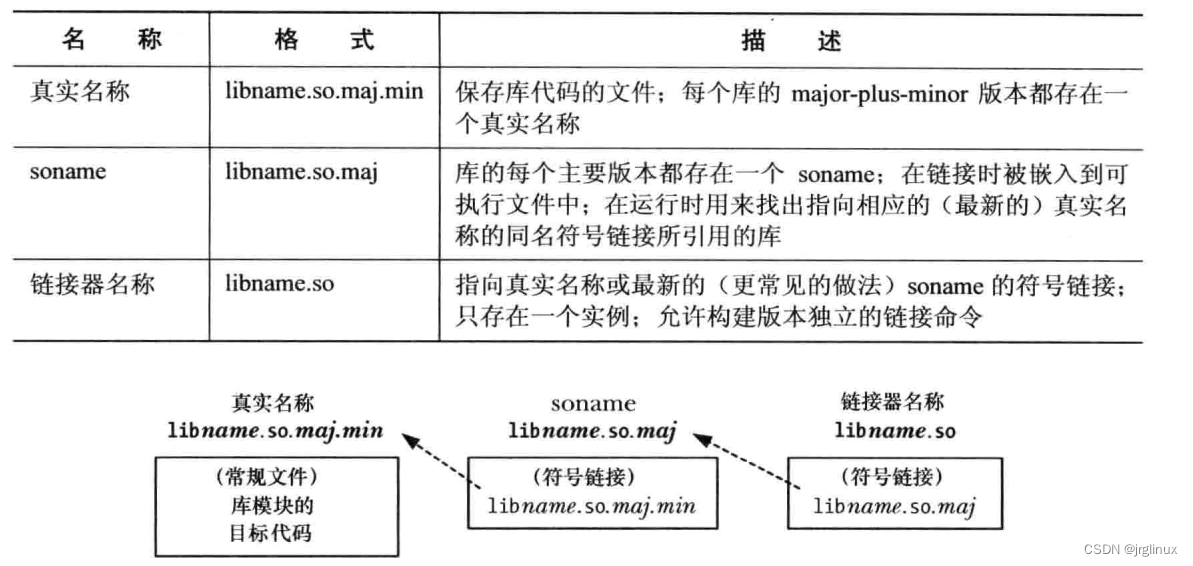
Linux共享库基础及实例
共享库是将库函数打包成一个可执行文件,使得其在运行时可以被多个进程共享。 目标库 回顾下构建程序的一种方式: 将每个源文件编译成目标文件,再通过链接器将这些目标文件链接组成一个可执行程序。 gcc -g -c prog.c mod1.c mod2.c gcc -g …...

java八股文面试[java基础]——final 关键字作用
为什么局部内部类和匿名内部类只能访问final变量: 知识来源 【基础】final_哔哩哔哩_bilibili...
Redis 分布式锁存在什么问题 ?如何解决 ?
目录 1. 如何实现分布式锁 2. Redis 分布式锁存在什么问题 2.1 解决死锁问题 2.2 解决锁误删问题 1. 如何实现分布式锁 Redis 天生就可以作为一个分布式系统来使用,所以它实现的锁都是分布式锁。 Redis 可以通过 setnx(set if not exists)…...

n5173b是德科技keysight N5173B信号发生器
产品概述 是德科技/安捷伦N5173B EXG模拟信号发生器 当您需要平衡预算和性能时,是德科技N5173B EXG微波模拟信号发生器是经济高效的选择。它提供解决宽带滤波器、放大器、接收机等参数测试的基本信号。执行基本LO上变频或CW阻塞,低成本覆盖13、20、31.…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...
