数据结构:二叉树及相关操作
文章目录
- 前言
- 一、树的概念及结构
- 1.什么是树
- 2. 树的相关概念
- 3.树的表示
- 二、二叉树概念及结构
- 1.二叉树概念
- 2.特殊的二叉树
- 3.二叉树的性质
- 4.二叉树的存储结构
- 三、平衡二叉树实现
- 1.创建树和树的前中后遍历
- 1.前中后遍历
- 2.创建树且打印前中后遍历
- 2.转换为平衡二叉树和相关操作
- 1.转换为平衡二叉树
- 2.二叉树的层序遍历
- 3.判断是否为完全二叉树
- 4.平衡二叉树的节点删除
- 3.二叉树其他操作
- 总结
前言
在实现二叉树前,我们要先对树产生一些基本的认识,才可以去实现它。树的用途非常广泛,向文件系统的目录树结构等。
一、树的概念及结构
1.什么是树
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。有一个特殊的结点,称为根结点,根节点没有前驱结点。除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继。因此,树是递归定义的。
如图所示:
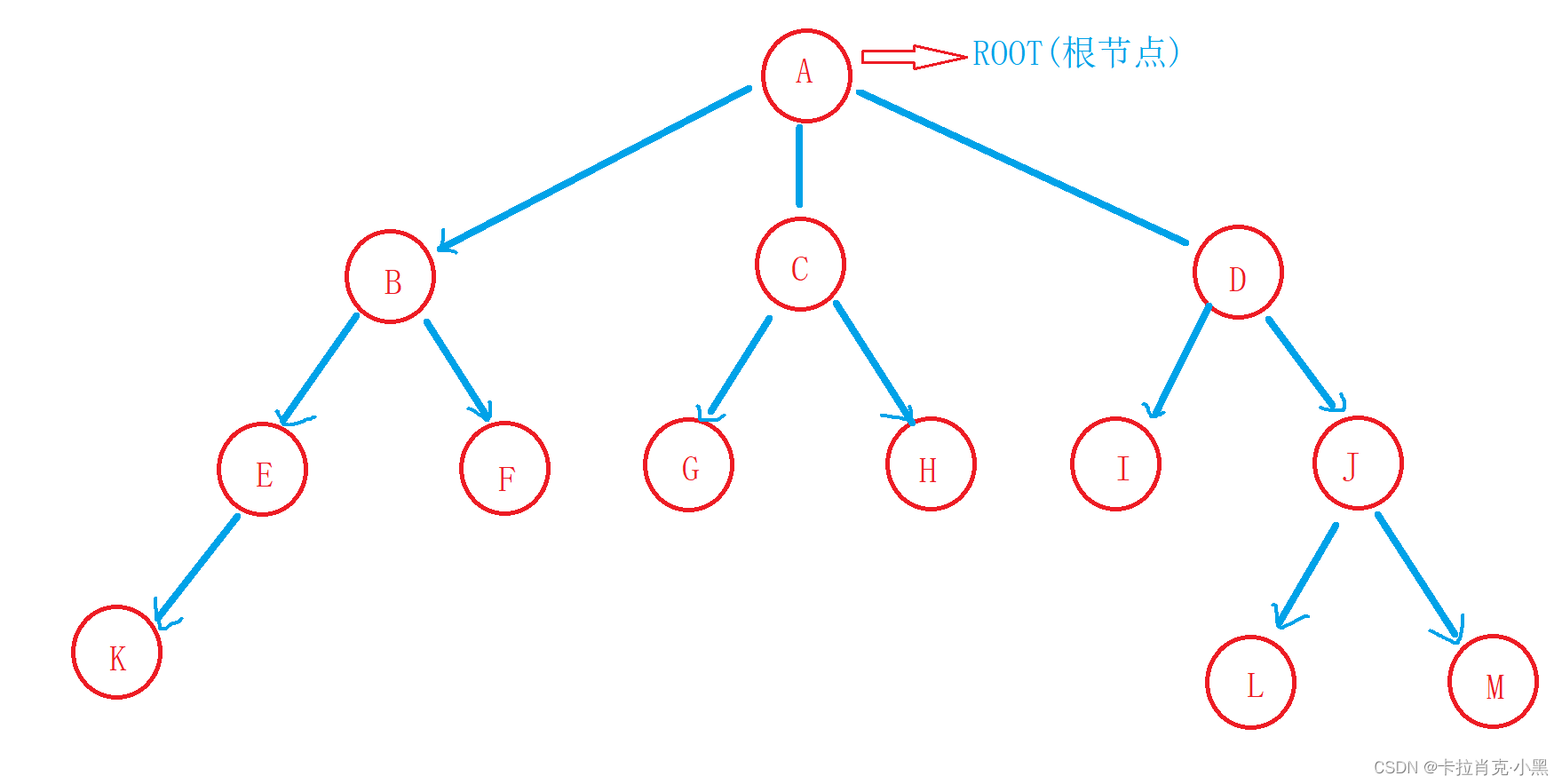
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
如图所示:
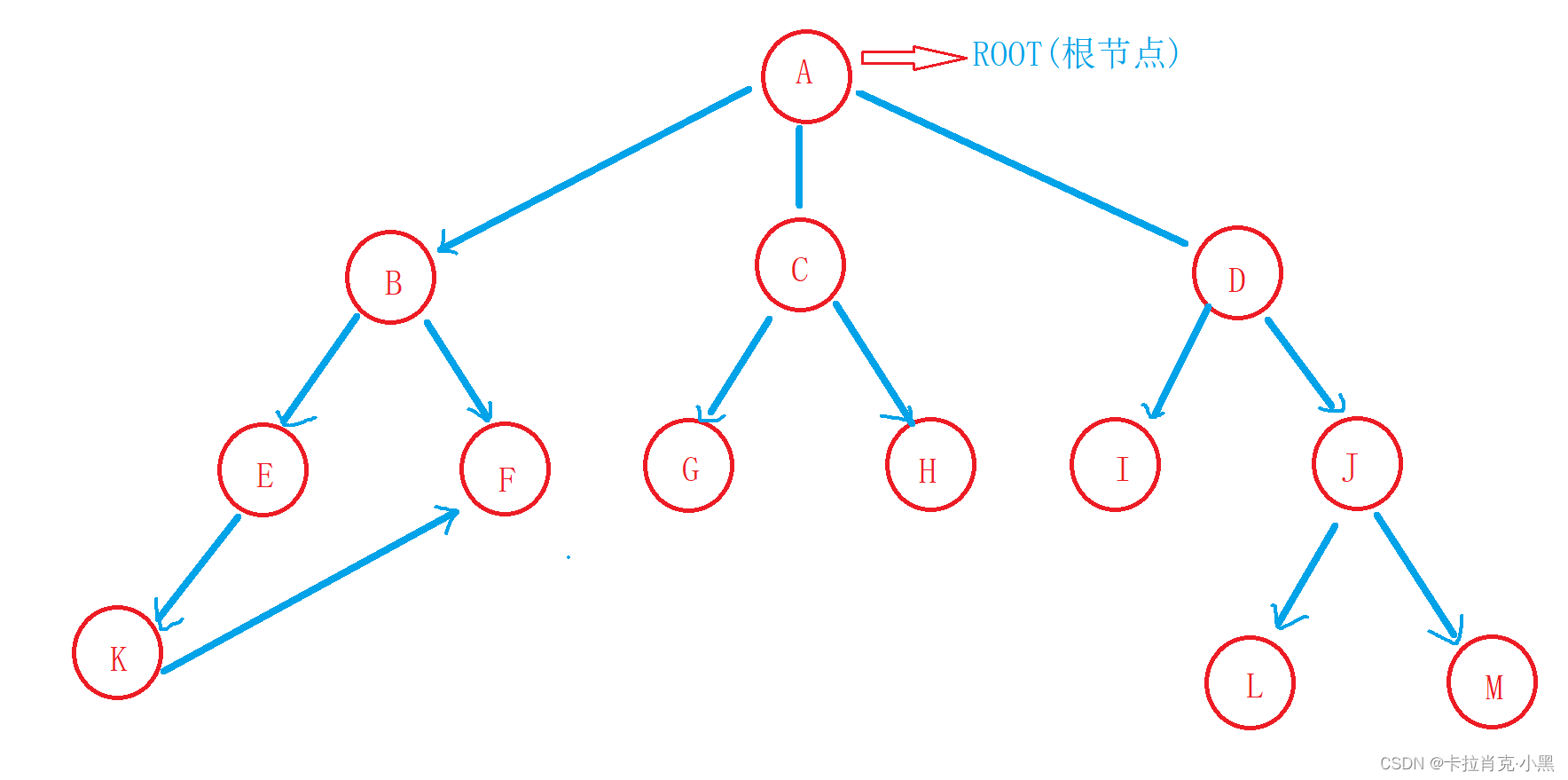
这个就不可以在称为树,这个构成了环形结构,这个是一个图。
2. 树的相关概念
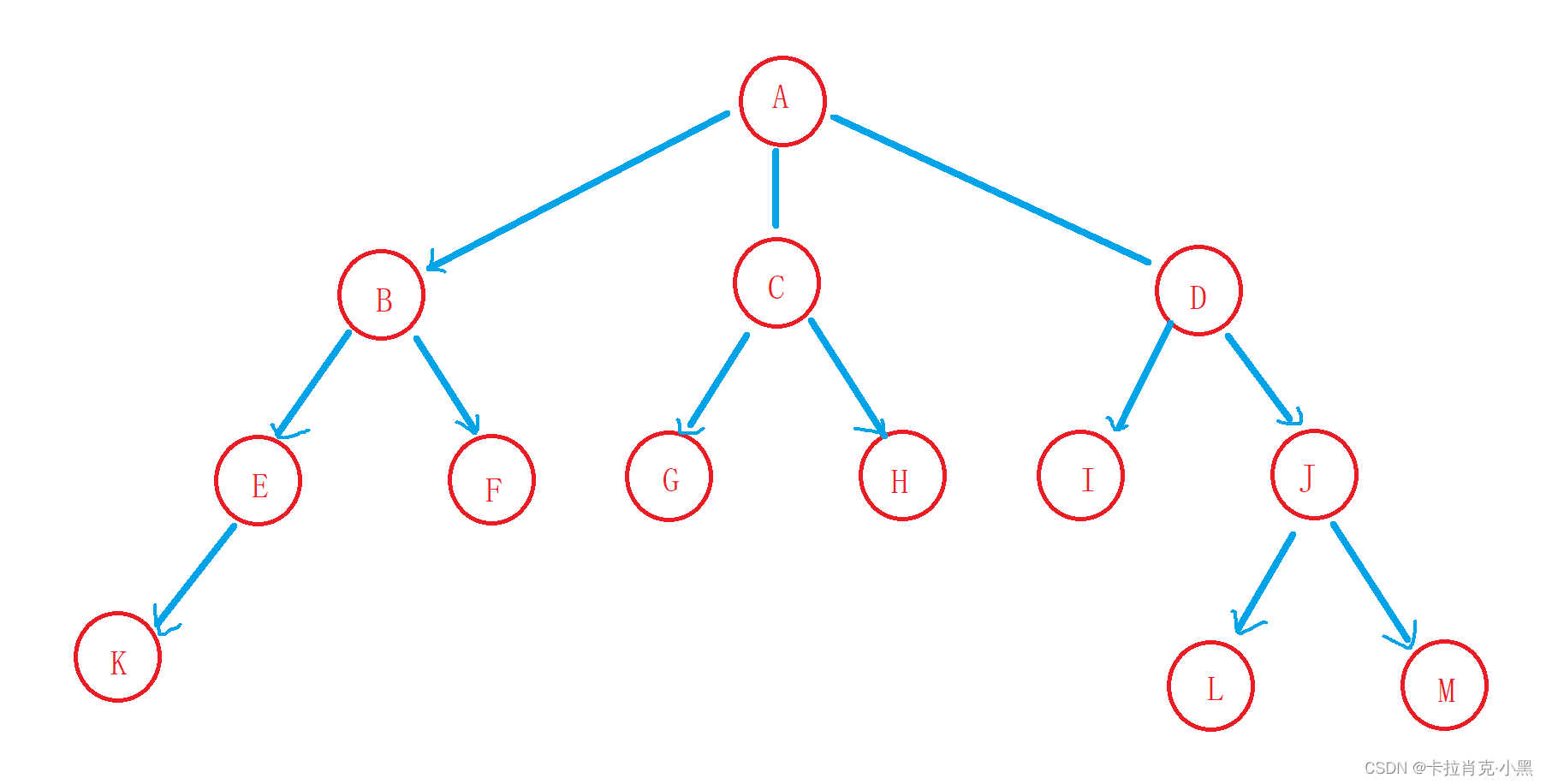
节点的度:一个节点含有的子树的个数称为该节点的度。如上图:A的度为3
树的深度:树中节点的最大层次。如上图:树的深度为4
叶子节点:度为0的节点称为叶节点。如上图:K为叶子节点
孩子节点:一个节点含有的子树的根节点称为该节点的子节点。如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点。 如上图:B、C是兄弟节点
堂兄弟节点:双亲在同一层的节点互为堂兄弟。如上图:F、G是堂兄弟节点
3.树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
typedef int DataType;
struct Node
{struct Node* firstChild1; // 第一个孩子结点struct Node* pNextBrother; // 指向其下一个兄弟结点DataType data; // 结点中的数据域
};
上面树的表示形式如下:
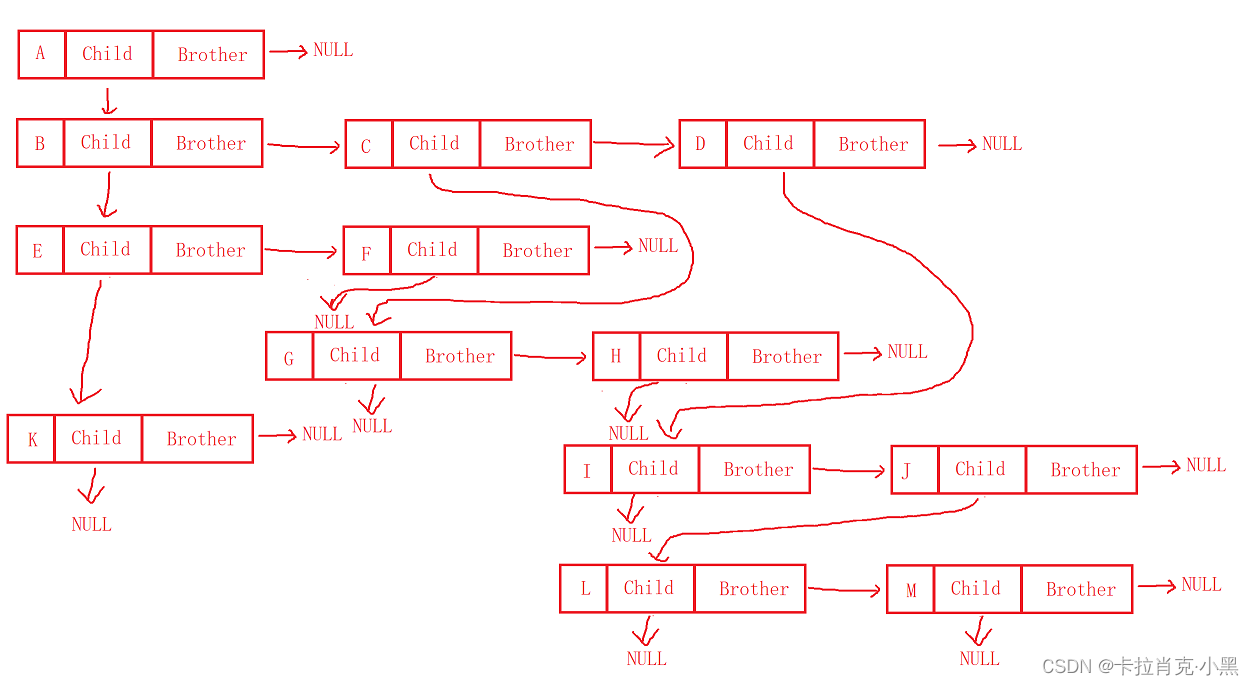
二、二叉树概念及结构
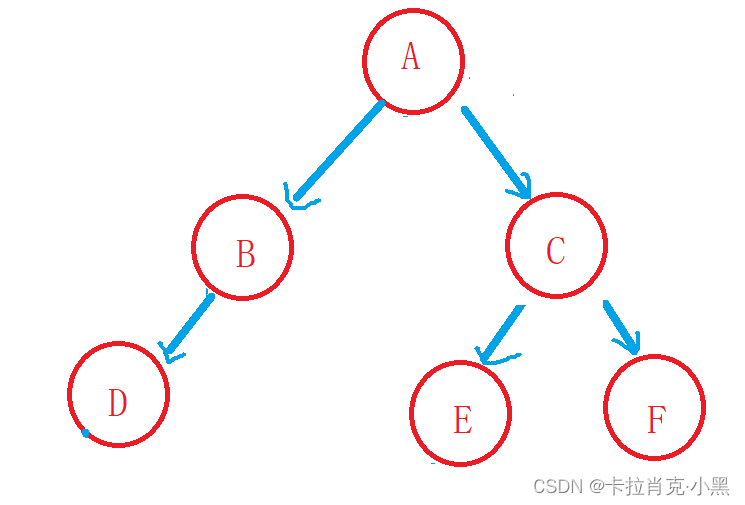
1.二叉树概念
二叉树不存在度大于2的结点
如图所示:
2.特殊的二叉树
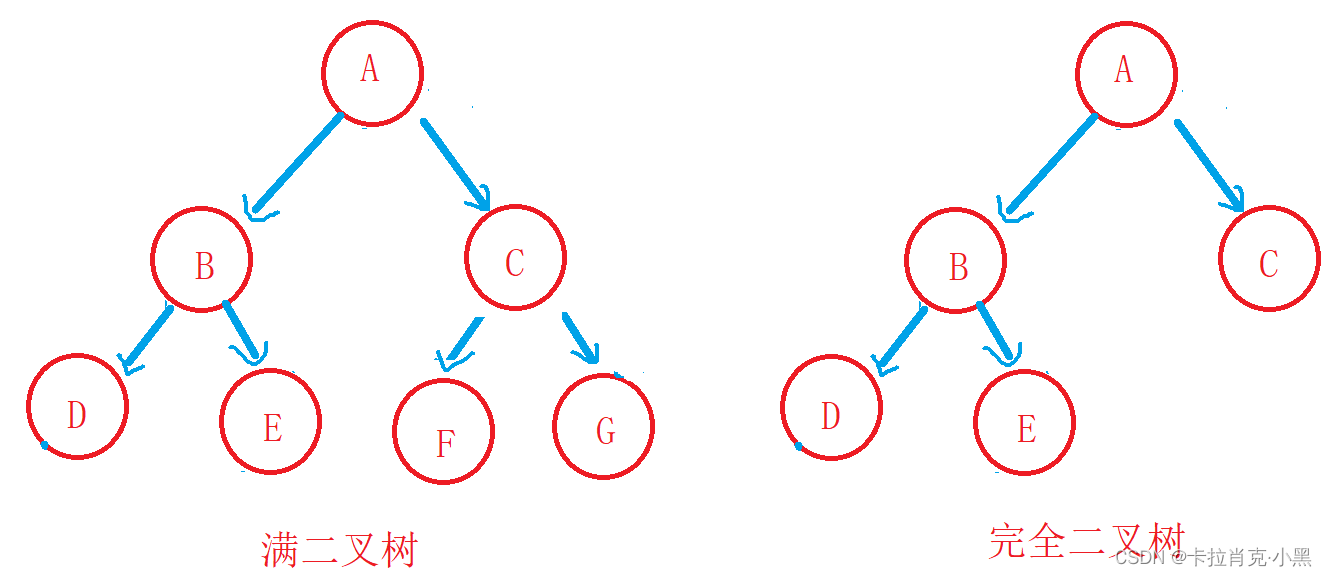
满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。
完全二叉树:对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
3.二叉树的性质
1. 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2的(i-1)次方个结点。
2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2的h次方减1个。
3. 对任何一棵二叉树,如果度为0其叶结点个数为X个 , 度为2的分支结点个数为Y个,则有X=Y+1
4.对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对
于序号为i的结点有:
1.若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
2. 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
3. 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
4.二叉树的存储结构
1. 顺序存储顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
2. 链式存储二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。

如上图所示:上面二叉树的储存形式如下:
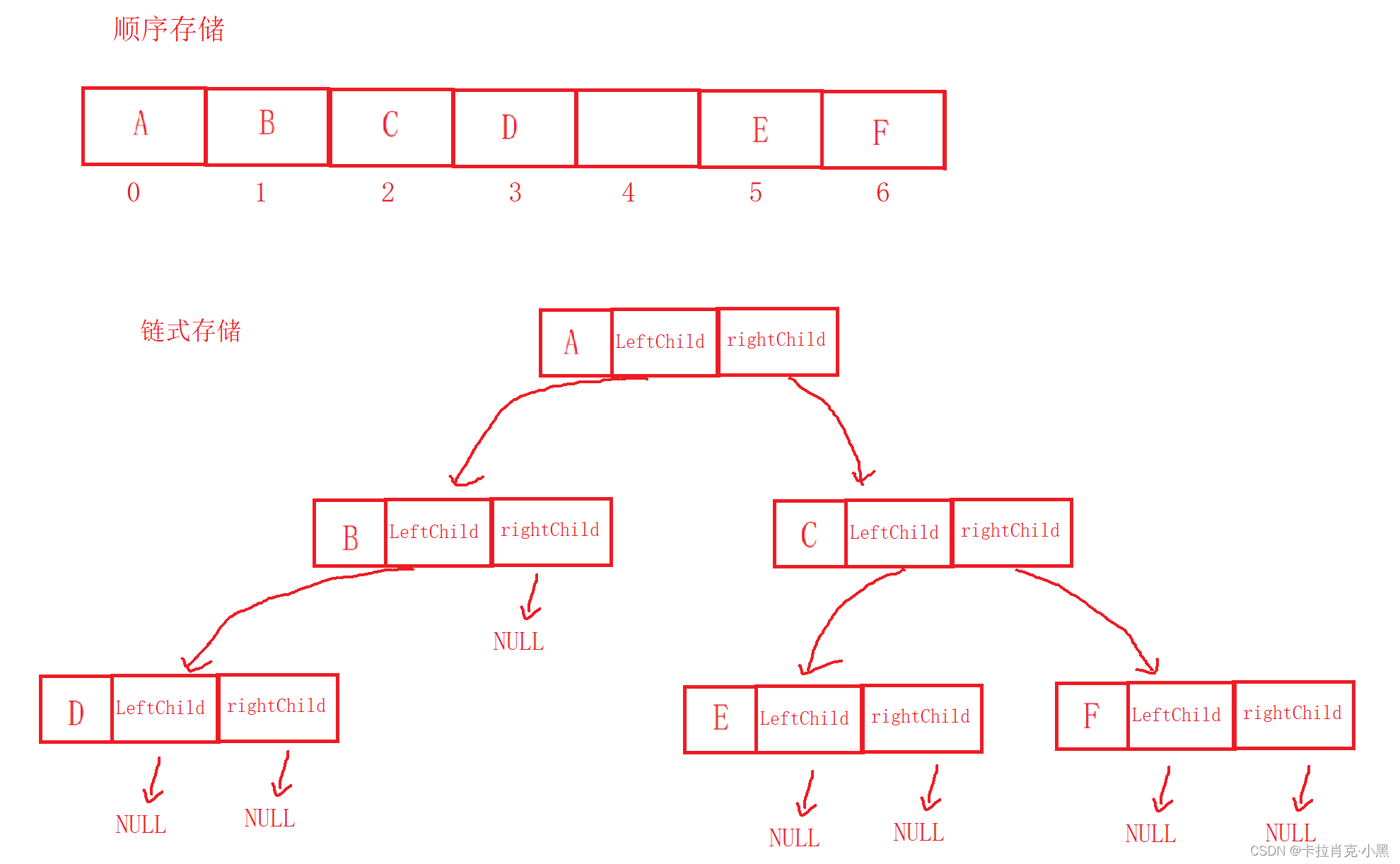
链式存储的结构体如下:
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
三、平衡二叉树实现
1.创建树和树的前中后遍历
1.前中后遍历
所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。
前序遍历:根,左子树,右子树
中序遍历:左子树,根,右子树
后序遍历:左子树,右子树根,

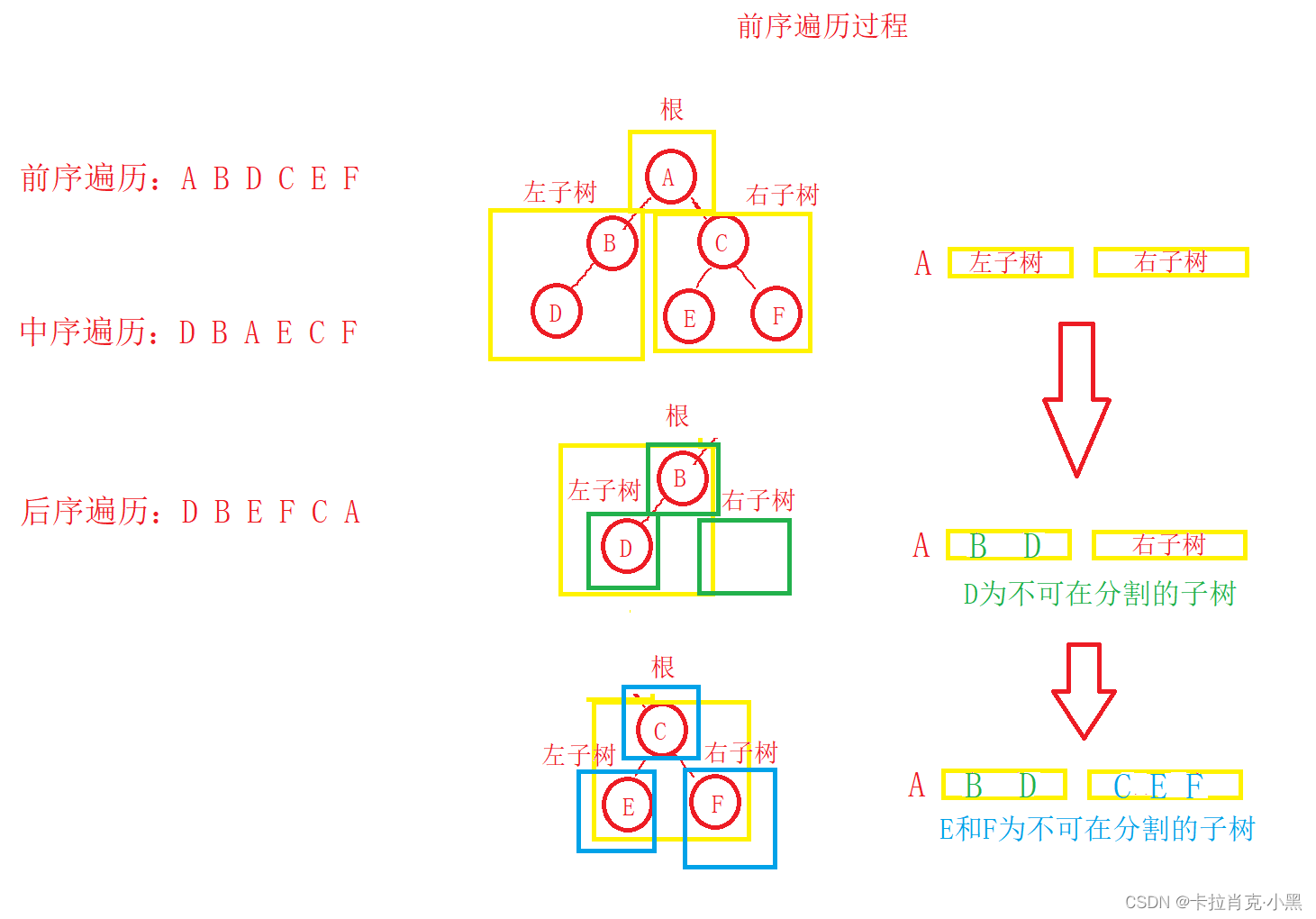
中序和后续的遍历同理。
2.创建树且打印前中后遍历
要实现的函数:
//创建二叉树
void TreeCreate(BTDataType* a, int n);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 二叉树销毁
void BinaryTreeDestory(BTNode** root);
实现代码如下:
//创建二叉树
void TreeCreate(BTNode** root ,BTDataType num)
{if (*root == NULL)//如果节点为空证明该位置为要插入的位置{BTNode* pos = (BTNode*)malloc(sizeof(BTNode));//开辟节点if (pos == NULL)//判断节点是否开辟成功{perror("malloc");exit(-1);}pos->data = num;pos->left = NULL;pos->right = NULL;*root = pos;//把该节点连接到树上return;}if (num < (*root)->data)//比根节点小则在左边插入{TreeCreate(&(*root)->left, num);}else//比根节点大则在右边插入{TreeCreate(&(*root)->right, num);}
}
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){return;}printf("%d ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){return;}BinaryTreeInOrder(root->left);printf("%d ", root->data);BinaryTreeInOrder(root->right);
}
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){return;}BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%d ", root->data);
}
// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{if (*root == NULL){return;}BinaryTreeDestory(&(*root)->left);BinaryTreeDestory(&(*root)->right);free(*root);
}
测试函数:
void test()
{int arr[] = { 2,1,3,7,6,5,9,8,4 };int size = sizeof(arr) / sizeof(arr[0]);BTNode* root = NULL;int i = 0;for (i = 0; i < size; i++){TreeCreate(&root, arr[i]);//创建二叉树}BinaryTreePrevOrder(root);//前printf("\n");BinaryTreeInOrder(root);//中printf("\n");BinaryTreePostOrder(root);//后printf("\n");BinaryTreeDestory(&root);//销毁
}
int main()
{test();return 0;
}
构建的二叉树如下:

前序递归部分过程如下:
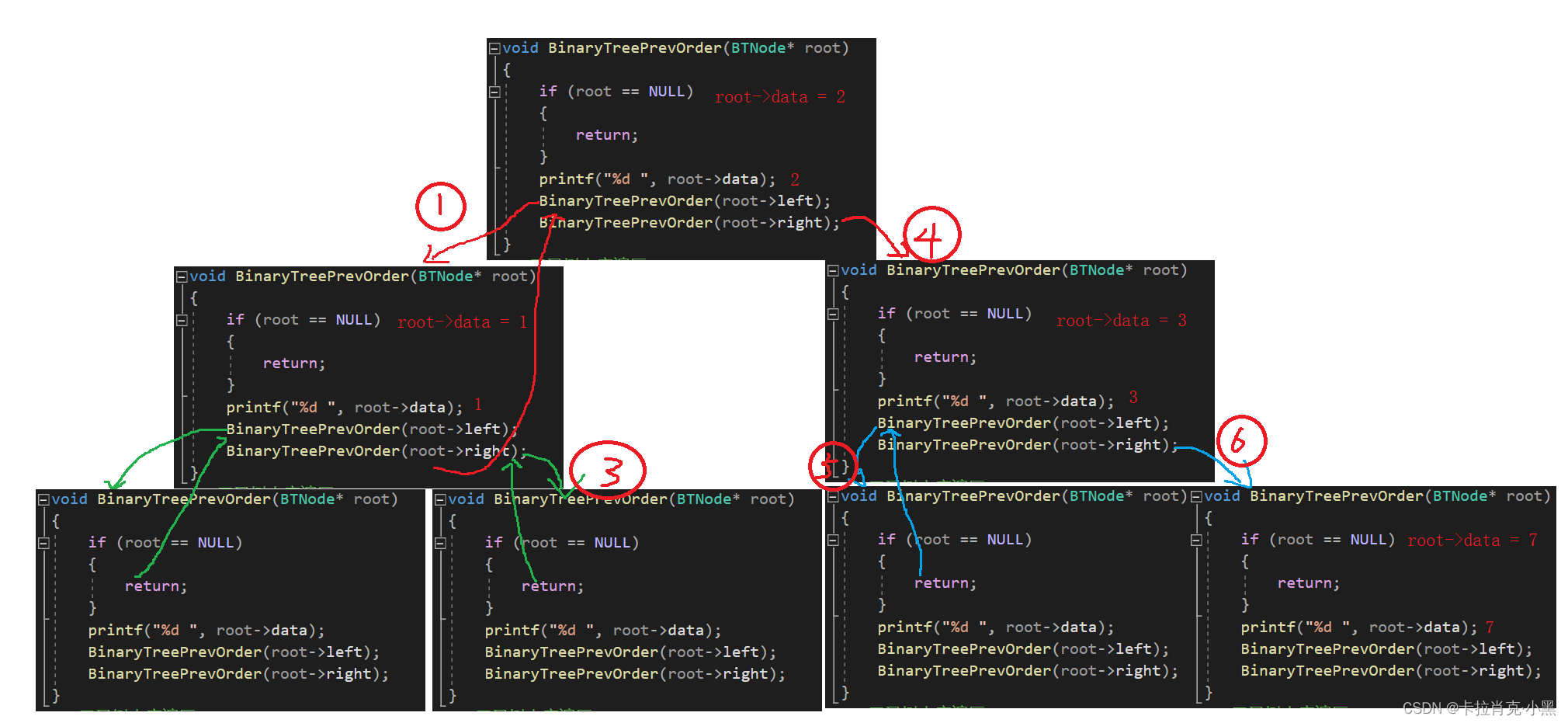
前序要先打印根节点的值在进行递归,中序要先进行左递归,在打印值,最后进行右递归,而后续则是先进行左右递归在打印相应的值。
注意:销毁二叉树要进行后续遍历,只有把根的左右子树都进行释放,才可以释放根节点。根节点先于左右子树释放会找不到相应左右节点,造成内存泄漏。
2.转换为平衡二叉树和相关操作
我们刚才构建的树明显一边节点多,一边节点少,所以我们把上面的树转化为左右子树的节点相差在1以内,进行左右平衡
1.转换为平衡二叉树
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}return BinaryTreeSize(root->left) + 1 + BinaryTreeSize(root->right);
}
//左旋
BTNode* get_min(BTNode* root)
{if (root->left == NULL){return root;}return get_min(root->left);//返回最左边的节点
}
void turn_left(BTNode** root)
{BTNode* pos = *root;(*root) = pos->right;//更换头节点pos->right = NULL;//避免出现野指针get_min(*root)->left = pos;//把最左边的节点链接此接点
}
//右旋
BTNode* get_max(BTNode* root)
{if (root->right == NULL){return root;}return get_max(root->right);//返回最右边的节点
}
void turn_right(BTNode** root)
{BTNode* pos = *root;(*root) = pos->left;pos->left = NULL;get_max(*root)->right = pos;//把最右边的节点链接此接点
}
//转换为平衡二叉树
void BalanceTree(BTNode** root)
{if (*root == NULL){return;}while(1){int a = BinaryTreeSize((*root)->left);int b = BinaryTreeSize((*root)->right);int num = BinaryTreeSize((*root)->left) - BinaryTreeSize((*root)->right);if (num < -1)//右边多{//&(*root)中&和*抵消了,所以传一个root就可以了,但接收要用二级指针turn_left(root);//进行左旋}else if (num > 1)//左边多{turn_right(root);//进行右旋}else{break;}}BalanceTree(&(*root)->left);//开始平衡左子树BalanceTree(&(*root)->right);//开始平衡右子树
}
我们需要对树进行判断是否平衡,就需要求出左右节点的个数,我们还要对左边节点数量大于右边节点数量和右边大于左边的情况分别进行左右旋转。
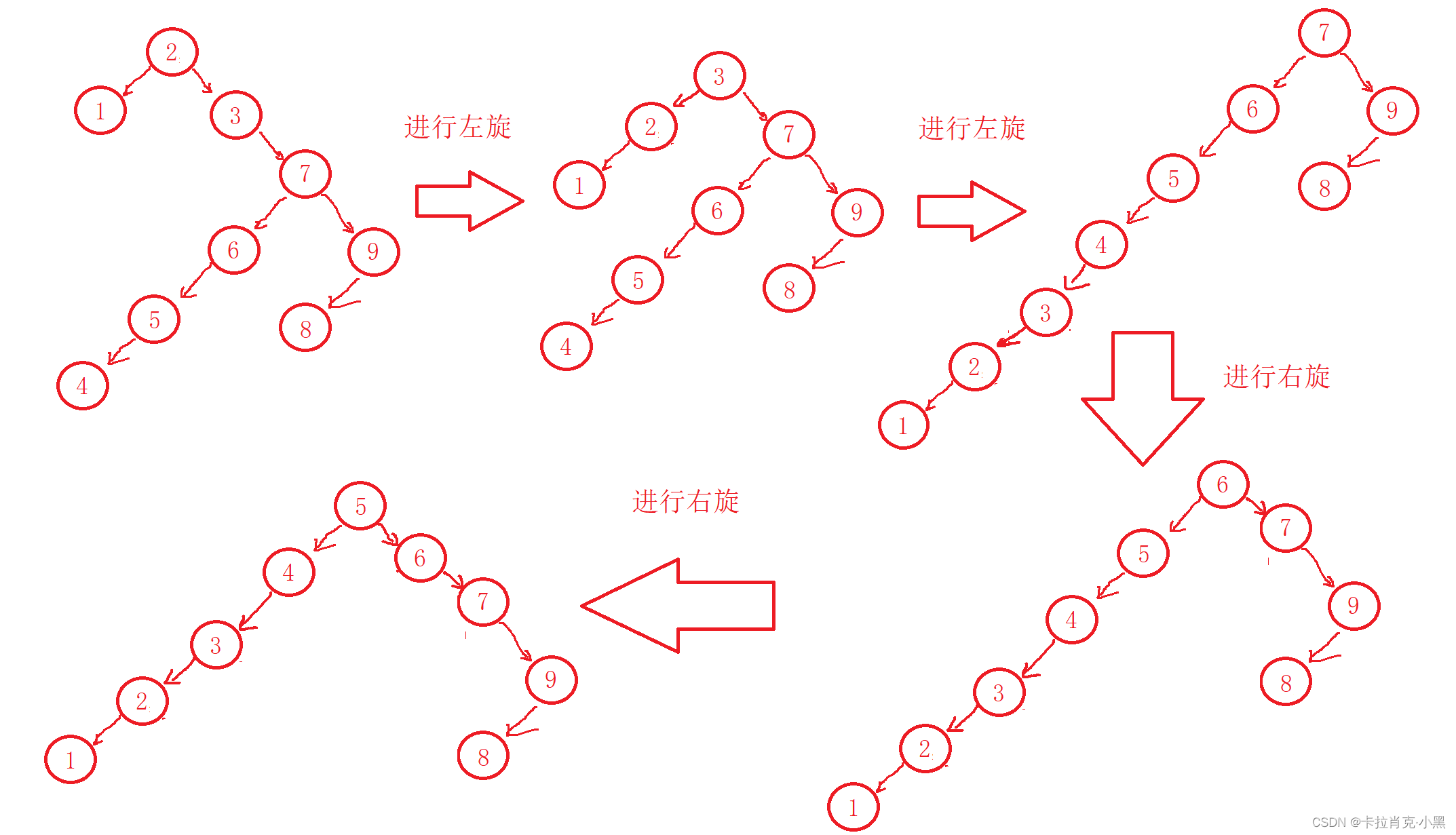
这是进行一次循环,当当前根节点的左右平衡时,开始进行左右子树的平衡。
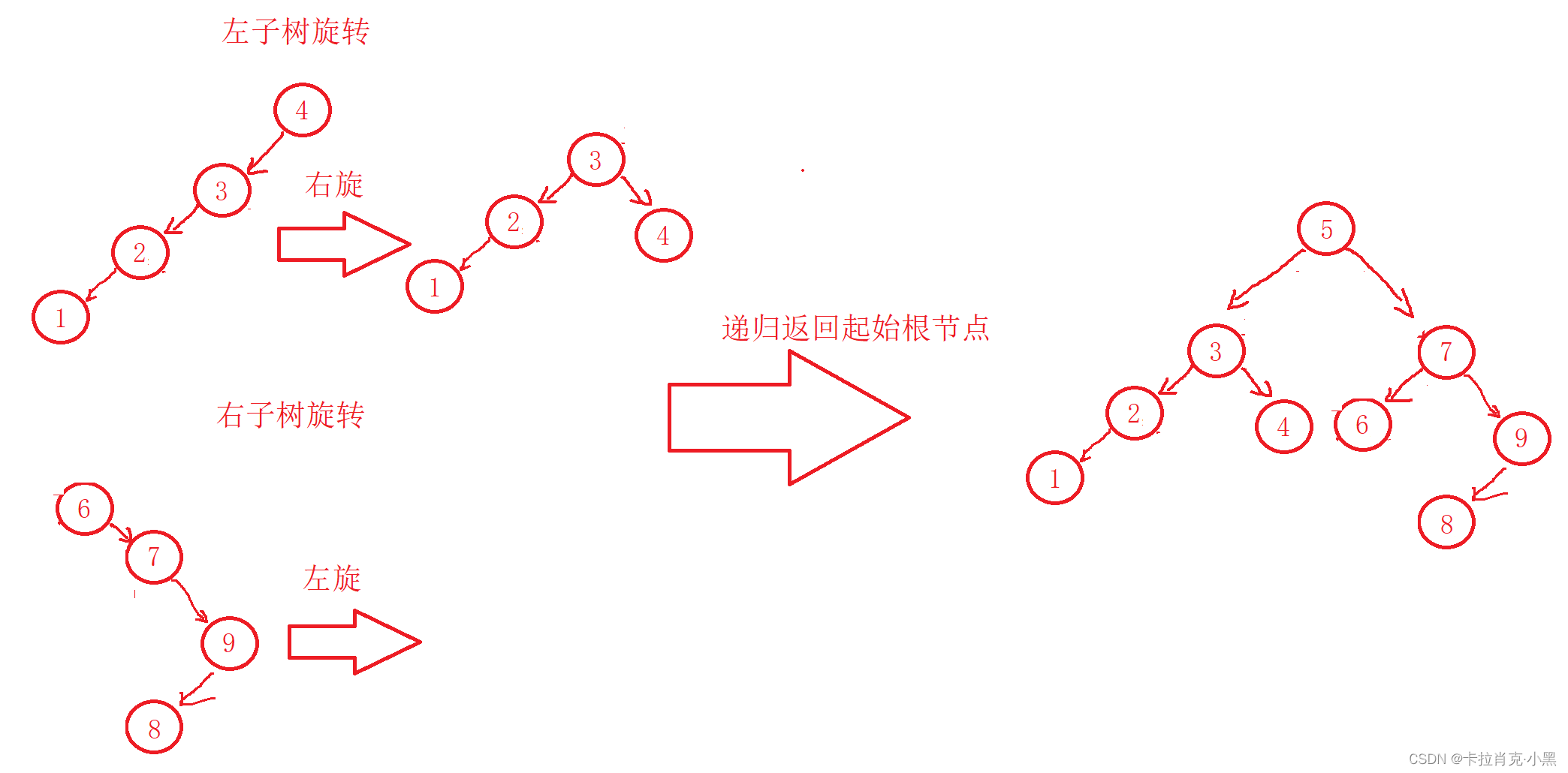
这样我们的平衡树就构建好了。
注意:我们进行左右旋转要连接在最后一个节点上,这样可以保障我们旋转后依然有序,左子树的结果比根节点小,右子树节点比根节点大。
2.二叉树的层序遍历
层序遍历就是按照层来访问二叉树的节点
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{Queue qu;//创建队列QueueInit(&qu);//初始化队列QueuePush(&qu, root);//把根节点带入while (!QueueEmpty(&qu))//如果不为空则一直进行循环{BTNode*pos = QueueFront(&qu);// 获取队列头部元素 printf("%d ", pos->data);QueuePop(&qu);//头部元素出队列if(pos->left != NULL)//如果左孩子不为空则进队列QueuePush(&qu, pos->left);if (pos->right != NULL)//如果右孩子不为空则进队列QueuePush(&qu, pos->right);}QueueDestroy(&qu);
}
层序遍历需要我们用队列进行辅助操作
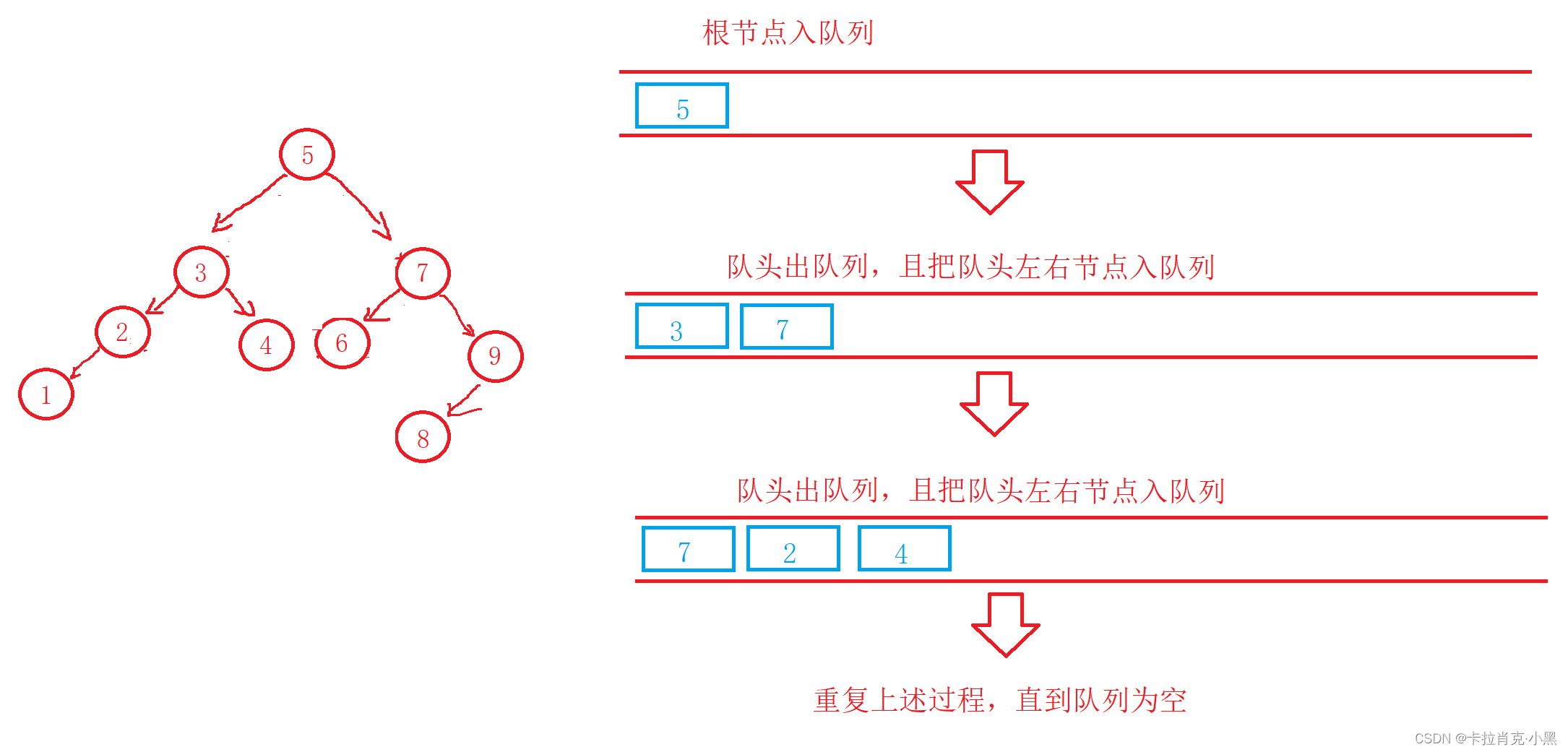
层序遍历需要我们用队列进行辅助操作,由父节点来带动子节点,当子节点不为空就进入队列。
测试代码:
void test()
{int arr[] = { 2,1,3,7,6,5,9,8,4 };int size = sizeof(arr) / sizeof(arr[0]);BTNode* root = NULL;int i = 0;for (i = 0; i < size; i++){TreeCreate(&root, arr[i]);//创建二叉树}BalanceTree(&root);//构建BinaryTreeLevelOrder(root);//层BinaryTreeDestory(&root);//销毁
}
int main()
{test();return 0;
}
3.判断是否为完全二叉树
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Queue qu;//创建队列QueueInit(&qu);//初始化队列QueuePush(&qu, root);//把根节点带入while (!QueueEmpty(&qu))//如果不为空则一直进行循环{BTNode* pos = QueueFront(&qu);// 获取队列头部元素 QueuePop(&qu);//头部元素出队列if (pos != NULL){QueuePush(&qu, pos->left);QueuePush(&qu, pos->right);}else{while (!QueueEmpty(&qu))//一直出队列,直到队列为空停止循环{pos = QueueFront(&qu);// 获取队列头部元素 if (pos != NULL)//如果头部不为空,则证明不为完全二叉树{QueueDestroy(&qu);//销毁队列return false;}QueuePop(&qu);//头部元素出队列}}}QueueDestroy(&qu);return true;
}
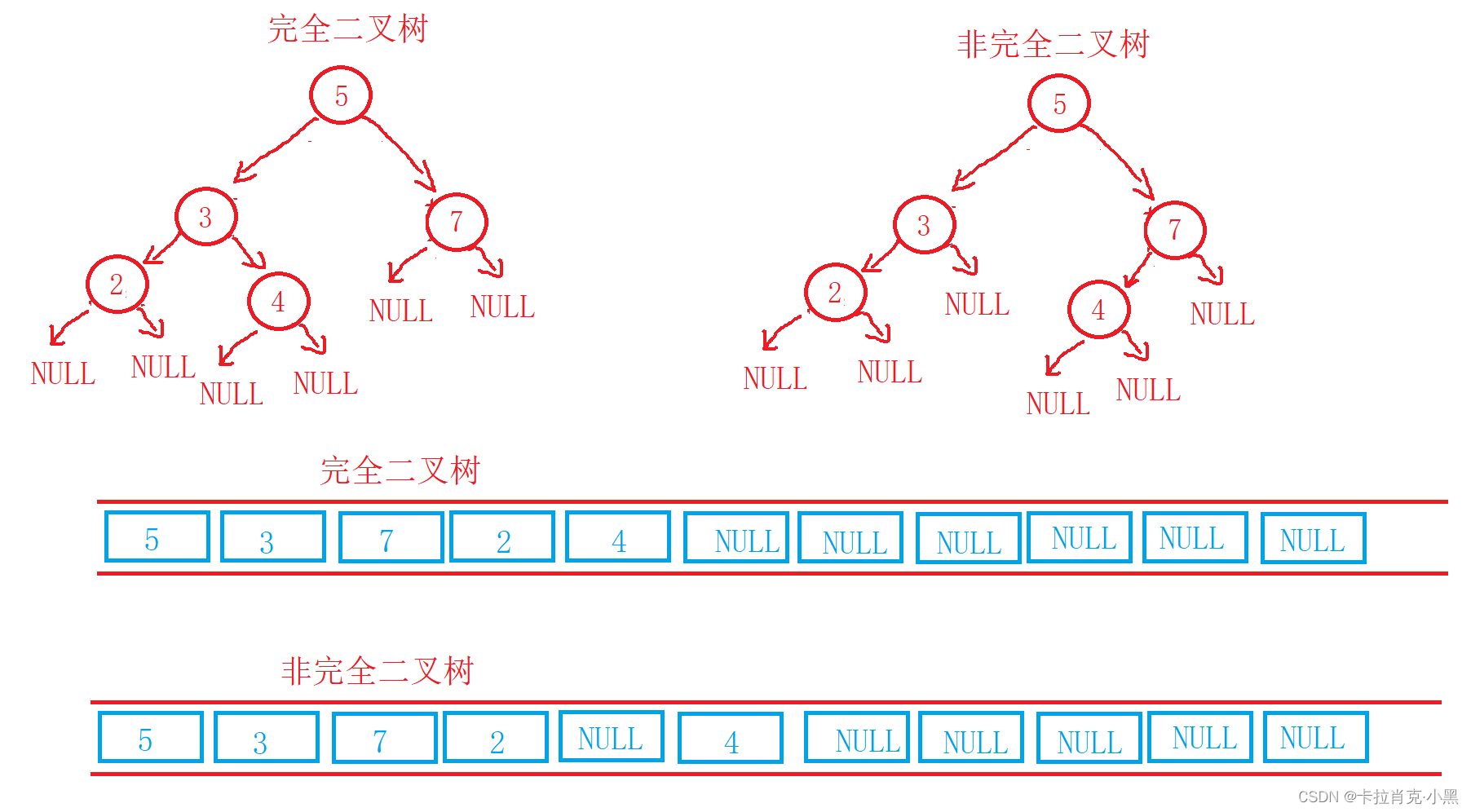
判断是否为完全二叉树也需要用到队列,当为完全二叉树时,队列不会出现数据和空交替出队列的情况,而非完全二叉树会出现数据和空交替出队列的情况
测试代码如下:
void test()
{int arr[] = { 2,1,3,7,6,5,9,8,4 };int size = sizeof(arr) / sizeof(arr[0]);BTNode* root = NULL;int i = 0;for (i = 0; i < size; i++){TreeCreate(&root, arr[i]);//创建二叉树}BalanceTree(&root);//构建if (BinaryTreeComplete(root))//完全{printf("YES\n");}else{printf("NO\n");}BinaryTreeDestory(&root);//销毁
}
int main()
{test();return 0;
}

4.平衡二叉树的节点删除
//删除头节点,可以改为按查找节点删除
void DelTree(BTNode** root)//进行左旋
{BTNode* del = *root;//保存要删除的元素节点*root = del->left;//更换头节点get_max(*root)->right = del->right;free(del);BalanceTree(root);//从新构建平衡树
}
我们选择的是删除头根节点,然后进行左旋,从新构建成树,在进行平衡树的构建。我们也可以选择删除指定的节点,树的节点删除一般没有意义。
过程如下:
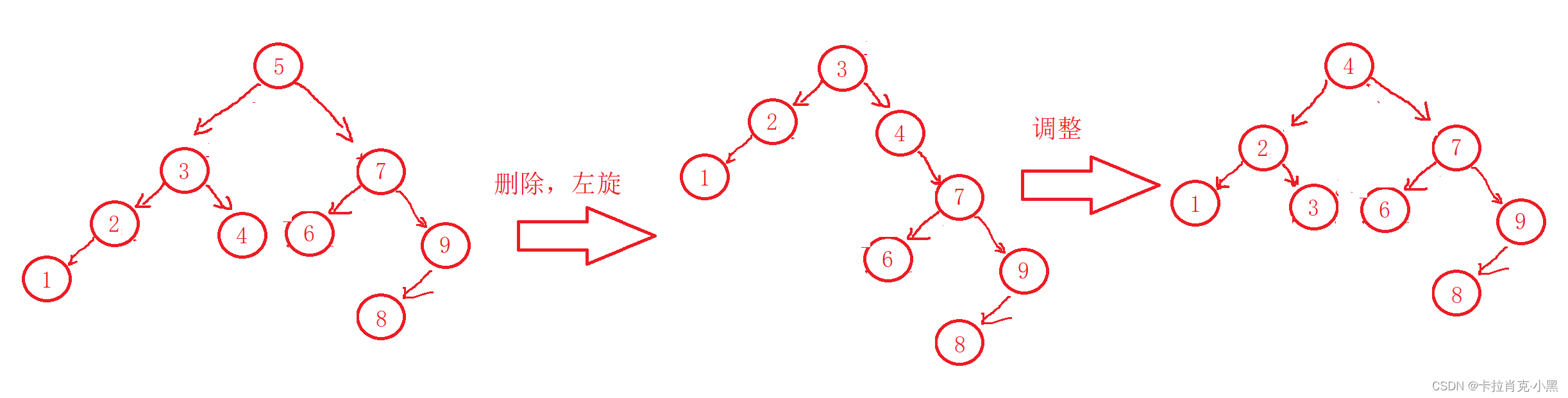
3.二叉树其他操作
// 二叉树最深节点
int DeepTree(BTNode* root)
{if (root == NULL){return 0;}//三目表达式,返回左子树和右子树最大的那个return DeepTree(root->left) > DeepTree(root->right) ? DeepTree(root->left) + 1 : DeepTree(root->right) + 1;
}
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)//当该节点为空时返回上一级,证明上一级左子树或右子树有一个不为空{return 0;}if (root->left == NULL && root->right == NULL)//当左右子树都为空时这个节点为叶子节点{return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);//返回左右子树的总和}
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (k == 1)//从第一层开始,所以递减到1就可以了{return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);//返回左右子树的总和
}
// 二叉树查找值为x的节点
//BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
//{
// if (root == NULL)//如果没找到则返回空
// {
// return NULL;
// }
// if (root->data == x)
// {
// return root;
// }
// BTNode* left = BinaryTreeFind(root->left, x);
// BTNode* right = BinaryTreeFind(root->right, x);
// if (left == NULL)//如果左子树没找到该值,则返回右子树的值,右子树树中也没找到返回的空,找到则返回相应的节点
// {
// return right;
// }
// return left;//要找的节点在左子树上
//}
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{BTNode* pos = root;while (pos != NULL){if (pos->data < x)//该节点的值小于查找的值则在树的右边{pos = pos->right;}else if(pos->data > x)//该节点的值大于查找的值则在树的左边{pos = pos->left;}else{break;}}return pos;
}
二叉树节点的查找可以用正常方式的查找,也可以针对我们所构建的平衡二叉树设计一个函数,我们所设计的平衡二叉树的节点都满足左孩子的值小于父节点的值,右孩子的值都大于父节点的值,这样设计便于我们进行查找。
测试函数:
void test()
{int arr[] = { 2,1,3,7,6,5,9,8,4 };int size = sizeof(arr) / sizeof(arr[0]);BTNode* root = NULL;int i = 0;for (i = 0; i < size; i++){TreeCreate(&root, arr[i]);//创建二叉树}BalanceTree(&root);//构建printf("%d\n", DeepTree(root));//深度printf("%d\n", BinaryTreeLeafSize(root));//节点个数printf("%d\n", BinaryTreeLevelKSize(root,3));//k层printf("%d\n", BinaryTreeFind(root,3)->data);//查找节点BinaryTreeDestory(&root);//销毁
}
int main()
{test();return 0;
}

总结
树的更加高阶的内容我们会在进一步的学习中逐步的解锁
下面是本次的全部代码:
main.c:
#include"main.h"
void test()
{int arr[] = { 2,1,3,7,6,5,9,8,4 };int size = sizeof(arr) / sizeof(arr[0]);BTNode* root = NULL;int i = 0;for (i = 0; i < size; i++){TreeCreate(&root, arr[i]);//创建二叉树}BinaryTreePrevOrder(root);//前printf("\n");BinaryTreeInOrder(root);//中printf("\n");BinaryTreePostOrder(root);//后printf("\n");printf("%d", BinaryTreeSize(root));//节点个数printf("\n");BalanceTree(&root);//构建BinaryTreeLevelOrder(root);//层printf("\n");if (BinaryTreeComplete(root))//完全{printf("YES\n");}else{printf("NO\n");}printf("%d\n", DeepTree(root));//深度printf("%d\n", BinaryTreeLeafSize(root));//节点个数printf("%d\n", BinaryTreeLevelKSize(root,3));//k层printf("%d\n", BinaryTreeFind(root,3)->data);//查找节点DelTree(&root);BinaryTreeLevelOrder(root);//层BinaryTreeDestory(&root);//销毁
}
int main()
{test();return 0;
}
main.h:
#pragma once
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
// 链式结构:表示队列
typedef BTNode* QDataType;
typedef struct QListNode
{struct QListNode* next;QDataType data;
}QNode;
// 队列的结构
typedef struct Queue
{QNode* front;QNode* rear;
}Queue;
// 初始化队列
void QueueInit(Queue* q);
// 队尾入队列
void QueuePush(Queue* q, QDataType data);
// 队头出队列
void QueuePop(Queue* q);
// 获取队列头部元素
QDataType* QueueFront(Queue* q);
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool QueueEmpty(Queue* q);
// 销毁队列
void QueueDestroy(Queue* q);
//创建二叉树
void TreeCreate(BTDataType* a, int n);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 二叉树销毁
void BinaryTreeDestory(BTNode** root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
//转换为平衡二叉树
void BalanceTree(BTNode** root);
//删除头节点
void DelTree(BTNode** root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root);
// 二叉树最深节点
int DeepTree(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
test.c:
#include"main.h"// 初始化队列
void QueueInit(Queue* q)
{assert(q);q->front = q->rear = NULL;
}
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{assert(q);QNode* pos = (QNode*)malloc(sizeof(QNode));if (pos == NULL){perror("malloc");exit(-1);}pos->data = data;pos->next = NULL;if (q->rear == NULL){q->front = q->rear = pos;}else{q->rear->next = pos;q->rear = pos;}
}
// 队头出队列
void QueuePop(Queue* q)
{assert(q);assert(q->front);if (q->front->next == NULL){free(q->front);q->front = q->rear = NULL;}else{QNode* next = q->front->next;free(q->front);q->front = next;}
}
// 获取队列头部元素
QDataType* QueueFront(Queue* q)
{assert(q);assert(q->front);return q->front->data;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool QueueEmpty(Queue* q)
{assert(q);return q->front == NULL;
}
// 销毁队列
void QueueDestroy(Queue* q)
{assert(q);QNode* pos = q->front;while (pos){QNode* next = pos->next;free(pos);pos = next;}q->front = q->rear = NULL;
}
//创建二叉树
void TreeCreate(BTNode** root ,BTDataType num)
{if (*root == NULL)//如果节点为空证明该位置为要插入的位置{BTNode* pos = (BTNode*)malloc(sizeof(BTNode));//开辟节点if (pos == NULL)//判断节点是否开辟成功{perror("malloc");exit(-1);}pos->data = num;pos->left = NULL;pos->right = NULL;*root = pos;//把该节点连接到树上return;}if (num < (*root)->data)//比根节点小则在左边插入{TreeCreate(&(*root)->left, num);}else//比根节点大则在右边插入{TreeCreate(&(*root)->right, num);}
}
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){return;}printf("%d ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){return;}BinaryTreeInOrder(root->left);printf("%d ", root->data);BinaryTreeInOrder(root->right);
}
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){return;}BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%d ", root->data);
}
// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{if (*root == NULL){return;}BinaryTreeDestory(&(*root)->left);BinaryTreeDestory(&(*root)->right);free(*root);
}
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}return BinaryTreeSize(root->left) + 1 + BinaryTreeSize(root->right);
}
//左旋
BTNode* get_min(BTNode* root)
{if (root->left == NULL){return root;}return get_min(root->left);//返回最左边的节点
}
void turn_left(BTNode** root)
{BTNode* pos = *root;(*root) = pos->right;//更换头节点pos->right = NULL;//避免出现野指针get_min(*root)->left = pos;//把最左边的节点链接此接点
}
//右旋
BTNode* get_max(BTNode* root)
{if (root->right == NULL){return root;}return get_max(root->right);//返回最右边的节点
}
void turn_right(BTNode** root)
{BTNode* pos = *root;(*root) = pos->left;pos->left = NULL;get_max(*root)->right = pos;//把最右边的节点链接此接点
}
//转换为平衡二叉树
void BalanceTree(BTNode** root)
{if (*root == NULL){return;}while(1){int a = BinaryTreeSize((*root)->left);int b = BinaryTreeSize((*root)->right);int num = BinaryTreeSize((*root)->left) - BinaryTreeSize((*root)->right);if (num < -1)//右边多{//&(*root)中&和*抵消了,所以传一个root就可以了,但接收要用二级指针turn_left(root);//进行左旋}else if (num > 1)//左边多{turn_right(root);//进行右旋}else{break;}}BalanceTree(&(*root)->left);//开始平衡左子树BalanceTree(&(*root)->right);//开始平衡右子树
}
//删除头节点,可以改为按查找节点删除
void DelTree(BTNode** root)//进行左旋
{BTNode* del = *root;//保存要删除的元素节点*root = del->left;//更换头节点get_max(*root)->right = del->right;free(del);BalanceTree(root);//从新构建平衡树
}
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{Queue qu;//创建队列QueueInit(&qu);//初始化队列QueuePush(&qu, root);//把根节点带入while (!QueueEmpty(&qu))//如果不为空则一直进行循环{BTNode*pos = QueueFront(&qu);// 获取队列头部元素 printf("%d ", pos->data);QueuePop(&qu);//头部元素出队列if(pos->left != NULL)//如果左孩子不为空则进队列QueuePush(&qu, pos->left);if (pos->right != NULL)//如果右孩子不为空则进队列QueuePush(&qu, pos->right);}QueueDestroy(&qu);
}
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Queue qu;//创建队列QueueInit(&qu);//初始化队列QueuePush(&qu, root);//把根节点带入while (!QueueEmpty(&qu))//如果不为空则一直进行循环{BTNode* pos = QueueFront(&qu);// 获取队列头部元素 QueuePop(&qu);//头部元素出队列if (pos != NULL){QueuePush(&qu, pos->left);QueuePush(&qu, pos->right);}else{while (!QueueEmpty(&qu))//一直出队列,直到队列为空停止循环{pos = QueueFront(&qu);// 获取队列头部元素 if (pos != NULL)//如果头部不为空,则证明不为完全二叉树{QueueDestroy(&qu);//销毁队列return false;}QueuePop(&qu);//头部元素出队列}}}QueueDestroy(&qu);return true;
}
// 二叉树最深节点
int DeepTree(BTNode* root)
{if (root == NULL){return 0;}//三目表达式,返回左子树和右子树最大的那个return DeepTree(root->left) > DeepTree(root->right) ? DeepTree(root->left) + 1 : DeepTree(root->right) + 1;
}
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)//当该节点为空时返回上一级,证明上一级左子树或右子树有一个不为空{return 0;}if (root->left == NULL && root->right == NULL)//当左右子树都为空时这个节点为叶子节点{return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);//返回左右子树的总和}
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (k == 1)//从第一层开始,所以递减到1就可以了{return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);//返回左右子树的总和
}
// 二叉树查找值为x的节点
//BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
//{
// if (root == NULL)//如果没找到则返回空
// {
// return NULL;
// }
// if (root->data == x)
// {
// return root;
// }
// BTNode* left = BinaryTreeFind(root->left, x);
// BTNode* right = BinaryTreeFind(root->right, x);
// if (left == NULL)//如果左子树没找到该值,则返回右子树的值,右子树树中也没找到返回的空,找到则返回相应的节点
// {
// return right;
// }
// return left;//要找的节点在左子树上
//}
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{BTNode* pos = root;while (pos != NULL){if (pos->data < x)//该节点的值小于查找的值则在树的右边{pos = pos->right;}else if(pos->data > x)//该节点的值大于查找的值则在树的左边{pos = pos->left;}else{break;}}return pos;
}
相关文章:

数据结构:二叉树及相关操作
文章目录 前言一、树的概念及结构1.什么是树2. 树的相关概念3.树的表示 二、二叉树概念及结构1.二叉树概念2.特殊的二叉树3.二叉树的性质4.二叉树的存储结构 三、平衡二叉树实现1.创建树和树的前中后遍历1.前中后遍历2.创建树且打印前中后遍历 2.转换为平衡二叉树和相关操作1.转…...
4.物联网LWIP之C/S编程,stm32作为服务器,stm32作为客户端,代码的优化
LWIP配置 服务器端实现 客户端实现 错误分析 一。LWIP配置(FREERTOS配置,ETH配置,LWIP配置) 1.FREERTOS配置 为什么要修改定时源为Tim1?不用systick? 原因:HAL库与FREERTOS都需要使用systi…...

【C语言】扫雷游戏(可展开)——超细教学
🚩纸上得来终觉浅, 绝知此事要躬行。 🌟主页:June-Frost 🚀专栏:C语言 🔥该篇将运用数组来实现 扫雷游戏。 目录: 🌟思路框架测试游戏 🌟测试部分函数实现&am…...

数据的深海潜行:数据湖、数据仓库与数据湖库之间的微妙关系
导言:数据的重要性与存储挑战 在这个信息爆炸的时代,数据已经成为企业的核心资产,而如何高效、安全、便捷地存储这些数据,更是每个组织面临的重大挑战。 数据作为组织的核心资产 数据在过去的几十年里从一个辅助工具演变成企业的…...
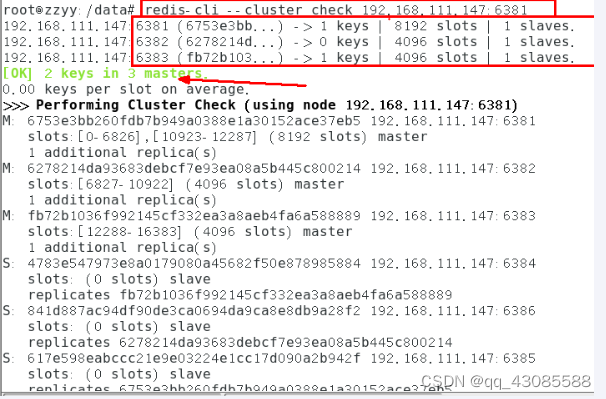
Docker 安装 Redis集群
1. 面试题 1.1 1~2亿条数据需要缓存,请问如何设计这个存储案例 单机单台不可能实现,肯定是用分布式存储,用redis如何落地? 1.2 上述问题工程案例场景设计类题目,解决方案 1.2.1 哈希取余分区 2亿条记录就是2亿个k,v&…...
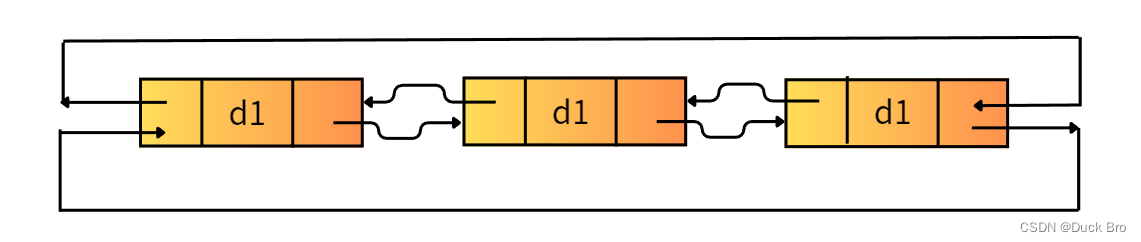
数据结构入门 — 链表详解_单链表
前言 数据结构入门 — 单链表详解* 博客主页链接:https://blog.csdn.net/m0_74014525 关注博主,后期持续更新系列文章 文章末尾有源码 *****感谢观看,希望对你有所帮助***** 系列文章 第一篇:数据结构入门 — 链表详解_单链表 第…...

从零学算法151
151.给你一个字符串 s ,请你反转字符串中 单词 的顺序。 单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。 返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。 注意:输入字符串 s中可能会存在前导空格、尾随…...

【Vue】动态设置元素类以及样式
Vue2 动态设置元素类以及样式 1.动态设置类 class 1.1 字符串语法 通过v-bind绑定元素的class属性,为其指定一个字符串: <div v-bind:class"className">class动态绑定</div> <script> export default {data() {return {…...
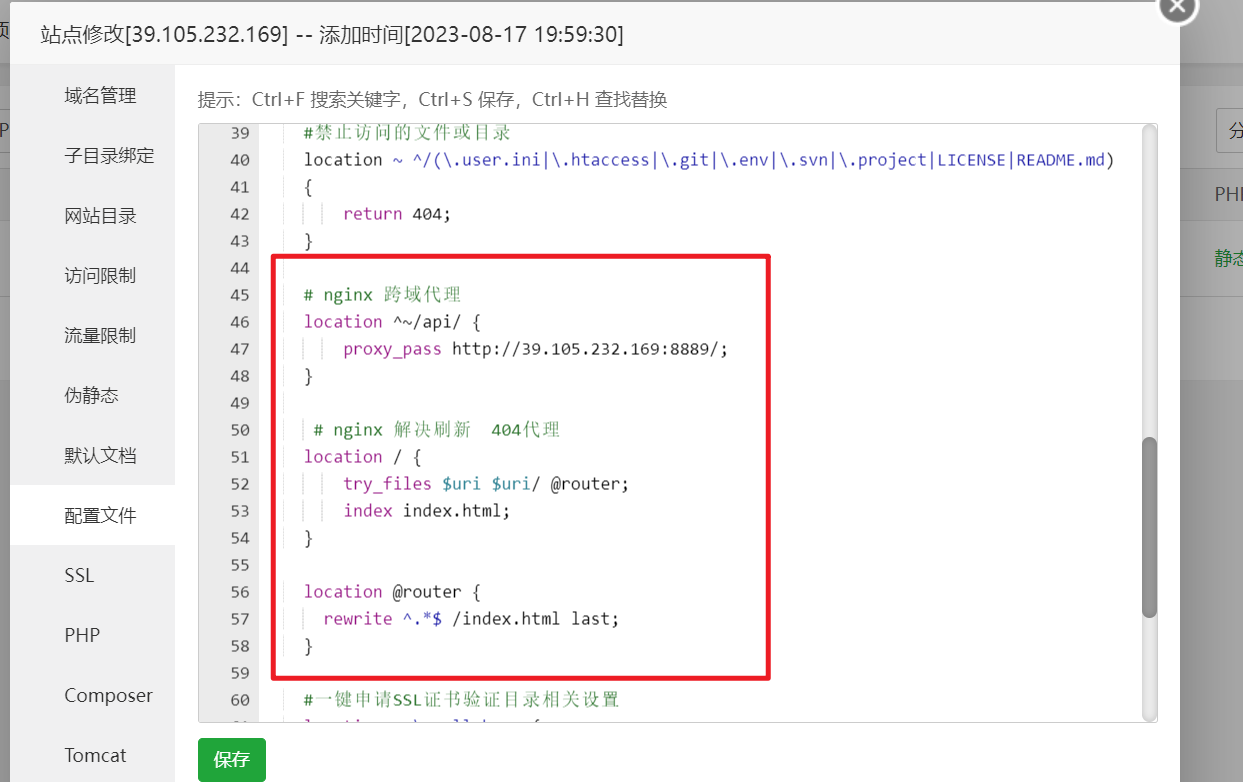
node和前端项目宝塔部署
首先需要一台服务器 购买渠道:阿里云、腾讯云、百度云、华为云 一、以阿里云为例 购买esc 可临时购买测试服务器 二、安装宝塔 复制公网ip地址 通过Xshell 进行账号密码的连接 连接后访问宝塔官网 宝塔面板下载,免费全能的服务器运维软件 找到自己…...

【Python原创毕设|课设】基于Python Flask的上海美食信息与可视化宣传网站项目-文末附下载方式以及往届优秀论文,原创项目其他均为抄袭
基于Python Flask的上海美食信息与可视化宣传网站(获取方式访问文末官网) 一、项目简介二、开发环境三、项目技术四、功能结构五、运行截图六、功能实现七、数据库设计八、源码获取 一、项目简介 随着大数据和人工智能技术的迅速发展,我们设…...

【HTML】HTML面试知识梳理
目录 DOCTYPE(文章类型)head标签浏览器乱码的原因及解决常用的meta标签与SEOscript标签中defer和async的区别src&href区别HTML5有哪些更新语义化标签媒体标签表单进度条、度量器DOM查询Web存储Canvas和SVG拖放 (HTML5 drag API࿰…...

Java进阶篇--IO流的第二篇《多样的流》
目录 Java缓冲流 BufferedReader和BufferedWriter类 Java随机流 Java数组流 字节数组流 ByteArrayInputStream流的构造方法: ByteArrayOutputStream流的构造方法: 字符数组流 Java数据流 Java对象流 Java序列化与对象克隆 扩展小知识&#x…...
iPhone 14 Pro 动态岛的功能和使用方法详解
当iPhone 14 Pro机型发布时,苹果公司将软件功能与屏幕顶部的药丸状切口创新集成,称之为“灵动岛”,这让许多人感到惊讶。这篇文章解释了它的功能、工作原理,以及你如何与它互动以执行动作。 一、什么是灵动岛?它是如何工作的 在谣言周期的早期iPhone 14 Pro 在宣布时…...

掌握这20条你将超过90%的测试员
1、不断学习 不管是“软技能”,比如公开演讲, 或者编程语言,亦或新的测试技术,成功的软件测试工程师总是会从繁忙中抽出时间来坚持学习。 2、管理你的时间 我们的时间很容易被大块的工作和不断的会议所占据,导致我们…...

LightDB create table时列约束支持enable/disable关键字
功能介绍 为了方便用户从Oracle数据库迁移到LightDB数据库,LightDB从23.3版本开始支持 create table时列约束支持enable/disable关键字。这个功能仅是语法糖。 使用说明 执行create table时,列约束后面可以选择性添加enable/disable关键字。 create …...

使用BeeWare实现iOS调用Python
1、准备工作 1.1、安装Python 1.2、设置虚拟环境 我们现在将创建一个虚拟环境——一个“沙盒”,如果我们将软件包安装到虚拟环境中,我们计算机上的任何其他Python项目将不会受到影响。如果我们把虚拟环境搞得一团糟,我们将能够简单地删除它…...
无公网IP内网穿透使用vscode配置SSH远程ubuntu随时随地开发写代码
文章目录 前言1、安装OpenSSH2、vscode配置ssh3. 局域网测试连接远程服务器4. 公网远程连接4.1 ubuntu安装cpolar内网穿透4.2 创建隧道映射4.3 测试公网远程连接 5. 配置固定TCP端口地址5.1 保留一个固定TCP端口地址5.2 配置固定TCP端口地址5.3 测试固定公网地址远程 前言 远程…...
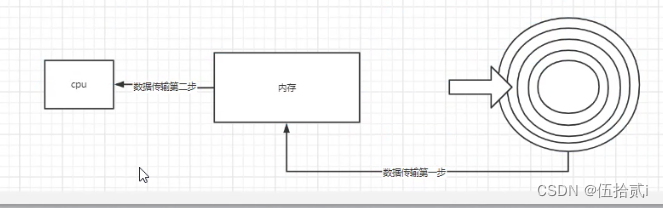
二叉树、红黑树、B树、B+树
二叉树 一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。 二叉树的特点: 每个结点最多有两棵子树,即二叉树不存在度大于2的结点。二叉树的子树有左右之分…...

12,【设计模式】工厂
设计模式工厂 通过工程来构建任意参数对象&&std::forwardstd::move 在C中,“工厂”(Factory)是一种设计模式,它提供了一种创建对象的方式,将对象的创建和使用代码分离开来,提高了代码的可扩展性和可…...
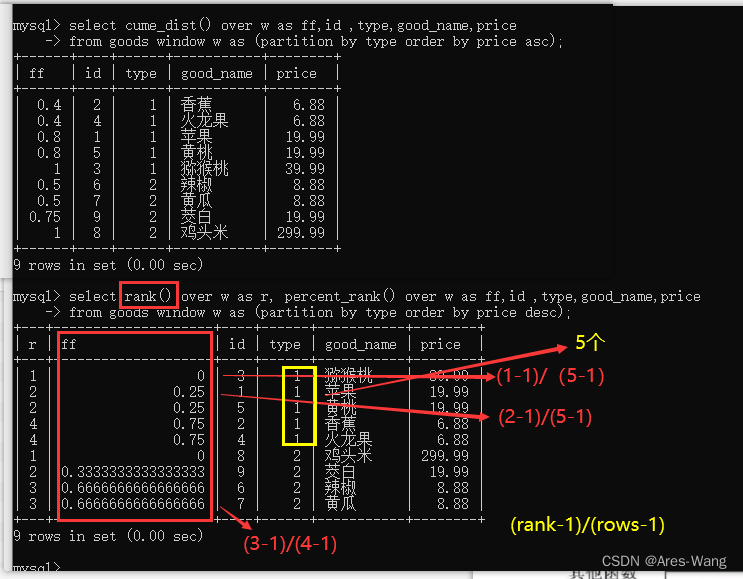
mysql 8.0 窗口函数 之 分布函数 与 sql server (2017以后支持) 分布函数 一样
mysql 分布函数 percent_rank() :等级值 百分比cume_dist() :累积分布值 percent_rank() 计算方式 (rank-1)/(rows-1), 其中 rank 的值为使用RANK()函数产生的序号,rows 的值为当前…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...
