算法leetcode|72. 编辑距离(rust重拳出击)
文章目录
- 72. 编辑距离:
- 样例 1:
- 样例 2:
- 提示:
- 分析:
- 题解:
- rust:
- 二维数组(易懂)
- 滚动数组(更加优化的内存空间)
- go:
- c++:
- python:
- java:
72. 编辑距离:
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
样例 1:
输入:word1 = "horse", word2 = "ros"输出:3解释:horse -> rorse (将 'h' 替换为 'r')rorse -> rose (删除 'r')rose -> ros (删除 'e')
样例 2:
输入:word1 = "intention", word2 = "execution"输出:5解释:intention -> inention (删除 't')inention -> enention (将 'i' 替换为 'e')enention -> exention (将 'n' 替换为 'x')exention -> exection (将 'n' 替换为 'c')exection -> execution (插入 'u')
提示:
0 <= word1.length, word2.length <= 500word1和word2由小写英文字母组成
分析:
-
面对这道算法题目,二当家的再次陷入了沉思。
-
编辑距离算法在实际应用中还是很多的,比如一些命令的参数,当输入了错误的参数时,会提示最相似的命令。
 - 想要找最优解,一般就是贪心或者动态规划。
- 想要找最优解,一般就是贪心或者动态规划。 -
思考后会发现,完整串的编辑距离和子串的编辑距离有关系,所以考虑使用动态规划。
-
别急,这里还有一个问题,题目中可以对两个单词分别进行三种操作,所以相当于一共有六种操作,其中插入字符依赖较短字符串,而删除字符的操作就反向依赖了较长串,但是动态规划是从一个初识条件开始,朝着一个方向计算的,这里依赖着两种方向,这怎么办?
-
其实,我们可以将相同效果的操作合并处理:
-
对单词 A 删除一个字符和对单词 B 插入一个字符是等价的。例如当单词 A 为 doge,单词 B 为 dog 时,我们既可以删除单词 A 的最后一个字符 e,得到相同的 dog,也可以在单词 B 末尾添加一个字符 e,得到相同的 doge;
-
同理,对单词 B 删除一个字符和对单词 A 插入一个字符也是等价的;
-
对单词 A 替换一个字符和对单词 B 替换一个字符是等价的。例如当单词 A 为 bat,单词 B 为 cat 时,我们修改单词 A 的第一个字母 b -> c,和修改单词 B 的第一个字母 c -> b 是等价的。
-
-
这样一来,本质不同的操作实际上只有三种:
-
在单词 A 中插入一个字符;
-
在单词 B 中插入一个字符;
-
修改单词 A 的一个字符。
-
-
这样一来,我们就可以把原问题转化为规模较小的子问题。以样例1为例,我们用 A = horse,B = ros 作为例子,来看一看是如何把这个问题转化为规模较小的若干子问题的:
-
在单词 A 中插入一个字符:如果我们知道 horse 到 ro 的编辑距离为 a,那么显然 horse 到 ros 的编辑距离不会超过 a + 1。这是因为我们可以在 a 次操作后将 horse 和 ro 变为相同的字符串,只需要额外的 1 次操作,在单词 A 的末尾添加字符 s,就能在 a + 1 次操作后将 horse 和 ro 变为相同的字符串;
-
在单词 B 中插入一个字符:如果我们知道 hors 到 ros 的编辑距离为 b,那么显然 horse 到 ros 的编辑距离不会超过 b + 1,原因同上;
-
修改单词 A 的一个字符:如果我们知道 hors 到 ro 的编辑距离为 c,那么显然 horse 到 ros 的编辑距离不会超过 c + 1,原因同上。
-
-
那么从 horse 变成 ros 的编辑距离应该为 min(a + 1, b + 1, c + 1)。
-
因此,我们就可以使用动态规划来解决这个问题了。我们用 D[i][j] 表示 A 的前 i 个字母和 B 的前 j 个字母之间的编辑距离。
-
如上所述,当我们获得 D[i][j-1],D[i-1][j] 和 D[i-1][j-1] 的值之后就可以计算出 D[i][j]。
-
D[i][j-1] 为 A 的前 i 个字符和 B 的前 j - 1 个字符编辑距离的子问题。即对于 B 的第 j 个字符,我们在 A 的末尾添加了一个相同的字符,那么 D[i][j] 最小可以为 D[i][j-1] + 1;
-
D[i-1][j] 为 A 的前 i - 1 个字符和 B 的前 j 个字符编辑距离的子问题。即对于 A 的第 i 个字符,我们在 B 的末尾添加了一个相同的字符,那么 D[i][j] 最小可以为 D[i-1][j] + 1;
-
D[i-1][j-1] 为 A 前 i - 1 个字符和 B 的前 j - 1 个字符编辑距离的子问题。即对于 B 的第 j 个字符,我们修改 A 的第 i 个字符使它们相同,那么 D[i][j] 最小可以为 D[i-1][j-1] + 1。特别地,如果 A 的第 i 个字符和 B 的第 j 个字符原本就相同,那么我们实际上不需要进行修改操作。在这种情况下,D[i][j] 最小可以为 D[i-1][j-1]。
-
-
一般题解到这里就结束了,但其实我们还可以继续优化空间。
-
由于动态规划中,我们比较两个子串,只依赖于各减少最后一个字符的子串的编辑距离,所以我们的动态规划数组是可以重复利用的,不需要二维数组,只需要一维数组即可,即滚动数组的方式。
题解:
rust:
二维数组(易懂)
impl Solution {pub fn min_distance(word1: String, word2: String) -> i32 {let l1 = word1.len();let l2 = word2.len();// 有一个字符串为空串if l1 == 0 || l2 == 0 {return (l1 + l2) as i32;}// DP 数组let mut dp = vec![vec![0; l2 + 1]; l1 + 1];// 边界状态初始化(0..=l1).for_each(|i| {dp[i][0] = i;});(0..=l2).for_each(|i| {dp[0][i] = i;});// 计算所有 DP 值(1..=l1).for_each(|i| {(1..=l2).for_each(|j| {let insert1 = dp[i - 1][j] + 1;let insert2 = dp[i][j - 1] + 1;let replace1 = if word1.as_bytes()[i - 1] != word2.as_bytes()[j - 1] {dp[i - 1][j - 1] + 1} else {// 两个字母相同,不用修改,所以操作次数不变dp[i - 1][j - 1]};dp[i][j] = insert1.min(insert2).min(replace1);});});return dp[l1][l2] as i32;}
}
滚动数组(更加优化的内存空间)
impl Solution {pub fn min_distance(mut word1: String, mut word2: String) -> i32 {let mut l1 = word1.len();let mut l2 = word2.len();// 有一个字符串为空串if l1 == 0 {return l2 as i32;}if l2 == 0 {return l1 as i32;}// 让内层单词较短,可以让dp数组较小if l1 < l2 {let wt = word1;word1 = word2;word2 = wt;let lt = l1;l1 = l2;l2 = lt;}// DP 滚动数组let mut dp = (0..=l2).collect::<Vec<_>>();// 计算所有 DP 值word1.bytes().enumerate().for_each(|(i1, c1)| {let mut pre = i1;dp[0] = pre + 1;word2.bytes().enumerate().for_each(|(i2, c2)| {let tmp = dp[i2 + 1];if c1 == c2 {dp[i2 + 1] = pre;} else {// dp[i2 + 1]:相当于向第一个单词插入一个字母// dp[i2]:相当于向第二个单词插入一个字母// pre: 相当于修改第一个单词一个字母dp[i2 + 1] = dp[i2 + 1].min(dp[i2]).min(pre) + 1;}pre = tmp;});});dp[l2] as i32}
}
go:
func minDistance(word1 string, word2 string) int {l1 := len(word1)l2 := len(word2)// 有一个字符串为空串if l1 == 0 {return l2}if l2 == 0 {return l1}// 让内层单词较短,可以让dp数组较小if l1 < l2 {word1, word2 = word2, word1l1, l2 = l2, l1}// DP 滚动数组dp := make([]int, l2+1)for i := 1; i <= l2; i++ {dp[i] = i}// 计算所有 DP 值for i1, c1 := range word1 {pre := i1dp[0] = pre + 1for i2, c2 := range word2 {tmp := dp[i2+1]if c1 == c2 {dp[i2+1] = pre} else {// dp[i2 + 1]:相当于向第一个单词插入一个字母// dp[i2]:相当于向第二个单词插入一个字母// pre: 相当于修改第一个单词一个字母if dp[i2+1] > dp[i2] {dp[i2+1] = dp[i2]}if dp[i2+1] > pre {dp[i2+1] = pre}dp[i2+1] += 1}pre = tmp}}return dp[l2]
}
c++:
class Solution {
public:int minDistance(string word1, string word2) {int l1 = word1.length(), l2 = word2.length();// 有一个字符串为空串if (l1 == 0) {return l2;}if (l2 == 0) {return l1;}// 让内层单词较短,可以让dp数组较小if (l1 < l2) {string wt = word1;word1 = word2;word2 = wt;int lt = l1;l1 = l2;l2 = lt;}// DP 滚动数组int dp[l2 + 1];for (int i = 1; i <= l2; ++i) {dp[i] = i;}// 计算所有 DP 值for (int i1 = 0; i1 < l1; ++i1) {int pre = i1;dp[0] = pre + 1;for (int i2 = 0; i2 < l2; ++i2) {const int tmp = dp[i2 + 1];if (word1[i1] == word2[i2]) {dp[i2 + 1] = pre;} else {// dp[i2 + 1]:相当于向第一个单词插入一个字母// dp[i2]:相当于向第二个单词插入一个字母// pre: 相当于修改第一个单词一个字母dp[i2 + 1] = min(min(dp[i2 + 1], dp[i2]), pre) + 1;}pre = tmp;}}return dp[l2];}
};
python:
class Solution:def minDistance(self, word1: str, word2: str) -> int:l1 = len(word1)l2 = len(word2)# 有一个字符串为空串if l1 == 0:return l2if l2 == 0:return l1# 让内层单词较短,可以让dp数组较小if l1 < l2:word1, word2 = word2, word1l1, l2 = l2, l1# DP 数组dp = [x for x in range(l2 + 1)]# 计算所有 DP 值for i1 in range(l1):pre = i1dp[0] = pre + 1for i2 in range(l2):tmp = dp[i2 + 1]if word1[i1] == word2[i2]:dp[i2 + 1] = preelse:# dp[i2 + 1]:相当于向第一个单词插入一个字母# dp[i2]:相当于向第二个单词插入一个字母# pre: 相当于修改第一个单词一个字母dp[i2 + 1] = min(dp[i2 + 1], dp[i2], pre) + 1pre = tmpreturn dp[l2]java:
class Solution {public int minDistance(String word1, String word2) {int l1 = word1.length(), l2 = word2.length();// 有一个字符串为空串if (l1 == 0) {return l2;}if (l2 == 0) {return l1;}// 让内层单词较短,可以让dp数组较小if (l1 < l2) {String wt = word1;word1 = word2;word2 = wt;int lt = l1;l1 = l2;l2 = lt;}// DP 滚动数组int[] dp = new int[l2 + 1];for (int i = 1; i <= l2; ++i) {dp[i] = i;}// 计算所有 DP 值for (int i1 = 0; i1 < l1; ++i1) {int pre = i1;dp[0] = pre + 1;for (int i2 = 0; i2 < l2; ++i2) {final int tmp = dp[i2 + 1];if (word1.charAt(i1) == word2.charAt(i2)) {dp[i2 + 1] = pre;} else {// dp[i2 + 1]:相当于向第一个单词插入一个字母// dp[i2]:相当于向第二个单词插入一个字母// pre: 相当于修改第一个单词一个字母dp[i2 + 1] = Math.min(Math.min(dp[i2 + 1], dp[i2]), pre) + 1;}pre = tmp;}}return dp[l2];}
}
非常感谢你阅读本文~
欢迎【点赞】【收藏】【评论】三连走一波~
放弃不难,但坚持一定很酷~
希望我们大家都能每天进步一点点~
本文由 二当家的白帽子:https://le-yi.blog.csdn.net/ 博客原创~
相关文章:

算法leetcode|72. 编辑距离(rust重拳出击)
文章目录 72. 编辑距离:样例 1:样例 2:提示: 分析:题解:rust:二维数组(易懂)滚动数组(更加优化的内存空间) go:c:python&a…...

实训笔记8.21
8.21笔记 8.21笔记一、Hive数据仓库技术的基本概念和组成1.1 Hive的组成架构1.1.1 Hive的客户端(1)Hive的命令行客户端 hive命令(2)Hive的JDBC的客户端(Java API)hive的JDBC客户端又有多种使用方式 &#x…...

robust distortion-free watermarks for language models
本文是LLM系列文章,针对《robust distortion-free watermarks for language models》的翻译。 语言模的鲁棒无失真水印 摘要1 引言2 方法和理论分析3 实验结果4 讨论 摘要 我们提出了一种从自回归语言模型中在文本中植入水印的方法,该方法对扰动具有鲁…...
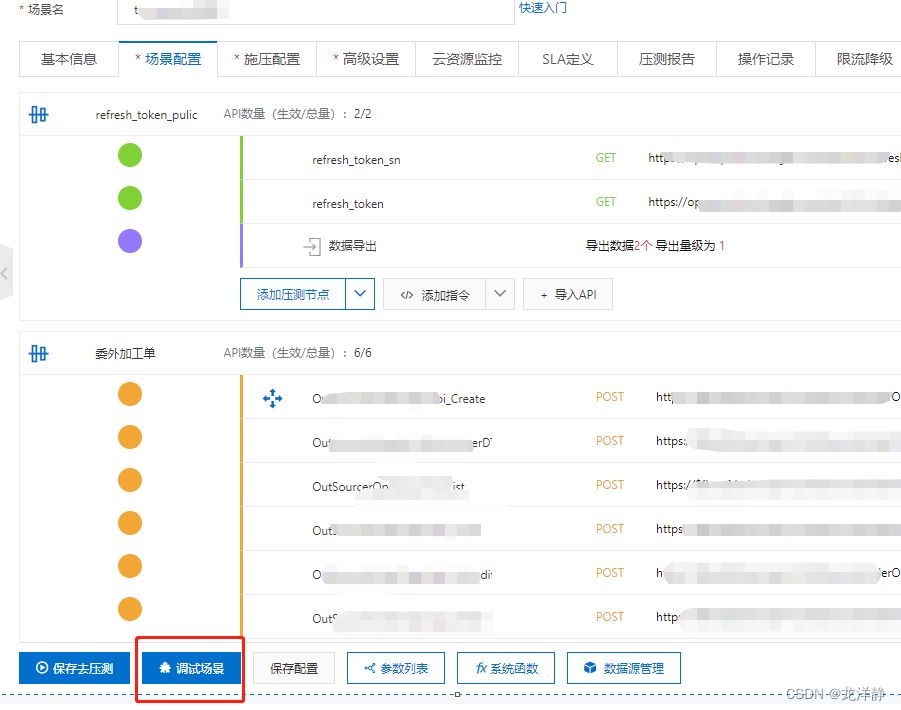
PTS性能测试工具-使用记录
因为PTS使用是要收费的,所以文中会有大量图片记录,为我自己以后工作中,可能会再次使用PTS做个参照,以免时间长,容易忘记~ 目录 一、创建场景 二、填写一个压测节点 1、填写节点基本信息 2、Body / Header填写 …...
【boost网络库从青铜到王者】第六篇:asio网络编程中的socket异步读(接收)写(发送)
文章目录 1、简介2、异步写 void AsyncWriteSomeToSocketErr(const std::string& buffer)3、异步写void AsyncWriteSomeToSocket(const std::string& buffer)4、异步写void AsyncSendToSocket(const std::string& buffer)5、异步读void AsyncReadSomeToSocket(cons…...

django sqlite3操作和manage.py功能介绍
参考链接:https://www.cnblogs.com/csd97/p/8432715.html manage.py 常用命令_python manage.py_追逐&梦想的博客-CSDN博客 python django操作sqlite3_django sqlite_浪子仙迹的博客-CSDN博客...

【SQL语句】SQL编写规范
简介 本文编写原因主要来于XC迁移过程中修改SQL语句时,发现大部分修改均源自于项目SQL编写不规范,以此文档做以总结。 注:此文档覆盖不甚全面,大体只围绕迁移遇到的修改而展开。 正文 1、【字段引号】 列名、表名如无特殊情况…...
)
后端项目开发:工具类封装(序列化、反射)
1.整合Jackson 根据《阿里巴巴开发规范》,包名使用单数,类名可以使用复数。 所以generic-common创建util包和utils工具类 很多时候我们需要将接收到的json数据转换为对象,或者将对象转为json存储。这时候我们需要编写用于json转换的工具类。…...

软件测试技术分享丨遇到bug怎么分析?
为什么定位问题如此重要? 可以明确一个问题是不是真的“bug” 很多时候,我们找到了问题的原因,结果发现这根本不是bug。原因明确,误报就会降低 多个系统交互,可以明确指出是哪个系统的缺陷,防止“踢皮球…...

LeetCode无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 输入: s “abcabcbb” 输出: 3 解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。 示例 2: 输入: s “bbbbb” 输出: 1 解释: 因为无重复字符的最长子串是 “…...

17.2.2 【Linux】通过systemctl观察系统上所有的服务
使用 systemctl list-unit-files 会将系统上所有的服务通通列出来~而不像 list-units 仅以 unit 分类作大致的说明。 至于 STATE 状态就是前两个小节谈到的开机是否会载入的那个状态项目。主要有 enabled / disabled / mask / static 等等。 假设我不想要知道这么多…...

Redis扩容机制与一致性哈希算法解析
在分布式系统设计中,Redis是一个备受欢迎的内存数据库,而一致性哈希算法则是分布式系统中常用的数据分片和负载均衡技术。本文将深入探讨Redis的扩容机制以及一致性哈希算法的原理,同时提供示例代码以帮助读者更好地理解这两个重要概念。 推…...
BDA初级分析——可视化基础
一、可视化的作用 数据可视化——利用各种图形方式更加直观地呈现数据的过程 可视化的作用 1、更快地理解数据,找出数据的规律和异常 2、讲出数据背后的故事,辅助做出业务决策 3、给非专业人士提供数据探索的能力 数据分析问题如何通过可视化呈现&am…...
边缘计算节点BEC典型实践:如何快速上手PC-Farm服务器?
百度智能云边缘计算节点BEC(Baidu Edge Computing)基于运营商边缘节点和网络构建,一站式提供靠近终端用户的弹性计算资源。边缘计算节点在海外覆盖五大洲,在国内覆盖全国七大区、三大运营商。BEC通过就近计算和处理,大…...

python自动把内容发表到wordpress完整示例及错误解答
要实现 Python 自动将内容发布到 WordPress,可以使用 Python 的 wordpress_xmlrpc 库,该库提供了使用 WordPress XML-RPC API 进行内容发布和管理的功能。 需要安装一下第三方库:wordpress_xmlrpc! pip install python_wordpress_xmlrpc 下面是一个简单的示例代码,可以实…...
【javaweb】学习日记Day6 - Mysql 数据库 DDL DML DQL
之前学习过的SQL语句笔记总结戳这里→【数据库原理与应用 - 第六章】T-SQL 在SQL Server的使用_Roye_ack的博客-CSDN博客 目录 一、概述 1、如何安装及配置路径Mysql? 2、SQL分类 二、DDL 数据定义 1、数据库操作 2、IDEA内置数据库使用 (1&…...

如何利用SFTP如何实现更安全的远程文件传输 ——【内网穿透】
🎬 鸽芷咕:个人主页 🔥 个人专栏: 《高效编程技巧》《cpolar》 ⛺️生活的理想,就是为了理想的生活! 文章目录 1. 安装openSSH1.1 安装SSH1.2 启动ssh 2. 安装cpolar2.1 配置termux服务 3. 远程SFTP连接配置3.1 查看生成的随机公…...

枚举和反射
枚举 枚举 枚举是一种特殊的类,它可以有自己的属性、方法和构造方法。 两种枚举的方法 自定义枚举 a.将构造器私有化,防止外部直接new b.去掉set方法,防止属性被修改 c.在内部直接创建固定的对象 通过类名直接去访问 关键字枚举 用…...

MinIO【部署 01】MinIO安装及SpringBoot集成简单测试
MinIO安装及SpringBoot集成测试 1.下载安装1.1 Install the MinIO Server1.2 Launch the MinIO Server1.3 Connect Your Browser to the MinIO Server 2.SpringBoot集成2.1 依赖及配置2.2 代码2.3 测试结果 1.下载安装 下载 https://min.io/download#/linux; 安装文…...

问道管理:证券代码是什么?有什么用?
交流炒股经历时,有些股民一时忘了股票发行公司的全称,会直接报一串数字来代替,这串数字的内容是证券代码,那么,证券代码是什么?它又起什么作用?关于这些,为大家准备了以下参考内容。…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
