To_Heart—题解——P6234 [eJOI2019] T形覆盖
link.
突然很想写这篇题解。虽然题目不算难。
考场只有30分是为什么呢?看来是我没有完全理解这道题目吧!
首先很明显的转换是,把 T 型覆盖看成十字形,再考虑最后减去某一块的贡献。
然后然后直接往原图上面放十字形!对于每一个十字的中心来说,实际上它只需要三个相邻的方块就可以了。而我们发现两个十字重合的部分不会超过两个方块,也就是说把这两个方块任意分配给两个人,就能保证这两个每个人都只会舍弃一个方块。
因为每次两个十字的重合最多只能让每个点丢弃一个方块,并且每次重合至少有一个十字会丢弃掉一个方块,所以惊天的结论是我们可以直接计算整个十字连通块的中心点和非中心点的个数。如果非中心点的个数大于等于中心点的个数的三倍,那么当前连通块一定合法,否则不能保证每个十字的中心点都能分配到刚好三个非中心点,即无解。
但是可能有非中心点的个数大于中心点的个数的三倍。这种情况说明所有的十字都只重合了一个点,那么必须要丢掉一个非中心点。因为要权值最大所以丢掉最小权值的就好了。
其实这个的实现方式有很多,但是我使用了并查集。为什么呢?因为其他题解就是用的并查集啊!
然后并查集需要注意的点就是不能选择中心点啊。中心点的权值设为最大值好不好。
#include<bits/stdc++.h>
using namespace std;int n,m,k;
int a[1000005];
int ID(int x,int y){return (x-1)*m+y;
}
int pre[1000005],dp[1000005];
int sz[1000005][2];
long long sum[1000005];bool vis[1000005];struct zz{int x,y;
}t[1000005];int Find(int x){if(pre[x]!=x) pre[x]=Find(pre[x]);return pre[x];
}
void Join(int x,int y){int fx=Find(x),fy=Find(y);if(fx==fy) return ;pre[fy]=fx,sum[fx]+=sum[fy],dp[fx]=min(dp[fx],dp[fy]),sz[fx][0]+=sz[fy][0],sz[fx][1]+=sz[fy][1];
}int fx[5]={0,1,-1,0,0};
int fy[5]={0,0,0,1,-1};int main(){
// freopen("t-covering.in","r",stdin);
// freopen("t-covering.out","w",stdout);cin>>n>>m;for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%d",&a[ID(i,j)]);cin>>k;for(int i=1,x,y;i<=k;i++) scanf("%d%d",&x,&y),t[i]=(zz){x+1,y+1};for(int i=1;i<=k;i++) vis[ID(t[i].x,t[i].y)]=1;for(int i=1;i<=n*m;i++){pre[i]=i,sum[i]=a[i],dp[i]=a[i],sz[i][vis[i]]=1;if(vis[i]) dp[i]=0x3f3f3f3f; }for(int i=1;i<=k;i++) for(int j=1;j<=4;j++){int x=t[i].x,y=t[i].y;int dx=x+fx[j],dy=y+fy[j];if(dx<=0||dx>n||dy<=0||dy>m) continue;Join(ID(x,y),ID(dx,dy)); }long long ans=0;memset(vis,0,sizeof vis);for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){int x=(ID(i,j));int fx=Find(x);if(vis[fx]) continue; vis[fx]=1;if(sz[fx][0]<sz[fx][1]*3) return printf("No\n"),0;else if(sz[fx][0]==sz[fx][1]*3) ans+=sum[fx];else ans+=sum[fx]-dp[fx];}cout<<ans<<endl;return 0;
}
相关文章:

To_Heart—题解——P6234 [eJOI2019] T形覆盖
link. 突然很想写这篇题解。虽然题目不算难。 考场只有30分是为什么呢?看来是我没有完全理解这道题目吧! 首先很明显的转换是,把 T 型覆盖看成十字形,再考虑最后减去某一块的贡献。 然后然后直接往原图上面放十字形!对于每一个…...

[软件工具]精灵标注助手目标检测数据集格式转VOC或者yolo
有时候我们拿到一个数据集发现是xml文件格式如下: <?xml version"1.0" ?> <doc><path>C:\Users\Administrator\Desktop\test\000000000074.jpg</path><outputs><object><item><name>dog</name>…...
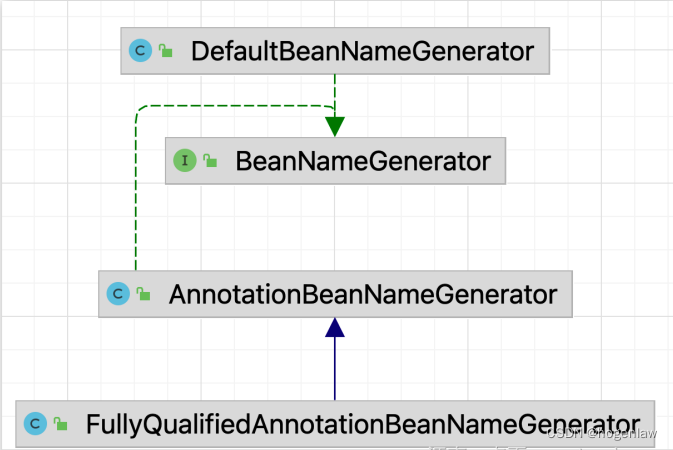
Spring BeanName自动生成原理
先看代码演示 项目先定义一个User类 public class User {private String name;Overridepublic String toString() {return "User{" "name" name \ };}public String getName() {return name;}public void setName(String name) {this.name name;} }…...
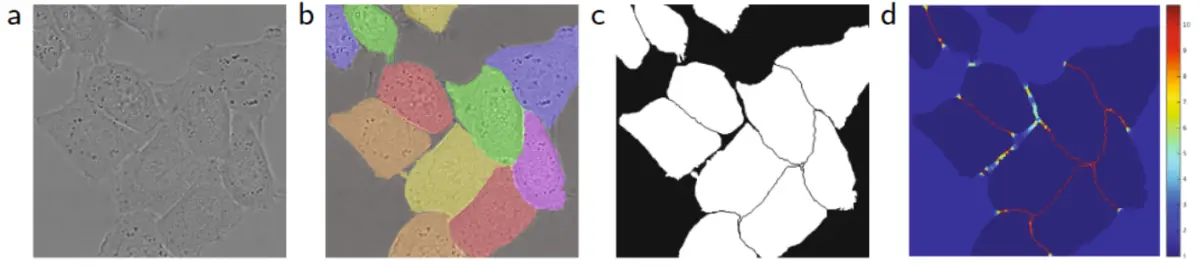
论文阅读_图形图像_U-NET
name_en: U-Net: Convolutional Networks for Biomedical Image Segmentation name_ch: U-Net:用于生物医学图像分割的卷积网络 addr: http://link.springer.com/10.1007/978-3-319-24574-4_28 doi: 10.1007/978-3-319-24574-4_28 date_read: 2023-02-08 date_publi…...

基于热交换算法优化的BP神经网络(预测应用) - 附代码
基于热交换算法优化的BP神经网络(预测应用) - 附代码 文章目录 基于热交换算法优化的BP神经网络(预测应用) - 附代码1.数据介绍2.热交换优化BP神经网络2.1 BP神经网络参数设置2.2 热交换算法应用 4.测试结果:5.Matlab代…...

基于秃鹰算法优化的BP神经网络(预测应用) - 附代码
基于秃鹰算法优化的BP神经网络(预测应用) - 附代码 文章目录 基于秃鹰算法优化的BP神经网络(预测应用) - 附代码1.数据介绍2.秃鹰优化BP神经网络2.1 BP神经网络参数设置2.2 秃鹰算法应用 4.测试结果:5.Matlab代码 摘要…...
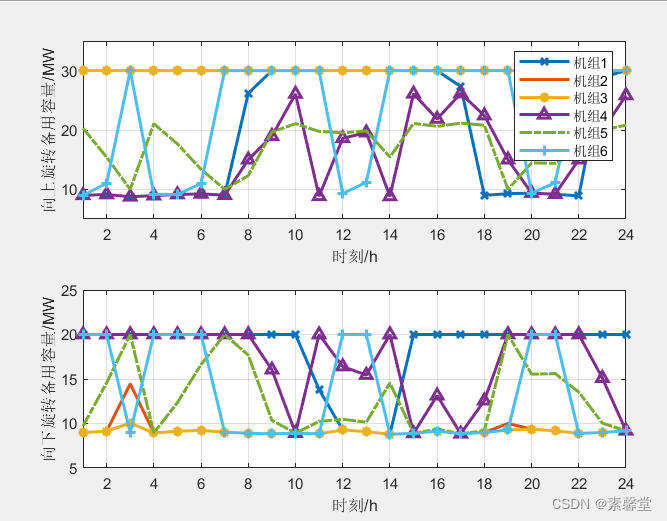
2.文章复现《热电联产系统在区域综合能源系统中的定容选址研究》(附matlab程序)
0.代码链接 1.简述 光热发电是大规模利用太阳能的新兴方式,其储热系 统能够调节光热电站的出力特性,进而缓解光热电站并网带来的火电机组调峰问题。合理配置光热电站储热容量,能够 有效降低火电机组调峰成本。该文提出一种光热电站储热容 量配…...
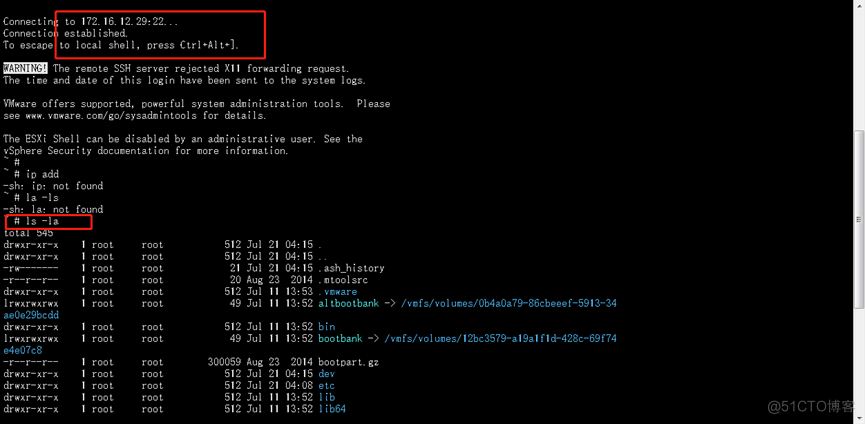
如何开启esxi主机的ssh远程连接
环境:esxi主机,说明:esxi主机默认ssh是不开启的,需要人工手动启动,也可以设置同esxi主机一起开机启动。 1、找到esxi主机,点击“配置”那里,再点击右边的属性,如图所示: …...

Android Studio实现解析HTML获取json,解析json图片URL,将URL存到list,进行瀑布流展示
目录 效果build.gradle(app)添加的依赖(用不上的可以不加)AndroidManifest.xml错误activity_main.xmlitem_image.xmlMainActivityImage适配器ImageModel 接收图片URL 效果 build.gradle(app)添加的依赖&…...

Centos7 交叉编译QT5.9.9源码 AArch64架构
环境准备 centos7 镜像 下载地址:http://mirrors.aliyun.com/centos/7.9.2009/isos/x86_64/ aarch64交叉编译链 下载地址:https://releases.linaro.org/components/toolchain/binaries/7.3-2018.05/aarch64-linux-gnu/ QT5.9.9源代码 下载地址࿱…...
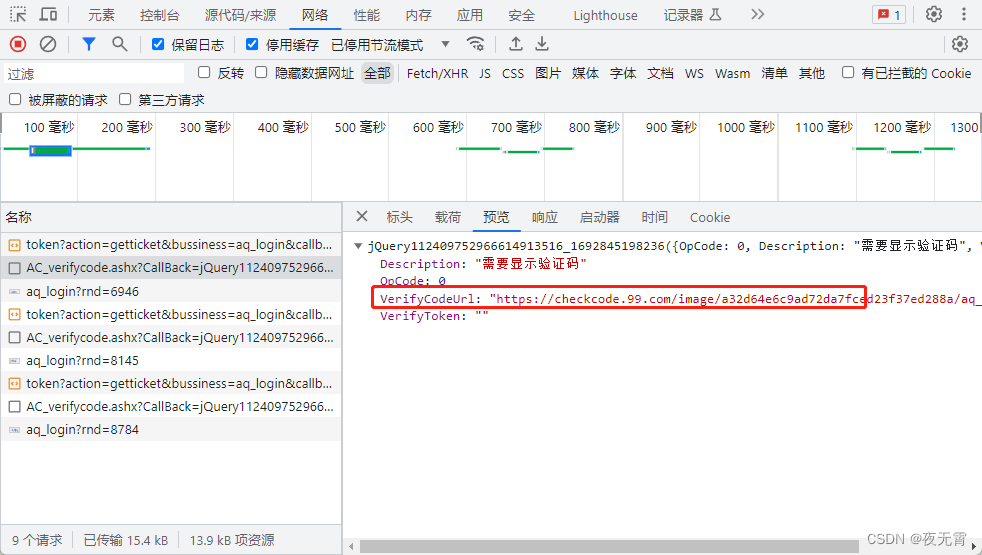
爬虫逆向实战(二十)--某99网站登录
一、数据接口分析 主页地址:某99网站 1、抓包 通过抓包可以发现登录接口是AC_userlogin 2、判断是否有加密参数 请求参数是否加密? 通过查看“载荷”可以发现txtPassword和aws是加密参数 请求头是否加密? 无响应是否加密? 无…...

【C# 基础精讲】LINQ to Objects查询
LINQ to Objects是LINQ技术在C#中的一种应用,它专门用于对内存中的对象集合进行查询和操作。通过使用LINQ to Objects,您可以使用统一的语法来查询、过滤、排序、分组等操作各种.NET对象。本文将详细介绍LINQ to Objects的基本概念、常见的操作和示例&am…...

【力扣】209. 长度最小的子数组 <滑动窗口>
【力扣】209. 长度最小的子数组 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其和 ≥ target 的长度最小的连续子数组 [numsl, numsl1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。 示例 1&a…...

帮助中心应该用什么工具做?
在线帮助中心是指一个位于互联网上的资源平台,提供给用户获取产品或服务相关信息、解决问题以及获取技术支持的渠道。它通常包含了组织化的知识库、常见问题解答(FAQ)、操作指南、教程视频、用户手册等内容。在线帮助中心的主要目标是为用户提…...

前端面试:【跨域与安全】跨域问题及解决方案
嗨,亲爱的Web开发者!在构建现代Web应用时,跨域问题和安全性一直是不可忽视的挑战之一。本文将深入探讨跨域问题的背景以及解决方案,以确保你的应用既安全又能与其他域名的资源进行互操作。 1. 什么是跨域问题? 跨域问…...
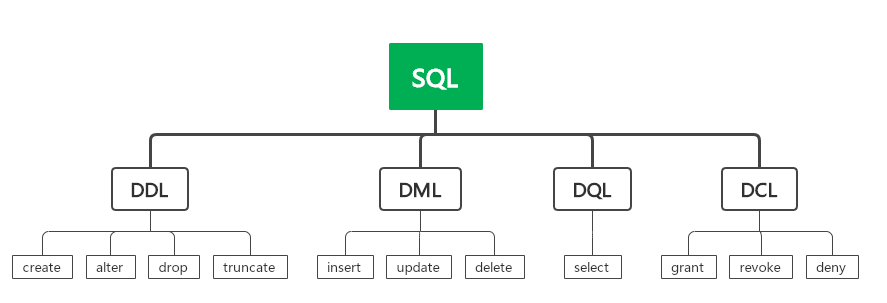
【SQL中DDL DML DQL DCL所包含的命令】
SQL中DDL DML DQL DCL所包含的命令 关于DDL、DML、DQL、DCL的定义和适用范围如下: 数据定义语言(Data Definition Language,DDL): DDL用于创建、修改和删除数据库中的表、视图、索引等对象。它的主要命令包括CREATE、A…...
LeetCode150道面试经典题-- 二叉树的最大深度(简单)
1.题目 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 2.示例 3.思路 深度优先遍历 一个二叉树要查询到最大深度,可以将问题转为从根节点出发,查看左右子树的最大深度&am…...
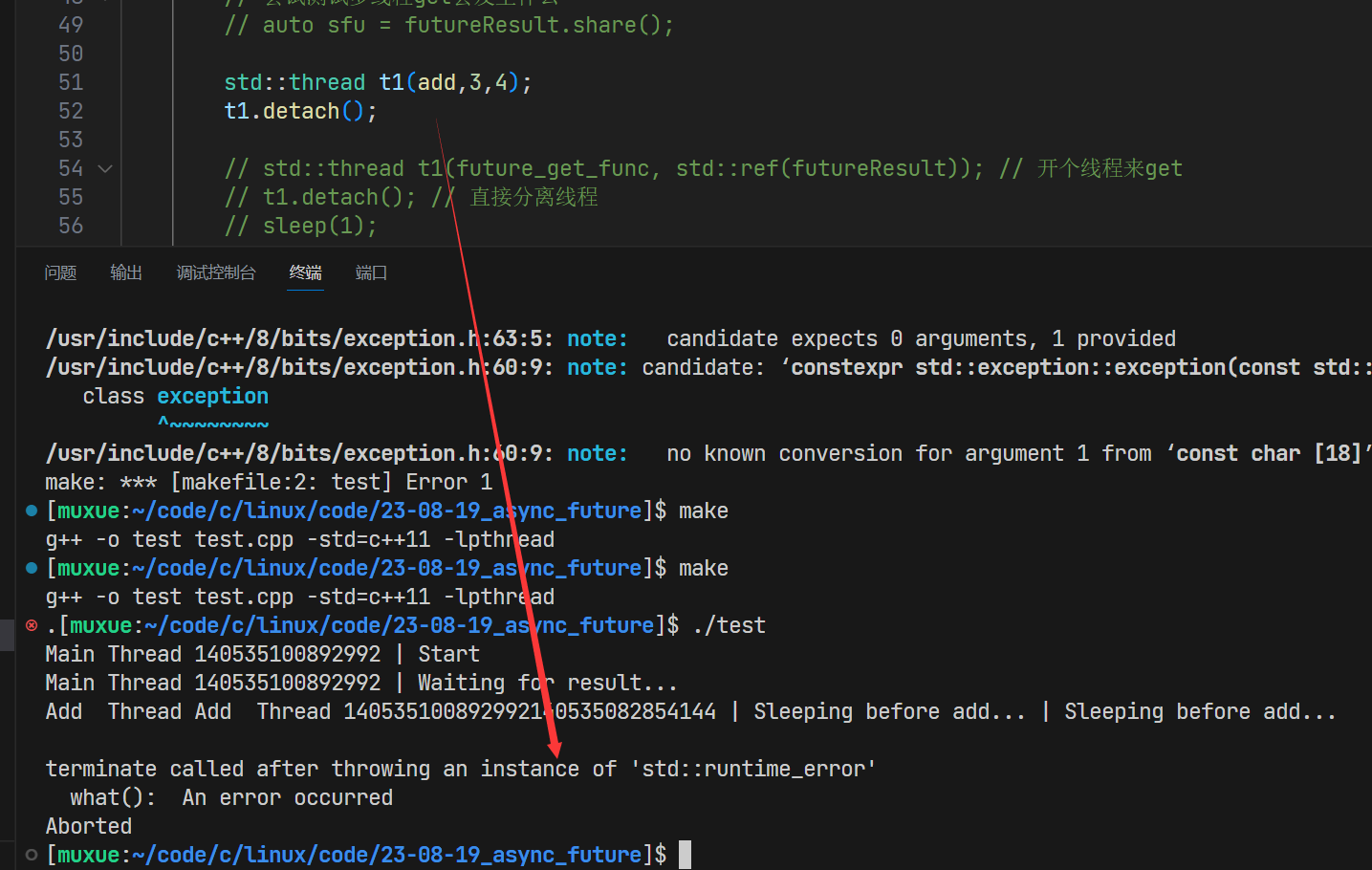
【C++11】future和async等
C11的future和async等关键字 1.async和future的概念 std::async 和 std::future 是 C11 引入的标准库功能,用于实现异步编程,使得在多线程环境中更容易处理并行任务。它们可以帮助你在不同线程中执行函数,并且能够方便地获取函数的结果。 在…...
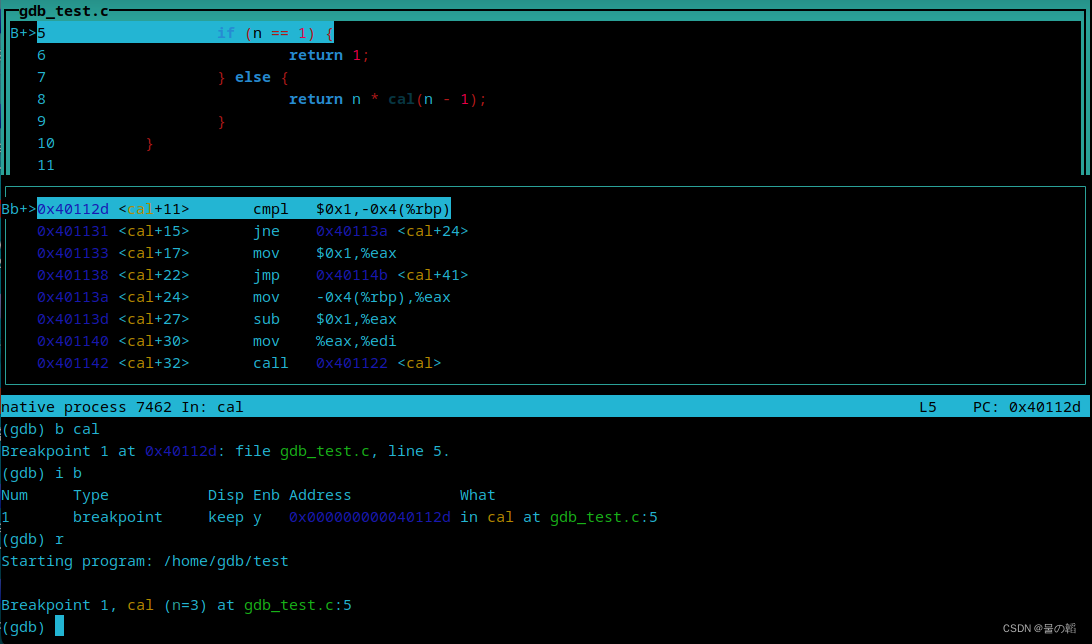
Linux 系统下 GDB 调试器的使用
文章目录 简介GDB 的介绍GDB 的使用 GDB 常用命令及示例查看相关操作断点相关操作运行相关操作变量相关操作分隔窗口操作 简介 GDB 的介绍 GDB 是 GNU 调试程序,是用来调试 C 和 C 程序的调试器。它可以让程序开发者在程序运行时观察程序的内部结构和内存的使用情况…...

个人首次使用UniAPP使用注意事项以及踩坑
个人首次使用UniAPP 使用注意事项以及踩坑 自我记录 持续更新 1.vscode 插件 uni-create-view 快速nui-app页面的 uni-helper uni-app代码提示的 uniapp小程序扩展 鼠标悬停查文档 Error Lens 行内提示报错 "types": ["dcloudio/types", "mini…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
