应知道的python基础知识
1、运算符
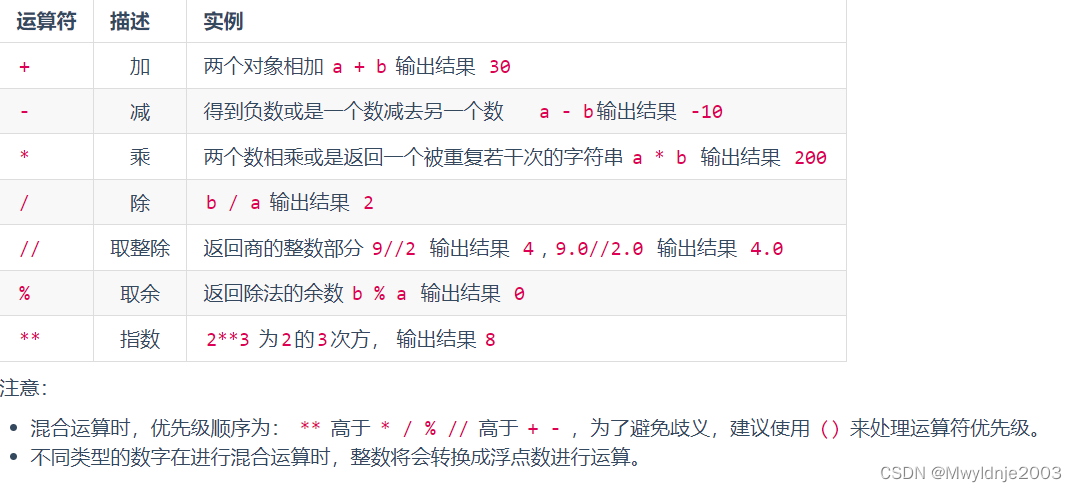
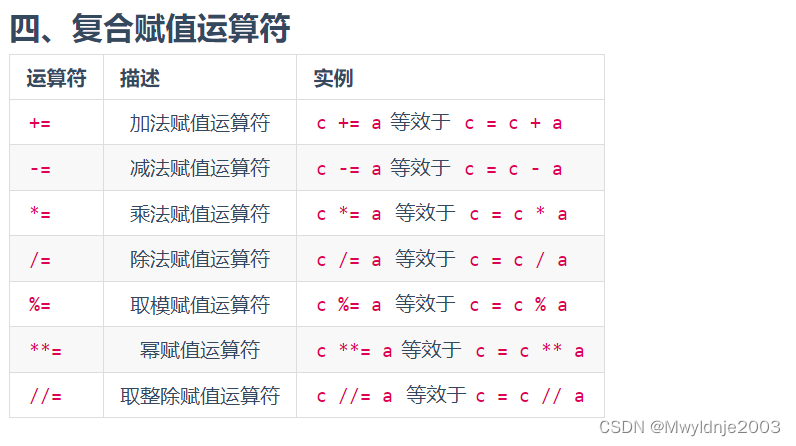
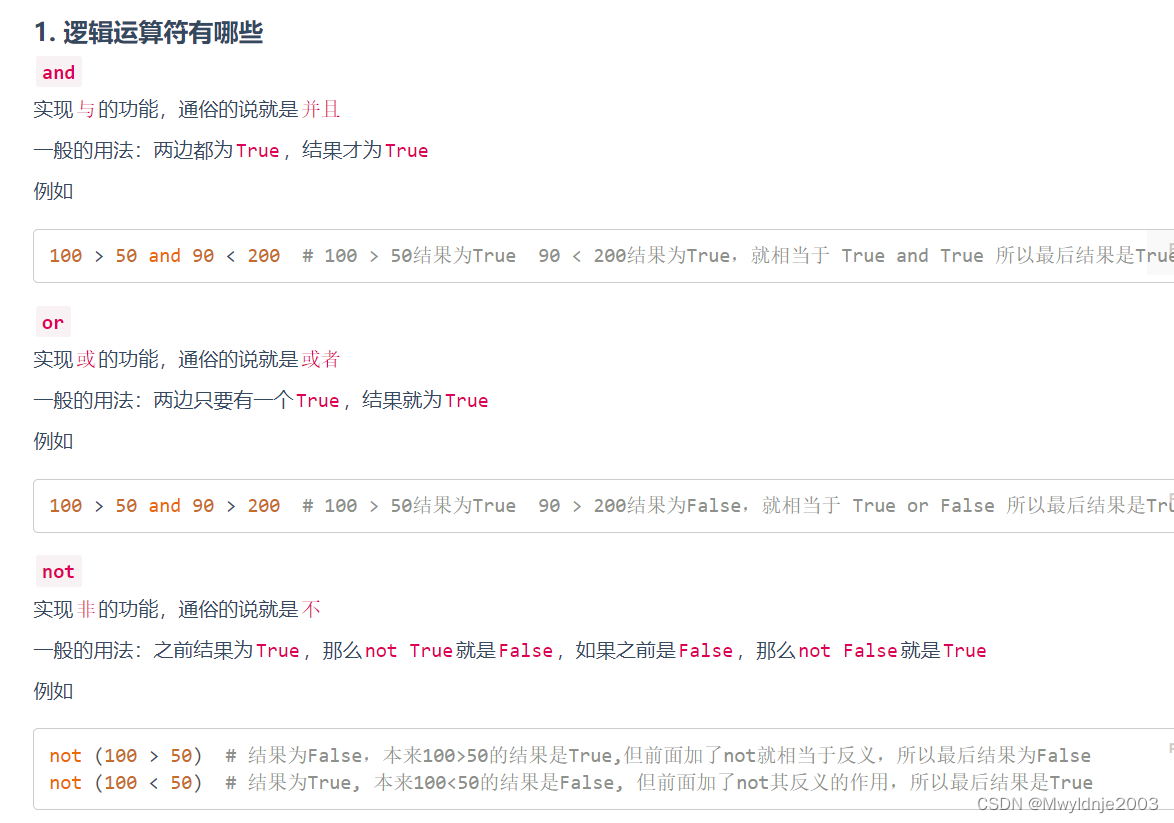
2、特殊情况下的逻辑运算
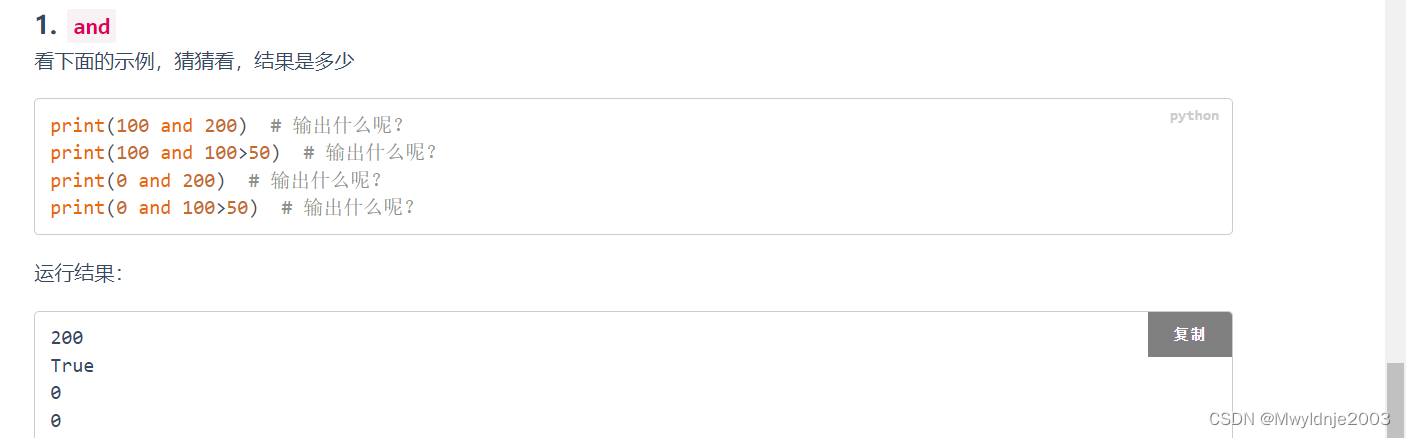


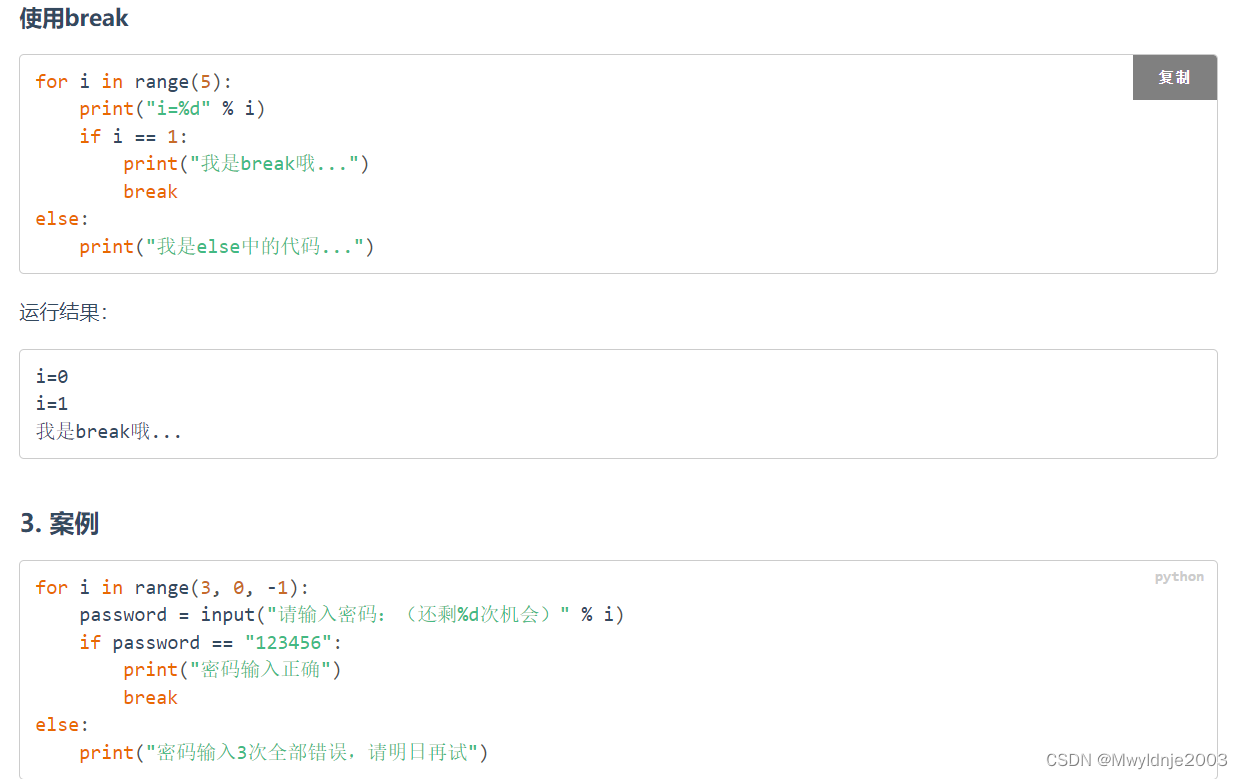
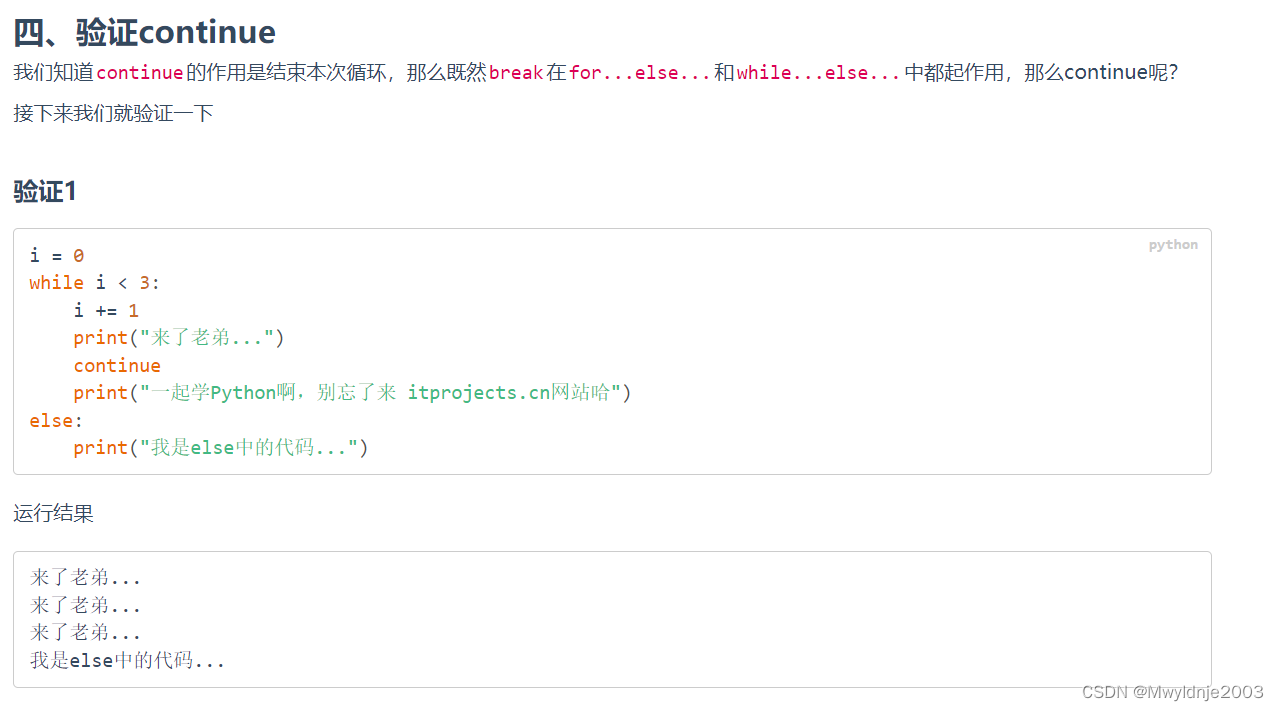
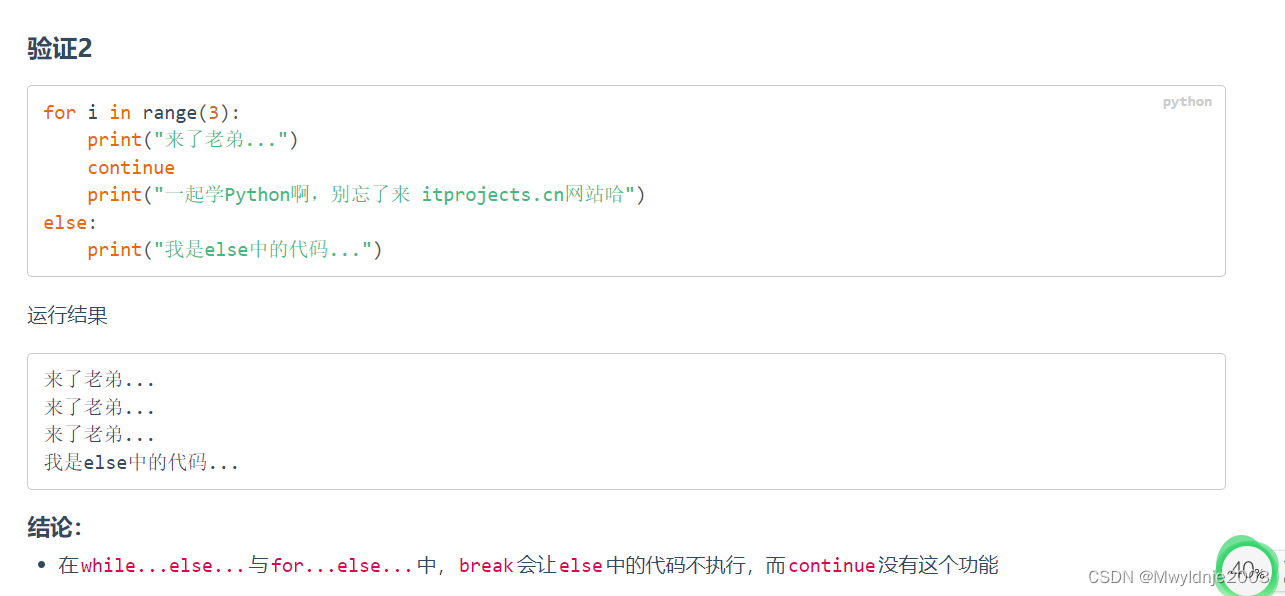
3、循环中的else
3.1 while else
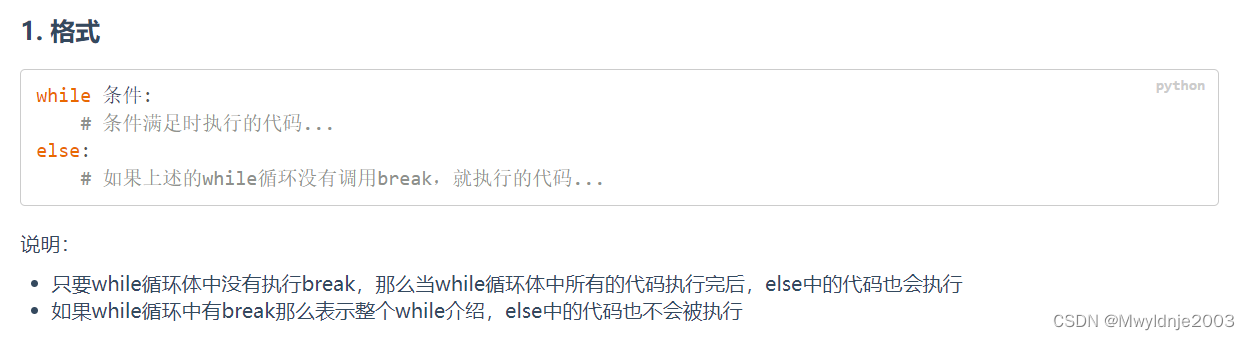
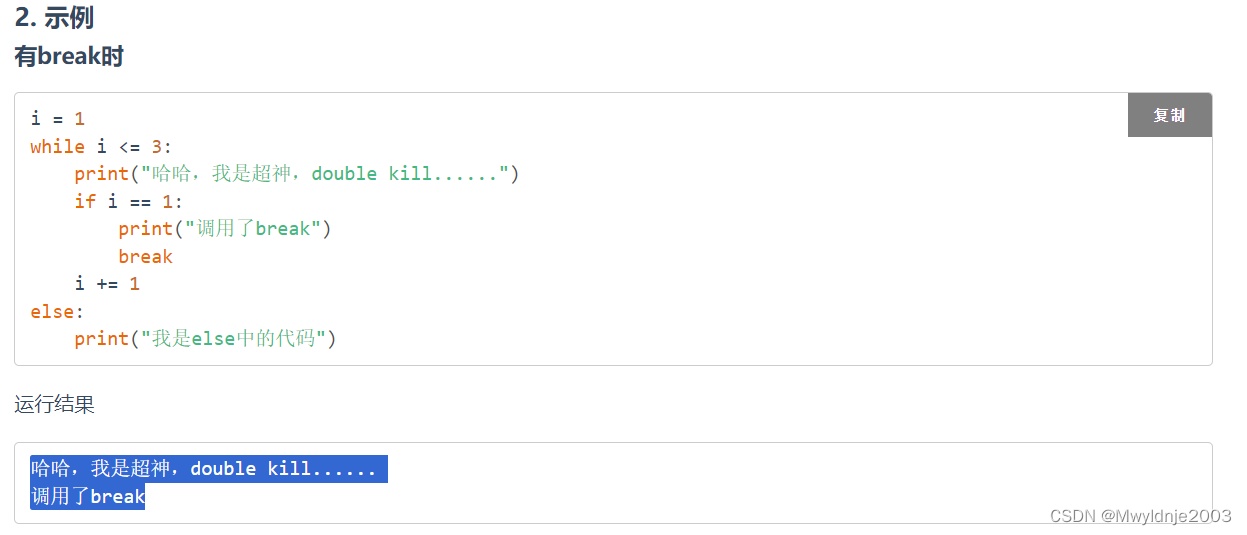
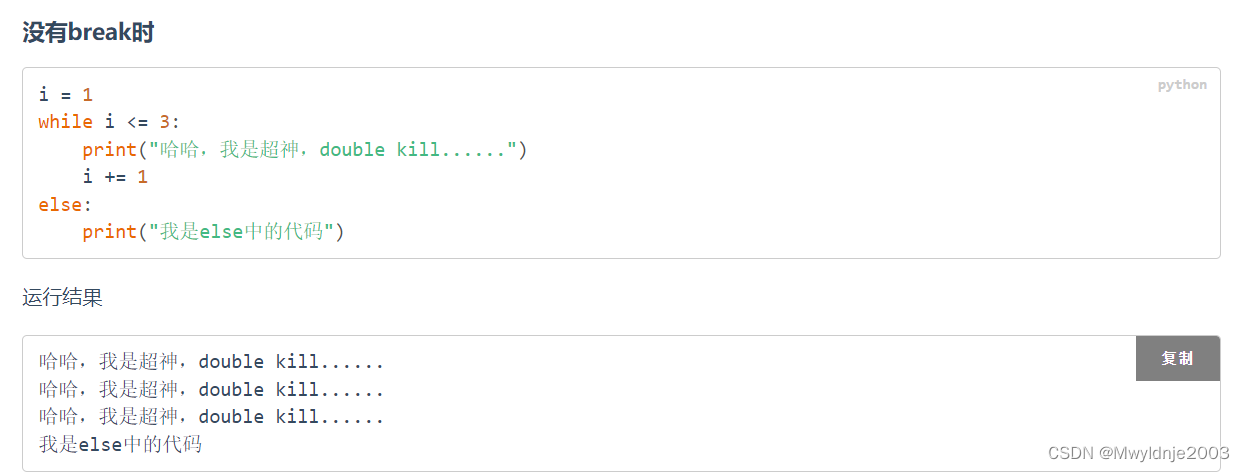
3.2 for else
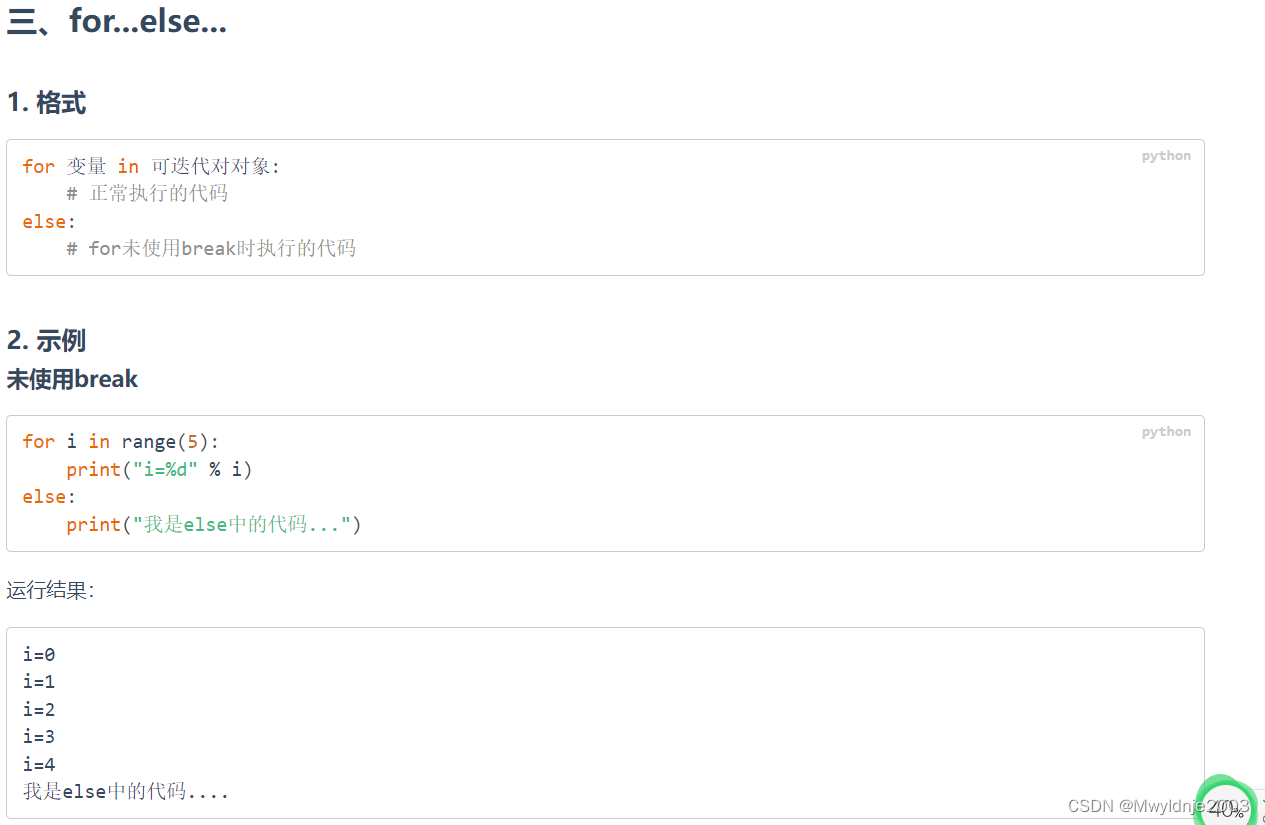
4、列表相关操作
列表的相关操作
4.1增(append, extend, insert)
- 通过append可以向列表添加元素:列表.append(新元素数据)
- 通过extend可以将另一个列表中的元素逐一添加到列表中:列表.extend(另外一个列表)
- 在指定位置index(索引,理解为下标即可)前插入元素object:列表.insert(index, object)
4.2改:
修改元素的时候,要通过下标来确定要修改的是哪个元素,然后才能进行修改:列表[下标] = 新数据
4.3查(in, not in, count)
in(存在),如果存在那么结果为true,否则为false:数据 in 列表
not in(不存在),如果不存在那么结果为true,否则false :数据 not in 列表
count 查个数:列表.count(“要查询的数据”) # 结果就是找到的数据的个数
4.4删(del, pop, remove)
del:根据下标进行删除:del 列表[下表】
pop:删除最后一个元素:列表.pop()
remove:根据元素的值进行删除: 列表.remove(“值”)
4.5排序(sort, reverse)
sort:sort方法是将列表按特定顺序重新排列,默认为由小到大,参数reverse=True可改为倒序,由大到小。
>>> a = [1, 4, 2, 3]
>>> a.sort()
>>> a
[1, 2, 3, 4]
>>> a.sort(reverse=True)
>>> a
[4, 3, 2, 1]
reverse方法是将列表倒叙
>>> a = [1, 4, 2, 3]
>>> a
[1, 4, 2, 3]
>>> a.reverse()
>>> a
[3, 2, 4, 1]
5、列表、元组、集合的相互转换
列表、元组在定义时的顺序是怎样的,那么顺序就是怎样的
而集合的实际存储顺序与定义的顺序没有什么关系,而是与一个特殊的算法有关(把数据进行了哈希,这个我们暂不做深入讨论,只需要知道集合的顺序不确定即可),因为没有顺序,所以不可以用下标方式获取值,可以用for循环
元组不可修改
集合不可重复
nums1 = [11, 22, 33] # 定义列表
nums2 = (44, 55, 66) # 定义元组
nums3 = {77, 88, 99} # 定义集合# 列表转换为元组、集合
print("-----------")
nums1_tuple = tuple(nums1)
print(type(nums1_tuple))
nums1_set = set(nums1)
相关文章:

应知道的python基础知识
1、运算符 2、特殊情况下的逻辑运算 3、循环中的else 3.1 while else 3.2 for else 4、列表相关操作 列表的相关操作 4.1增(append, extend, insert) 通过append可以向列表添加元素:列表.append(新元素数据)通过extend可以将另一个列表中的元素逐一添加到列表中:列表.exte…...
FFmpeg<第一篇>:环境配置
1、官网地址 http://ffmpeg.org/download.html2、linux下载ffmpeg 下载: wget https://ffmpeg.org/releases/ffmpeg-snapshot.tar.bz2解压: tar xvf ffmpeg-snapshot.tar.bz23、FFmpeg ./configure编译参数汇总 解压 ffmpeg-snapshot.tar.bz2 之后&…...

深度学习:Sigmoid函数与Sigmoid层区别
深度学习:Sigmoid函数与Sigmoid层 1. Sigmoid神经网络层 vs. Sigmoid激活函数 在深度学习和神经网络中,“Sigmoid” 是一个常见的术语,通常用来表示两个相关但不同的概念:Sigmoid激活函数和Sigmoid神经网络层。这两者在神经网络…...

❤ Ant Design Vue 2.28的使用
❤ Ant Design Vue 2.28 弹窗 //按钮 <a-button type"primary" click"showModal">Open Modal</a-button>//窗口 <a-modal v-model:visible"visible" title"Basic Modal" ok"handleOk"><p>Some con…...

R语言02-R语言中的向量
概念 在R语言中,向量(Vector)是最基本的数据结构之一,用于存储相同类型的多个元素。向量可以包含数值、字符、逻辑值等,但其中的所有元素必须具有相同的数据类型。向量可以通过c()函数创建,也可以通过其他…...

windows linux 都可执行的脚本 bat, shell 共存
核心, 执行一行解析一行 windows:执行的地方进行解析, 可以任意跳转执行; bash从上往下解析执行; 一行行解析发现语法错误; 差异: windows可以部分不解析; linux需要从上往下解析合法; 总结:linux, windows可以一上一下共存 # linux code# windows code 关键: 脚本解析的差…...
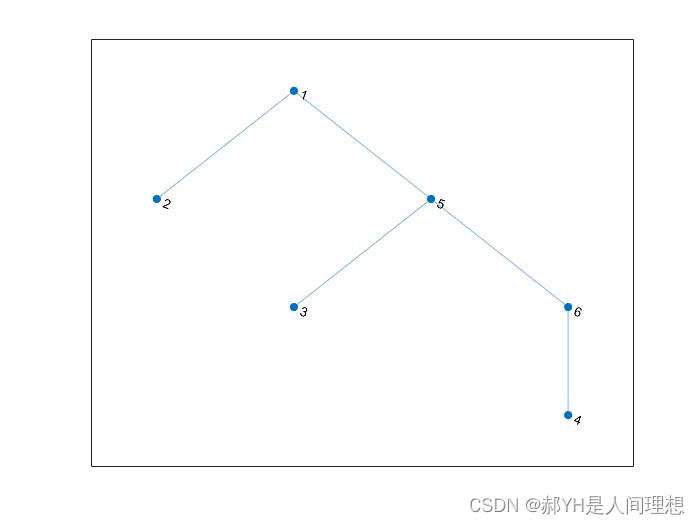
MATLAB图论合集(二)计算最小生成树
今天来介绍第二部分,图论中非常重要的知识点——最小生成树。作为数据结构的理论知识,Prim算法和克鲁斯卡尔算法的思想此处博主不详细介绍,建议在阅读本帖前熟练掌握。 对于无向带权图,在MATLAB中可以直接以邻接矩阵的方式创建出来…...
unity 模型显示在UI上 并交互(点击、旋转、缩放)
项目工程:unity模型显示在UI上并交互(点击、旋转、缩放)资源-CSDN文库 1.在Assets创建 Render Texture(下面会用到),根据需要设置Size 2.创建UIRawImage,并把Render Texture赋上 3.创建相机&am…...

html实现页面切换、顶部标签栏(可删、可切换,点击左侧超链接出现标签栏)
一、在一个页面(不跨页面) 效果: 代码 <!DOCTYPE html> <html><head><style>/* 设置标签页外层容器样式 */.tab-container {width: 100%;background-color: #f1f1f1;overflow: hidden;}/* 设置标签页选项卡的样式…...
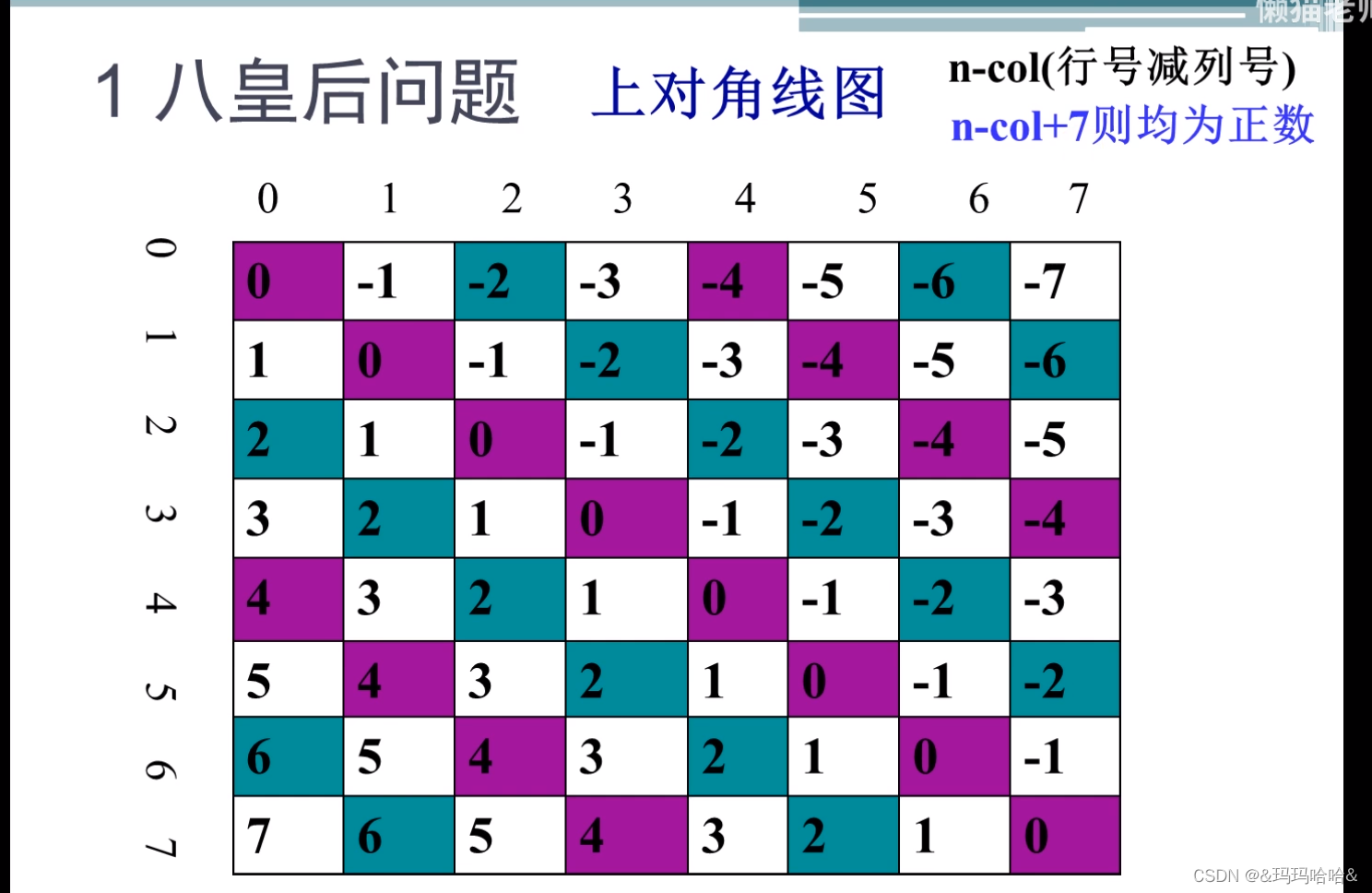
n-皇后问题(DFS)
n−皇后问题是指将 n 个皇后放在 nn 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。 现在给定整数 n,请你输出所有的满足条件的棋子摆法。 输入格式 共一行,包含整数 n。 输出…...

漏洞利用和权限提升
使用Kali Linux进行漏洞利用和权限提升是渗透测试过程中的一部分,用于评估系统的安全性。 漏洞利用: 选择目标: 首先,确定 要进行漏洞利用的目标系统。这可能是一个具有已知漏洞的应用程序、服务或操作系统。 收集信息ÿ…...

开源网安受邀参加软件供应链安全沙龙,推动企业提升安全治理能力
8月23日下午,合肥软件行业软件供应链安全沙龙在中安创谷科技园举办。此次沙龙由合肥软件产业公共服务中心联合中安创谷科技园公司共同主办,开源网安软件供应链安全专家王晓龙、尹杰受邀参会并带来软件供应链安全方面的精彩内容分享,共同探讨…...

回归分析扫盲:为什么非线性模型不能直接用最优子集选择法
最近有人给我发了篇文章: 一个问题有一堆变量,我们要选取哪些变量来建模呢?我们来看看这篇文章是怎么做的: 这个方法简单来说就是:对于这一堆变量,我们每次尝试剔除其中一个变量,然后用剩下的变…...

单例模式简介
概念: 单例模式(Singleton Pattern)是一种创建型设计模式,它确保一个类只有一个实例,并提供全局访问点。单例模式的核心思想是限制某个类只能创建一个对象实例,并提供对该实例的全局访问。这样可以避免多个…...
WPF自定义命令及属性改变处理
1、项目建构 2、自定义命令 namespace WpfDemo.Base {public class MyCommand : ICommand{Action executeAction;public MyCommand(Action action){executeAction action;}public event EventHandler? CanExecuteChanged;public bool CanExecute(object? parameter){retu…...

macbook m1 docker中使用go
已经有一个centos8的镜像,本来打算在centos8中安装go 安装方法: # 1.下载go的安装包 mkdir install && cd install # 任意创建个文件夹 wget https://go.dev/dl/go1.20.2.linux-amd64.tar.gz# 2. 解压 tar -C xzf go1.20.2.linux-amd64.tar.g…...
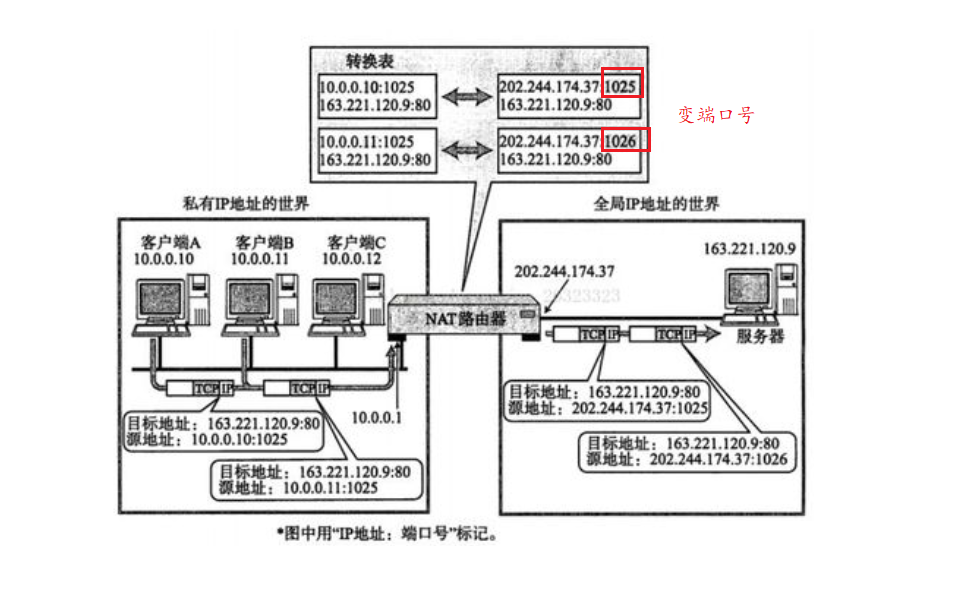
【Hello Network】DNS协议 NAT技术 代理服务器
本篇博客简介:介绍DNS协议 NAT技术和代理服务器 网络各协议补充 DNSDNS背景DNS介绍DNS总结域名简介 NAT技术NAT技术背景NAT IP转换过程NAPTNAT技术缺陷NAT和代理服务器 网络协议总结应用层传输层网络层数据链路层 DNS DNS是一整套从域名映射到IP的系统 DNS背景 为…...
Android 使用模拟器模拟Linux操作系统
1. 简介 在Android手机上使用模拟器模拟ubuntu等操作系统,便于测试 2. 软件准备 Termux:是一款 Android 终端模拟器和 Linux 环境应用程序,无需 root 或设置即可直接运行。虽然酷安和谷歌菜市场都能下载,但这些渠道都很久没更新…...

机器学习基础之《分类算法(5)—朴素贝叶斯算法原理》
一、朴素贝叶斯算法 1、什么是朴素贝叶斯分类方法 之前用KNN算法,分类完直接有个结果,但是朴素贝叶斯分完之后会出现一些概率值,比如: 这六个类别,它都有一定的可能性 再比如,对文章进行分类:…...

# Go学习-Day6
文章目录 Go学习-Day6封装继承接口 Go学习-Day6 个人博客:CSDN博客 封装 类似java的类的封装,这里我们利用大小写和工厂模式来实现封装的功能略过 继承 相似的类具有相似的方法,反复绑定相同的方法,代码冗余,所以引…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...
