深度学习优化入门:Momentum、RMSProp 和 Adam
目录
深度学习优化入门:Momentum、RMSProp 和 Adam
病态曲率
1牛顿法
2 Momentum:动量
3Adam
深度学习优化入门:Momentum、RMSProp 和 Adam

本文,我们讨论一个困扰神经网络训练的问题,病态曲率。
虽然局部极小值和鞍点会阻碍我们的训练,但病态曲率会减慢训练的速度,以至于从事机器学习的人可能会认为搜索已经收敛到一个次优的极小值。让我们深入了解什么是病态曲率。
「病态曲率」
考虑以下损失曲线图。

病态曲率
如你所知,我们在进入一个以蓝色为标志的像沟一样的区域之前是随机的。这些颜色实际上代表了在特定点上的损失函数的值,红色代表最高的值,蓝色代表最低的值。
我们想要下降到最低点,因此,需要穿过峡谷。这个区域就是所谓的病态曲率。为了了解为何将其称为病态曲率,让我们再深入研究。放大了看,病态曲率就像这样...

要知道这里发生的事情并不难。梯度下降沿着峡谷的山脊反弹,向最小的方向移动的速度非常慢。这是因为山脊的曲线在 W1 方向上弯曲的更陡。
考虑山脊表面的 A 点。我们看到,梯度在这点可以分解为两个分量,一个沿着 W1 方向,另外一个沿着 W2 方向。如果 f 显著下降的唯一方向是低曲率的,那么优化可能会变得太慢而不切实际,甚至看起来完全停止,造成局部最小值的假象。

正常情况下,我们使用一个较慢的学习率来解决这种山脊间反弹的问题,正如上一篇关于梯度下降的文章所述。然而,这却产生了麻烦。
当我们接近最小值时,慢下来是有意义的,我们想要收敛于它。但是考虑一下梯度下降进入病态曲率的区域,以及到最小值的绝对距离。如果我们使用较慢的学习率,可能需要花费更多的时间才能到达极小值点。事实上,有研究论文报道过使用足够小的学习率来阻值山脊间的反弹可能导致参与者以为损失根本没有改善,从而放弃训练。
如果 f 显著下降的唯一方向是低曲率的,那么优化可能会变得太慢而不切实际,甚至看起来完全停止,造成局部最小值的假象。
也许我们想要的是能让我们慢慢进入病态曲率底部的平坦区域,然后在最小值的方向上加速。二阶导数可以帮助我们做到这一点。
1牛顿法
梯度下降是一阶优化方法。它只考虑损失函数的一阶导数,而不考虑更高阶的导数。这基本上意味着它不知道损失函数的曲率。它只能说明损失是否下降以及下降的速度,而不能区分曲线是平坦的,向上的,还是向下的。

之所以会发生这种现象,是因为梯度下降只关心梯度,就好像上图中红色的点,三个曲线在这一点上的梯度是相同的。如何解决?使用二阶导数,或者考虑梯度变化的速率。
一个非常流行的可以使用二阶导数的技术,可以解决我们的问题,这个方法称为牛顿法。 如果表面变得不那么陡峭,那么学习步骤就会减少。
牛顿法可以提供一个理想的步长,在梯度方向上移动。由于我们现在有了关于损失表面曲率的信息,所以可以选择步长,而不是用病态曲率来超过该区域的极限。
牛顿法通过计算 Hessian 矩阵来实现,Hessian 矩阵是损失函数的二阶导数组成的权值组合。我所说的权值组合,如下所示。
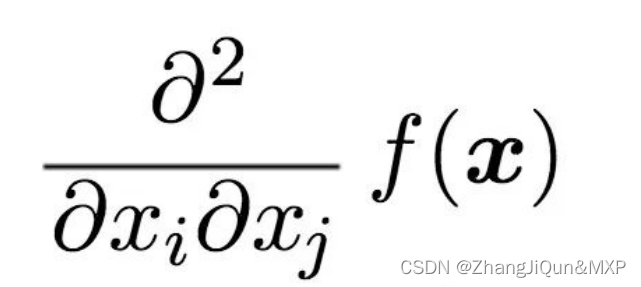
Hessian 矩阵在一个大矩阵中计算所有这些梯度。
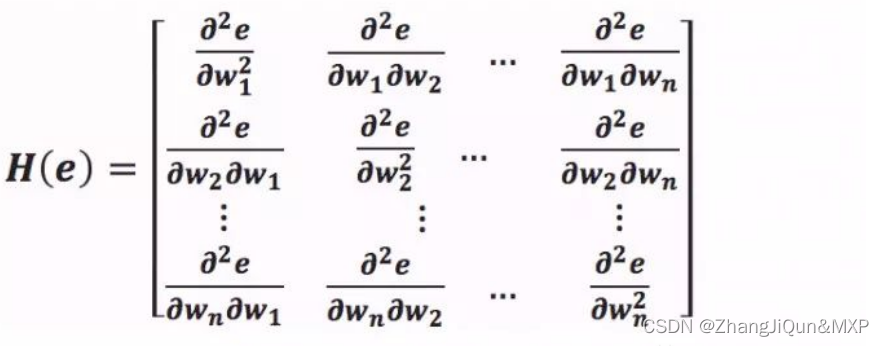
Hessian 矩阵给出了一个点的损失曲面曲率的估计。一个损失的表面可以有一个正曲率,这意味着当我们移动时,表面会迅速变得不那么陡峭。如果我们有一个负曲率,这意味着当我们移动时,曲面变得越来越陡。
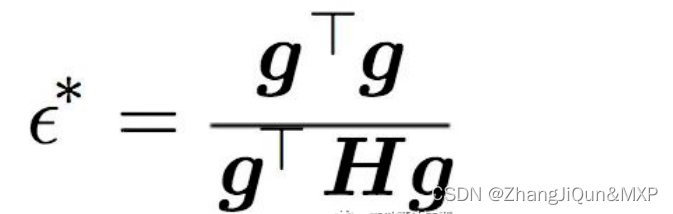
注意,如果这一步是负的,那就意味着我们可以使用任意的步骤。换句话说,我们可以切换回原来的算法。这对应于下面的情况,梯度变得越来越陡。
然而,如果梯度变得不那么陡峭,我们可能会走向一个处于病态曲率底部的区域。在这里,牛顿法给了我们一个修正的学习步骤,正如你所看到的,它与曲率成反比,或者曲面变得越来越小。
如果表面变得不那么陡峭,那么学习步骤就会减少。
2 Momentum:动量
与 SDG 结合使用的一种常用方法叫做 Momentum。Momentum 不仅会使用当前梯度,还会积累之前的梯度以确定走向。梯度下降方程修改如下。
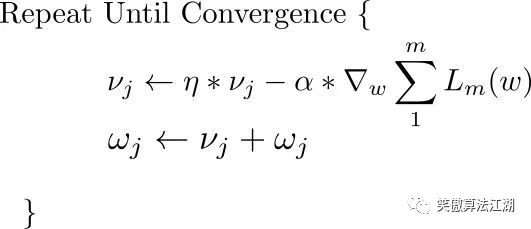
第一个式子有两项。第一项是上一次迭代的梯度,乘上一个被称为「Momentum 系数」的值,可以理解为取上次梯度的比例。

我们设 v 的初始为 0,动量系数为 0.9,那么迭代过程如下:
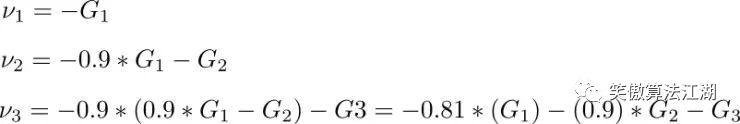
我们可以看到之前的梯度会一直存在后面的迭代过程中,只是越靠前的梯度其权重越小。(说的数学一点,我们取的是这些梯度步长的指数平均)。
这对我们的例子有什么帮助呢?观察下图,注意到大部分的梯度更新呈锯齿状。我们也注意到,每一步的梯度更新方向可以被进一步分解为 w1 和 w2 分量。如果我们单独的将这些向量求和,沿 w1 方向的的分量将抵消,沿 w2 方向的分量将得到加强。

3Adam
到目前为止,我们已经对比了 RMSProp 和 Momentum 两种方法。尽管 Momentum 加速了我们对极小值方向的搜索,但 RMSProp 阻碍了我们在振荡方向上的搜索。
Adam 或 Adaptive Moment Optimization:自适应力矩优化. 算法将 Momentum 和 RMSProp 两种算法结合了起来。这里是迭代方程。

我们计算了每个梯度分量的指数平均和梯度平方指数平均(方程 1、方程 2)。为了确定迭代步长我们在方程 3 中用梯度的指数平均乘学习率(如 Momentum 的情况)并除以根号下的平方指数平均(如 Momentum 的情况),然后方程 4 执行更新步骤。
超参数 beta1 一般取 0.9 左右,beta_2 取 0.99。Epsilon 一般取1e-10。
「结论」
在这篇文章中,我们介绍了 3 种基于梯度下降法来解决病态曲率同时加快搜索速度的方法。这些方法通常称为「自适应方法」,因为学习步骤会根据等高线拓扑进行调整。
在上面的三种方法中,尽管 Adam 算法在论文中被认为是最有前景的算法,但是 Momentum 方法貌似更主流一些。实践结果表明,在给定损失函数的情况下,三种算法都能收敛到不同的局部最优极小值。但是用带 Momentum 的 SGD 算法比 Adam 算法找到的极小值更加平坦,而自适应方法往往会收敛到更加尖锐的极小值点。平坦的极小值通常好于尖锐的极小值。
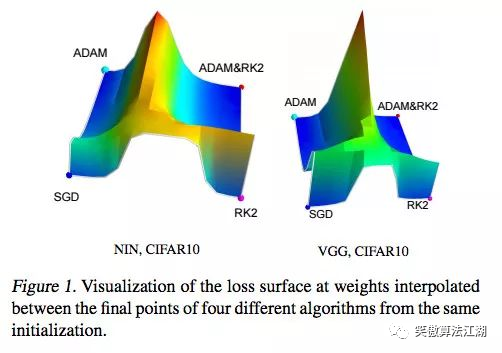
尽管自适应算法有助于我们在复杂的损失函数上找到极小值点,但这还不够,特别是在当前网络越来越来越深的背景下。除了研究更好的优化方法之外,还有一些研究致力于构建产生更平滑损失函数的网络架构。Batch-Normalization 和残差连接是其中的解决方法,我们也会尽快在博客上发布有关的详细介绍。欢迎随时在评论中提问。
相关文章:

深度学习优化入门:Momentum、RMSProp 和 Adam
目录 深度学习优化入门:Momentum、RMSProp 和 Adam 病态曲率 1牛顿法 2 Momentum:动量 3Adam 深度学习优化入门:Momentum、RMSProp 和 Adam 本文,我们讨论一个困扰神经网络训练的问题,病态曲率。 虽然局部极小值和鞍点会阻碍…...

LeetCode 面试题 01.09. 字符串轮转
文章目录 一、题目二、C# 题解 一、题目 字符串轮转。给定两个字符串 s1 和 s2,请编写代码检查 s2 是否为 s1 旋转而成(比如,waterbottle 是 erbottlewat 旋转后的字符串)。 点击此处跳转题目。 示例1: 输入:s1 “wa…...

系统上线安全测评需要做哪些内容?
电力信息系统、航空航天、交通运输、银行金融、地图绘画、政府官网等系统再正式上线前需要做安全测试。避免造成数据泄露从而引起的各种严重问题。 那么系统上线前需要做哪些测试内容呢?下面由我给大家介绍 1、安全机制检测-应用安全 身份鉴别 登录控制模块 应提供…...
vue 中 axios 的安装及使用
vue 中 axios 的安装及使用 1. axios 安装2. axios使用 1. axios 安装 首先,打开当前的项目终端,输入 npm install axios --save-dev验证是否安装成功,检查项目根目录下的 package.json,其中的 devDependencies 里面会多出一个axios及其版本…...

数据结构——线性数据结构(数组,链表,栈,队列)
文章目录 1. 数组2. 链表2.1. 链表简介2.2. 链表分类2.2.1. 单链表2.2.2. 循环链表2.2.3. 双向链表2.2.4. 双向循环链表 2.3. 应用场景2.4. 数组 vs 链表 3. 栈3.1. 栈简介3.2. 栈的常见应用常见应用场景3.2.1. 实现浏览器的回退和前进功能3.2.2. 检查符号是否成对出现3.2.3. 反…...
多态(C++)
多态 一、初识多态概念“登场”1>. 多态的构成条件2>. 虚函数3>. 虚函数重写(覆盖)4>. 虚函数重写的两个例外1. 协变 一 基类和派生类虚函数返回值类型不同2. 析构函数重写(基类和派生类析构函数名不同) 小结 二、延伸…...

算法leetcode|73. 矩阵置零(rust重拳出击)
文章目录 73. 矩阵置零:样例 1:样例 2:提示:进阶: 分析:题解:rust:go:c:python:java: 73. 矩阵置零: 给定一个 m x n 的矩…...

axios 二次封装
axios 二次封装 基本上每一个项目开发,都必须要二次封装 axios。主要是为了减少重复性工作,不可能每一次发起新请求时,都要重新配置请求域名、请求头 Content-Type、Token 等信息。所以需要把公用的部分都封装成一个函数,每次调用…...

Rust安全之数值
文章目录 数值溢出 数值溢出 编译通过,运行失败 cargo run 1 fn main() {let mut arg std::env::args().skip(1).map(|x| x.parse::<i32>().unwrap()).next().unwrap();let m_i i32::MAX - 1;let a m_i arg;println!("{:?}", a); }thread main panicked…...

4种方法实现html 页面内锚点定位及跳转
使用scrollIntoView进行锚点定位效果 不知道你有没有遇到这样的需求:锚点定位?进入页面某个元素需要出现在可视区?…这一类的需求归根结底就是处理元素与可视区域的关系。我接触了很多前端小伙伴,实现的方式有各种各样的ÿ…...

gitlab配置备忘
版本 gitlab 14.6.2 gitlab备份上传到阿里云oss ### Backup Settings ###! Docs: https://docs.gitlab.com/omnibus/settings/backups.html# gitlab_rails[manage_backup_path] true # gitlab_rails[backup_path] "/var/opt/gitlab/backups"###! Docs: https://…...

基于Centos搭建k8s仓库
系统环境: Red Hat Enterprise Linux 9.1 (Plow) Kernel: Linux 5.14.0-162.6.1.el9_1.x86_64 主机名地址master192.168.19.128node01192.168.19.129node02192.168.19.130 目录 1、关闭防火墙,关闭SElinxu ,开启时间同步服务 2、关…...
浅谈泛在电力物联网发展形态与技术挑战
安科瑞 华楠 摘 要:泛在电力物联网是当前智能电网发展的一个方向。首先,总结了泛在电力物联网的主要作用和价值体现;其次,从智能电网各个环节概述了物联网技术在电力领域的已有研究和应用基础;进而,构思并…...

git reset --soft 用法
git reset --soft 是 Git 命令中的一个选项,它用于取消之前的提交,并将取消的更改保留在暂存区。这允许您重新组织提交历史或将更改合并到一个新的提交中,而不影响暂存区和工作目录中的更改。 这个命令的语法是: git reset --so…...

哪些测试仪器可以用于检测静电中和设备的性能
静电设备性能测试通常需要使用一些专门的仪器来进行。以下是一些常见的静电设备性能测试仪器: 1. 静电电压测试仪:用于测量物体表面的静电电压。它通常可以测量正负电压,并具有高精度和快速响应的特点。 2. 静电电荷仪:用于测量物…...

浅析 GlusterFS 与 JuiceFS 的架构异同
在进行分布式文件存储解决方案的选型时,GlusterFS 无疑是一个不可忽视的考虑对象。作为一款开源的软件定义分布式存储解决方案,GlusterFS 能够在单个集群中支持高达 PiB 级别的数据存储。自从首次发布以来,已经有超过十年的发展历程。目前&am…...
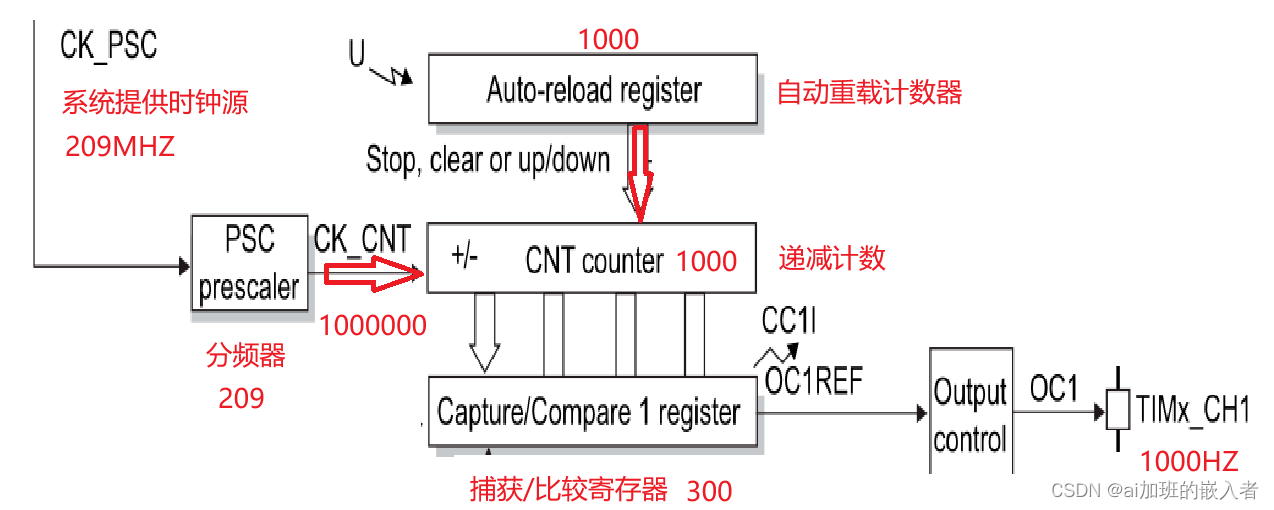
ARM开发,stm32mp157a-A7核PWM实验(驱动蜂鸣器,风扇,马达工作)
1.分析框图; 2.比较捕获寄存器(产生PWM方波); 工作原理: 1、系统提供一个时钟源209MHZ,需要通过分频器进行分频,设置分频器值为209分频; 2、当定时器启动之后,自动重载…...
|消费者需求研究方案)
群狼调研(长沙眼镜店神秘顾客)|消费者需求研究方案
本文由群狼调研(长沙品牌调研)出品,欢迎转载,请注明出处。消费者需求研究方案是在开展研究之前制定的计划,用于指导研究的设计、实施和分析。以下是一个可能的消费者需求研究方案的大致框架: 1. 研究目标和问题: • …...

电脑入门:宽带路由器常见故障排除技巧
宽带路由器在企业网络中的应用是相当广泛的,在运行的过程中出现故障是在所难免的,虽然故障现象多种多样,引起故障发生的原因也不尽相同,但从大体上可以把这些故障分为硬件故障和软件故障,具体来说就是一些网络连接性问题、配置文件选项问题以及网络协议问题等。 由于路由器…...

基于云原生网关的流量防护实践
作者:涂鸦 背景 在分布式系统架构中,每个请求都会经过很多层处理,比如从入口网关再到 Web Server 再到服务之间的调用,再到服务访问缓存或 DB 等存储。在下图流量防护体系中,我们通常遵循流量漏斗原则进行流量防护。…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
