【赋权算法】Python实现熵权法
在开始之前,我们先说一下信息熵的概念。
当一件事情发生,如果是意料之中,那么这个事情就并不能拿来当做茶余饭后的谈资,我们可以说这个事情并没有什么信息和价值。而当一件不可能发生的事情发生的时候,我们可能就会觉得震撼三观,这件事情太Crazy了,带来的信息量也就很多。
哼哼,通过上文我们可以知道,一个事情越稳定,信息量就越少,那么如何去衡量呢?我们可以用概率的倒数(也就是负相关)来衡量。
I = − l o g ( p ( x ) ) I=-log(p(x)) I=−log(p(x))
I I I也就是自信息,一件事情越确定,自信息也就越小。
而信息熵就是自信息的期望,代表这一件事情的混乱程度。信息熵越大,混乱程度越大,说明这件事情越疯狂。
H = − l o g ( p ( x ) ) p ( x ) H=-log(p(x))p(x) H=−log(p(x))p(x)
再说熵权法(Entropy Weight Method),熵权法是客观赋权的一种方式,对应的主观赋权有专家打分法,相似的还有层次分析法。熵权法是利用信息稳定程度而提出的方法,一般来说,某列属性越稳定,它的信息就越可信,那么在实际的权重也应当越高。
不说人话,那就是:
一般来说,若某个指标的信息熵越小,表明指标值得变异程度越大,提供的信息量越多,在综合评价中所能起到的作用也越大,其权重也就越大。相反,某个指标的信息熵越大,表明指标值得变异程度越小,提供的信息量也越少,在综合评价中所起到的作用也越小,其权重也就越小。
你会发现在这段话中,自信息和提供信息实际上是成反比的。
不管他,只需要知道原本越稳定的数据,对异常越敏感,也越可信。
在实际计算中,遵循以下步骤:
step1 归一化
正向指标
Y i j = X i j − m i n ( X i ) m a x ( X i ) − m i n ( X i ) Y_{ij}=\frac{X_{ij}-min(X_i)}{max(X_i)-min(X_i)} Yij=max(Xi)−min(Xi)Xij−min(Xi)
负向指标
Y i j = m a x ( X i ) − X i j m a x ( X i ) − m i n ( X i ) Y_{ij}=\frac{max(X_i)-X_{ij}}{max(X_i)-min(X_i)} Yij=max(Xi)−min(Xi)max(Xi)−Xij
step2 求频率替换概率
p i j = Y i j ∑ Y i j p_{ij}=\frac{Y_{ij}}{\sum Y_{ij}} pij=∑YijYij
step3 计算归一化信息熵
E n t r o p y = − 1 l n ( n ) ∑ p i j l n ( p i j ) Entropy=-\frac{1}{ln(n)}\sum p_{ij}ln(p_{ij}) Entropy=−ln(n)1∑pijln(pij)
以什么为底的不重要啦
step4 计算权重
W j = 1 − E j k − ∑ E j W_j=\frac{1-E_j}{k-\sum E_j} Wj=k−∑Ej1−Ej
以下是实现代码:
def EWM(data):t=(data-data.min(axis=0))/(data.max(axis=0)-data.min(axis=0))t=t/t.sum(axis=0)t[t<0.0001]=0.0001entropy=-1/np.log(t.shape[0])*np.sum(t*np.log(t))return [(1-i)/(len(entropy)-sum(entropy)) for i in entropy]
当然,这样的结果只是个权重,我们还需要对数据做乘法:
np.matmul(data.values,np.array(EWM(data)).T)

对这样一组数据,A十分稳定,B是正态分布,C是二分布,得到的结果是:
信息熵:

权重:
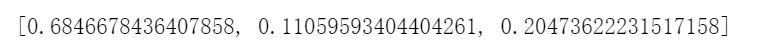
确实符合越稳定权重越大。
熵权法的优点
熵值法是根据各项指标指标值的变异程度来确定指标权数的,这是一种客观赋权法,避免了人为因素带来的偏差。
相对那些主观赋值法,精度较高客观性更强,能够更好的解释所得到的结果。
熵权法的缺点
忽略了指标本身重要程度,有时确定的指标权数会与预期的结果相差甚远,同时熵值法不能减少评价指标的维数,也就是熵权法符合数学规律具有严格的数学意义,但往往会忽视决策者主观的意图;
如果指标值的变动很小或者很突然地变大变小,熵权法用起来有局限
相关文章:
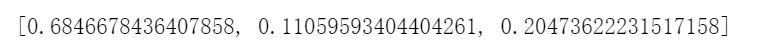
【赋权算法】Python实现熵权法
在开始之前,我们先说一下信息熵的概念。 当一件事情发生,如果是意料之中,那么这个事情就并不能拿来当做茶余饭后的谈资,我们可以说这个事情并没有什么信息和价值。而当一件不可能发生的事情发生的时候,我们可能就会觉…...

docker之 Consul(注册与发现)
目录 一、什么是服务注册与发现? 二、什么是consul 三、consul 部署 3.1建立Consul服务 3.1.1查看集群状态 3.1.2通过 http api 获取集群信息 3.2registrator服务器 3.2.1安装 Gliderlabs/Registrator 3.2.2测试服务发现功能是否正常 3.2.3验证 http 和 ng…...

用NeRFMeshing精确提取NeRF网络中的3D网格
准确的 3D 场景和对象重建对于机器人、摄影测量和 AR/VR 等各种应用至关重要。 NeRF 在合成新颖视图方面取得了成功,但在准确表示底层几何方面存在不足。 推荐:用 NSDT编辑器 快速搭建可编程3D场景 我们已经看到了最新的进展,例如 NVIDIA 的…...
权限提升-Windows本地提权-AT+SC+PS命令-进程迁移-令牌窃取-getsystem+UAC
权限提升基础信息 1、具体有哪些权限需要我们了解掌握的? 后台权限,网站权限,数据库权限,接口权限,系统权限,域控权限等 2、以上常见权限获取方法简要归类说明? 后台权限:SQL注入,数…...
深入了解Kubernetes(k8s):安装、使用和Java部署指南(持续更新中)
目录 Docker 和 k8s 简介1、kubernetes 组件及其联系1.1 Node1.2 Pod1.3 Service 2、安装docker3、单节点 kubernetes 和 KubeSphere 安装3.1 安装KubeKey3.2 安装 kubernetes 和 KubeSphere3.3 验证安装结果 4、集群版 kubernetes 和 KubeSphere 安装5、kubectl 常用命令6、资…...
Oracle的学习心得和知识总结(二十九)|Oracle数据库数据库回放功能之论文三翻译及学习
目录结构 注:提前言明 本文借鉴了以下博主、书籍或网站的内容,其列表如下: 1、参考书籍:《Oracle Database SQL Language Reference》 2、参考书籍:《PostgreSQL中文手册》 3、EDB Postgres Advanced Server User Gui…...

新版100句学完7000雅思单词
新版100句学完7000雅思单词 1. As the medical world continues to grapple with what’s acceptable and what’s not, it is clear that companies must continue to be heavily scrutinized for their sales and marketing strategies.(剑桥雅思6) 随着医学界持续努力解决…...
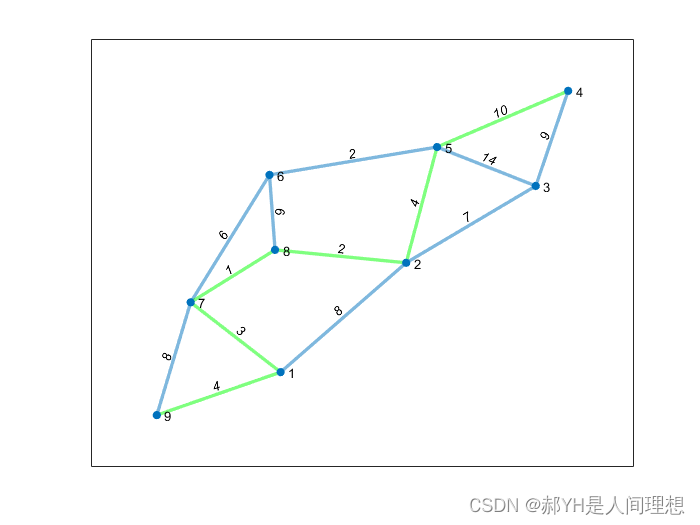
MATLAB图论合集(三)Dijkstra算法计算最短路径
本贴介绍最短路径的计算,实现方式为迪杰斯特拉算法;对于弗洛伊德算法,区别在于计算了所有结点之间的最短路径,考虑到MATLAB计算的便捷性,计算时只需要反复使用迪杰斯特拉即可,暂不介绍弗洛伊德的实现 迪杰斯…...

MySQL 8.0.xx 版本解决group by分组的问题
因为版本升级5.7版本以下是没有这个问题的,8.0版本以上会出现分组问题 1055 - Expression #1 of SELECT list is not in GROUP BY clause and contains nonaggregated column test1.sys_t.id which is not functionally dependent on columns in GROUP BY clause; t…...
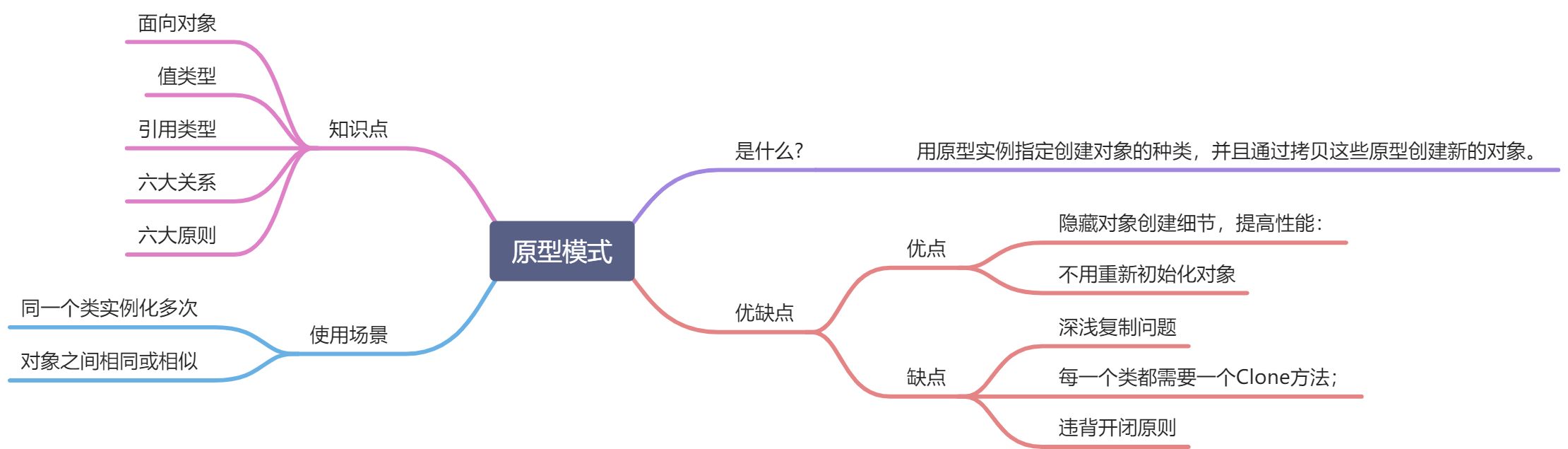
设计模式—原型模式(Prototype)
目录 一、什么是原型模式? 二、原型模式具有什么优缺点吗? 三、有什么缺点? 四、什么时候用原型模式? 五、代码展示 ①、简历代码初步实现 ②、原型模式 ③、简历的原型实现 ④、深复制 ⑤、浅复制 一、什么是原型模式&…...
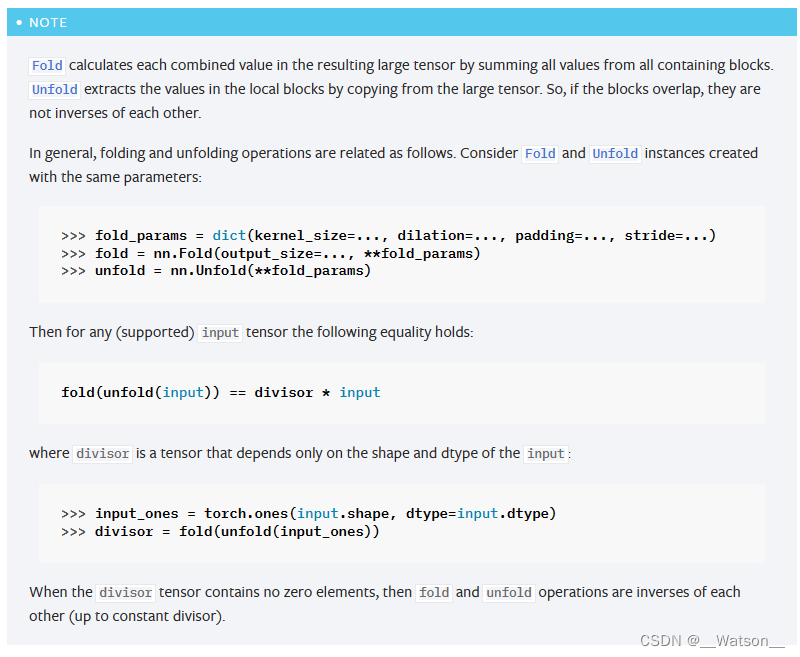
【pytorch】Unfold和Fold的互逆操作
1. 参数定义 Unfold https://pytorch.org/docs/stable/generated/torch.nn.Unfold.html#torch.nn.Unfold Fold https://pytorch.org/docs/stable/generated/torch.nn.Fold.html#torch.nn.Fold 注意:参数当中的padding是在四周边补零,而当fold后的尺寸…...

【AI】《动手学-深度学习-PyTorch版》笔记(二十一):目标检测
AI学习目录汇总 1、简述 通过前面的学习,已经了解了图像分类模型的原理及实现。图像分类是假定图像中只有一个目标,算法上是对整个图像做的分类。 下面我们来学习“目标检测”,即从一张图像中找出需要的目标,并标记出位置。 2、边界框 边界框:bounding box,就是一个方…...
畅捷通T+用户中locked勒索病毒后该怎么办?勒索病毒解密数据恢复
Locked勒索病毒是一种近年来在全球范围内引起广泛关注的网络安全威胁程序。它是一种加密货币劫持病毒,专门用于加密用户的数据并要求其支付赎金。Locked勒索病毒通过攻击各种系统漏洞和网络薄弱环节,使用户计算机受到感染并被加密锁定时,无法…...
神仙般的css动画参考网址,使用animate.css
Animate.css | A cross-browser library of CSS animations.Animate.css is a library of ready-to-use, cross-browser animations for you to use in your projects. Great for emphasis, home pages, sliders, and attention-guiding hints.https://animate.style/这里面有很…...

江西抚州新能源汽车3d扫描零部件逆向抄数测量改装-CASAIM中科广电
汽车改装除了在外观方面越来越受到消费者的青睐,在性能和实用性提升上面的需求也是日趋增多,能快速有效地对客户指定汽车零部件进行一个改装,是每一个汽车改装企业和工程师的追求,也是未来消费者个性化差异化的要求。下面CASAIM中…...
数据结构学习 --4 串
数据结构学习 --1 绪论 数据结构学习 --2 线性表 数据结构学习 --3 栈,队列和数组 数据结构学习 --4 串 数据结构学习 --5 树和二叉树 数据结构学习 --6 图 数据结构学习 --7 查找 数据结构学习 --8 排序 本人学习记录使用 希望对大家帮助 不当之处希望大家帮忙纠正…...

探索Kotlin K2编译器和Java编译器的功能和能力
文章首发地址 Kotlin K2编译器是Kotlin语言的编译器,负责将Kotlin源代码转换为Java字节码或者其他目标平台的代码。K2编译器是Kotlin语言的核心组件之一,它的主要功能是将Kotlin代码编译为可在JVM上运行的字节码。 K2编译器快速介绍 编译过程ÿ…...

如何安装chromadb
下载最新版本的python3.10 因为chromadb需要sqlite3的最小版本是3.35.0 使用如下命令安装 pip install chromadb 安装完毕后在python3的命令行窗口输入 import chromadb 如果不报错代表成功,如果报错sqlite3的最小版本是3.35.0,使用如下方式解决 …...

vue实现把字符串中的所有@内容,替换成带标签的
前言: 目前有个需求是,要把输入框里面的还有姓名高亮。 要求: 1、必须用 v-html ,带标签的给他渲染 2、把字符串中的全部查找出来,替换掉,注意要过滤已经替换好的,不然就是无限循环了 实现方法:…...

「MySQL-00」MySQL在Linux上的安装、登录与删除
目录 一、安装MySQL 0. 安装前请先执行一遍删除操作,把预装或残留的MySQL删除掉 1. 安装yum源 (解决了在哪里找MySQL的问题) 2. 安装哪个版本的MySQL 二、启动和登录MySQL 三、删除MySQL / MariaDB 安装与卸载前,建议先将用户切换…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
