Metasploit“MSF”连接postgresql时因排序规则版本不匹配导致无法连接
一、问题
更新Kali之后使用Metasploit时出现一个问题,连接postgresql时因排序规则版本不匹配导致无法连接
警告: database "msf" has a collation version mismatch
DETAIL: The database was created using collation version 2.36, but the operating system provides version 2.37.
HINT: Rebuild all objects in this database that use the default collation and run ALTER DATABASE msf REFRESH COLLATION VERSION, or build PostgreSQL with the right library version.
其实就是换了一个2.37的版本,可能更新的时候版本未进行同步问题
二、解决方法
sudo -u postgres psql -U postgres -d msf
REINDEX DATABASE msf;
ALTER DATABASE msf REFRESH COLLATION VERSION;
相关文章:

Metasploit“MSF”连接postgresql时因排序规则版本不匹配导致无法连接
一、问题 更新Kali之后使用Metasploit时出现一个问题,连接postgresql时因排序规则版本不匹配导致无法连接 警告: database "msf" has a collation version mismatch DETAIL: The database was created using collation version 2.36, but the operati…...
)
CCF CSP题解:矩阵运算(202305-2)
链接和思路 OJ链接:传送门 本题要求计算1个公式: ( W ⋅ ( Q K T ) ) V \left(\mathbf{W} \cdot (\mathbf{Q} \times \mathbf{K}^{T})\right) \times \mathbf{V} (W⋅(QKT))V 其中, Q \mathbf{Q} Q、 K \mathbf{K} K和 V \mathbf{V} V均…...
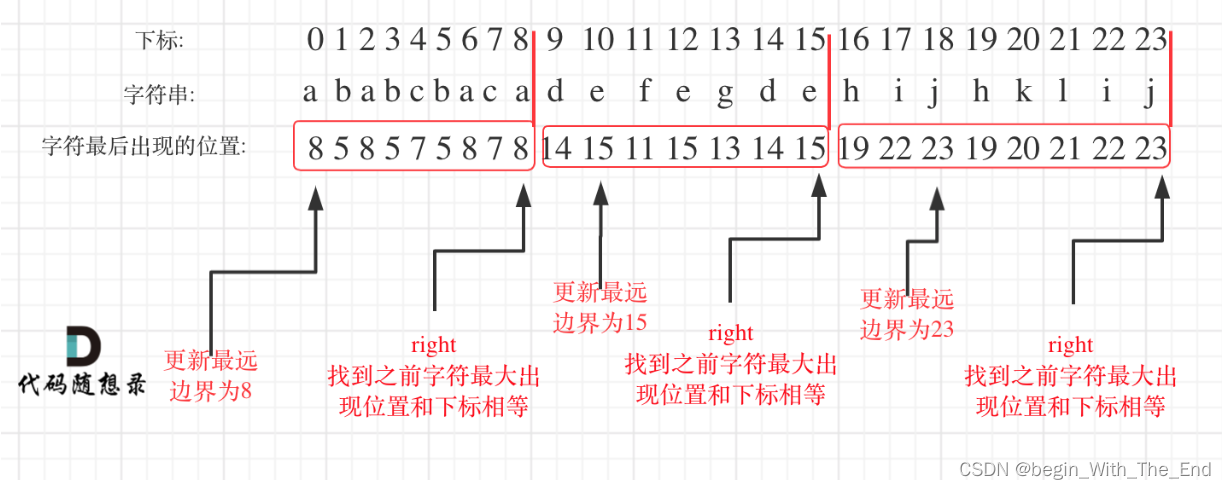
划分字母区间【贪心算法】
划分字母区间 给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。 注意,划分结果需要满足:将所有划分结果按顺序连接,得到的字符串仍然是 s 。返回一个表示每个字符串片段的长度的列表。…...

低代码的探索之路
Gartner发布报告指出,2023年全球低代码开发平台市场规模将达到345亿美元,比2022年增长20%。 目前,国内外已经有许多低代码平台,包括OutSystems、Mendix、Appian、Microsoft Power App等。这些平台提供了丰富的功能和工具ÿ…...

easyUI combobox不可手动输入和禁用
combobox //下拉可用 $("#selectId").combobox(enable); //下拉不可用 $("#selectId").combobox(disable); //该元素可用 $("#selectId").combobox({ disabled: false }); //该元素不可用 $("#selectId").combobox({ disabled: tru…...
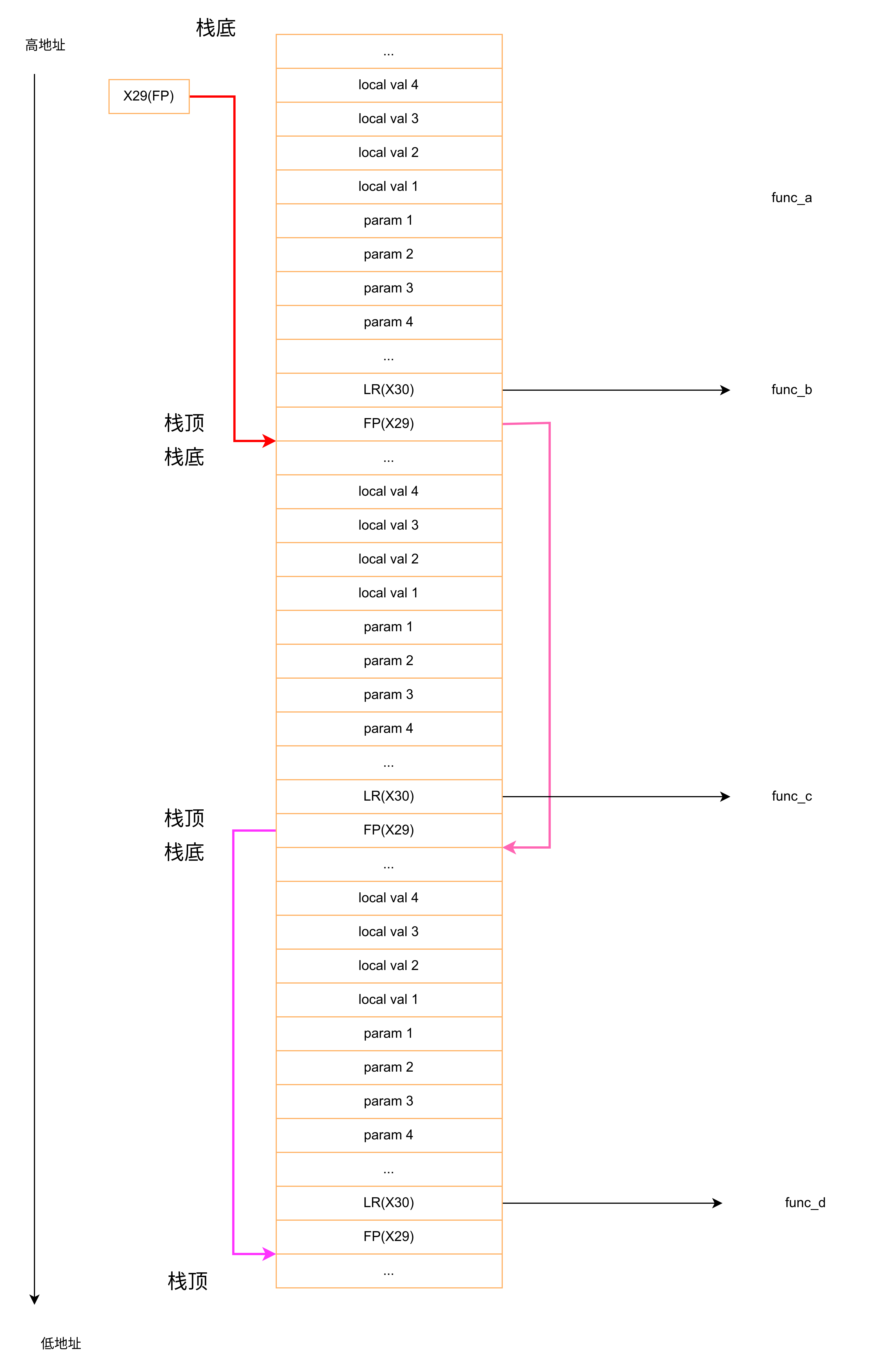
RV64和ARM64栈结构差异
RV64和ARM64栈结构差异 1 RV64和ARM64栈结构差异示意图1.1 RV64和ARM64寄存器介绍1.1.1 RV64寄存器1.1.2 ARM64寄存器 1.2 RV64和ARM64栈结构差异示意图 2 RV64和ARM64栈使用示例2.1 测试的程序2.2 RV64反汇编的汇编程序2.3 ARM64反汇编的汇编程序2.4 RV64和ARM64测试程序的栈结…...
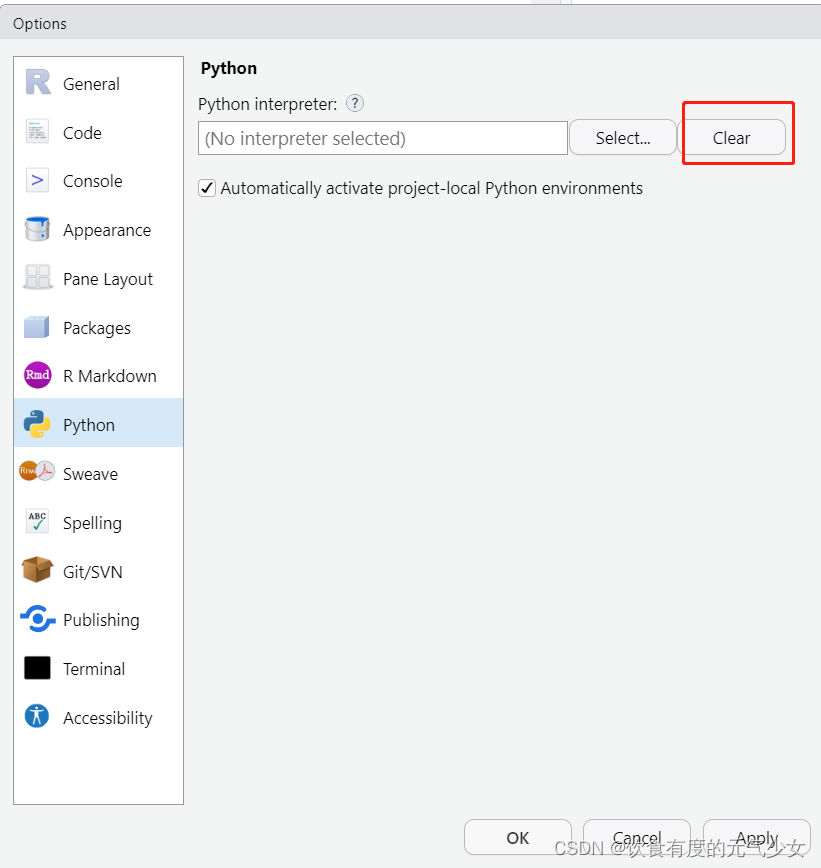
将 Python 与 RStudio IDE 配合使用(R与Python系列第一篇)
目录 前言: 1-安装reticulate包 2-安装Python 3-选择Python的默认版本(配置Python环境) 4-使用Python 4.1 运行一个简单的Python脚本 4.2 在RStudio上安装Python模块 4.3 在 R 中调用 Python 模块 4.4 在RStudio上调用Python脚本写的…...

数据库访问性能优化
目录 IO性能分析数据库性能优化漏斗法则1、减少数据访问(减少磁盘访问)(1) 正确的创建并使用索引索引生效场景索引失效场景判断索引是否生效--执行计划 2、返回更少数据(减少网络传输或磁盘访问)(1) 数据分页处理(减少行数)客户端…...

vue 预览 有token验证的 doc、docx、pdf、xlsx、csv、图片 并下载
预览 doc我也不会 //docx <div v-if"previewType docx" ref"iframeDom" style"border: none; width: 100%; height: 100%"></div> import { renderAsync } from "docx-preview"; let iframeDom: any ref(); axios({url…...

WPF数据视图
将集合绑定到ItemsControl控件时,会不加通告的在后台创建数据视图——位于数据源和绑定的控件之间。数据视图是进入数据源的窗口,可以跟踪当前项,并且支持各种功能,如排序、过滤、分组。 这些功能和数据对象本身是相互独立的&…...

C++ new/delete 与 malloc/free 的区别?
new/delete 与 malloc/free 的区别? 分配内存的位置 malloc是从堆上动态分配内存new是从自由存储区为对象动态分配内存。自由存储区的位置取决于operator new的实现。自由存储区不仅可以为堆,还可以是静态存储区,这都看operator new在哪里为…...
【数学建模】常微分,偏微分方程
1.常微分方程 普通边界 已知t0时刻的初值 ode45() 龙格-库塔法 一阶,高阶都一样 如下: s(1) y , s(2)y s(3) x , s(4)x //匿名函数 下为方程组 核心函数 s_chuzhi [0;0;0;0]; //初值 分别两个位移和速度的初值 t0 0:0.2:180; f (t,s)[s(2);(…...

浙大数据结构之09-排序1 排序
题目详情: 给定N个(长整型范围内的)整数,要求输出从小到大排序后的结果。 本题旨在测试各种不同的排序算法在各种数据情况下的表现。各组测试数据特点如下: 数据1:只有1个元素;数据2…...

Pydantic 学习随笔
这里是零散的记录一些学习过程中随机的理解,因此这里的记录不成体系。如果是想学习 Pydantic 建议看官方文档,写的很详细并且成体系。如果有问题需要交流,欢迎私信或者评论。 siwa 报 500 Pydantic 可以和 siwa 结合使用,这样既…...
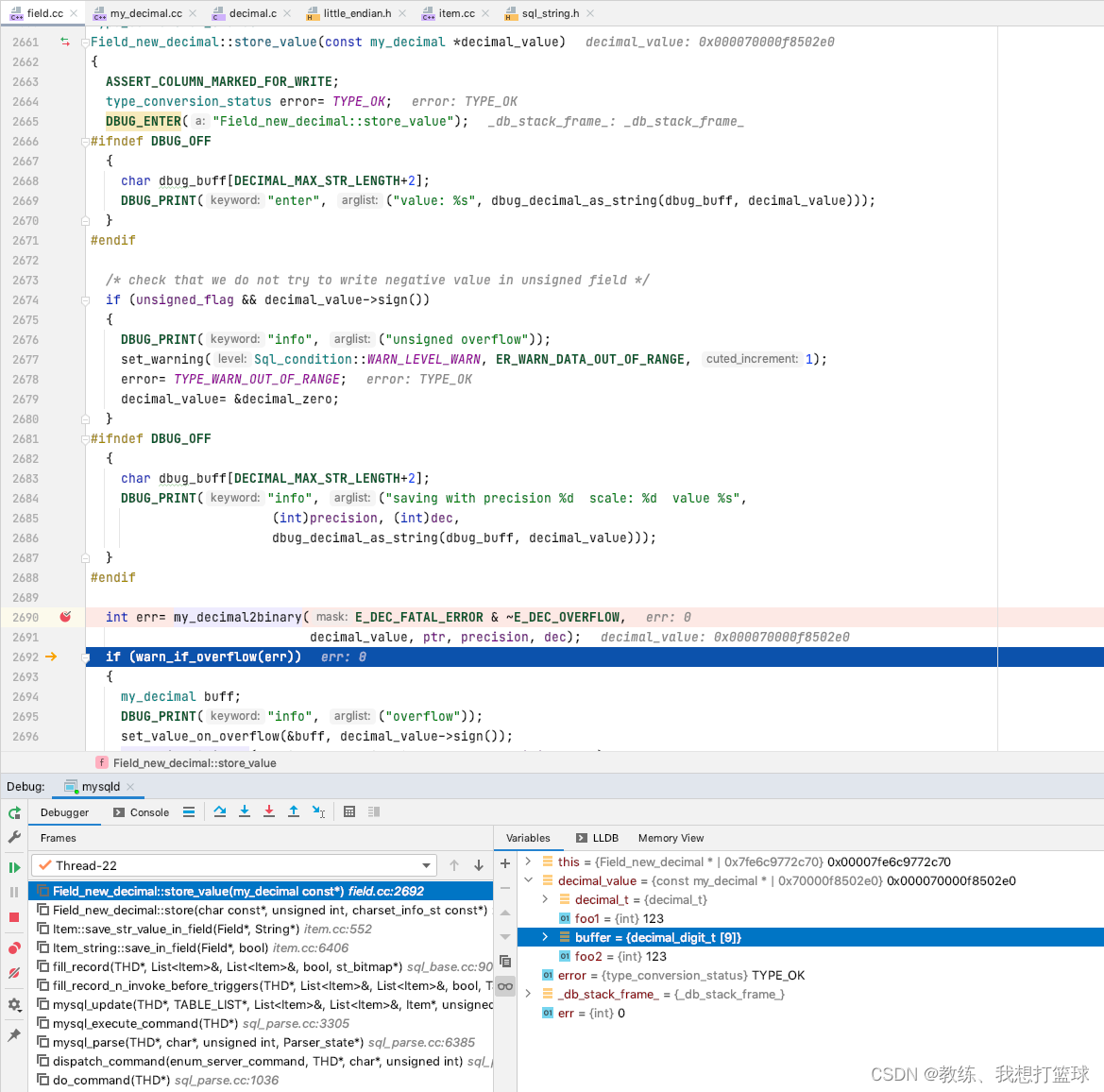
11 mysql float/double/decimal 的数据存储
前言 这里主要是 由于之前的一个 datetime 存储的时间 导致的问题的衍生出来的探究 探究的主要内容为 int 类类型的存储, 浮点类类型的存储, char 类类型的存储, blob 类类型的存储, enum/json/set/bit 类类型的存储 本文主要 的相关内容是 float, decimal 类类型的相关数据…...

【高效数据结构——位图bitmap】
初识位图bitmap 位图(Bitmap)是一种用于表示和操作位(bit)的数据结构。它是由一系列二进制位(0 或 1)组成的序列,每个位都可以单独访问和操作。 位图常用于以下情况: 压缩存储&…...

ArrayList LinkedList
ArrayList 和 LinkedList 区别 ArrayList和LinkedList都是Java集合框架中的实现类,用于存储和操作数据。它们在底层实现和性能特点上有一些区别。 数据结构:ArrayList底层使用数组实现,而LinkedList底层使用双向链表实现。这导致它们在内存结…...
iOS砸壳系列之三:Frida介绍和使用
当涉及从App Store下载应用程序时,它们都是已安装的iOS应用(IPA)存储在设备上。这些应用程序通常带有保护的代码和资源,以限制用户对其进行修改或者逆向工程。 然而,有时候,为了进行调试、制作插件或者学习…...
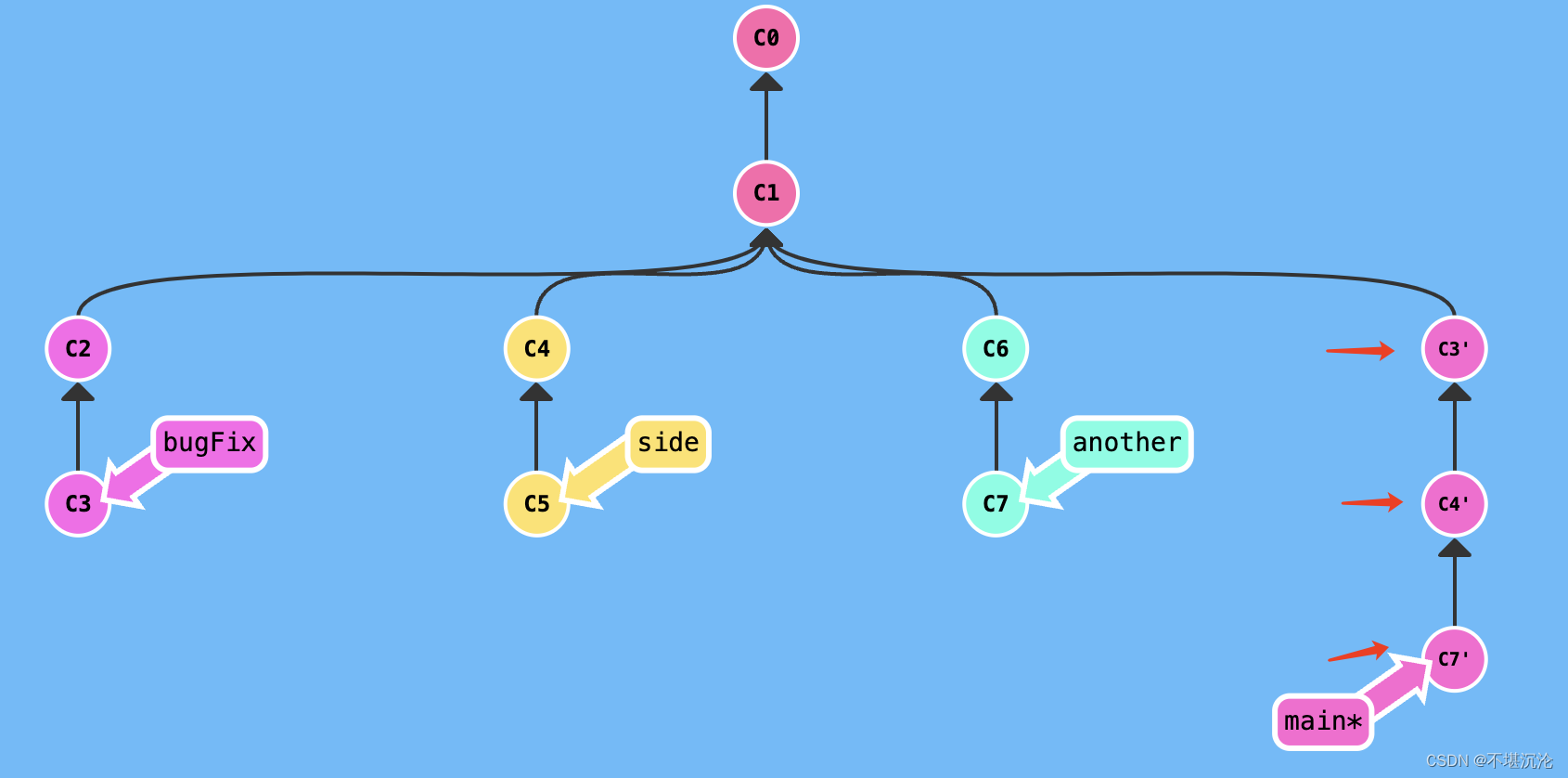
Git学习——细节补充
Git学习——细节补充 1. git diff2. git log3. git reset4. git reflog5. 提交撤销5.1 当你改乱了工作区某个文件的内容,想直接丢弃工作区的修改时5.2 当提交到了stage区后,想要退回 6. git remote7. git pull origin master --no-rebase8. 分支管理9. g…...

【设计模式】Head First 设计模式——装饰者模式 C++实现
设计模式最大的作用就是在变化和稳定中间寻找隔离点,然后分离它们,从而管理变化。将变化像小兔子一样关到笼子里,让它在笼子里随便跳,而不至于跳出来把你整个房间给污染掉。 设计思想 动态地将责任附加到对象上,若要扩…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
