LightGBM
目录
1.LightGBM的直方图算法(Histogram)
直方图做差加速
2.LightGBM得两大先进技术(GOSS&EFB)
2.1 单边梯度抽样算法(GOSS)
2.2 互斥特征捆绑算法(EFB)
3.LightGBM得生长策略(leaf-wise)
通过与xgboost对比,在这里列出lgb新提出的几个方面的技术
1.LightGBM的直方图算法(Histogram)
LightGBM里面的直方图算法是为了减少分裂点的数量。
直方图就是把连续的浮点特征离散化为k个整数(也就是分桶bins的思想),比如[0,0.1)->0,[0.1,0.3)->1。并根据特征所在的bin对其进行梯度累加和个数统计,在遍历数据的时候,根据离散化后的值作为索引在直方图中累计统计量,当遍历一次数据后,直方图累积了需要的统计量,当遍历一次数据后,直方图累积了需要的统计量,然后根据直方图的离散值,遍历寻找最优的分割点。我们来形象化的画个图。

这样在遍历到该特征的时候,只需要根据直方图的离散值,遍历寻找最优的分割点即可,由于bins的数量是远小于样本不同取值的数量的,所以分桶之后要遍历的分裂点的个数会少了很多,这样就可以减少计算量。基于上面的这个方式,如果是把所有特征放到一块的话,应该是下面的这种感觉:

histogram算法还可以进一步加速。一个叶子节点的histogram可以直接由父节点的histogram和兄弟节点的histogram做差得到。一般情况下,构造histogram需要遍历该叶子上的所有数据,通过该方法,只需要遍历histogram的k个桶。
直方图做差加速
当节点分裂成两个时,右边的子节点的直方图其实等于父节点的直方图减去左边子节点的直方图:

再举个例子形象化的理解:
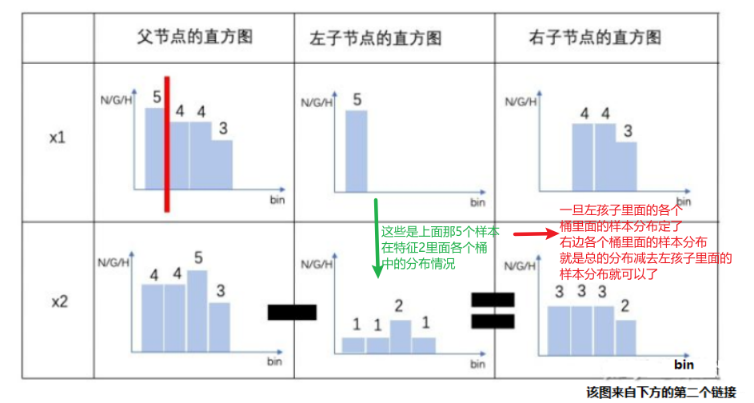
histogram算法并不是完美的。由于特征被离散化后,找到的并不是很精确的分割点,所以会对结果产生影响。但在实际的数据集上表明,离散化的分裂点对最终的精度影响并不大,甚至会好一些。原因在于decision tree本身就是一个弱学习器,分割点是不是精确并不是太重要,采用histogram算法会起到正则化的效果,有效地防止模型的过拟合(bin数量决定了正则化的程度,bin越少惩罚越严重,欠拟合风险越高) 。
因为xgboost的近似分割算法也用了分桶,这里和xgboost中的weight quantile sketch算法做一个比较,xgboost考虑的是对loss的影响权值,用的每个样本的hi来标识的,相当于基于hi的分布去找候选分割点,这样带来的一个问题就是每一层划分完了之后,下一次依然需要构建这样的直方图,毕竟样本被划分到了不同的节点中,二阶导分布也就变了。所以xgboost在每一层都得动态构建直方图,因为它这个直方图算法不是针对某个特定得feature得,而是所有feature共享一个直方图(每个样本权重得二阶导)。而lightgbm对每个特征都有一个直方图,这样构建一次就ok,并且分裂得时候还能通过直方图进行加速。故xgboost得直方图算法是不如lightgbm得直方图算法快得。
2.LightGBM得两大先进技术(GOSS&EFB)
接下来说lightgbm得两大先进技术(GOSS&EFB),这两大技术是lightgbm相对于xgboost独有得,分别是单边梯度抽样算法(GOSS)和互斥特征捆绑算法(EFB),GOSS可以减少样本得数量,而EFB可以减少特征得数量,这样就能降低模型分裂过程中得复杂度。
2.1 单边梯度抽样算法(GOSS)
goss通过减少样本数量去帮助lgb更快
单边梯度抽样算法(Gradient-based One-Side Sampling)是从减少样本得角度出发,排除大部分权重小得样本,仅用剩下得样本计算信息增益,它是一种在减少数据和保证精度上平衡得算法。
但是这个时候就有个问题权重从哪来,我们通过了解GBDT得原理,可以知道,在训练新模型得过程中,梯度比较小得样本对于降低残差得作用效果不是太大,所以我们可以关注梯度高得样本,这样就可以减少计算量了。这里我们再记录下为啥梯度小得样本对降低残差效果不大。
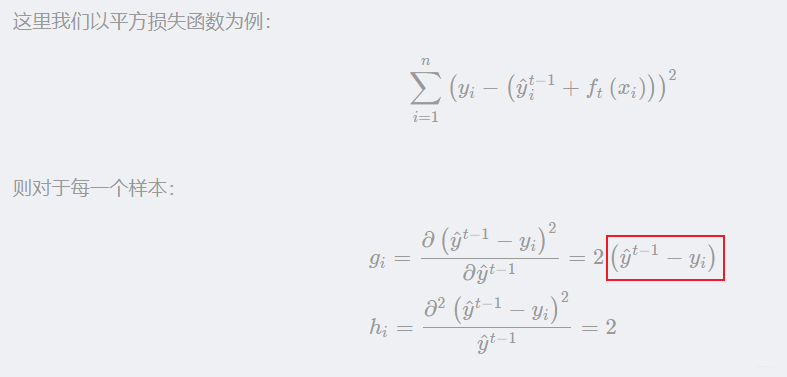
可以看到梯度就是残差得一个相反数,也就是
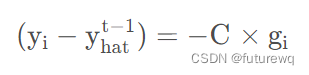
这个常数不用管,这样也就是说如果我新得模型想降低残差得效果好,那么样本得梯度应该越大越好,所以这就是为啥梯度小得样本对于降低残差得效果不大。也是为啥样本得梯度大小可以反映样本权重得原因。
但是要是盲目得直接去掉这些梯度小得数据,这样就会改变数据得分布了啊,所以lgb才提出了单边梯度抽样算法,根据样本得权重信息对样本进行抽样,减少了大量梯度小得样本,但是还能不会过多得改变数据集得分布。
GOSS算法保留了梯度大的样本,并对梯度小得样本进行随机抽样,为了不改变样本得数据分布,再计算增益时为梯度小得样本引入了一个常数进行平衡。具体:首先先根据样本得梯度对样本从大到小排序,然后拿到前a%得梯度大得样本,和剩下样本得b%,再计算增益时,后面得这b%通过乘上(1-a)/b来放大梯度小得样本得权重。一方面算法将更多得注意力放在训练不足得样本上,另一方面通过乘上权重来防止采样对原始数据分布造成太大得影响。
我们来看一个具体得例子:

通过上面,我们就通过采样得方式,选出了我们得样本,两个梯度大得6号和7号,然后又从剩下得样本里面随机选取了2个梯度小得,4号和2号,这时候我们看看goss算法怎么做:

这里得Ni是样本数,梯度小得样本乘上相应的权重之后,我们再基于采样样本得估计直方图中可以返现Ni得总个数依然是8个,虽然6个梯度小得样本中去掉了4个,留下了两个。但是这2个样本再梯度上和个数上都进行了3倍数得方法,所以可以防止采样对原始数据分布造成太大得影响。
2.2 互斥特征捆绑算法(EFB)
EFB是从减少特征的角度去帮助lgb更快。
高维度得数据往往是稀疏得,这种稀疏性启发我们设计一种无损得方法来减少特征的维度。通常被捆绑得特征都是互斥得,这样两个特征捆绑起来才会丢失信息。如果两个特征并不是完全互斥(部分情况下两个特征都是非零值),可以用一个指标对特征不互斥程度进行衡量,称之为冲突比率,当这个值较小时,我们可以选择把不完全互斥得两个特征捆绑,而不影响最后得精度。
举一个很极端得例子。

可以看到,每一个特征都只有一个训练样本时非0且都不是同一个训练样本,这样的话特征之间也没有冲突了。这样得情况就可以把这四个特征捆绑成一个,这样维度就减少了。
EFB指出如果将一些特征进行融合绑定,则可以降低特征数量。这样再构建直方图得时候时间复杂度从O(#data*#feature)变成O(#data*#bundle),这里得#bundle指的是特征融合后特征包得个数,且#bundle<<#feature。针对这个特征捆绑融合,有两个问题需要解决。
- 怎么判断哪些特征应该绑在一起?
- 特征绑在一起之后,特征值应该如何确定呢?
对于问题一,EFB算法利用特征和特征间得关系构造一个加权无向图,并将其转换为图着色得问题来求解,解释下就是这样得:
1.首先将所有得特征看成图得各个顶点,将不相互独立得特征用一条边连起来,边得权重就是两个相连接得特征得总冲突值(也就是这两个特征上同时不为0得样本个数)。
2.然后按照节点得度对特征降序排序,度越大,说明与其他特征得冲突越大
3.对于每一个特征,遍历已有得特征簇,如果发现该特征加入到特征簇中得矛盾数不超过某一个阈值,则将该特征加入到该簇中。如果该特征不能加入任何一个已有得特征簇,则新建一个簇,将该特征加入到新建得簇中。
具体可以看下面得例子:

上面这个过程得时间复杂度其实是O(#features^2)得,因为要遍历特征,每个特征还要遍历所有得簇,在特征不多得情况下还行,但是如果特征维度很大,就不好使了。所以为了改善效率,可以不建立图,而是将特征按照非零值个数进行排序,因为更多得非零值得特征会导致更多得冲突,所以跳过了上面得第一步,直接排序然后第三步分簇。
对于问题二,捆绑完了之后特征应该如何取值呢?这里面得一个关键就是原始特征能从合并得特征中分离出来,也就是,绑定几个特征在同一个bundle里需要保证绑定前得原始特征得值可以在bundle里面进行识别,考虑到直方图算法将连续得值保存为离散得bins,我们可以是的不同特征得值分到簇中不同bins里面去,这可以通过在特征值中加入一个偏置常数来解决。
比如,我们把特征A和B绑定到了同一个bundle里面,A特征得原始取值区间[0,10),B特征原始取值区间[0,20),这样如果直接绑定,那么会发现我们从bundle里面取出了一个值5,就分不出这个5到底是来自特征A还是B了。所以我们可以再B特征的取值上加一个常数10转换为[10,30),这样绑定好得特征取值就是[0,30),我如果再从bundle里面取出5,就知道这个来自特征A。
从而有趣的是,对于类别特征,如果转换为onehot编码,则这些onehot编码后得多个特征相互之间是互斥得,从而可以被捆绑成为一个特征。因此,对于指定为类别型得特征,lgb可以直接将每个特征取值和一个bin关联,从而自动得处理它们,而需要预处理成onehot编码多此一举。
3.LightGBM得生长策略(leaf-wise)
我们整理了lgb是如何再寻找最优分裂点得过程中降低时间复杂度得,我们说xgb再寻找最优分裂点得时间复杂度其实可以归到三个角度:特征得数量,分裂点得数量和样本得数量。而lgb也提出了三种策略分别从这三个角度进行优化,直方图算法是为了减少分裂点得数量,goss算法为了减少样本得数量,而efb算法为了减少特征得数量。
lgb除了在寻找最优分裂点过程中进行了优化,其实在树得生长过程中也进行了优化,它抛弃了xgb里面得按层生长(level-wise),而是使用了带有深度限制得按叶子生长(leaf-wise)。
xgb在树得生长过程中采用level-wise得增长策略,该策略遍历一次数据可以同时分裂同一层得叶子,容易进行多线程优化,也好控制模型复杂度,不容易过拟合。但实际上level-wise是一种低效得算法,因为它不加区分得对待同一层得叶子,实际上很多叶子得分裂增益较低,没必要进行搜索和分裂,因此带来了很多不必要得计算开销。

leaf-wise则是一种更为高效得策略,每次从当前所有叶子中,找到分裂增益最大得一个叶子,然后分裂,如此循环。因此同level-wise相比,在分裂次数相同得情况下,leaf-wise可以降低更多得误差,得到更好得精度。leaf-wise得缺点是可能会长出比较深得决策树,产生过拟合。因此lgb在leaf-wise之上增加了一个最大深度得限制,在保证高效率得同时防止过拟合。

因此,level-wise得做法会产生一些低信息增益得节点,浪费运算资源,但是这个对防止过拟合挺有用。而leaf-wise能够追求更好得精度,降低误差,但是会带来过拟合问题,其使用了max_depth来控制树得高度防止过拟合,另外直方图和goss得各个操作本身都有天然正则化得作用。
最后还有lgb得工程优化,看下面这个链接:
https://zhongqiang.blog.csdn.net/article/details/105350579
lightGBM - 知乎
在这里提一下lighgbm是第一个直接支持类别特征的GBDT工具。
相关文章:

LightGBM
目录 1.LightGBM的直方图算法(Histogram) 直方图做差加速 2.LightGBM得两大先进技术(GOSS&EFB) 2.1 单边梯度抽样算法(GOSS) 2.2 互斥特征捆绑算法(EFB) 3.LightGBM得生长策略(leaf-wise) 通过与xgboost对比,在这里列出lgb新提出的几个方面的技术 1.Ligh…...
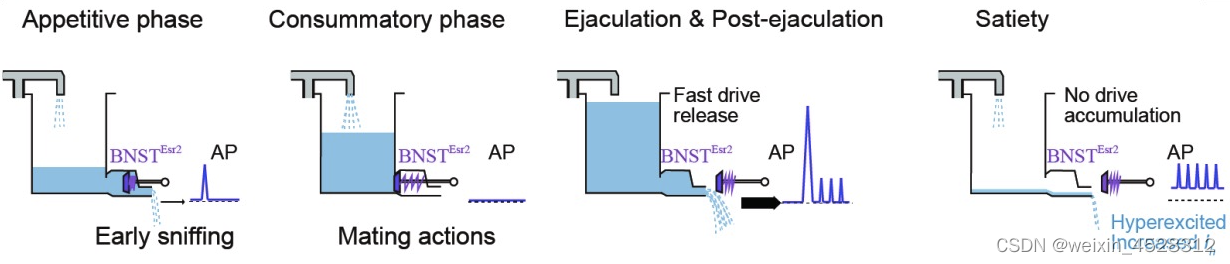
Science:北京脑研究中心李莹实验室揭示性满足感的分子机制
短暂的社交经历(例如,性经历)可导致内部状态的长期变化并影响社会行为,如交配、攻击。例如,在成功交配射精后,许多物种迅速表现出对交配倾向的抑制有数小时、数天或更长时间,这种效应称为性满足…...

Element UI框架学习篇(三)
Element UI框架学习篇(三) 实现简单登录功能(不含记住密码) 1 准备工作 1.1 在zlz包下创建dto包,并创建userDTO类(传输对象) package com.zlz.dto;import lombok.Data;/* DTO 数据传输对象 用户表的传输对象 调用控制器传参使用 VO 控制器返回的视图对象 与页面对应 PO 数据…...
尚硅谷的尚融宝项目
先建立一个Maven springboot项目 进来先把src删掉,因为是一个父项目,我们删掉src之后,pom里配置的东西,也能给别的模块使用。 改一下springboot的版本号码 加入依赖和依赖管理: <properties><java.versi…...

12 Day:内存管理
前言:今天我们要完成我们操作系统的内存管理,以及一些数据结构和小组件的实现,在此之前大家需要了解我们前几天一些重要文件的内存地址存放在哪,以便我们更好的去编写内存管理模块 一,实现ASSERT断言 不知道大家有没有…...

linux基本功系列之lsof命令实战
文章目录前言一. lsof命令介绍二. 语法格式及常用选项三. 参考案例3.1 显示系统打开的文件3.2 查找某个文件相关的进程3.3 列出某个用户打开的文件信息3.4 列出某个程序进程所打开的文件信息3.5 查看某个进程号打开的文件3.6 列出所有的网络连接3.7 列出谁在使用某个端口3.8 恢…...
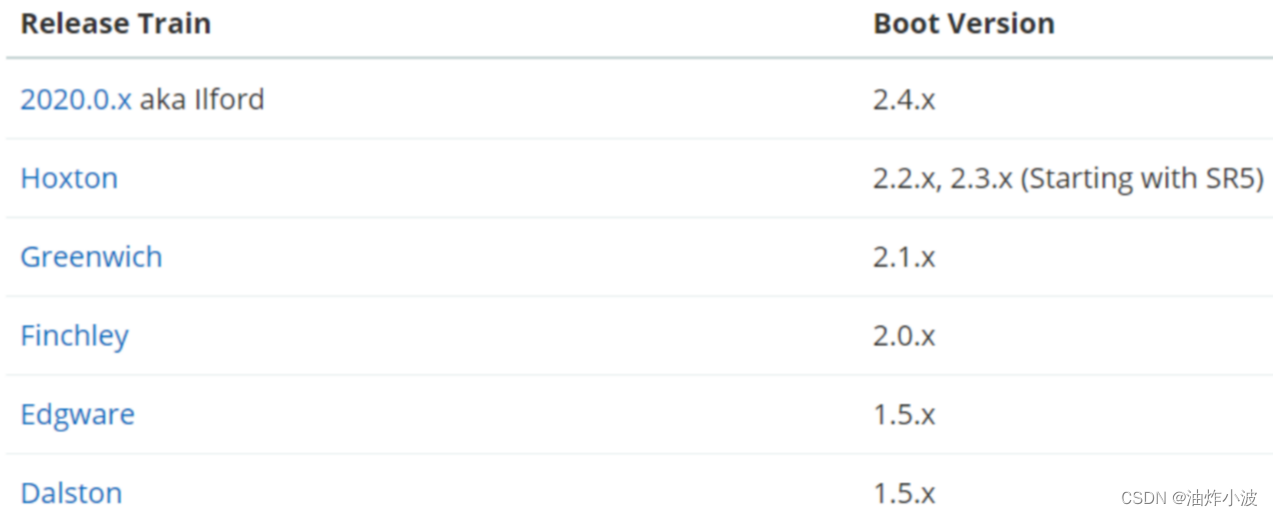
基础篇:02-SpringCloud概述
1.SpringCloud诞生 基于前面章节,我们深知微服务已成为当前开发的主流技术栈,但是如dubbo、zookeeper、nacos、rocketmq、rabbitmq、springboot、redis、es这般众多技术都只解决了一个或一类问题,微服务并没有一个统一的解决方案。开发人员或…...
【软件测试】软件测试工作上95%会遇到的问题,你遇到多少?
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 1、测试负责人要进行…...

4.5.4 LinkedList
文章目录1.特点2.常用方法3.练习:LinkedList测试1.特点 链表,两端效率高,底层就是链表实现的 List接口的实现类,底层的数据结构为链表,内存空间是不连续的 元素有下标,有序允许存放重复的元素在数据量较大的情况下,查询慢&am…...

Python之FileNotFoundError: [Errno 2] No such file or directory问题处理
错误信息:FileNotFoundError: [Errno 2] No such file or directory: ../AutoFrame/temp/report.xlsx相对于当前文件夹的路径,其实就是你写的py文件所在的文件夹路径!python在对文件的操作时,需要特别注意文件地址的书写。文件的路…...

C语言中耳熟能详的printf与scanf
没有什么比时间更有说服力了,因为时间无需通知我们就可以改变一切了。---余华《活着》大家好,今天给大家分享的是C语言中的scanf与printf函数,一提起这两个函数,大家可能觉得这不就是打印和输入嘛?有什么可以说的&…...
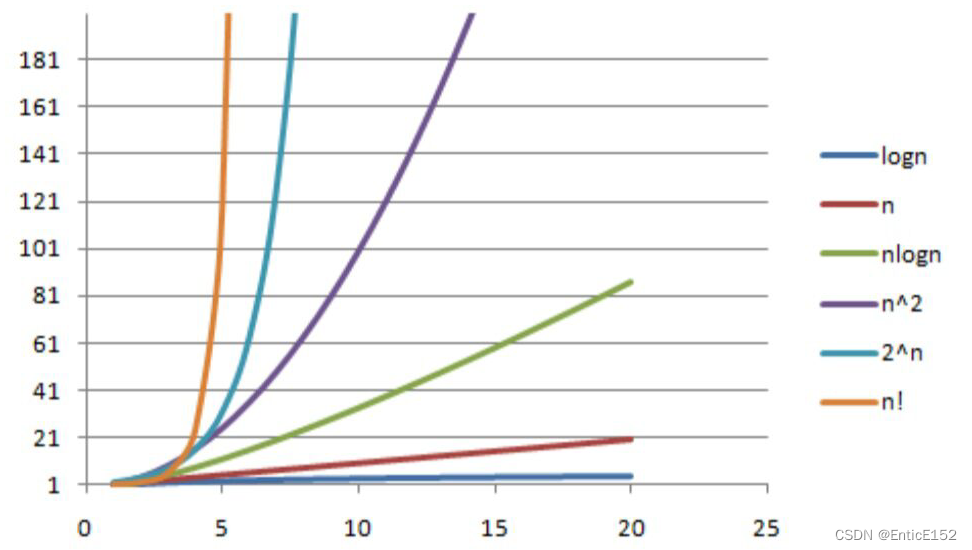
【数据结构】复杂度讲解
目录 时间复杂度与空间复杂度:: 1.算法效率 2.时间复杂度 3.空间复杂度 4.常见时间复杂度以及复杂度OJ练习 时间复杂度与空间复杂度:: 什么是数据结构? 数据结构中是计算机存储,组织数据的方式,指相互之间存在一种或多种特定关…...

JAVA-线程池技术
目录 概念 什么是线程? 什么是线程池? 线程池出现背景 线程池原理图 JAVA提供线程池 线程池参数 如果本篇博客对您有一定的帮助,大家记得留言点赞收藏哦。 概念 什么是线程? 是操作系统能够进行运算调度的最小单位。&am…...
)
【C++】从0到1入门C++编程学习笔记 - 提高编程篇:STL常用算法(算术生成算法)
文章目录一、accumulate二、fill学习目标: 掌握常用的算术生成算法 注意: 算术生成算法属于小型算法,使用时包含的头文件为 #include <numeric> 算法简介: accumulate // 计算容器元素累计总和 fill // 向容器中添加元…...

【C++】static成员
💙作者:阿润菜菜 📖专栏:C 目录 概念 特性 出个题 概念 声明为static的类成员称为类的静态成员,用static修饰的成员变量,称之为静态成员变量; 用static修饰的成员函数,称之为静态…...
Python Scrapy 爬虫简单教程
1. Scrapy install 准备知识 pip 包管理Python 安装XpathCssWindows安装 Scrapy $>- pip install scrapy Linux安装 Scrapy $>- apt-get install python-scrapy 2. Scrapy 项目创建 在开始爬取之前,必须创建一个新的Scrapy项目。进入自定义的项目目录中&am…...
【DOCKER】容器概念基础
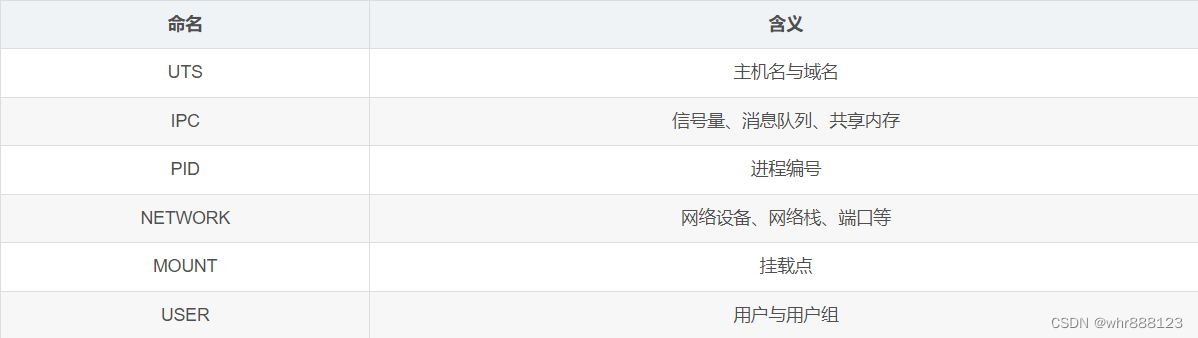
文章目录1.容器1.概念2.特点3.与虚拟机的对比2.docker1.概念2.命名空间3.核心概念3.命令1.镜像命令2.仓库命令1.容器 1.概念 1.不同的运行环境,底层架构是不同的,这就会导致测试环境运行好好的应用,到了生产环境就会出现bug(就像…...
第九层(16):STL终章——常用集合算法
文章目录前情回顾常用集合算法set_intersectionset_unionset_difference最后一座石碑倒下,爬塔结束一点废话🎉welcome🎉 ✒️博主介绍:一名大一的智能制造专业学生,在学习C/C的路上会越走越远,后面不定期更…...

一起学习用Verilog在FPGA上实现CNN----(六)SoftMax层设计
1 SoftMax层设计 1.1 softmax SoftMax函数的作用是输入归一化,计算各种类的概率,即计算0-9数字的概率,SoftMax层的原理图如图所示,输入和输出均为32位宽的10个分类,即32x10320 本项目softmax实现逻辑为: …...

pixhawk2.4.8-APM固件-MP地面站配置过程记录
目录一、硬件准备二、APM固件、MP地面站下载三、地面站配置1 刷固件2 机架选择3 加速度计校准4 指南针校准5 遥控器校准6 飞行模式7 紧急断电&无头模式8 基础参数设置9 电流计校准10 电调校准11 起飞前检查(每一项都非常重要)12 飞行经验四、遇到的问…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

【Zephyr 系列 16】构建 BLE + LoRa 协同通信系统:网关转发与混合调度实战
🧠关键词:Zephyr、BLE、LoRa、混合通信、事件驱动、网关中继、低功耗调度 📌面向读者:希望将 BLE 和 LoRa 结合应用于资产追踪、环境监测、远程数据采集等场景的开发者 📊篇幅预计:5300+ 字 🧭 背景与需求 在许多 IoT 项目中,单一通信方式往往难以兼顾近场数据采集…...

湖北理元理律师事务所:债务清偿方案中的法律技术革新
文/金融法律研究组 当前债务服务市场存在结构性矛盾:债权人追求快速回款,债务人需要喘息空间。湖北理元理律师事务所通过创新法律技术,在《企业破产法》《民法典》框架下构建梯度清偿模型,实现多方利益平衡。 一、个人债务优化的…...

SpringSecurity+vue通用权限系统
SpringSecurityvue通用权限系统 采用主流的技术栈实现,Mysql数据库,SpringBoot2Mybatis Plus后端,redis缓存,安全框架 SpringSecurity ,Vue3.2Element Plus实现后台管理。基于JWT技术实现前后端分离。项目开发同时采 …...

【计算机网络】SDN
SDN这种新型网络体系结构的核心思想:把网络的控制层面与数据层面分离,而让控制层面利用软件来控制数据层面中的许多设备。 OpenFlow协议可以被看成是SDN体系结构中控制层面与数据层面之间的通信接口。 在SDN中取代传统路由器中转发表的是“流表”&…...
