信息熵 条件熵 交叉熵 联合熵 相对熵(KL散度) 互信息(信息增益)
粗略版快速总结
条件熵 H ( Q ∣ P ) = 联合熵 H ( P , Q ) − H ( P ) 条件熵H(Q∣P)=联合熵H(P,Q)−H(P) 条件熵H(Q∣P)=联合熵H(P,Q)−H(P)
信息增益 I ( P , Q ) = H ( P ) − H ( P ∣ Q ) = H ( P ) + H ( Q ) − H ( P , Q ) 信息增益 I(P,Q)=H(P)−H(P∣Q)=H(P)+H(Q)-H(P,Q) 信息增益I(P,Q)=H(P)−H(P∣Q)=H(P)+H(Q)−H(P,Q),也就是Information Gain,互信息
KL散度(相对熵) K L ( P , Q ) = − H ( P ) + 交叉熵 C E ( P , Q ) KL(P,Q)=-H(P)+交叉熵CE(P,Q) KL(P,Q)=−H(P)+交叉熵CE(P,Q)
详细定义
如果一个样本是n类其中之一,也就是说target是onehot形式,例如三类那么target=[0,0,1],拿target=[0,0,1]来说就是 p 0 = 0 p_0=0 p0=0, p 1 = 0 p_1=0 p1=0, p 2 = 1 p_2=1 p2=1。写成表达式可以是 p i p_i pi,n=3
那么经过神经网络运算出来的Logits可能是在(-inf,inf)之间,那么一般会通过softmax归一化到(0,1)之间,这个归一化到(0,1)之间的数我们可以用 q i q_i qi来表示,当然对于上面有3类的例子来说,n=3
好了,既然明确了 p i p_i pi是第i个类的在(0,1)之间target, q i q_i qi是第i个类的logit归一化到(0,1)之间的结果,那么开始各种定义了
相对熵(KL散度)
K L ( P , Q ) = ∑ i ∈ [ 0 , n − 1 ] p i l o g p i q i KL(P,Q)=\sum _{i \in[0,n-1]}p_i log \frac{p_i}{q_i} KL(P,Q)=i∈[0,n−1]∑pilogqipi
交叉熵(CE Loss)
C E ( P , Q ) = − ∑ i ∈ [ 0 , n − 1 ] p i l o g q i K L ( P , Q ) = H ( P ) + C E ( P , Q ) CE(P,Q)=-\sum _{i \in[0,n-1]}p_i log q_i \\ KL(P,Q) = H(P)+CE(P,Q) CE(P,Q)=−i∈[0,n−1]∑pilogqiKL(P,Q)=H(P)+CE(P,Q)
来看一下Pytorch里的交叉熵是怎么实现的,手动验证下:
import torch
from torch import nn
import mathloss_f = nn.CrossEntropyLoss(reduction='mean')
output = torch.randn(2,3) #表示2个样本,3个类别
# target = torch.from_numpy(np.array([1, 0])).type(torch.LongTensor)
target = torch.LongTensor([0,2]) #表示label0和label2
loss = loss_f(output, target)print('CrossEntropy loss: ', loss)
print(f'reduction=none,所以可以看到每一个样本loss,输出为[{loss}]')def manual_cal(sample_index, target, output):#输入是样本下标sample_output = output[sample_index]sample_target = target[sample_index]x_class = sample_output[sample_target]sample_output_len = len(sample_output)log_sigma_exp_x = math.log(sum(math.exp(sample_output[i]) for i in range(sample_output_len)))sample_loss = -x_class + log_sigma_exp_xprint(f'交叉熵手动计算loss{sample_index}:{sample_loss}')return sample_lossfor i in range(2):manual_cal(i, target, output)# 如果nn.CrossEntropyLoss(reduction='mean')模式,刚好是手动计算的每个样本的loss取平均,最后输出的是一个值
# 如果nn.CrossEntropyLoss(reduction='none')模式,手动计算的loss0和loss1都会被列出来

(class torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction=‘elementwise_mean’)
功能: 将输入经过softmax激活函数之后,再计算其与target的交叉熵损失。即该方法将nn.LogSoftmax()和 nn.NLLLoss()进行了结合。严格意义上的交叉熵损失函数应该是nn.NLLLoss()。

补充:交叉熵损失(cross-entropy Loss) 又称为对数似然损失(Log-likelihood Loss)、对数损失;二分类时还可称之为逻辑斯谛回归损失(Logistic Loss)。交叉熵损失函数表达式为 L = - sigama(y_i * log(x_i))。pytroch这里不是严格意义上的交叉熵损失函数(下面会详细解释,pytorch中交叉熵不够严格主要是因为只能接受one hot),而是先将input经过softmax激活函数,将向量“归一化”成概率形式,然后再与target计算严格意义上交叉熵损失。 在多分类任务中,经常采用softmax激活函数+交叉熵损失函数,因为交叉熵描述了两个概率分布的差异,然而神经网络输出的是向量,并不是概率分布的形式。所以需要softmax激活函数将一个向量进行“归一化”成概率分布的形式,再采用交叉熵损失函数计算loss。 再回顾PyTorch的CrossEntropyLoss(),官方文档中提到时将nn.LogSoftmax()和 nn.NLLLoss()进行了结合,nn.LogSoftmax() 相当于激活函数 , nn.NLLLoss()是损失函数;
来感受一下交叉熵取值的妙处:当 q i q_i qi很接近1时, − l o g q i -logq_i −logqi很接近0,如果此时 p i p_i pi是1,这时候整体loss会很小;当 q i q_i qi很接近0时, − l o g q i -logq_i −logqi很大, p i p_i pi是1,这时候整体loss会很大。所以 p i p_i pi就是筛选的功能,在Pytorch中CrossEntropyLoss等于LogSoftmax和NLLLoss的结合:LogSoftmax是上面公式里的 l o g ( e x p ( x [ c l a s s ] ) ∑ j e x p ( x [ j ] ) ) log(\frac{exp(x[class])}{\sum_jexp(x[j])}) log(∑jexp(x[j])exp(x[class])),实现了整个 l o g q i logq_i logqi的效果;NLLLoss就是给前面加了一个负号。所以在torch中的CrossEntropy = NLLLoss(LogSoftmax)
pytorch中交叉熵不够严格主要是因为只能接受one hot,也就是说torch中的target只能明确指明是哪个target,而不是上面公式 p i p_i pi是(0,1)之间,所以在Pytorch中还保留了KLDivLoss这个loss来接受广泛的取值:
import torch.nn.functional as F
import torch
import torch.nn as nn
# nn.CrossEntropyLoss() 和 KLDivLoss 关系y_pred = torch.tensor([[10.0, 0.0, -10.0], [8.0, 8.0, 8.0]])
y_true = torch.tensor([0, 2])
ce = nn.CrossEntropyLoss(reduction="none")(y_pred, y_true)
print(ce)
'''
输出shape是2,tensor([4.5418e-05, 1.0986e+00])
'''# NLLLoss要求target只能是第几类下标,例如[0,2]表示[label0,label2],转成onehot就是[[1,0,0],[0,0,1]]
nll_log_softmax = nn.NLLLoss(reduction="none")(F.log_softmax(y_pred, dim=-1), y_true)
print(nll_log_softmax)
'''
输出shape是2,tensor([4.5418e-05, 1.0986e+00])
'''one_hot = F.one_hot(y_true) #将第几类的下标转换成onehot形式,例如输入[0,2]表示[label0,label2],输出onehot就是[[1,0,0],[0,0,1]]
'''
# KLDivLoss要求target为float形式编码,one_hot是longtensor,所以要one_hot.float();如果是普通的logics,要过一下softmax# KLDivLoss也要求Logits经过LogSoftmax激活。LogSoftmax会把(-inf,inf)的Logits映射到(0,1)再映射到(-inf,0):当用NLLLoss时,刚好多个负号loss变成(0,inf);当用KLDivLoss时,刚好多个熵。回顾klLoss的公式 p_i*log(p_i/q_i),其中p_i是(0,1)范围内的targets
q_i是将logits映射到(0,1)范围内的结果,所以p_i和q_i都是(0,1)之间
KLDivLoss这个函数的特点就是把log(q_i)这一步扔给输入自己算,这个函数管的只是p_i*log(p_i)-p_i*inputNLLLoss这个函数的特点就是把p_i*log(p_i)也没了,只有-p_i*input,所以和LogSoftmax组合起来是CE
'''kl = nn.KLDivLoss(reduction="none")(F.log_softmax(y_pred, dim=-1), one_hot.float())
print(kl) #输出shape是2*3
'''
tensor([[4.5418e-05, 0.0000e+00, 0.0000e+00],[0.0000e+00, 0.0000e+00, 1.0986e+00]])
'''a = F.softmax(torch.randn(2,3))
print(nn.KLDivLoss(reduction="none")(torch.log(a), a))
'''
输出是
tensor([[0., 0., 0.],[0., 0., 0.]])回顾klLoss的公式 p_i*log(p_i/q_i),其中p_i是(0,1)范围内的targets
q_i是将logits映射到(0,1)范围内的结果,所以p_i和q_i都是(0,1)之间
KLDivLoss这个函数的特点就是把log(q_i)这一步扔给输入自己算,这个函数管的只是p_i*log(p_i)-p_i*inputNLLLoss这个函数的特点就是把p_i*log(p_i)也没了,只有-p_i*input,所以和LogSoftmax组合起来是CE
'''
为什么既有 KL 散度又有交叉熵?在信息论中,熵的意义是对 𝑃
事件的随机变量编码所需的最小字节数,KL 散度的意义是**“额外所需的编码长度”如果我们使用 𝑄的编码来表示 𝑃**,交叉熵指的是当你使用 𝑄作为密码来表示 𝑃 是所需要的 “平均的编码长度”。但是在机器学习评价两个分布之间的差异时,由于分布 𝑃 会是给定的,所以此时 KL 散度和交叉熵的作用其实是一样的,而且因为交叉熵少算一项,更加简单,所以选择交叉熵会更好。
Label Smoothing
Label Smoothing是一种防止网络过拟合的手段,在Pytorch的CrossEntropy中已经自带了这个参数,下图截自Hinton的论文When Does Label Smoothing Help? 从公式来看只把我们上面说的label/target做了一个衰减,更多细节可以参考https://blog.csdn.net/taoqick/article/details/121717218 :

联合熵
H ( P , Q ) = − ∑ i ∈ [ 0 , n − 1 ] P ( p i , q i ) l o g P ( p i , q i ) H(P,Q)=-\sum _{i \in[0,n-1]}P(p_i,q_i)logP(p_i,q_i) H(P,Q)=−i∈[0,n−1]∑P(pi,qi)logP(pi,qi)
条件熵
注意下面 P ( q i ∣ p i ) P(q_i|p_i) P(qi∣pi)表示 p i p_i pi和 q i q_i qi对应变量的条件概率, P ( p i , q i ) P(p_i,q_i) P(pi,qi)表示 p i p_i pi和 q i q_i qi对应变量的联合概率,写成这样只是为了简化但不够严谨。
H ( Q ∣ P ) = ∑ i ∈ [ 0 , n − 1 ] p i H ( Q ∣ P = p i ) H ( Q ∣ P ) = − ∑ i ∈ [ 0 , n − 1 ] p i ∗ P ( q i ∣ p i ) l o g P ( q i ∣ p i ) H ( Q ∣ P ) = − ∑ i ∈ [ 0 , n − 1 ] P ( p i , q i ) l o g P ( q i ∣ p i ) H(Q|P)=\sum _{i \in[0,n-1]}p_iH(Q|P=p_i) \\ H(Q|P)=-\sum _{i \in[0,n-1]}p_i*P(q_i|p_i)logP(q_i|p_i) \\ H(Q|P)=-\sum _{i \in[0,n-1]}P(p_i,q_i)logP(q_i|p_i) H(Q∣P)=i∈[0,n−1]∑piH(Q∣P=pi)H(Q∣P)=−i∈[0,n−1]∑pi∗P(qi∣pi)logP(qi∣pi)H(Q∣P)=−i∈[0,n−1]∑P(pi,qi)logP(qi∣pi)
上面就解释了为啥log里面是条件,外面是联合,更进一步地把里面也展开
H ( Q ∣ P ) = − ∑ i ∈ [ 0 , n − 1 ] P ( p i , q i ) l o g P ( q i ∣ p i ) H ( Q ∣ P ) = − H ( P , Q ) − ∑ i ∈ [ 0 , n − 1 ] P ( p i , q i ) l o g P ( p i ) H ( Q ∣ P ) = − H ( P , Q ) + H ( P ) H(Q|P)=-\sum _{i \in[0,n-1]}P(p_i,q_i)logP(q_i|p_i) \\ H(Q|P)=-H(P,Q)-\sum _{i \in[0,n-1]}P(p_i,q_i)logP(p_i) \\ H(Q|P)=-H(P,Q)+H(P) H(Q∣P)=−i∈[0,n−1]∑P(pi,qi)logP(qi∣pi)H(Q∣P)=−H(P,Q)−i∈[0,n−1]∑P(pi,qi)logP(pi)H(Q∣P)=−H(P,Q)+H(P)
至于熵为什么是这个定义请参考 为什么信息熵要定义成 − Σ p ∗ l o g ( p ) -Σp*log(p) −Σp∗log(p)?(https://blog.csdn.net/taoqick/article/details/72852255)。简单来说就是-log§就是信息量,单位用比特表示,例如中国队夺世界杯的信息量远比法国队夺世界杯信息量大。把一个系统里所有的-log§再乘以p就是熵,表示所有信息量加权平均,或者说熵就是信息量的数学期望
还有3个重要结论:
-
最小化交叉熵和极大似然本质上是一样的,更多推导参考:最小化交叉熵损失与极大似然 - 知乎(https://zhuanlan.zhihu.com/p/51099880)
-
为什么分类问题用相对熵不用MSE,原因之一是求解时相对熵的梯度下降更快一些,这样可以实现错误越大,下降的越快的效果,更多推导请参考: 分类问题中为什么用交叉熵而不用MSE KL散度和交叉熵的关系_taoqick的专栏-CSDN博客_mse和交叉熵 (https://blog.csdn.net/taoqick/article/details/102621605)
-
李航老师书里说的最大熵模型是条件熵最大化,想法就是某些知识已经先验知道了,剩下的随机变量尽量等概率随机,这样条件熵最大。学习概率模型时,在满足约束(特征函数)的所有的可能的概率分布中,熵最大的模型就是最大的模型。最大熵模型是判别式模型。
更多推导请参考李航老师的书和数学之美。
相关文章:

信息熵 条件熵 交叉熵 联合熵 相对熵(KL散度) 互信息(信息增益)
粗略版快速总结 条件熵 H ( Q ∣ P ) 联合熵 H ( P , Q ) − H ( P ) 条件熵H(Q∣P)联合熵H(P,Q)−H(P) 条件熵H(Q∣P)联合熵H(P,Q)−H(P) 信息增益 I ( P , Q ) H ( P ) − H ( P ∣ Q ) H ( P ) H ( Q ) − H ( P , Q ) 信息增益 I(P,Q)H(P)−H(P∣Q)H(P)H(Q)-H(P,Q) 信息…...

Fiddler Response私人订制
在客户端接口的测试中,我们经常会需要模拟各种返回状态或者特定的返回值,常见的是用Fiddler模拟各种请求返回值场景,如重定向AutoResponder、请求拦截修改再下发等等。小编在近期的测试中遇到的一些特殊的请求返回模拟的测试场景,…...
【德哥说库系列】-ASM管理Oracle 19C单实例部署
📢📢📢📣📣📣 哈喽!大家好,我是【IT邦德】,江湖人称jeames007,10余年DBA及大数据工作经验 一位上进心十足的【大数据领域博主】!😜&am…...
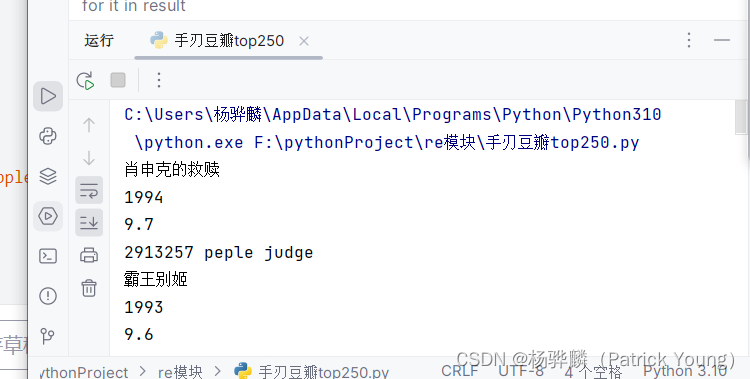
手写一个简单爬虫--手刃豆瓣top250排行榜
#拿到页面面源代码 request #通过re来提取想要的有效信息 re import requests import re url"https://movie.douban.com/top250"headers{"user-agent":"Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/11…...
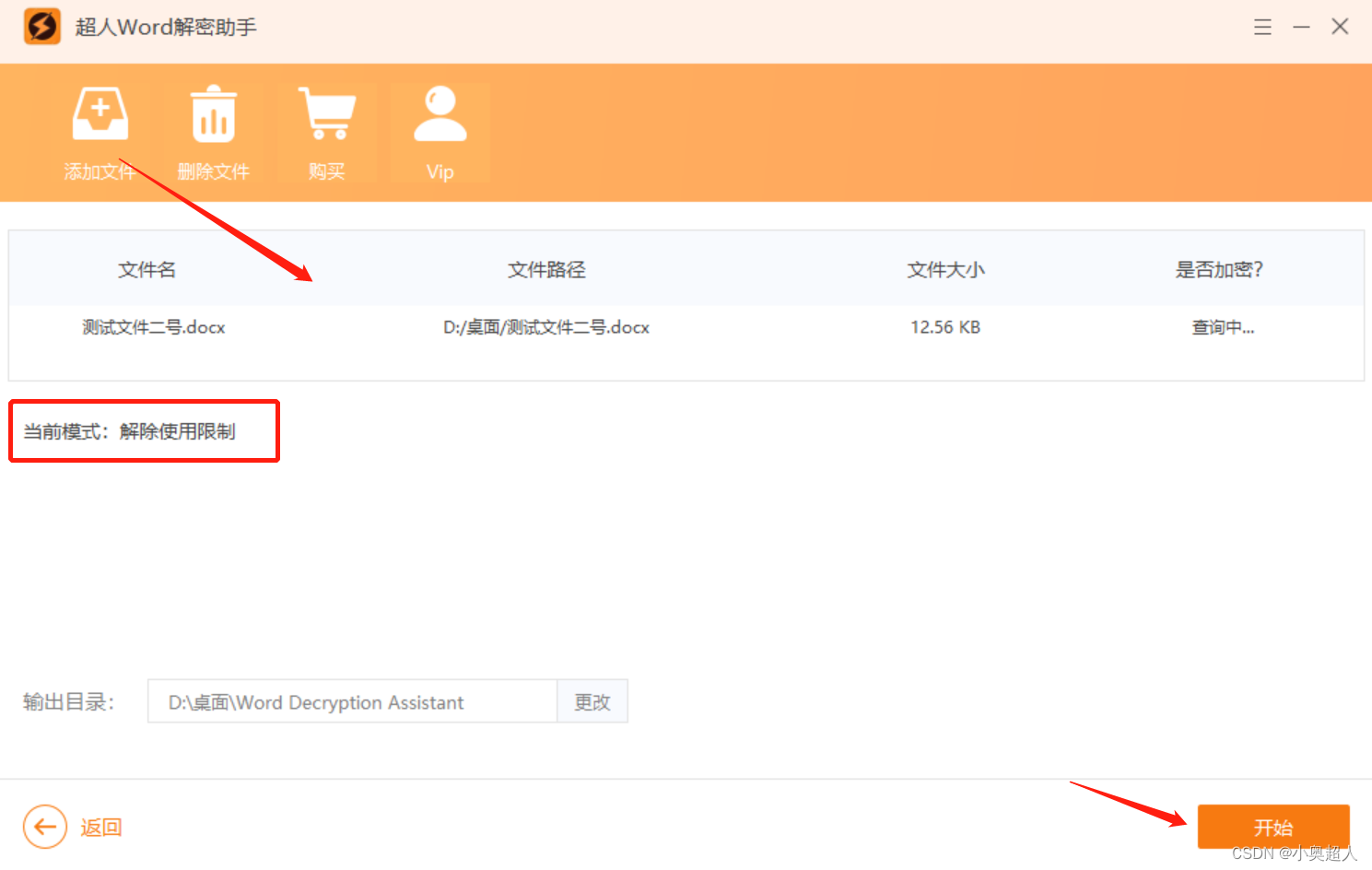
【word密码】如何限制word文件中部分内容?
Word文件中有一部分内容不想他人编辑,我们可以设置限制编辑,可以对一部分内容设置限制编辑,具体方法如下: 我们将需要将可以编辑的地方选中,然后打开限制编辑功能 然后勾选限制编辑设置界面中的【限制编辑】和【每个人…...

spring 自定义类型转换-ConverterRegistry
1背景介绍 一个应用工程里面,一遍会涉及到很多的模型转换,如DTO模型转DO模型,DO模型转DTO, 或者Request转DTO模型,总的来说,维护起来还是相对比较复杂。每涉及一个转换都需要重新写对应类的get或者set方法,…...

springboot实现发送短信验证码
目录 一、选择并注册短信服务提供商: 二、添加依赖: 三、配置短信服务信息: 四、编写发送短信验证码的方法: 五、调用发送短信验证码的方法: 一、选择并注册短信服务提供商: 1、选择一个可靠的短信服…...

2024王道408数据结构P144 T18
2024王道408数据结构P144 T18 思考过程 首先还是先看题目的意思,让我们在中序线索二叉树里查找指定结点在后序的前驱结点,这题有一点难至少对我来说…我讲的不清楚理解一下我做的也有点糊涂。在创建结构体时多两个变量ltag和rtag,当ltag0时…...

在windows下安装配置skywalking
1.下载地址 Downloads | Apache SkyWalkinghttp://skywalking.apache.org/downloads/ 2.文件目录说明 将文件解压后,可看到agent和bin目录: Agent:作为探针,安装在服务器端,进行数据采集和上报。 Config:…...
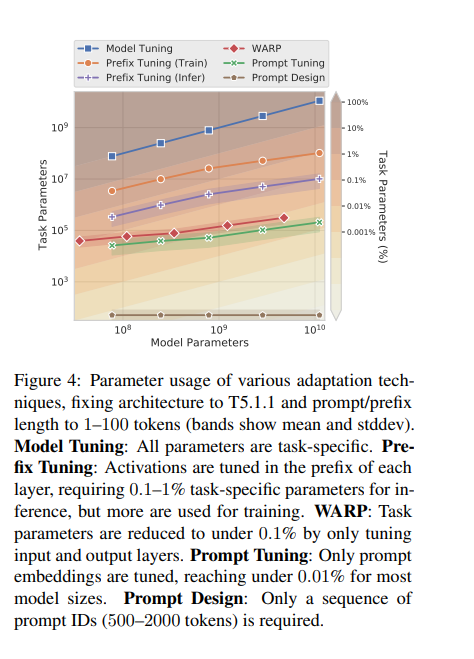
关于大模型参数微调的不同方法
Adapter Tuning 适配器模块(Adapter Moudle)可以生成一个紧凑且可扩展的模型;每个任务只需要添加少量可训练参数,并且可以在不重新访问之前任务的情况下添加新任务。原始网络的参数保持不变,实现了高度的参数共享 Pa…...
)
方法的引用第一版(method reference)
1、体验方法引用 在使用Lambda表达式的时候,我们实际上传递进去的代码就是一种解决方案:拿参数做操作那么考虑一种情况:如果我们在Lanbda中所指定的操作方案,已经有地方存在相同方案,那是否还有必要再重复逻辑呢&#…...

Android DataBinding 基础入门(学习记录)
目录 一、DataBinding简介二、findViewById 和 DataBinding 原理及优缺点1. findViewById的优缺点2. DataBinding的优缺点 三、Android mvvm 之 databinding 原理1. 简介和三个主要的实体DataViewViewDataBinding 2.三个功能2.1. rebind 行为2.2 observe data 行为2.3 observe …...

spring 错误百科
一、使用Spring出错根源 1、隐式规则的存在 你可能忽略了 Sping Boot 中 SpringBootApplication 是有一个默认的扫描包范围的。这就是一个隐私规则。如果你原本不知道,那么犯错概率还是很高的。类似的案例这里不再赘述。 2、默认配置不合理 3、追求奇技淫巧 4、…...
OpenCV基本操(IO操作,读取、显示、保存)
图像的IO操作,读取和保存方法 1.1 API cv.imread()参数: 要读取的图像 读取图像的方式: cv.IMREAD*COLOR:以彩色模式加载图像,任何图像的图像的透明度都将被忽略。这是默认参数 标志: 1 cv.IMREAD*GRAYSCALE :以…...

1.快速搭建Flask项目
一.Pear Admin Flask 官网文档:http://www.pearadmin.com/doc/index.html 1.1下载安装 # 下 载 git clone https://gitee.com/pear-admin/pear-admin-flask# 安 装 pip install -r requirements.txt1.2修改配置 applications下的config.py docker运行的修改dockerdata/conf…...

编程题四大算法思想(三)——贪心法:找零问题、背包问题、任务调度问题、活动选择问题、Prim算法
文章目录 贪心法找零问题(change-making problem)贪心算法要求基本思想适合求解问题的特征 背包问题0/1背包问题0/1背包问题——贪心法 分数背包问题 任务调度问题活动选择问题活动选择——贪心法最早结束时间优先——最优性证明 Prim算法 贪心法 我在当…...
core dump管理在linux中的前世今生
目录 一、什么是core dump? 二、coredump是怎么来的? 三、怎么限制coredump文件的产生? ulimit 半永久限制 永久限制 四、从源码分析如何对coredump文件的名字和路径管理 命名 管理 一些问题的答案 1、为什么新的ubuntu不能产生c…...

Springboot整合knife4j配置swagger教程-干货
开启swagger文档,直接上教程。 第一步:引入依赖 <!--swagger 依赖--><dependency><groupId>com.github.xiaoymin</groupId><artifactId>knife4j-spring-boot-starter</artifactId><version>3.0.3</version></d…...

C++ 中的 Pimpl 惯用法
C 中的 Pimpl 惯用法 介绍 Pimpl(Pointer to Implementation)是一种常见的 C 设计模式,用于隐藏类的实现细节,从而减少编译依赖和提高编译速度。本文将通过一个较为复杂的例子,展示如何使用智能指针(如 s…...

【个人博客系统网站】统一处理 · 拦截器
【JavaEE】进阶 个人博客系统(2) 文章目录 【JavaEE】进阶 个人博客系统(2)1. 统一返回格式处理1.1 统一返回类common.CommonResult1.2 统一返回处理器component.ResponseAdvice 2. 统一异常处理3. 拦截器实现3.1 全局变量SESSI…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...

嵌入式面试常问问题
以下内容面向嵌入式/系统方向的初学者与面试备考者,全面梳理了以下几大板块,并在每个板块末尾列出常见的面试问答思路,帮助你既能夯实基础,又能应对面试挑战。 一、TCP/IP 协议 1.1 TCP/IP 五层模型概述 链路层(Link Layer) 包括网卡驱动、以太网、Wi‑Fi、PPP 等。负责…...
