多传感器融合定位十四-基于图优化的定位方法
多传感器融合定位十四-基于图优化的定位方法
- 1. 基于图优化的定位简介
- 1.1 核心思路
- 1.2 定位流程
- 2. 边缘化原理及应用
- 2.1 边缘化原理
- 2.2 从滤波角度理解边缘化
- 3. 基于kitti的实现原理
- 3.1 基于地图定位的滑动窗口模型
- 3.2 边缘化过程
- 4. lio-mapping 介绍
- 4.1 核心思想
- 4.2 具体流程
- 4.2.1 各类因子
- 4.2.2 滑窗模型
- 4.2.3 边缘化
- 4.2.4 添加新帧
Reference:
- 深蓝学院-多传感器融合
- 多传感器融合定位理论基础
文章跳转:
- 多传感器融合定位一-3D激光里程计其一:ICP
- 多传感器融合定位二-3D激光里程计其二:NDT
- 多传感器融合定位三-3D激光里程计其三:点云畸变补偿
- 多传感器融合定位四-3D激光里程计其四:点云线面特征提取
- 多传感器融合定位五-点云地图构建及定位
- 多传感器融合定位六-惯性导航原理及误差分析
- 多传感器融合定位七-惯性导航解算及误差分析其一
- 多传感器融合定位八-惯性导航解算及误差分析其二
- 多传感器融合定位九-基于滤波的融合方法Ⅰ其一
- 多传感器融合定位十-基于滤波的融合方法Ⅰ其二
- 多传感器融合定位十一-基于滤波的融合方法Ⅱ
- 多传感器融合定位十二-基于图优化的建图方法其一
- 多传感器融合定位十三-基于图优化的建图方法其二
- 多传感器融合定位十四-基于图优化的定位方法
- 多传感器融合定位十五-多传感器时空标定(综述)
1. 基于图优化的定位简介
1.1 核心思路
核心思路是把融合方法从滤波换成图优化,其元素不再是简单的惯性解算,而是预积分。
一个暴力的模型可以设计为:
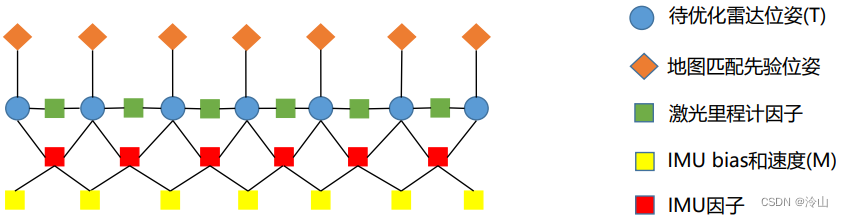
缺陷:随着时间的进行,图模型会越来越大,导致无法达到实时性。
解决方法:不断删除旧的帧,只优化最新的几帧,即维持一个滑动窗口。
模型如下:
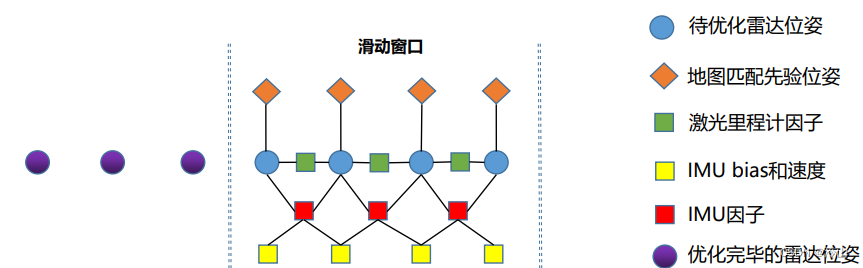
问题:直接从模型中删除,等于损失了信息。
解法:通过模型把旧帧的约束传递下来,即边缘化(后面讲具体细节)。
1.2 定位流程

整个流程:不断往滑窗里添加新信息,并边缘化旧信息。
需要注意的是:
- 正常行驶时,不必像建图那样,提取稀疏的关键帧;
- 停车时,需要按一定策略提取关键帧,但删除的是次新帧,因此不需要边缘化。
2. 边缘化原理及应用
2.1 边缘化原理
优化问题具有如下通用形式:
HX=bH X=b HX=b并可拆解成如下形式:
[HmmHmrHrmHrr][XmXr]=[bmbr]\left[\begin{array}{cc} H_{m m} & H_{m r} \\ H_{r m} & H_{r r} \end{array}\right]\left[\begin{array}{c} X_m \\ X_r \end{array}\right]=\left[\begin{array}{l} b_m \\ b_r \end{array}\right] [HmmHrmHmrHrr][XmXr]=[bmbr]拆解的目的是通过一系列操作,把 XmX_mXm 从状态量 里删除掉,并把它的约束保留下来。
在滑窗模式里,这个 XmX_mXm 即为要边缘化掉的量。
回顾舒尔补:
给定矩阵
M=[ABCD]M=\left[\begin{array}{ll} \mathrm{A} & \mathrm{B} \\ \mathrm{C} & \mathrm{D} \end{array}\right] M=[ACBD]它可以通过如下变换,变成上三角矩阵,即
[I0−CA−1I][ABCD]=[AB0ΔA]\left[\begin{array}{cc} \mathrm{I} & 0 \\ -\mathrm{CA}^{-1} & \mathrm{I} \end{array}\right]\left[\begin{array}{cc} \mathrm{A} & \mathrm{B} \\ \mathrm{C} & \mathrm{D} \end{array}\right]=\left[\begin{array}{cc} \mathrm{A} & \mathrm{B} \\ 0 & \Delta \mathrm{A} \end{array}\right] [I−CA−10I][ACBD]=[A0BΔA]其中, ΔA=D−CA−1B\Delta \mathrm{A}=\mathrm{D}-\mathrm{CA}^{-1} \mathrm{~B}ΔA=D−CA−1 B 称为 A\mathrm{A}A 关于 M\mathrm{M}M 的舒尔补。
拆解后的优化问题,可通过舒尔补对矩阵三角化, 即
[I0−HrmHmm−1I][HmmHmrHrmHrr][XmXr]=[I0−HrmHmm−1I][bmbr]\begin{aligned} & {\left[\begin{array}{cc} I & 0 \\ -H_{r m} H_{m m}^{-1} & I \end{array}\right]\left[\begin{array}{cc} H_{m m} & H_{m r} \\ H_{r m} & H_{r r} \end{array}\right]\left[\begin{array}{c} X_m \\ X_r \end{array}\right] } \\ = & {\left[\begin{array}{cc} I & 0 \\ -H_{r m} H_{m m}^{-1} & I \end{array}\right]\left[\begin{array}{l} b_m \\ b_r \end{array}\right] } \end{aligned} =[I−HrmHmm−10I][HmmHrmHmrHrr][XmXr][I−HrmHmm−10I][bmbr]
进一步化简得,
[HmmHmr0Hrr−HrmHmm−1Hmr][XmXr]=[bmbr−HrmHmm−1bm]\begin{aligned} & {\left[\begin{array}{cc} H_{m m} & H_{m r} \\ 0 & H_{r r}-H_{r m} H_{m m}^{-1} H_{m r} \end{array}\right]\left[\begin{array}{c} X_m \\ X_r \end{array}\right] } \\ = & {\left[\begin{array}{c} b_m \\ b_r-H_{r m} H_{m m}^{-1} b_m \end{array}\right] } \end{aligned} =[Hmm0HmrHrr−HrmHmm−1Hmr][XmXr][bmbr−HrmHmm−1bm]此时,可以利用等式第2行直接得到:
(Hrr−HrmHmm−1Hmr)Xr=br−HrmHmm−1bm\left(H_{r r}-H_{r m} H_{m m}^{-1} H_{m r}\right) X_r=b_r-H_{r m} H_{m m}^{-1} b_m (Hrr−HrmHmm−1Hmr)Xr=br−HrmHmm−1bm
其含义为:此时可以不依赖 XmX_mXm 求解出 XrX_rXr,若我们只关心 XrX_rXr 的值,则可以把 XmX_mXm 从模型里删除。
2.2 从滤波角度理解边缘化
kalman滤波是此前已经熟悉的,从边缘化的 角度重新看一遍滤波器的推导,更有利于深入 理解。
运动模型与观测模型分别为:
xk=Ak−1xk−1+vk+wkyk=Ckxk+nk\begin{aligned} & \mathbf{x}_k=\mathbf{A}_{k-1} \mathbf{x}_{k-1}+\mathbf{v}_k+\mathbf{w}_k \\ & \mathbf{y}_k=\mathbf{C}_k \mathbf{x}_k+\mathbf{n}_k \end{aligned} xk=Ak−1xk−1+vk+wkyk=Ckxk+nk
其中 k=1…Kk=1 \ldots Kk=1…K状态量的求解,可以等效为如下模型
x^=argminxJ(x)\hat{\mathbf{x}}=\arg \min _{\mathbf{x}} J(\mathbf{x}) x^=argxminJ(x)
其中
J(x)=∑k=0K(Jv,k(x)+Jy,k(x))Jv,k(x)={12(x0−xˇ0)TPˇ0−1(x0−xˇ0),k=012(xk−Ak−1xk−1−vk)T×Qk−1(xk−Ak−1xk−1−vk),k=1…KJy,k(x)=12(yk−Ckxk)TRk−1(yk−Ckxk),k=0…K\begin{aligned} & J(\mathbf{x})=\sum_{k=0}^K\left(J_{v, k}(\mathbf{x})+J_{y, k}(\mathbf{x})\right) \\ & J_{v, k}(\mathbf{x})=\left\{\begin{array}{c} \frac{1}{2}\left(\mathbf{x}_0-\check{\mathbf{x}}_0\right)^T \check{\mathbf{P}}_0^{-1}\left(\mathbf{x}_0-\check{\mathbf{x}}_0\right), k=0 \\ \frac{1}{2}\left(\mathbf{x}_k-\mathbf{A}_{k-1} \mathbf{x}_{k-1}-\mathbf{v}_k\right)^T \\ \times \mathbf{Q}_k^{-1}\left(\mathbf{x}_k-\mathbf{A}_{k-1} \mathbf{x}_{k-1}-\mathbf{v}_k\right), k=1 \ldots K \end{array}\right. \\ & J_{y, k}(\mathbf{x})=\frac{1}{2}\left(\mathbf{y}_k-\mathbf{C}_k \mathbf{x}_k\right)^T \mathbf{R}_k^{-1}\left(\mathbf{y}_k-\mathbf{C}_k \mathbf{x}_k\right), \quad k=0 \ldots K \end{aligned} J(x)=k=0∑K(Jv,k(x)+Jy,k(x))Jv,k(x)=⎩⎨⎧21(x0−xˇ0)TPˇ0−1(x0−xˇ0),k=021(xk−Ak−1xk−1−vk)T×Qk−1(xk−Ak−1xk−1−vk),k=1…KJy,k(x)=21(yk−Ckxk)TRk−1(yk−Ckxk),k=0…K将上述模型整理为更简洁的形式,令
z=[xˇ0v1⋮vKy0y1⋮yK],x=[x0⋮xK]\mathbf{z}=\left[\begin{array}{c} \check{\mathbf{x}}_0 \\ \mathbf{v}_1 \\ \vdots \\ \mathbf{v}_K \\ \hline \mathbf{y}_0 \\ \mathbf{y}_1 \\ \vdots \\ \mathbf{y}_K \end{array}\right], \quad \mathbf{x}=\left[\begin{array}{c} \mathbf{x}_0 \\ \vdots \\ \mathbf{x}_K \end{array}\right] z=xˇ0v1⋮vKy0y1⋮yK,x=x0⋮xKH=[1−A01⋱⋱−AK−11C0C1⋱CK]W=[Pˇ0Q1⋱QKR0R1RK]\begin{aligned} & \mathbf{H}=\left[\begin{array}{cccc} \mathbf{1} & & & \\ -\mathbf{A}_0 & \mathbf{1} & & \\ & \ddots & \ddots & \\ & & -\mathbf{A}_{K-1} & \mathbf{1} \\ \hline \mathbf{C}_0 & \mathbf{C}_1 & & \\ & & \ddots & \\ & & & \mathbf{C}_K \end{array}\right] \\ & \mathbf{W}=\left[\begin{array}{llll|lll} \check{\mathbf{P}}_0 & & & & & & \\ & \mathbf{Q}_1 & & & & & \\ & & \ddots & & & \\ & & & \mathbf{Q}_K & & & \\ \hline & & & & \mathbf{R}_0 & & \\ & & & & & \mathbf{R}_1 & \\ & & & & & \mathbf{R}_K \end{array}\right] \\ & \end{aligned} H=1−A0C01⋱C1⋱−AK−1⋱1CKW=Pˇ0Q1⋱QKR0R1RK此时,目标函数可以重新表示为
J(x)=12(z−Hx)TW−1(z−Hx)J(\mathbf{x})=\frac{1}{2}(\mathbf{z}-\mathbf{H x})^T \mathbf{W}^{-1}(\mathbf{z}-\mathbf{H x}) J(x)=21(z−Hx)TW−1(z−Hx)求解其最小值,即令其一阶导为零
∂J(x)∂xT∣x^=−HTW−1(z−Hx^)=0\left.\frac{\partial J(\mathbf{x})}{\partial \mathbf{x}^T}\right|_{\hat{\mathbf{x}}}=-\mathbf{H}^T \mathbf{W}^{-1}(\mathbf{z}-\mathbf{H} \hat{\mathbf{x}})=\mathbf{0} ∂xT∂J(x)x^=−HTW−1(z−Hx^)=0即
(HTW−1H)x^=HTW−1z\left(\mathbf{H}^T \mathbf{W}^{-1} \mathbf{H}\right) \hat{\mathbf{x}}=\mathbf{H}^T \mathbf{W}^{-1} \mathbf{z} (HTW−1H)x^=HTW−1z然而,这是批量求解模型,当只关心当前时 刻(k时刻)状态时,应改为滤波模型。
假设上一时刻后验为
{x^k−1,P^k−1}\left\{\hat{\mathbf{x}}_{k-1}, \hat{\mathbf{P}}_{k-1}\right\} {x^k−1,P^k−1}
目标是得到当前时刻后验
{x^k−1,P^k−1,vk,yk}↦{x^k,P^k}\left\{\hat{\mathbf{x}}_{k-1}, \hat{\mathbf{P}}_{k-1}, \mathbf{v}_k, \mathbf{y}_k\right\} \mapsto\left\{\hat{\mathbf{x}}_k, \hat{\mathbf{P}}_k\right\} {x^k−1,P^k−1,vk,yk}↦{x^k,P^k}由于马尔可夫性,仅与前一时刻有关,因此令
zk=[x^k−1vkyk]Hk=[1−Ak−11Ck]Wk=[P^k−1QkRk]\begin{aligned} \mathbf{z}_k & =\left[\begin{array}{c} \hat{\mathbf{x}}_{k-1} \\ \mathbf{v}_k \\ \mathbf{y}_k \end{array}\right] \\ \mathbf{H}_k & =\left[\begin{array}{ccc} \mathbf{1} & \\ -\mathbf{A}_{k-1} & 1 \\ & \mathbf{C}_k \end{array}\right] \\ \mathbf{W}_k & =\left[\begin{array}{ccc} \hat{\mathbf{P}}_{k-1} & \\ & \mathbf{Q}_k & \\ & & \mathbf{R}_k \end{array}\right] \end{aligned} zkHkWk=x^k−1vkyk=1−Ak−11Ck=P^k−1QkRk则模型的解为
(HkTWk−1Hk)x^=HkTWk−1zk\left(\mathbf{H}_k^T \mathbf{W}_k^{-1} \mathbf{H}_k\right) \hat{\mathbf{x}}=\mathbf{H}_k^T \mathbf{W}_k^{-1} \mathbf{z}_k (HkTWk−1Hk)x^=HkTWk−1zk
其中
x^=[x^k−1′x^k]\hat{\mathbf{x}}=\left[\begin{array}{c} \hat{\mathbf{x}}_{k-1}^{\prime} \\ \hat{\mathbf{x}}_k \end{array}\right] x^=[x^k−1′x^k]x^k−1\hat{\mathbf{x}}_{k-1}x^k−1 和 x^k−1′\hat{\mathbf{x}}_{k-1}^{\prime}x^k−1′ 有本质区别,下图可以明确展示
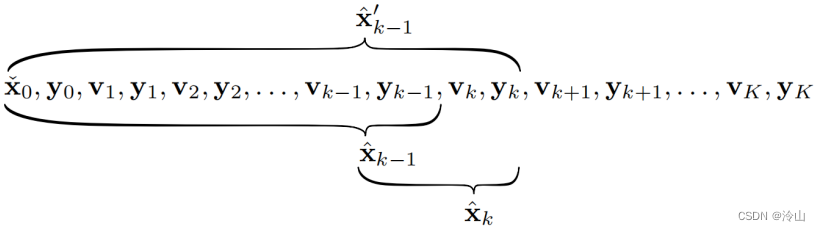
在此基础上,求解模型可以展开为
[P^k−1−1+Ak−1TQk−1Ak−1−Ak−1TQk−1−Qk−1Ak−1Qk−1+CkTRk−1Ck][x^k−1′x^k]=[P^k−1−1x^k−1−Ak−1TQk−1vkQk−1vk+CkTRk−1yk]\left[\begin{array}{cc} \hat{\mathbf{P}}_{k-1}^{-1}+\mathbf{A}_{k-1}^T \mathbf{Q}_k^{-1} \mathbf{A}_{k-1} & -\mathbf{A}_{k-1}^T \mathbf{Q}_k^{-1} \\ -\mathbf{Q}_k^{-1} \mathbf{A}_{k-1} & \mathbf{Q}_k^{-1}+\mathbf{C}_k^T \mathbf{R}_k^{-1} \mathbf{C}_k \end{array}\right]\left[\begin{array}{c} \hat{\mathbf{x}}_{k-1}^{\prime} \\ \hat{\mathbf{x}}_k \end{array}\right]=\left[\begin{array}{c} \hat{\mathbf{P}}_{k-1}^{-1} \hat{\mathbf{x}}_{k-1}-\mathbf{A}_{k-1}^T \mathbf{Q}_k^{-1} \mathbf{v}_k \\ \mathbf{Q}_k^{-1} \mathbf{v}_k+\mathbf{C}_k^T \mathbf{R}_k^{-1} \mathbf{y}_k \end{array}\right] [P^k−1−1+Ak−1TQk−1Ak−1−Qk−1Ak−1−Ak−1TQk−1Qk−1+CkTRk−1Ck][x^k−1′x^k]=[P^k−1−1x^k−1−Ak−1TQk−1vkQk−1vk+CkTRk−1yk]利用舒尔补,等式两边左乘如下矩阵,便可以直接求解出 x^k\hat{\mathbf{x}}_kx^k ,且不需求解 x^k−1′\hat{\mathbf{x}}_{k-1}^{\prime}x^k−1′
[10Qk−1Ak−1(P^k−1−1+Ak−1TQk−1Ak−1)−11]\left[\begin{array}{cc} \mathbf{1} & \mathbf{0} \\ \mathbf{Q}_k^{-1} \mathbf{A}_{k-1}\left(\hat{\mathbf{P}}_{k-1}^{-1}+\mathbf{A}_{k-1}^T \mathbf{Q}_k^{-1} \mathbf{A}_{k-1}\right)^{-1} & \mathbf{1} \end{array}\right] [1Qk−1Ak−1(P^k−1−1+Ak−1TQk−1Ak−1)−101]可得:
P^k−1x^k=Pˇk−1(Ak−1x^k−1+vk)+CkTRk−1yk\hat{\mathbf{P}}_k^{-1} \hat{\mathbf{x}}_k=\check{\mathbf{P}}_k^{-1}\left(\mathbf{A}_{k-1} \hat{\mathbf{x}}_{k-1}+\mathbf{v}_k\right)+\mathbf{C}_k^T \mathbf{R}_k^{-1} \mathbf{y}_k P^k−1x^k=Pˇk−1(Ak−1x^k−1+vk)+CkTRk−1yk其中
Pˇk=Qk+Ak−1P^k−1Ak−1TP^k=(Pˇk−1+CkTRk−1Ck)−1\begin{aligned} & \check{\mathbf{P}}_k=\mathbf{Q}_k+\mathbf{A}_{k-1} \hat{\mathbf{P}}_{k-1} \mathbf{A}_{k-1}^T \\ & \hat{\mathbf{P}}_k=\left(\check{\mathbf{P}}_k^{-1}+\mathbf{C}_k^T \mathbf{R}_k^{-1} \mathbf{C}_k\right)^{-1} \end{aligned} Pˇk=Qk+Ak−1P^k−1Ak−1TP^k=(Pˇk−1+CkTRk−1Ck)−1以上过程,核心即为边缘化,因此滤波(IEKF)可以看做长度为1的滑动窗口。
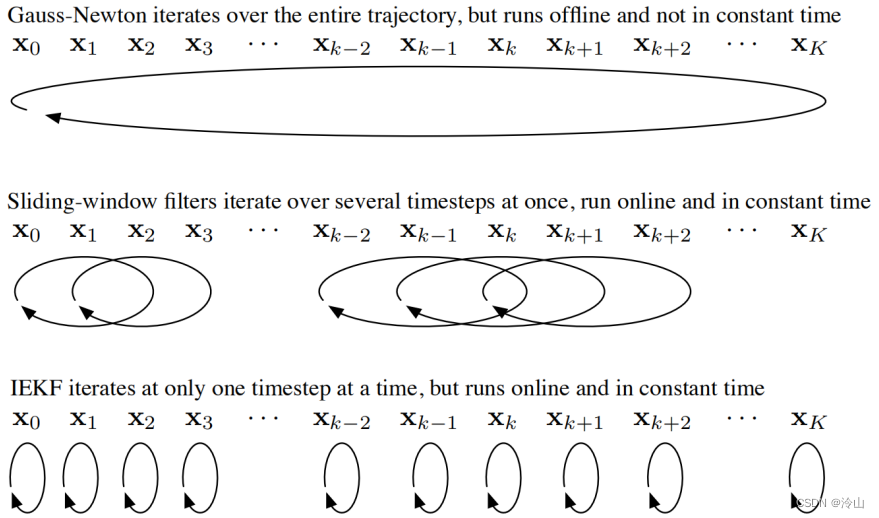
3. 基于kitti的实现原理
3.1 基于地图定位的滑动窗口模型
-
窗口优化模型构成
在图优化模型中,优化模型也可写成如下形式:
J⊤ΣJδx=−J⊤Σr\mathbf{J}^{\top} \boldsymbol{\Sigma} \mathbf{J} \delta \boldsymbol{x}=-\mathbf{J}^{\top} \boldsymbol{\Sigma} \mathbf{r} J⊤ΣJδx=−J⊤Σr其中
rrr 是残差;
JJJ 是残差关于状态量的雅可比;
∑\sum∑ 是信息矩阵。
在kitti工程中,基于地图定位的滑动窗口,其残差包括:- 地图匹配位姿和优化变量的残差
- 激光里程计相对位姿和优化变量的残差
- IMU预积分和优化变量的残差
- 边缘化形成的先验因子对应的残差
此处先介绍前3项,第4项待边缘化后介绍。
-
地图匹配位姿和优化变量的残差
该残差对应的因子为地图先验因子。
一个因子仅约束一个位姿,其模型如下:

残差关于优化变量的雅可比,可视化如下:

因此,对应的Hessian矩阵的可视化为:

-
激光里程计相对位姿和优化变量的残差
该残差对应的因子为激光里程计因子。
一个因子约束两个位姿,其模型如下:

残差关于优化变量的雅可比,可视化如下:

因此,对应的Hessian矩阵可视化为:

-
IMU预积分和优化变量的残差
该残差对应的因子为IMU因子。
一个因子约束两个位姿,并约束两个时刻 IMU
的速度与 bias。

残差关于优化变量的雅可比,可视化如下:

因此,对应的Hessian矩阵可视化为:

-
完整模型
完整Hessian矩阵,即为以上各因子对应矩阵的累加。

上述过程用公式可表示为:
J⊤ΣJ⏟Hδx=−J⊤Σr⏟b \underbrace{\mathbf{J}^{\top} \boldsymbol{\Sigma} \mathbf{J}}_{\mathbf{H}} \delta \boldsymbol{x}=\underbrace{-\mathbf{J}^{\top} \boldsymbol{\Sigma} \boldsymbol{r}}_{\text {b }} HJ⊤ΣJδx=b −J⊤Σr其中
r=[rY0rY1rY2rL0rL1rM0rM1]\boldsymbol{r}=\left[\begin{array}{l} \boldsymbol{r}_{Y 0} \\ \boldsymbol{r}_{Y 1} \\ \boldsymbol{r}_{Y 2} \\ \boldsymbol{r}_{L 0} \\ \boldsymbol{r}_{L 1} \\ \boldsymbol{r}_{M 0} \\ \boldsymbol{r}_{M 1} \end{array}\right] r=rY0rY1rY2rL0rL1rM0rM1
J=∂r∂δx=[∂r0∂δ0∂r1∂δx∂r2∂δx∂rL0∂δx∂rL1∂δx∂rM0∂δx∂rM1∂δx]=[J1J2J3J4J5J6J7]J⊤=[J1⊤J2⊤J3⊤J4⊤J5⊤J6⊤J7⊤]\begin{aligned} & \mathbf{J}=\frac{\partial \mathbf{r}}{\partial \delta x}=\left[\begin{array}{c} \frac{\partial \mathbf{r}_0}{\partial \delta_0} \\ \frac{\partial \mathbf{r}_1}{\partial \delta x} \\ \frac{\partial \mathbf{r}_2}{\partial \delta x} \\ \frac{\partial \mathbf{r}_{L 0}}{\partial \delta x} \\ \frac{\partial \mathbf{r}_{L 1}}{\partial \delta x} \\ \frac{\partial \mathbf{r}_{M 0}}{\partial \delta x} \\ \frac{\partial \mathbf{r}_{M 1}}{\partial \delta x} \end{array}\right]=\left[\begin{array}{l} \mathbf{J}_1 \\ \mathbf{J}_2 \\ \mathbf{J}_3 \\ \mathbf{J}_4 \\ \mathbf{J}_5 \\ \mathbf{J}_6 \\ \mathbf{J}_7 \end{array}\right] \\ & \mathbf{J}^{\top}=\left[\begin{array}{lllllll} \mathbf{J}_1^{\top} & \mathbf{J}_2^{\top} & \mathbf{J}_3^{\top} & \mathbf{J}_4^{\top} & \mathbf{J}_5^{\top} & \mathbf{J}_6^{\top} & \mathbf{J}_7^{\top} \end{array}\right] \\ & \end{aligned} J=∂δx∂r=∂δ0∂r0∂δx∂r1∂δx∂r2∂δx∂rL0∂δx∂rL1∂δx∂rM0∂δx∂rM1=J1J2J3J4J5J6J7J⊤=[J1⊤J2⊤J3⊤J4⊤J5⊤J6⊤J7⊤]矩阵乘法写成累加形式为:
∑i=17Ji⊤ΣiJiδx=−∑i=17Ji⊤Σiri\sum_{i=1}^7 \mathbf{J}_i^{\top} \boldsymbol{\Sigma}_i \mathbf{J}_i \delta \boldsymbol{x}=-\sum_{i=1}^7 \mathbf{J}_i^{\top} \boldsymbol{\Sigma}_i \mathbf{r}_i i=1∑7Ji⊤ΣiJiδx=−i=1∑7Ji⊤Σiri此累加过程,即对应前面可视化时各矩阵叠加。
3.2 边缘化过程
-
移除老的帧
假设窗口长度为3,在加入新的帧之前,需要先边缘化掉老的帧,即下图方框中的变量。
 用前述公式,可以表示为
用前述公式,可以表示为
(Hrr−HrmHmm−1Hmr)δxr=br−HrmHmm−1bm\left(H_{r r}-H_{r m} H_{m m}^{-1} H_{m r}\right) \delta x_r=b_r-H_{r m} H_{m m}^{-1} b_m (Hrr−HrmHmm−1Hmr)δxr=br−HrmHmm−1bm但是在实际代码中,会把它拆成两步实现。第一步:使用和要边缘化掉的量无关的因子,构建剩余变量对应的Hessian矩阵。

上标 aaa 代表是第一步中的变量,包含Hessian矩阵的完整表达式为
Hrraδxr=braH_{r r}^a \delta x_r=b_r^a Hrraδxr=bra第二步:挑出和要边缘化掉的量相关的因子,构建待边缘化的Hessian矩阵,并使用舒尔补做边缘化。

上标 bbb 代表是第二步中的变量,包含Hessian矩阵的完整表达式为
[Hrrb−Hrmb(Hmmb)−1Hmrb]δxr=brb−Hrmb(Hmmb)−1bmb\left[H_{r r}^b-H_{r m}^b\left(H_{m m}^b\right)^{-1} H_{m r}^b\right] \delta x_r=b_r^b-H_{r m}^b\left(H_{m m}^b\right)^{-1} b_m^b [Hrrb−Hrmb(Hmmb)−1Hmrb]δxr=brb−Hrmb(Hmmb)−1bmb这一步形成的约束(上式)就叫先验因子,它包含了边缘化掉的量对剩余变量的约束关系。
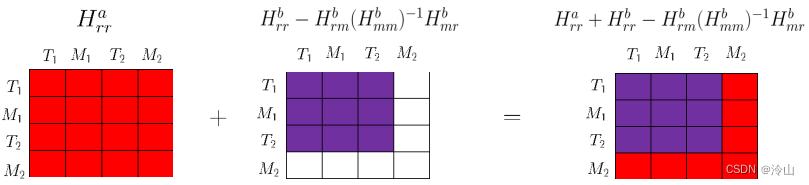
最终使用的是两步的叠加,Hessian矩阵叠加的可视化如下:
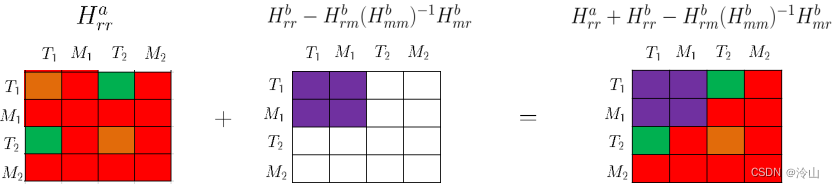
对应的完整公式为
Hrrδxr=brH_{r r} \delta x_r=b_r Hrrδxr=br其中
Hrr=Hrra+Hrrb−Hrmb(Hmmb)−1Hmrbbr=bra+brb−Hrmb(Hmmb)−1bmb\begin{gathered} H_{r r}=H_{r r}^a+H_{r r}^b-H_{r m}^b\left(H_{m m}^b\right)^{-1} H_{m r}^b \\ b_r=b_r^a+b_r^b-H_{r m}^b\left(H_{m m}^b\right)^{-1} b_m^b \end{gathered} Hrr=Hrra+Hrrb−Hrmb(Hmmb)−1Hmrbbr=bra+brb−Hrmb(Hmmb)−1bmb边缘化之后,模型如下:

注意:边缘化先验因子只有在第一次边缘化之前是不存在的,完成第一次边缘化之后就一直存在,并且随着后续新的边缘化进行,其内容不断更新。 -
添加新的帧
添加新的帧之后,模型如下:

此处直接给出新的Hessian矩阵可视化结果:

此后,随着定位过程的进行,便不断循环“边缘化老帧->添加新帧”的过程,从而维持窗口长度不变。
该过程的代码实现可参考后面lio-mapping的实现,理解后者便很容易实现前者。
4. lio-mapping 介绍
4.1 核心思想

基于滑动窗口方法,把雷达线/面特征、IMU预积分等的约束放在一起进行优化。
- 𝑜𝑜o 到 𝑖𝑖i 是滑窗;
- 只有 𝑝𝑝p 到 𝑖𝑖i 的位姿在滑窗中优化;
- 𝑜𝑜o 到 𝑝𝑝p 是为了构建局部地图,防止地图过于稀疏;
- 局部地图都投影到 𝑝𝑝p 的位姿处;
- 滑窗中点云约束是当前优化帧和局部地图特征匹配,因此特征对应的因子约束的是 𝑝𝑝p 帧和 𝑘𝑘k 帧(𝑝𝑝p<𝑘𝑘k<=𝑗𝑗j)。
其优化模型为
minX12{∥rP(X)∥2+∑m∈mLαα∈{p+1,⋯,j}∥rL(m,X)∥CLαm2+∑β∈{p,⋯,j−1}∥rB(zβ+1β,X)∥CBβ+1Bβ2}\begin{aligned} & \min _{\mathbf{X}} \frac{1}{2}\left\{\left\|\mathbf{r}_{\mathcal{P}}(\mathbf{X})\right\|^2+\sum_{\substack{m \in \mathbf{m}_{L_\alpha} \\ \alpha \in\{p+1, \cdots, j\}}}\left\|\mathbf{r}_{\mathcal{L}}(m, \mathbf{X})\right\|_{\mathbf{C}_{L_\alpha}^m}^2\right. \\ & \left.+\sum_{\beta \in\{p, \cdots, j-1\}}\left\|\mathbf{r}_{\mathcal{B}}\left(z_{\beta+1}^\beta, \mathbf{X}\right)\right\|_{\mathbf{C}_{B_{\beta+1}}^{B_\beta}}^2\right\} \end{aligned} Xmin21⎩⎨⎧∥rP(X)∥2+m∈mLαα∈{p+1,⋯,j}∑∥rL(m,X)∥CLαm2+β∈{p,⋯,j−1}∑rB(zβ+1β,X)CBβ+1Bβ2⎭⎬⎫其中
rP(X)\mathbf{r}_{\mathcal{P}}(\mathbf{X})rP(X) 是边缘化产生的先验因子对应的残差;
rL(m,X)\mathbf{r}_{\mathcal{L}}(m, \mathbf{X})rL(m,X) 是点云特征匹配对应的残差;
rB(zβ+1β,X)\mathbf{r}_{\mathcal{B}}\left(z_{\beta+1}^\beta, \mathbf{X}\right)rB(zβ+1β,X) 是IMU约束对应的残差。
4.2 具体流程
流程讲解思路:
• 以前述kitti中实现原理为基础,此处只是多了点云特征的约束;
• 只介绍可借鉴的内容,因此不介绍bias、外参初始化和外参优化等内容。
4.2.1 各类因子
-
定义IMU 因子
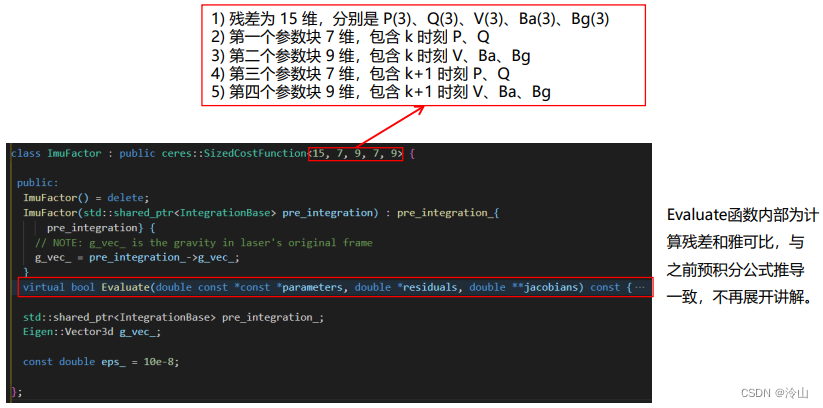
-
添加imu因子
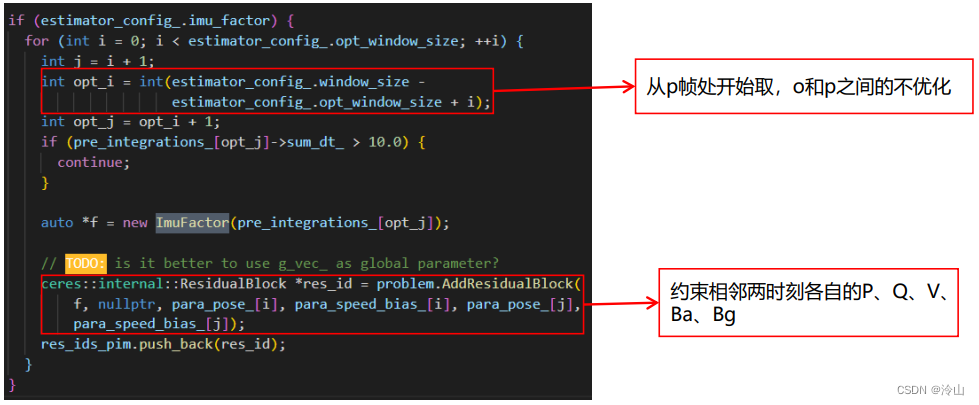
-
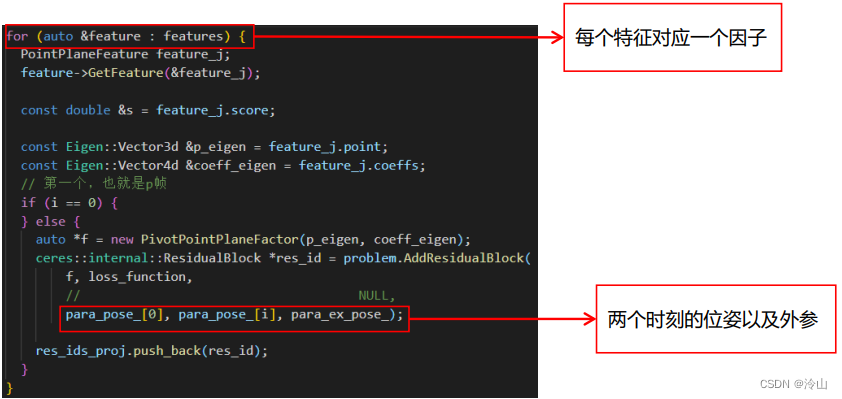
定义点云面特征因子
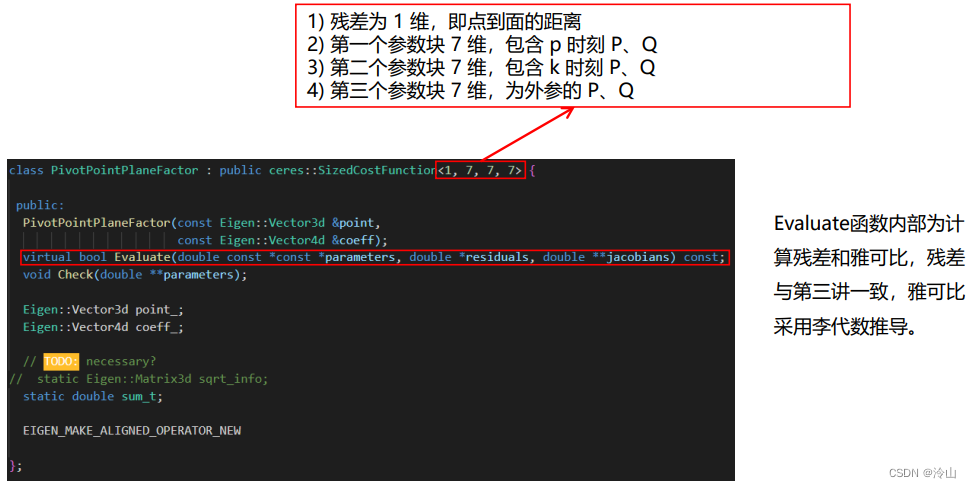
-
添加点云面特征
-
定义边缘化先验因子

由于不确定边缘化后会和哪些量产生关联,因此没有固定size。
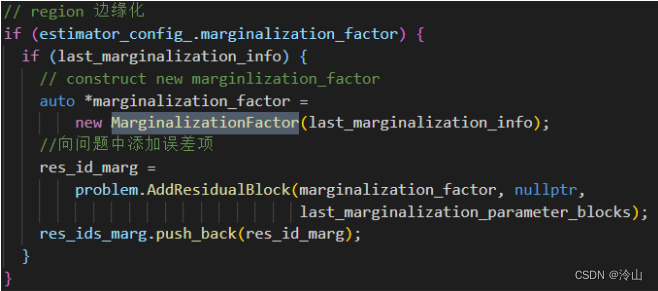
其详细内容待讲解边缘化实现时再展开。 -
添加边缘化先验因子
4.2.2 滑窗模型
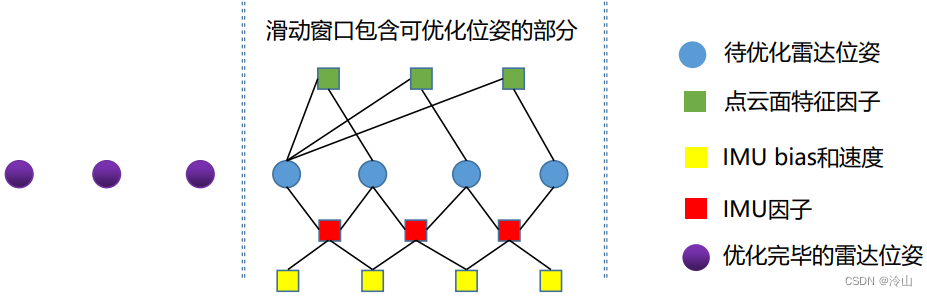
• 帧与帧之间通过特征约束,因此没有了激光里程计因子。
• 当前模型中没有使用点云的线特征。
-
IMU预积分和优化变量的残差
一个因子约束两个位姿,并约束两个时刻 IMU 的速度与 bias

残差关于优化变量的雅可比可视化如下:

因此对应的Hessian矩阵的可视化为:

-
点云面特征对应的残差
一个因子约束两个位姿

残差关于优化变量的雅可比可视化如下:

因此对应的Hessian矩阵的可视化为

-
完整模型
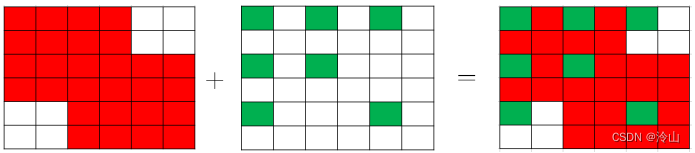 以上工程,就是前述代码中添加各类因子到模型的过程。
以上工程,就是前述代码中添加各类因子到模型的过程。
4.2.3 边缘化
-
边缘化模型

需要边缘化掉的为方框中的变量 -
边缘化可视化
第一步:使用和要边缘化掉的量无关的因子,构建剩余变量对应的Hessian矩阵。

第二步:挑出和要边缘化掉的量相关的因子,构建待边缘化的Hessian矩阵,并使用舒尔补做边缘化。

对应的完整Hessian矩阵就是他们合在一起的结果。
-
边缘化实现
核心思路是把要边缘化掉的变量,以及跟这些变量被同一个因子约束的变量,汇总在一起。
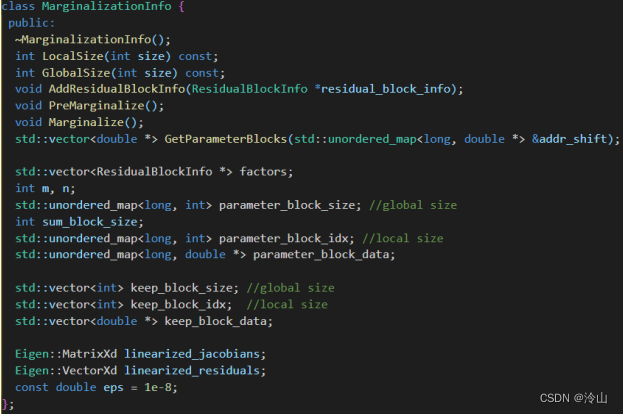
在该例中,把和模型无关的量去除,剩余部分如下(设每帧有20个面特征)
因此,放入MarginalizationInfo中的信息包括:
5个变量: T0M0T1M1T2T_0 \quad M_0 \quad T_1 \quad M_1 T_2T0M0T1M1T2
41个因子: 40 个面特征因子、1个IMU因子
(此处假设的是第一次进行边缘化,若不是第 一次,因子中还应该有边缘化先验因子)
找出所有变量后,需要知道哪些是应该边缘化的,哪些是应该保留的。
右图代码中,形参里_parameter_blocks包含所有相关参数,而_drop_set即为这些参数中要边缘化掉的参数的id。
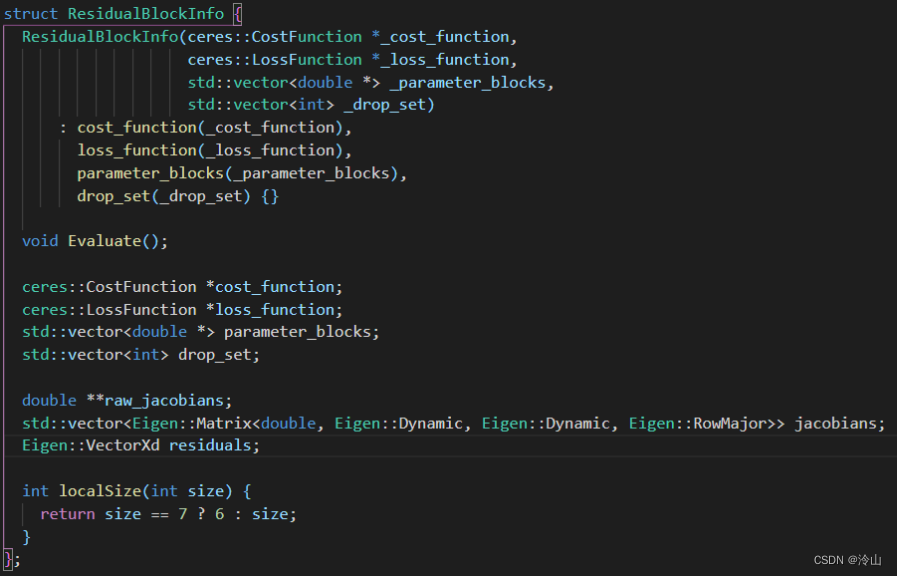
添加和IMU因子相关的ResidualBlockInfo
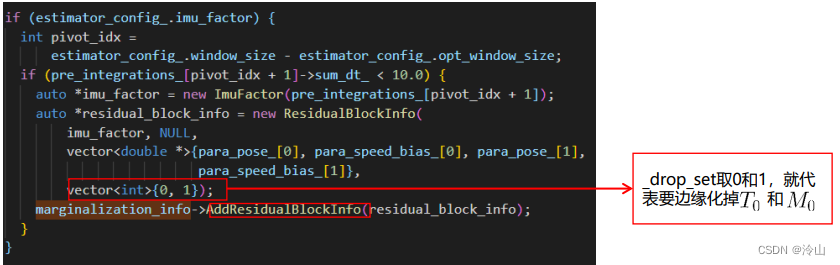
添加和面特征因子相关的ResidualBlockInfo
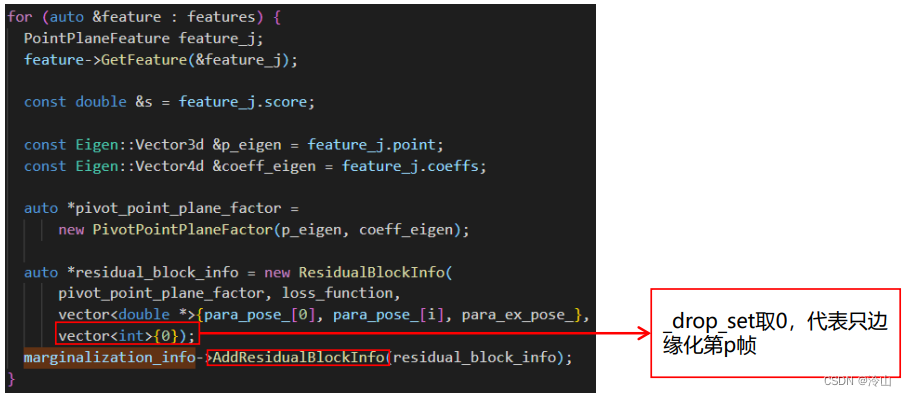
在添加以上ResidualBlockInfo的同时,核心变量parameter_block_size 就被赋值。
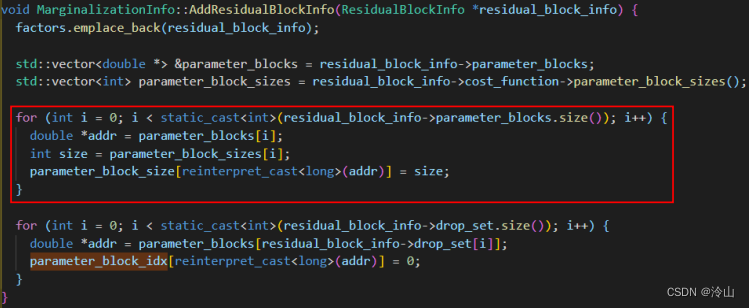
第二个核心函数的作用是计算每个因子对应的变量(parameter_blocks)、误差项(residuals)、雅可比矩阵(jacobians),并把变量数值放到parameter_block_data中。
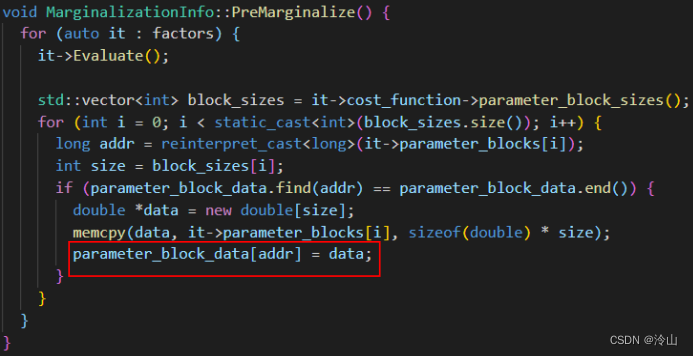
第三个核心函数的作用构建Hessian矩阵,Schur掉需要marg的变量,得到对剩余变量的约束,即为边缘化约束(先验约束)。
函数的前半部分,对m、n和parameter_block_idx 这三个核心变量进行了赋值。
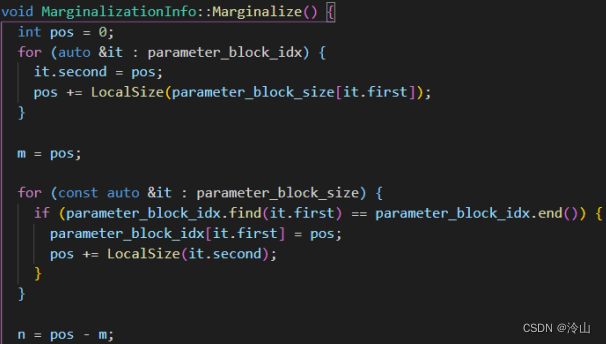
函数的中间部分开始构建Hessian 矩阵,由于使用多线程,因此要给不同的线程平均分配因子。
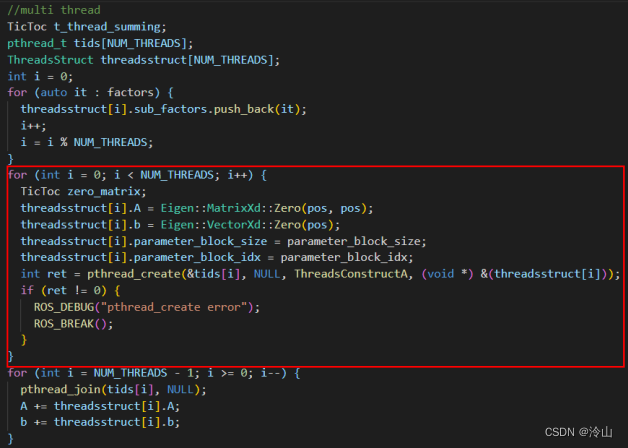
函数的最后便是执行边缘化,得到边缘化先验因子。
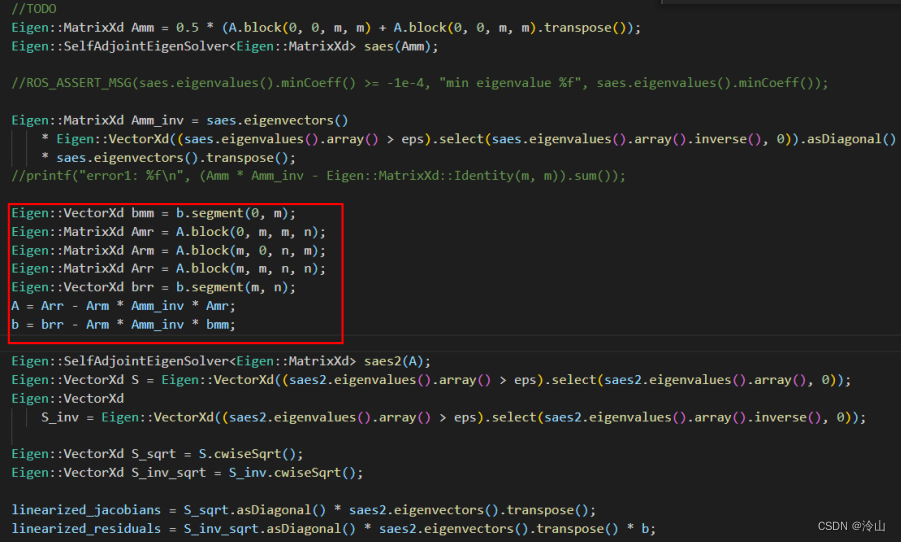
上述过程是假设第一次执行边缘化,当不是第一次时,步骤上只是多了在AddResidualBlockInfo时把边缘化先验因子也加入进来,剩余过程不变。
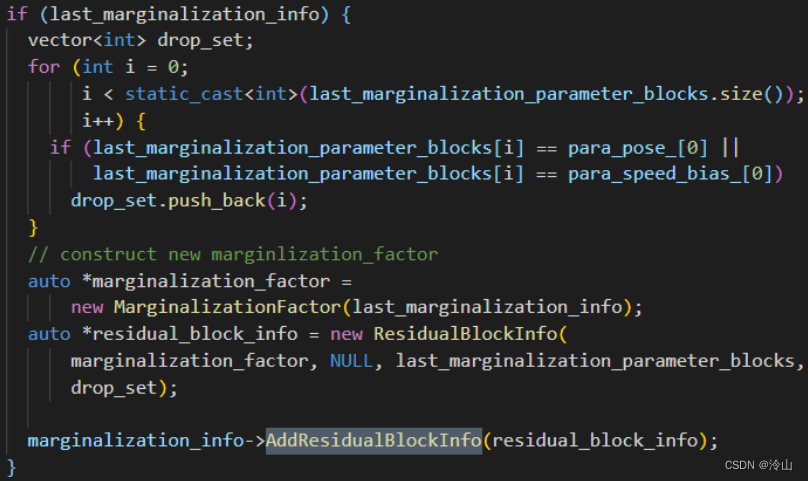
4.2.4 添加新帧
边缘化之后,模型如下:

注意:由于面特征因子都是和第一帧(T0T_0T0)关联,当它边缘化掉之后,该因子便不存在,因此在加入新的帧的同时,还需要构建所有帧和当前第一帧(T1T_1T1)的面特征关联。
添加新的帧以后,模型如下:

Hessian矩阵可视化如下:

此后不断循环该过程,便可以实现lio功能。
相关文章:

多传感器融合定位十四-基于图优化的定位方法
多传感器融合定位十四-基于图优化的定位方法1. 基于图优化的定位简介1.1 核心思路1.2 定位流程2. 边缘化原理及应用2.1 边缘化原理2.2 从滤波角度理解边缘化3. 基于kitti的实现原理3.1 基于地图定位的滑动窗口模型3.2 边缘化过程4. lio-mapping 介绍4.1 核心思想4.2 具体流程4.…...

PHP基于TCPDF第三方类生成PDF文件
最近在研发招聘的系统 遇到了这个问题 转换pdf 折腾了很久 分享一下PHP基于TCPDF第三方类生成PDF文件最近遇到一个需求,需要根据数据库的字段生成表格式的PDF文件并发送邮箱第一步、我们先去官网上面去下载tcpdf的类:http://www.tcpdf.org/或者是从githu…...
:Sentinel定义资源的方式)
SpringCloud(19):Sentinel定义资源的方式
Sentinel除了基本的定义资源的方式之外,还有其他的定义资源的方式,具体如下: 抛出异常的方式定义资源返回布尔值方式定义资源异步调用支持注解方式定义资源主流框架的默认适配1 抛出异常的方式定义资源 Sentinel中的SphU包含了try-catch风格的API。用这种方式,当资源发生了…...

前端 ES6 之 Promise 实践应用与控制反转
Promise 主要是为解决程序异步处理而生的,在现在的前端应用中无处不在,已然成为前端开发中最重要的技能点之一。它不仅解决了以前回调函数地狱嵌套的痛点,更重要的是它提供了更完整、更强大的异步解决方案。 同时 Promise 也是前端面试中必不…...

LightGBM
目录 1.LightGBM的直方图算法(Histogram) 直方图做差加速 2.LightGBM得两大先进技术(GOSS&EFB) 2.1 单边梯度抽样算法(GOSS) 2.2 互斥特征捆绑算法(EFB) 3.LightGBM得生长策略(leaf-wise) 通过与xgboost对比,在这里列出lgb新提出的几个方面的技术 1.Ligh…...
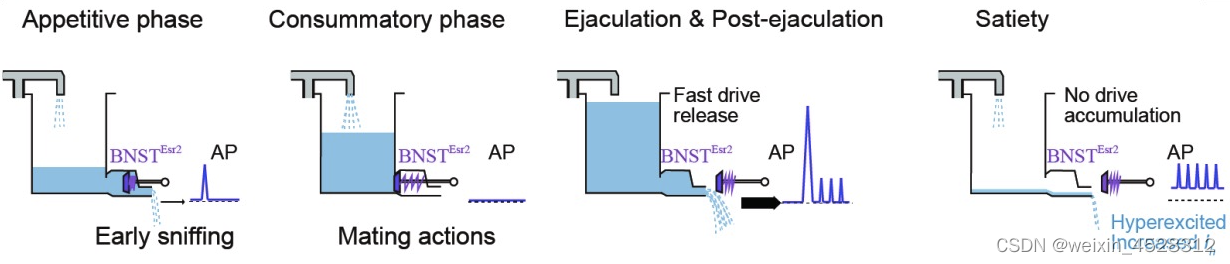
Science:北京脑研究中心李莹实验室揭示性满足感的分子机制
短暂的社交经历(例如,性经历)可导致内部状态的长期变化并影响社会行为,如交配、攻击。例如,在成功交配射精后,许多物种迅速表现出对交配倾向的抑制有数小时、数天或更长时间,这种效应称为性满足…...

Element UI框架学习篇(三)
Element UI框架学习篇(三) 实现简单登录功能(不含记住密码) 1 准备工作 1.1 在zlz包下创建dto包,并创建userDTO类(传输对象) package com.zlz.dto;import lombok.Data;/* DTO 数据传输对象 用户表的传输对象 调用控制器传参使用 VO 控制器返回的视图对象 与页面对应 PO 数据…...
尚硅谷的尚融宝项目
先建立一个Maven springboot项目 进来先把src删掉,因为是一个父项目,我们删掉src之后,pom里配置的东西,也能给别的模块使用。 改一下springboot的版本号码 加入依赖和依赖管理: <properties><java.versi…...

12 Day:内存管理
前言:今天我们要完成我们操作系统的内存管理,以及一些数据结构和小组件的实现,在此之前大家需要了解我们前几天一些重要文件的内存地址存放在哪,以便我们更好的去编写内存管理模块 一,实现ASSERT断言 不知道大家有没有…...

linux基本功系列之lsof命令实战
文章目录前言一. lsof命令介绍二. 语法格式及常用选项三. 参考案例3.1 显示系统打开的文件3.2 查找某个文件相关的进程3.3 列出某个用户打开的文件信息3.4 列出某个程序进程所打开的文件信息3.5 查看某个进程号打开的文件3.6 列出所有的网络连接3.7 列出谁在使用某个端口3.8 恢…...
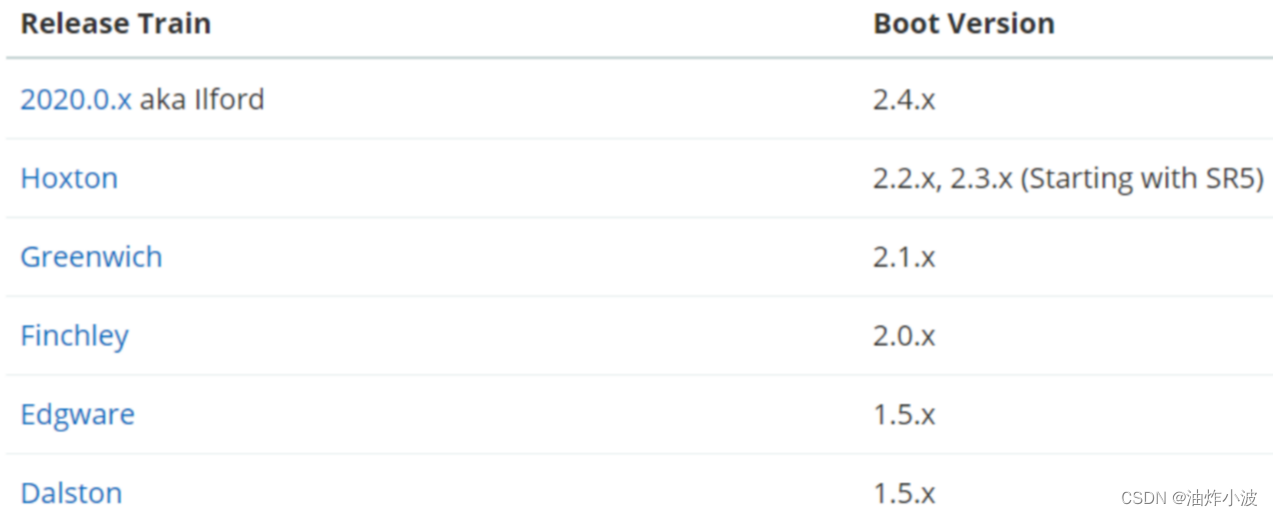
基础篇:02-SpringCloud概述
1.SpringCloud诞生 基于前面章节,我们深知微服务已成为当前开发的主流技术栈,但是如dubbo、zookeeper、nacos、rocketmq、rabbitmq、springboot、redis、es这般众多技术都只解决了一个或一类问题,微服务并没有一个统一的解决方案。开发人员或…...
【软件测试】软件测试工作上95%会遇到的问题,你遇到多少?
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 1、测试负责人要进行…...

4.5.4 LinkedList
文章目录1.特点2.常用方法3.练习:LinkedList测试1.特点 链表,两端效率高,底层就是链表实现的 List接口的实现类,底层的数据结构为链表,内存空间是不连续的 元素有下标,有序允许存放重复的元素在数据量较大的情况下,查询慢&am…...

Python之FileNotFoundError: [Errno 2] No such file or directory问题处理
错误信息:FileNotFoundError: [Errno 2] No such file or directory: ../AutoFrame/temp/report.xlsx相对于当前文件夹的路径,其实就是你写的py文件所在的文件夹路径!python在对文件的操作时,需要特别注意文件地址的书写。文件的路…...

C语言中耳熟能详的printf与scanf
没有什么比时间更有说服力了,因为时间无需通知我们就可以改变一切了。---余华《活着》大家好,今天给大家分享的是C语言中的scanf与printf函数,一提起这两个函数,大家可能觉得这不就是打印和输入嘛?有什么可以说的&…...
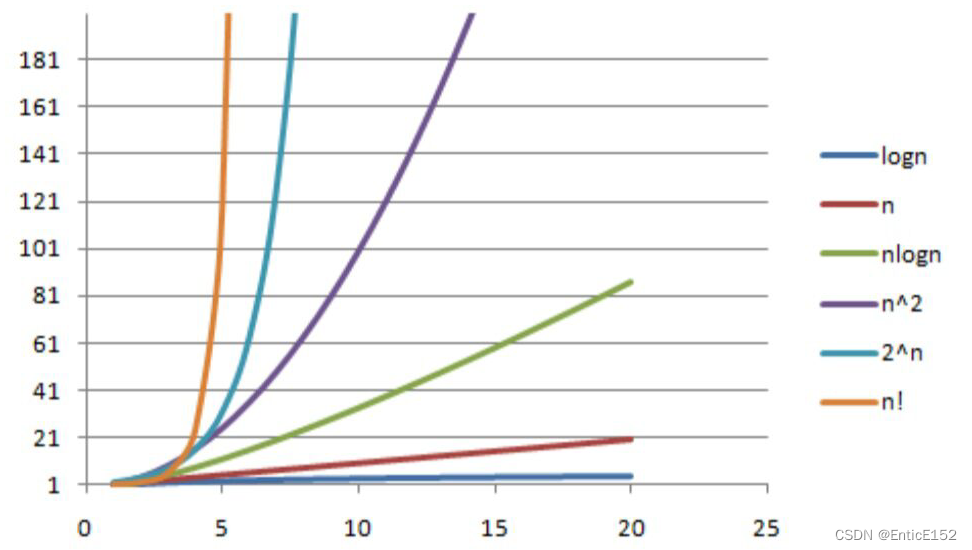
【数据结构】复杂度讲解
目录 时间复杂度与空间复杂度:: 1.算法效率 2.时间复杂度 3.空间复杂度 4.常见时间复杂度以及复杂度OJ练习 时间复杂度与空间复杂度:: 什么是数据结构? 数据结构中是计算机存储,组织数据的方式,指相互之间存在一种或多种特定关…...

JAVA-线程池技术
目录 概念 什么是线程? 什么是线程池? 线程池出现背景 线程池原理图 JAVA提供线程池 线程池参数 如果本篇博客对您有一定的帮助,大家记得留言点赞收藏哦。 概念 什么是线程? 是操作系统能够进行运算调度的最小单位。&am…...
)
【C++】从0到1入门C++编程学习笔记 - 提高编程篇:STL常用算法(算术生成算法)
文章目录一、accumulate二、fill学习目标: 掌握常用的算术生成算法 注意: 算术生成算法属于小型算法,使用时包含的头文件为 #include <numeric> 算法简介: accumulate // 计算容器元素累计总和 fill // 向容器中添加元…...

【C++】static成员
💙作者:阿润菜菜 📖专栏:C 目录 概念 特性 出个题 概念 声明为static的类成员称为类的静态成员,用static修饰的成员变量,称之为静态成员变量; 用static修饰的成员函数,称之为静态…...
Python Scrapy 爬虫简单教程
1. Scrapy install 准备知识 pip 包管理Python 安装XpathCssWindows安装 Scrapy $>- pip install scrapy Linux安装 Scrapy $>- apt-get install python-scrapy 2. Scrapy 项目创建 在开始爬取之前,必须创建一个新的Scrapy项目。进入自定义的项目目录中&am…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...
