机器学习:基于梯度下降算法的线性拟合实现和原理解析
机器学习:基于梯度下降算法的线性拟合实现和原理解析
- 线性拟合
- 梯度下降
- 算法步骤
- 算法实现
- 数据可视化(动态展示)
- 应用示例
当我们需要寻找数据中的趋势、模式或关系时,线性拟合和梯度下降是两个强大的工具。这两个概念在统计学、机器学习和数据科学领域都起着关键作用。本篇博客将介绍线性拟合和梯度下降的基本原理,以及它们在实际问题中的应用。
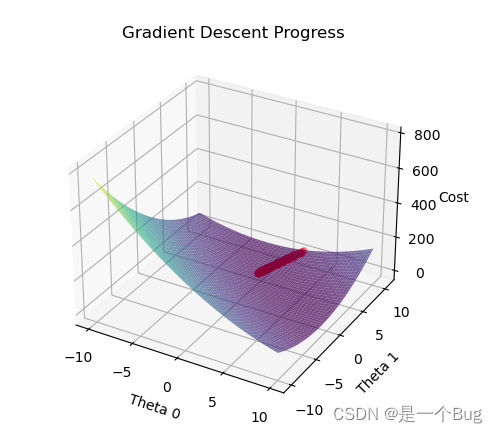
线性拟合
线性拟合是一种用于找到数据集中线性关系的方法。它的基本原理是,我们可以使用线性方程来描述两个或多个变量之间的关系。这个方程通常采用以下形式:
y = m x + b y=mx+b y=mx+b
在这个方程中, y y y 是因变量, x x x 是自变量, m m m 是斜率, b b b 是截距。线性拟合的目标是找到最佳的斜率和截距,以使线性方程最好地拟合数据。
为了找到最佳拟合线,我们通常使用最小二乘法。这意味着我们将所有数据点到拟合线的距离的平方相加,然后寻找最小化这个总和的斜率和截距。这可以用数学优化方法来实现,其中一个常用的方法就是梯度下降。
梯度下降
梯度下降是一种迭代优化算法,用于寻找函数的最小值。在线性拟合中,我们的目标是最小化误差函数,即数据点到拟合线的距离的平方和。这个误差函数通常表示为 J ( m , b ) J(m, b) J(m,b),其中 m m m 是斜率, b b b 是截距。我们的任务是找到 m m m 和 b b b 的值,使 J ( m , b ) J(m, b) J(m,b) 最小化。
梯度下降的基本思想是从一个随机初始点开始,然后根据误差函数的梯度方向逐步调整参数,直到找到局部最小值。梯度下降的迭代规则如下:
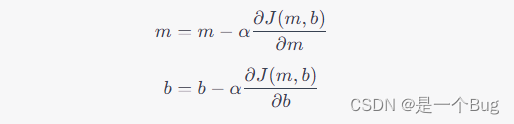
在这里, α \alpha α 是学习率,它决定了每次迭代中参数更新的步长。较大的学习率可能导致快速收敛,但可能会错过最小值,而较小的学习率可能需要更多的迭代。
算法步骤
线性回归中的梯度下降是一种优化算法,用于寻找最佳拟合线性模型的参数,以最小化预测值与实际观测值之间的均方误差(Mean Squared Error,MSE)。梯度下降的原理可以概括为以下几个步骤:
初始化参数: 首先,为线性回归模型的参数(权重和偏置项)选择初始值。通常,可以随机初始化这些参数。
计算损失函数: 使用当前的参数值,计算出模型的预测值,并计算预测值与实际观测值之间的差异,即损失函数。在线性回归中,常用的损失函数是均方误差(MSE),它表示为:
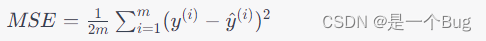
其中, m m m 是样本数量, y ( i ) y^{(i)} y(i) 是第 i i i 个观测值, y ^ ( i ) \hat{y}^{(i)} y^(i) 是模型的预测值。
计算梯度: 梯度是损失函数关于参数的偏导数,表示了损失函数在参数空间中的变化方向。梯度下降算法通过计算损失函数关于参数的梯度来确定参数更新的方向。对于线性回归模型,梯度可以表示为:
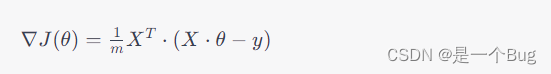
其中, J ( θ ) J(\theta) J(θ) 是损失函数, θ \theta θ 是参数向量, X X X 是特征矩阵, y y y 是目标向量。
参数更新: 使用梯度信息,按照下面的规则来更新参数:
θ = θ − α ∇ J ( θ ) θ=θ−α∇J(θ) θ=θ−α∇J(θ)
其中, α \alpha α 是学习率,它控制着每次参数更新的步长。学习率越小,参数更新越小,但收敛可能会更稳定。学习率越大,参数更新越快,但可能会导致不稳定的收敛或发散。
重复迭代: 重复执行步骤2至步骤4,直到满足停止条件,例如达到最大迭代次数或损失函数收敛到一个足够小的值。在每次迭代中,参数都会根据梯度信息进行更新,逐渐优化以减小损失函数。
梯度下降的目标是找到损失函数的最小值,这将使线性回归模型的预测值与实际观测值之间的误差最小化。通过不断调整参数,梯度下降可以使模型逐渐收敛到最佳参数值,从而得到最佳拟合线性模型。
算法实现
import numpy as np
import matplotlib.pyplot as plt
# 设置字体为支持汉字的字体(例如宋体)
plt.rcParams['font.sans-serif'] = ['SimSun']
# 创建示例数据
X = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 5, 4, 5])# 添加偏置项(截距项)到特征矩阵
# 添加了偏置项(截距项)到特征矩阵 X。这是通过在 X 前面添加一列全为1的列来实现的。这是线性回归模型中的常见步骤。
X_b = np.c_[np.ones((len(X), 1)), X.reshape(-1, 1)]# 使用正规方程计算最佳参数
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)# 使用梯度下降计算最佳参数
def gradient_descent(X_b, y, theta, learning_rate, num_epochs):m = len(y)losses = []for epoch in range(num_epochs):# 计算当前参数下的预测值。predictions = X_b.dot(theta)error = predictions - y# 计算均方误差(MSE)作为损失函数,衡量预测值和实际值之间的差异。loss = np.mean(error**2)# 计算损失函数的梯度,用于更新参数。# X_b.T 表示矩阵 X_b 的转置。在线性代数中,矩阵的转置是指将矩阵的行和列交换,即将矩阵的列向量变成行向量,反之亦然。gradient = 2 * X_b.T.dot(error) / mtheta -= learning_rate * gradientlosses.append(loss)return theta, lossestheta = np.random.randn(2)
learning_rate = 0.01
num_epochs = 1000
theta, losses = gradient_descent(X_b, y, theta, learning_rate, num_epochs)# 可视化数据和拟合结果
plt.scatter(X, y, label='数据点')
plt.plot(X, X_b.dot(theta_best), label='正规方程拟合', color='green')
plt.plot(X, X_b.dot(theta), label='梯度下降拟合', color='red')
plt.xlabel('特征值')
plt.ylabel('目标值')
plt.legend()
plt.show()数据可视化(动态展示)
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation# 创建一些示例数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.rand(100, 1)# 初始化线性模型参数
theta = np.random.randn(2, 1)def gradient_descent(X, y, theta, learning_rate, num_iterations):m = len(y)history = []for iteration in range(num_iterations):gradients = -2/m * X.T.dot(y - X.dot(theta))theta -= learning_rate * gradientshistory.append(theta.copy())return historylearning_rate = 0.1
num_iterations = 50# 添加偏置项
X_b = np.c_[np.ones((100, 1)), X]# 执行梯度下降算法并获取参数历史
parameter_history = gradient_descent(X_b, y, theta, learning_rate, num_iterations)# 创建动态可视化
fig, ax = plt.subplots()
line, = ax.plot([], [], lw=2)def animate(i):y_pred = X_b.dot(parameter_history[i])line.set_data(X, y_pred)return line,ani = FuncAnimation(fig, animate, frames=num_iterations, interval=200)
plt.scatter(X, y)
plt.xlabel('X')
plt.ylabel('y')
plt.title('Linear Regression with Gradient Descent')plt.show()
应用示例
线性拟合和梯度下降在各种领域都有广泛的应用。以下是一些示例:
股市预测:通过线性拟合历史股票价格数据,可以尝试预测未来股价的趋势。
房价预测:使用线性拟合来估算房屋价格与特征(如面积、位置等)之间的关系,帮助买家和卖家做出决策。
机器学习模型训练:梯度下降是训练线性回归、逻辑回归和神经网络等机器学习模型的关键步骤。
自然语言处理:在自然语言处理中,线性拟合可以用于情感分析和文本分类任务。
总之,线性拟合和梯度下降是数据科学和机器学习领域的基本工具,它们帮助我们理解数据中的关系,并训练模型以做出预测和决策。这两个概念的理解对于处理各种数据分析和机器学习问题都至关重要。希望本博客能够帮助你更好地理解它们的基本原理和应用。
相关文章:
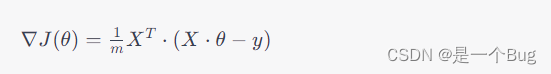
机器学习:基于梯度下降算法的线性拟合实现和原理解析
机器学习:基于梯度下降算法的线性拟合实现和原理解析 线性拟合梯度下降算法步骤算法实现数据可视化(动态展示)应用示例 当我们需要寻找数据中的趋势、模式或关系时,线性拟合和梯度下降是两个强大的工具。这两个概念在统计学、机器…...

关键点数据增强
1.关键点数据增强 # 关键点数据增强 from PIL import Image, ImageDraw import random import json from pathlib import Path# 创建一个黑色背景图像 width, height 5000, 5000 # 图像宽度和高度 background_color (0, 0, 0) # 黑色填充# 随机分布图像 num_images 1 # …...

最小化安装移动云大云操作系统--BCLinux-for-Euler-22.10-everything-x86_64-230316版
CentOS 结束技术支持,转为RHEL的前置stream版本后,国内开源Linux服务器OS生态转向了开源龙蜥和开源欧拉两大开源社区,对应衍生出了一系列商用Linux服务器系统。BCLinux-for-Euler-22.10是中国移动基于开源欧拉操作系统22.03社区版本深度定制的…...

003传统图机器学习、图特征工程
文章目录 一. 人工特征工程、连接特征二. 在节点层面对连接特征进行特征提取三. 在连接层面对连接特征进行特征提取四. 在全图层面对连接特征进行特征提取 一. 人工特征工程、连接特征 节点、连接、子图、全图都有各自的属性特征, 属性特征一般是多模态的。除属性特…...
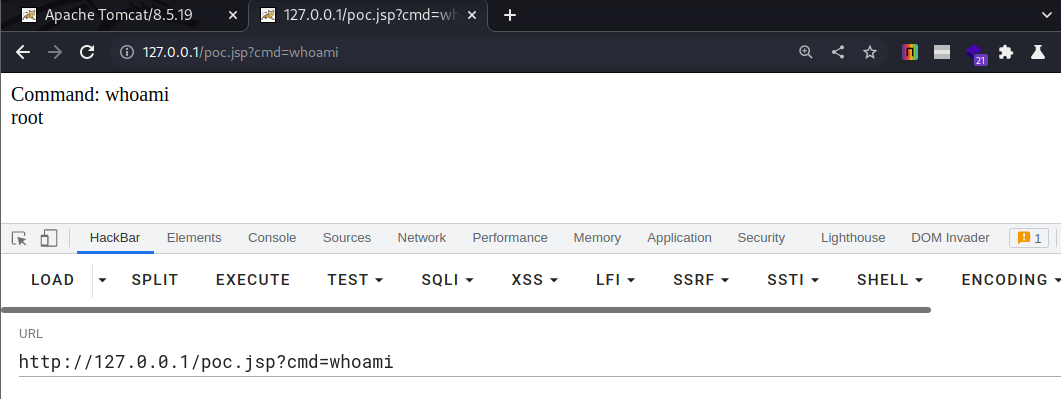
Apache Tomcat 漏洞复现
文章目录 Apache Tomcat 漏洞复现1. Tomcat7 弱密码和后端 Getshell 漏洞1.1 漏洞描述1.2 漏洞复现1.3 漏洞利用1.3.1 jsp小马1.3.2 jsp大马 1.4 安全加固 2. Aapache Tomcat AJP任意文件读取/包含漏洞2.1 漏洞描述2.1 漏洞复现2.2 漏洞利用工具2.4 修复建议 3. 通过 PUT 方法的…...

Oracle-常用权限-完整版
-- 创建用户 create user TCK identified by oracle; -- 赋权 grant connect,resource to TCK; -- 删除权限 revoke select any table from TCK -- 删除用户 CASCADE(用户下的数据级联删除) drop user TCK CASCADE -- 查询权限列表 select * from user_role_privs; select * fr…...
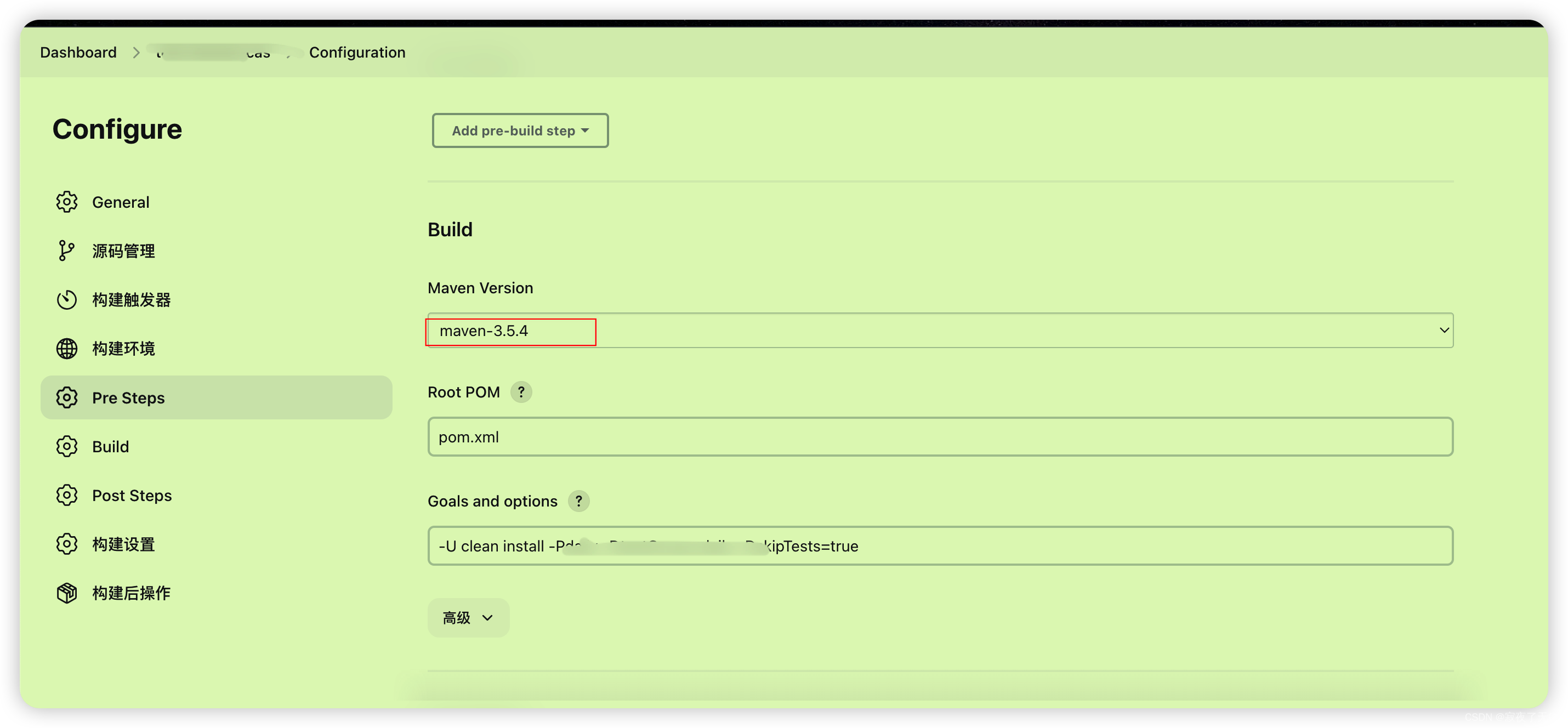
jenkins 发布job切换不同的jdk版本/ maven版本
1. 技术要求 因为有个新的项目需要使用jdk17 而旧的项目需要jdk1.8 这就需要jenkins在发布项目的时候可以指定jdk版本 2. 解决 jenkins全局工具配置页面 配置新的jdk 路径 系统管理-> 全局工具配置 如上新增个jdk 名称叫 jdk-17 然后配置jdk-17的根路径即可(这…...
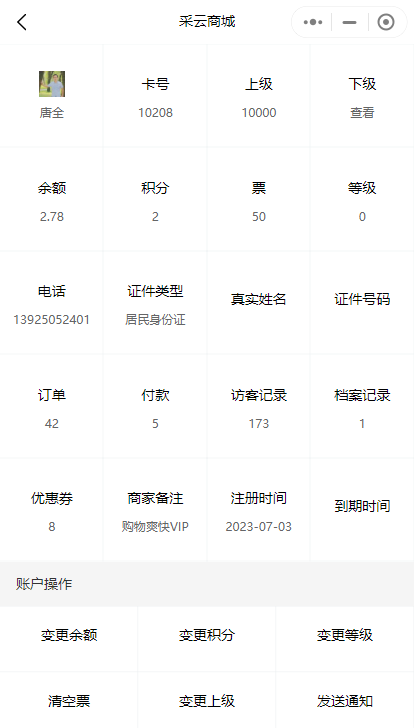
如何在小程序中给会员设置备注
给会员设置备注是一项非常有用的功能,它可以帮助商家更好地管理和了解自己的会员。下面是一个简单的教程,告诉商家如何在小程序中给会员设置备注。 1. 找到指定的会员卡。在管理员后台->会员管理处,找到需要设置备注的会员卡。也支持对会…...
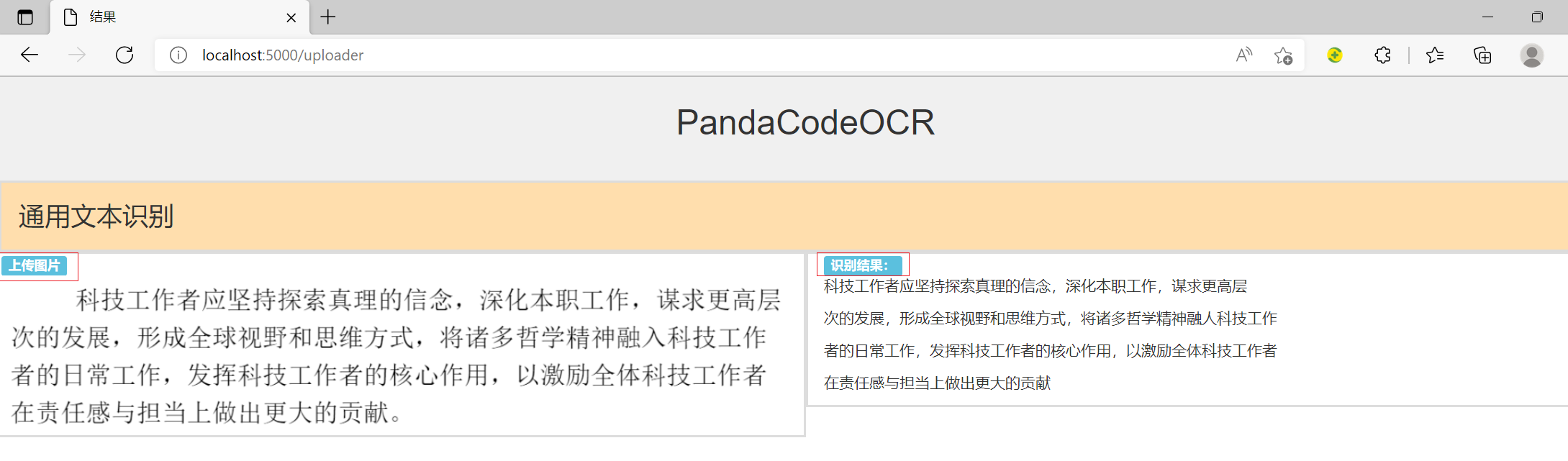
PaddleOCR学习笔记2-初步识别服务
今天初步实现了网页,上传图片,识别显示结果到页面的服务。后续再完善。 采用flask paddleocr bootstrap快速搭建OCR识别服务。 代码结构如下: 模板页面代码文件如下: upload.html : <!DOCTYPE html> <html> <…...

【Opencv】Pyhton 播放上一帧,下一帧,存video,逐帧分析
文章目录 读取具体哪一帧等待按钮写入解码方式与文件格式对应全部代码 读取具体哪一帧 这个方法可以获取某一帧: while True:cap.set(cv2.CAP_PROP_POS_FRAMES, current_frame)ret, frame cap.read()if not ret:break等待按钮 这个方法可以显示当前帧,…...
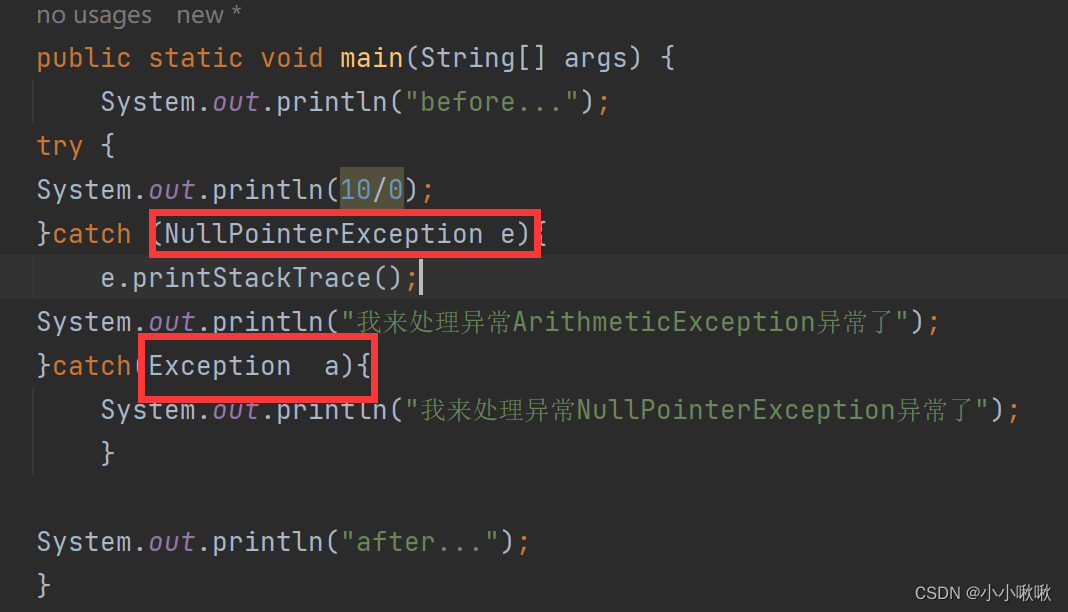
【关于Java:认识异常】
文章目录 一、1. 异常概念与体系结构1.1 异常的概念1.2 常见的异常1.算数异常2.数组越界异常3.空指针异常 1.3 异常的体系结构1.4 异常的分类1. 编译时异常2. 运行时异常(RuntimeException) 二、 异常的处理方式2.1 防御式编程2.2 EAFP:(异常…...

【C++ • STL • 力扣】详解string相关OJ
文章目录 1、仅仅翻转字母2、字符串中的第一个唯一字符3、字符串里最后一个单词的长度4、验证一个字符串是否是回文5、字符串相加总结 ヾ(๑╹◡╹)ノ" 人总要为过去的懒惰而付出代价 ヾ(๑╹◡╹)ノ" 1、仅仅翻转字母 力扣链接 代码1展示&…...
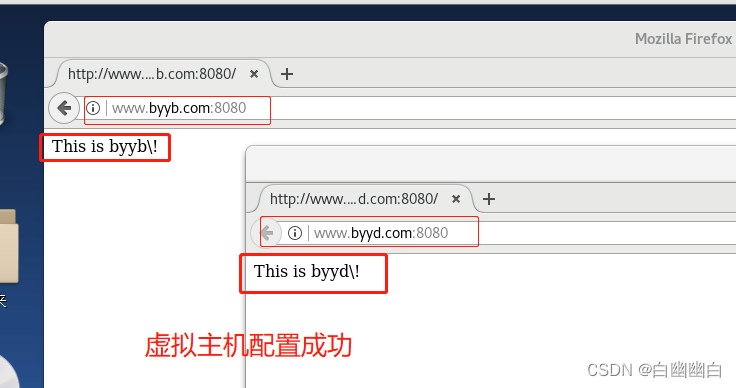
【Tomcat服务部署及优化】
Tomcat 一、什么是Tomcat?二、Tomcat 核心组件2.1 Tomcat 组件2.3 Container组件的结构2.4 Tomcat 请求过程 三、Tomcat 部署3.1 安装JDK3.2 设置JDK环境变量3.3 安装Tomcat并用supervisor启动解压添加到supervisord服务测试能否通过supervisorctl启动 四、Tomcat的端口和主要…...
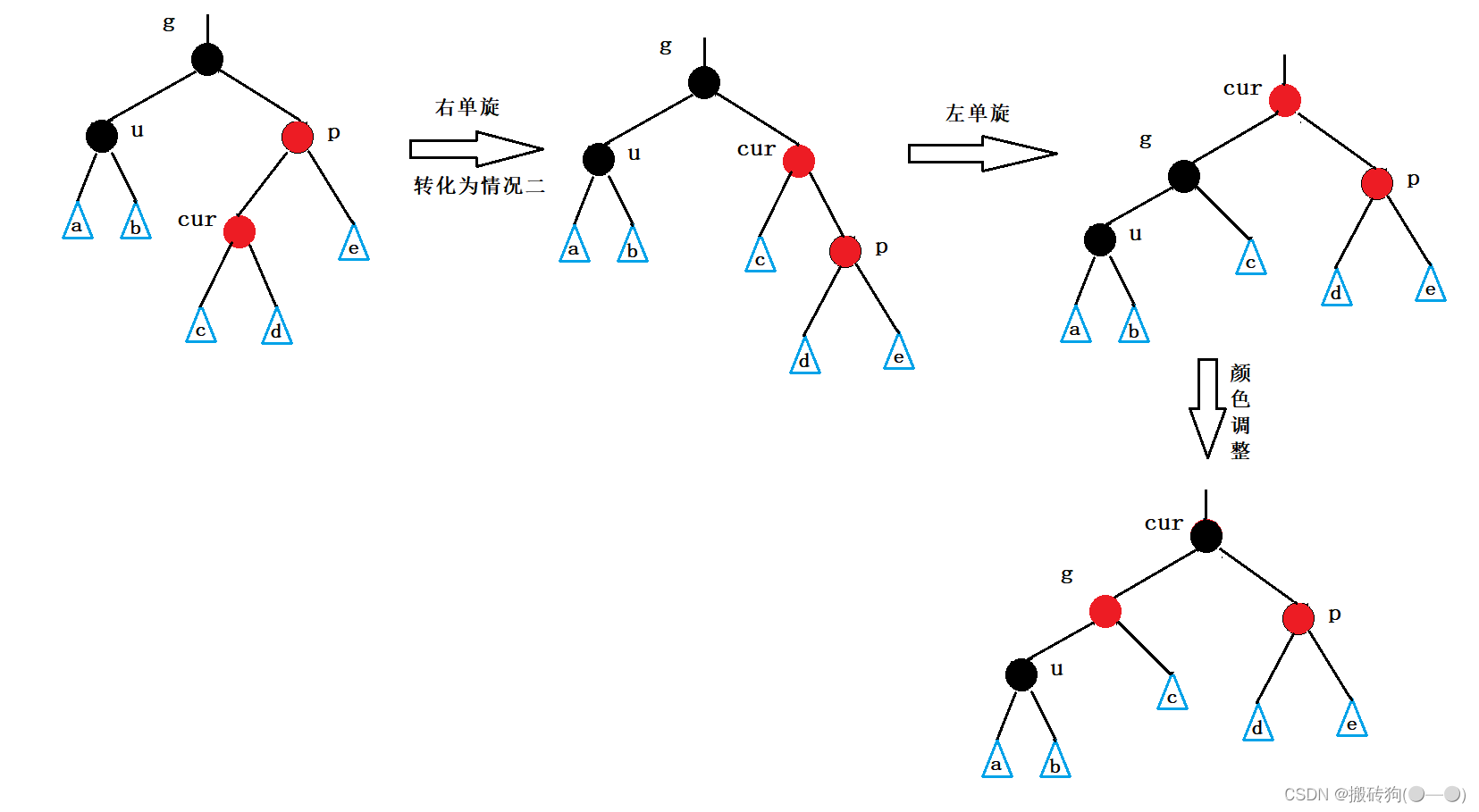
C++之红黑树
红黑树 红黑树的概念红黑树的性质红黑树结点的定义红黑树的插入红黑树的验证红黑树与AVL树的比较 红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上…...
TCP)
Go语言网络编程(socket编程)TCP
1、TCP编程 1.1.1 Go语言实现TCP通信 TCP协议 TCP/IP(Transmission Control Protocol/Internet Protocol) 即传输控制协议/网间协议,是一种面向连接(连接导向)的、可靠的、基于字节流的传输层(Transport layer)通信协…...

C语言——局部和全局变量
局部变量 定义在函数内部的变量称为局部变量(Local Variable) 局部变量的作用域(作用范围)仅限于函数内部, 离开该函数后是无效的 离开该函数后,局部变量自动释放 示例代码: #include <stdio.h>// 函数定义 …...
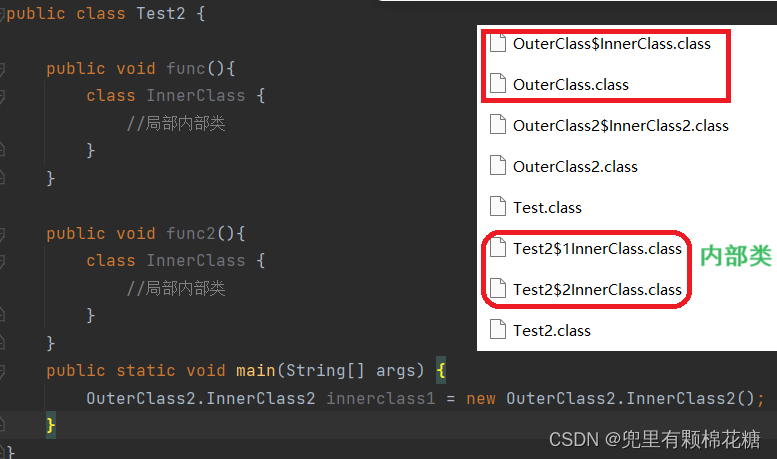
【Java基础篇 | 类和对象】--- 聊聊什么是内部类
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【JavaSE_primary】 本专栏旨在分享学习Java的一点学习心得,欢迎大家在评论区讨论💌 前言 当一个事物的内部&…...

合宙Air724UG LuatOS-Air LVGL API控件-页面 (Page)
页面 (Page) 当控件内容过多,无法在屏幕内完整显示时,可让其在 页面 内显示。 示例代码 page lvgl.page_create(lvgl.scr_act(), nil) lvgl.obj_set_size(page, 150, 200) lvgl.obj_align(page, nil, lvgl.ALIGN_CENTER, 0, 0)label lvgl.label_crea…...
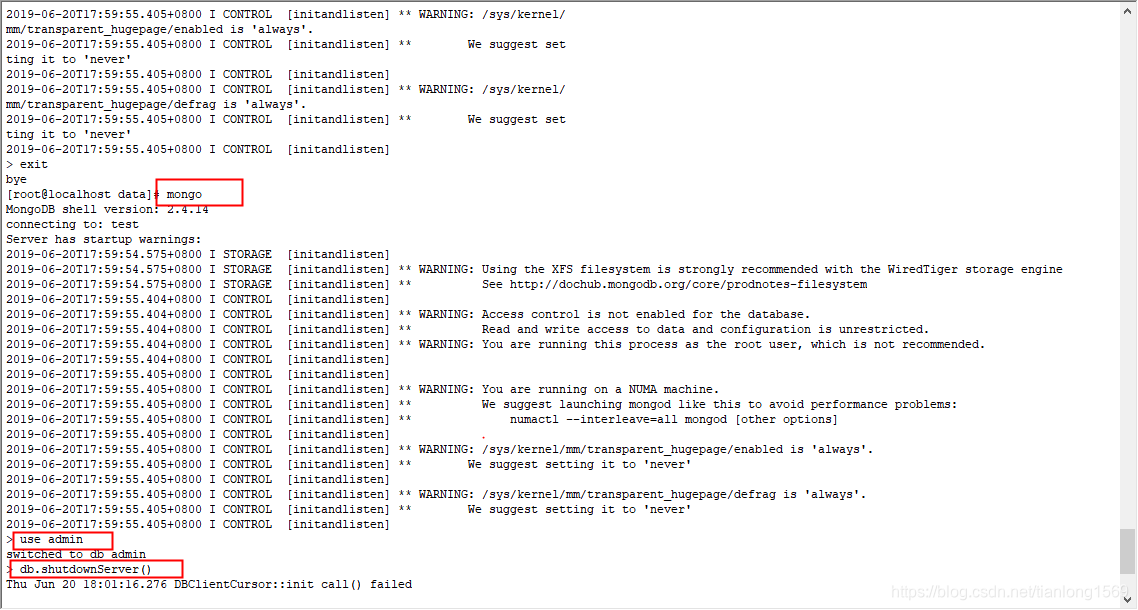
mongodb数据库操作
1、启动mongodb /usr/local/mongodb/bin/mongod --dbpath /var/mongodb/data/--logpath /var/mongodb/logs/log.log &在mongodb启动命令中 --dbpath 指定mongodb的数据存储路径 --logpath 指定mongodb的日志存储路径 2、停止mongodb 第一步先进入mongo命令行模式 第二…...
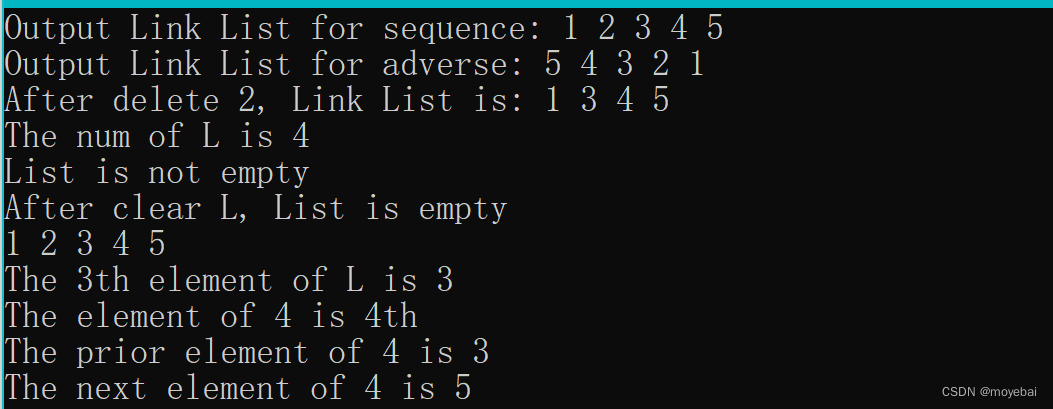
第 2 章 线性表 ( 双链循环线性表(链式存储结构)实现)
1. 背景说明 2. 示例代码 1) status.h /* DataStructure 预定义常量和类型头文件 */#ifndef STATUS_H #define STATUS_H#define CHECK_NULL(pointer) if (!(pointer)) { \printf("FuncName: %-15s Line: %-5d ErrorCode: %-3d\n", __func__, __LINE__, ERR_NULL_PTR…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
