【C++进阶】:AVL树(平衡因子)
AVL树
- 一.概念
- 二.插入
- 1.搜索二叉树
- 2.平衡因子
- 三.旋转
- 1.更新平衡因子
- 2.旋转
- 1.左单旋
- 2.右单旋
- 3.先右旋再左旋
- 4.先左旋再右旋
- 四.完整代码
一.概念
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
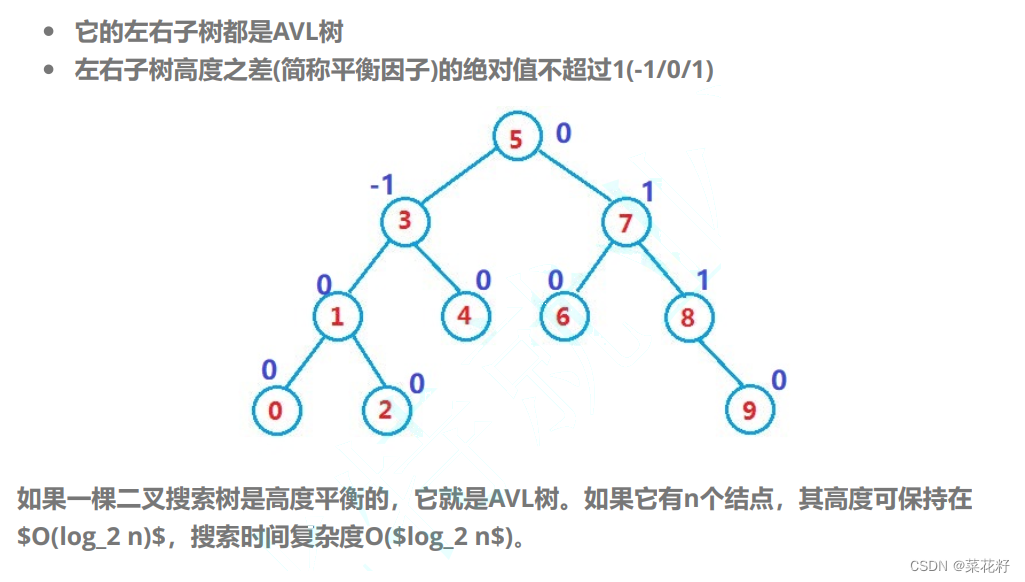
二.插入
AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。那么AVL树的插入过程可以分为两步:
- 按照二叉搜索树的方式插入新节点
- 调整节点的平衡因子
1.搜索二叉树
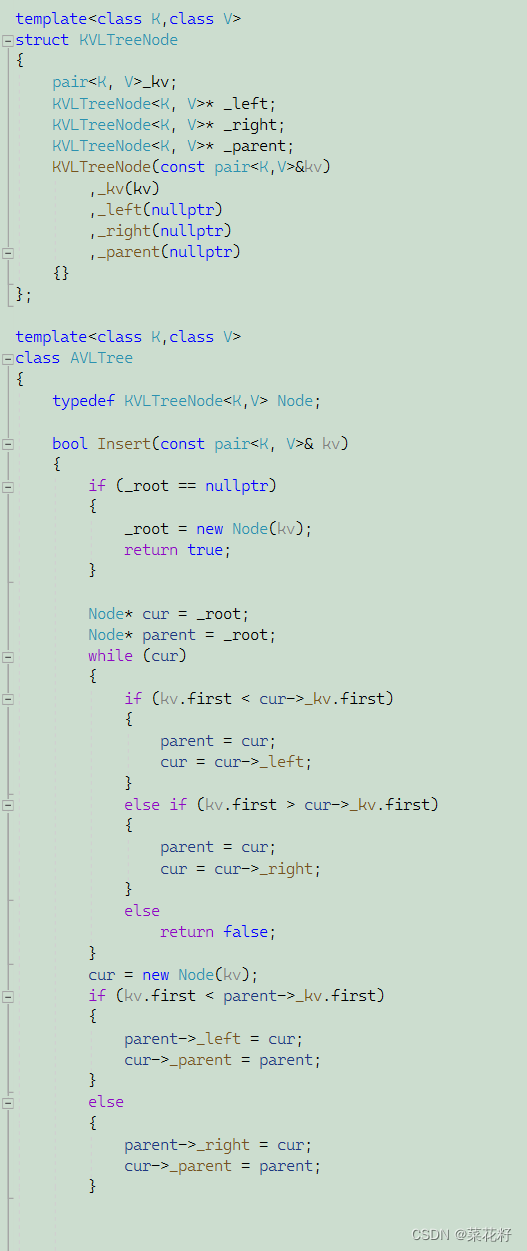
2.平衡因子
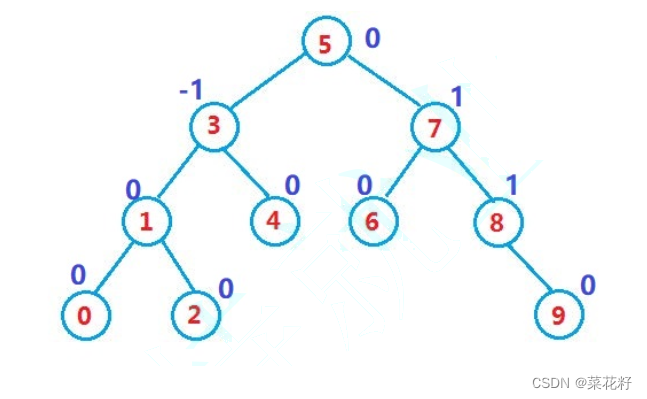
一颗树如何插入会影响节点的平衡因子呢?(平衡因子是右节点减去左节点)
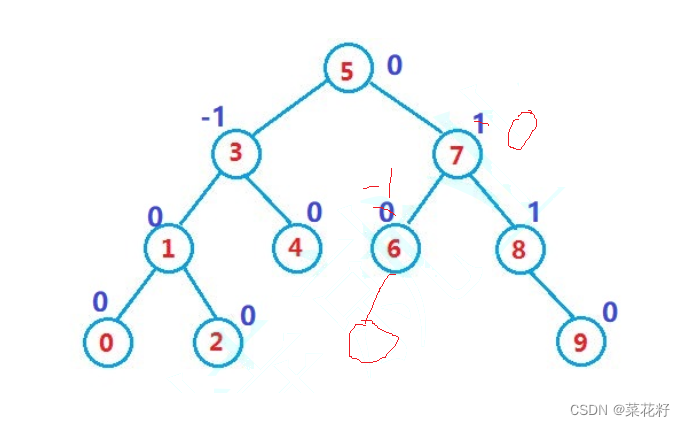
如果我们插在6的左边,那么6的平衡因子减一,同理7的左子树高度加一,那么7的平衡因子减一,再继续向上5的右子树的最高高度并没有发生改变,所以5的平衡因子不发生改变。
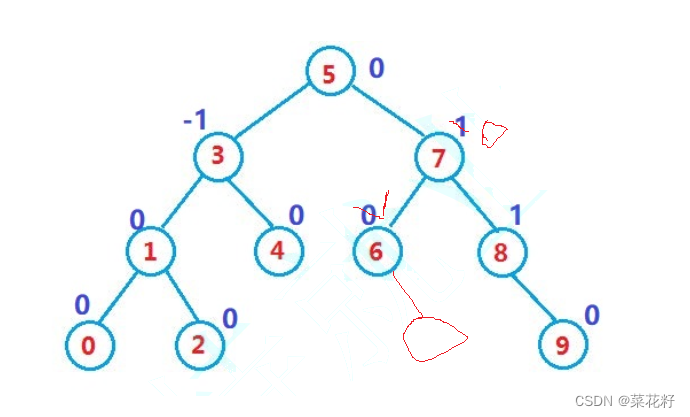
同理,插在6的右边,6的平衡因子加一,7的平衡因子减一。

如果插在9的右边,那么8的平衡因子就会变为2,说明此树不平衡。
总结:
1.新镇在左,parent平衡因子减减。
2.新增在右,parent平衡因子加加。
3.如果更新后的parent平衡因子为0,说明parent所在的树的高度不变,不会再影响祖先,不用再继续更新了。
4如果更新后parent的平衡因子为1或者-1,那么就需要继续向上更新。
5.如果更新后,parent平衡因子为2或-2,说明该树不平衡,对parent所在的子树进行旋转。
三.旋转
1.更新平衡因子
由上面分析可以知道更新结束的条件是平衡因子为0或者更新到根节点。
首先在每个节点里加入平衡因子

接着在插入的同时更新平衡因子

2.旋转
旋转要保持的要求:
1.旋转后也是搜索二叉树。
2.变成平衡树并且降低树的高度。
如果在一棵原本是平衡的AVL树中插入一个新节点,可能造成不平衡,此时必须调整树的结构,使之平衡化。根据节点插入位置的不同,AVL树的旋转分为四种:
1.左单旋
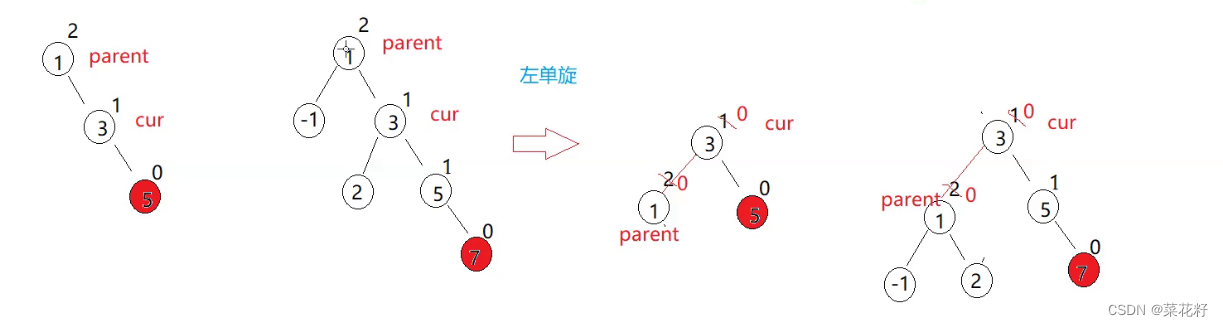

通过观察我们可以发现,我们其实只需要移动蓝色的节点就可以实现左旋。我们将这三个节点分别记录,然后修改它们的内部属性即可。
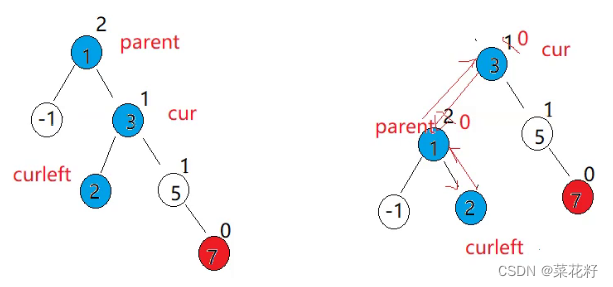

2.右单旋
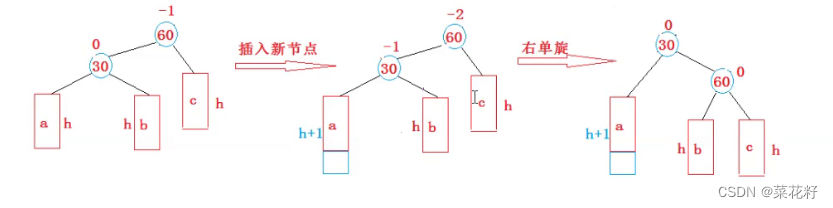

3.先右旋再左旋
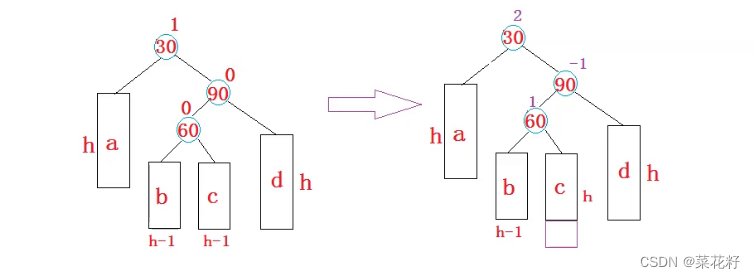
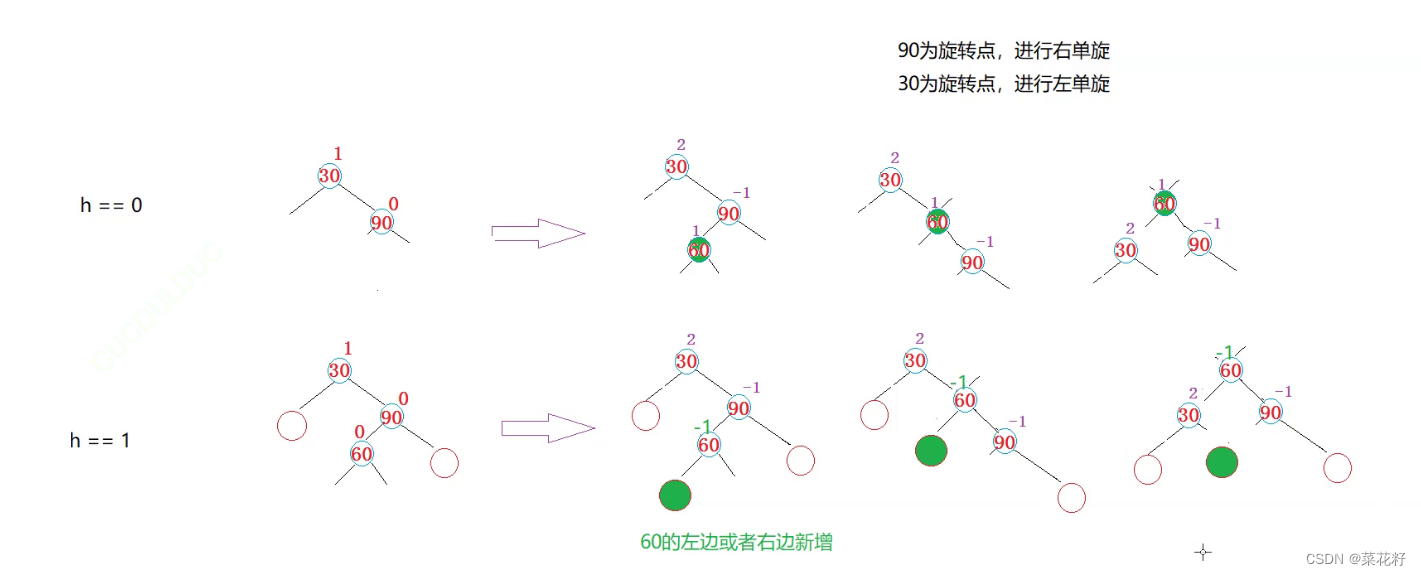
这里的旋转并不难,直接复用就可以.

困难的部分是如何调控平衡因子,插入的位置不同,平衡因子也不同分三种情况讨论。
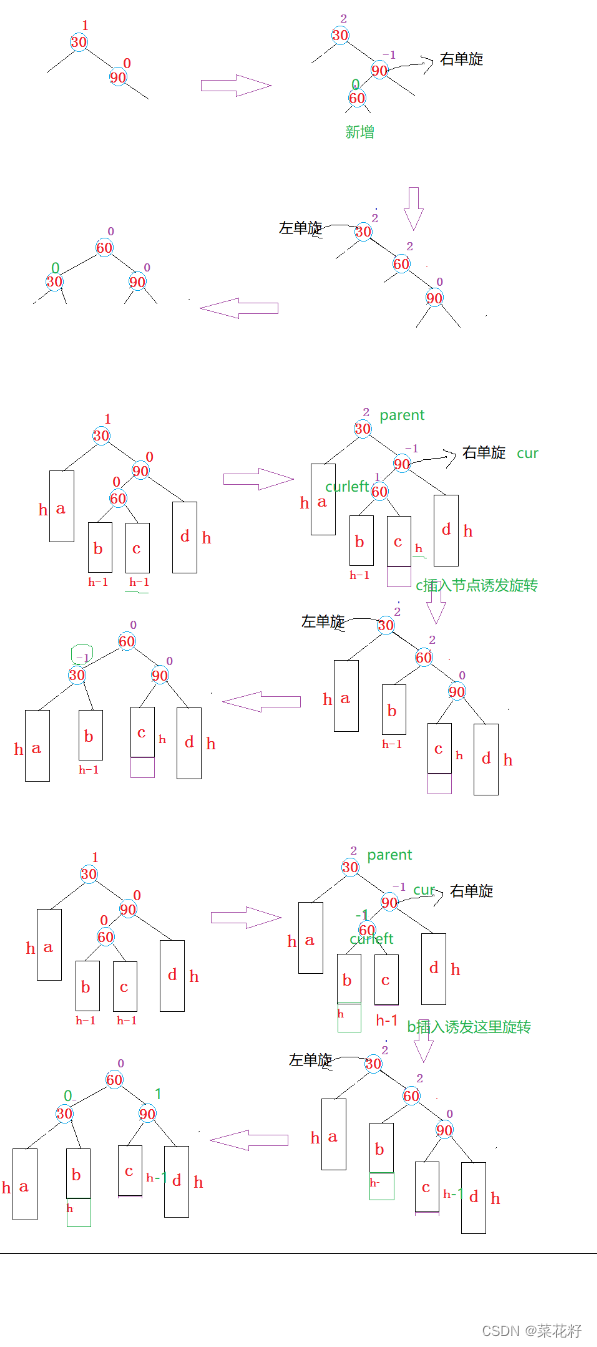

4.先左旋再右旋
同理,左右旋与上文一样,需要分三种情况来讨论。
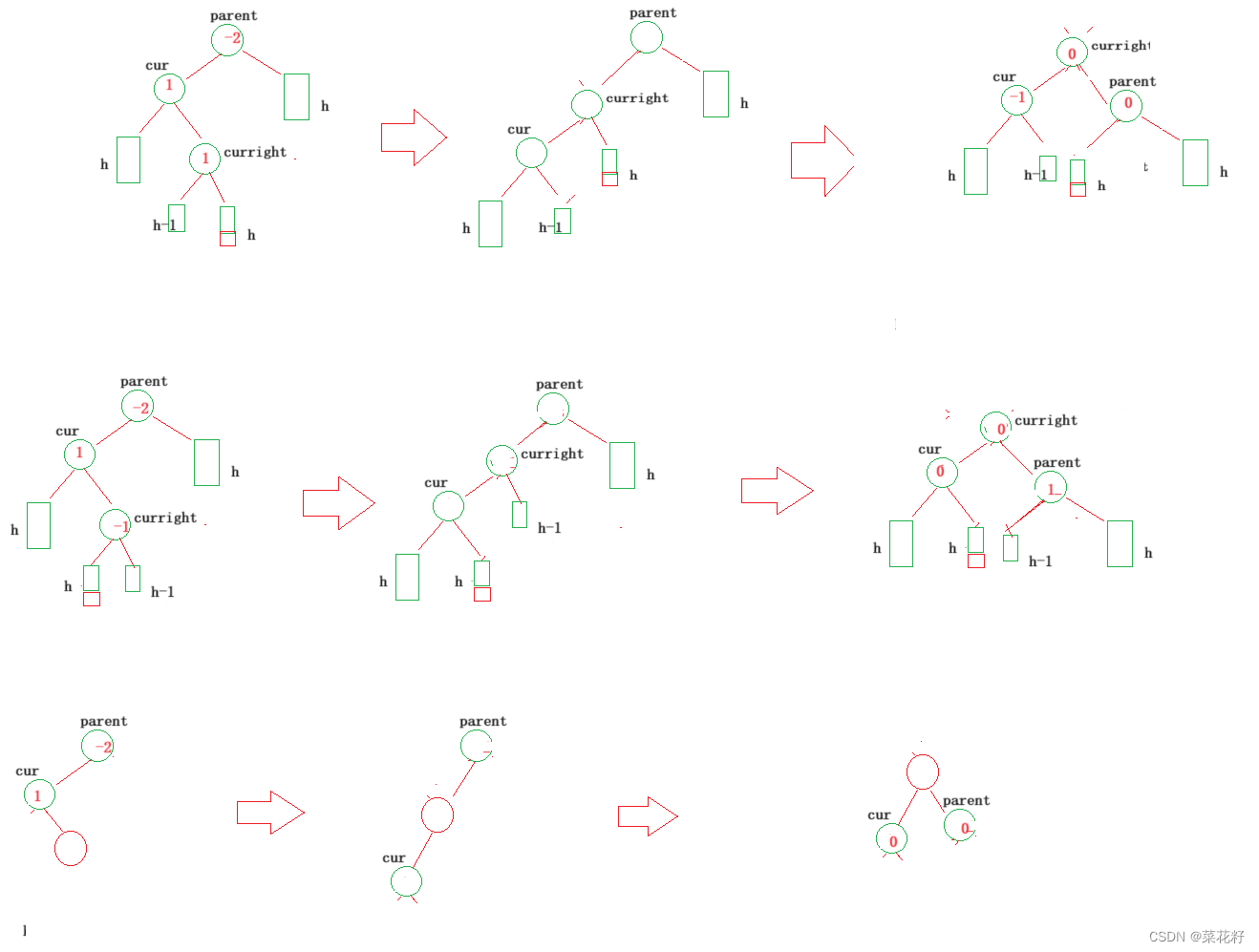

四.完整代码
测试
#include"KVL.h"
#include<vector>int main()
{AVLTree<int,int> t;srand(time(0));vector<int>a;for (int i = 0; i < 100; i++)a.push_back(rand());for (auto x : a)t.Insert(make_pair(x,x));t.Print();
}
树
#include<iostream>
#include<assert.h>
using namespace std;template<class K,class V>
struct KVLTreeNode
{pair<K, V>_kv;KVLTreeNode<K, V>* _left;KVLTreeNode<K, V>* _right;KVLTreeNode<K, V>* _parent;int _bf;//平衡因子KVLTreeNode(const pair<K,V>&kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};template<class K,class V>
class AVLTree
{
public:typedef KVLTreeNode<K,V> Node;bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = _root;while (cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}elsereturn false;}cur = new Node(kv);if (kv.first < parent->_kv.first){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}//控制平衡while (parent){if (cur == parent->_left){parent->_bf--;}else // if (cur == parent->_right){parent->_bf++;}if (parent->_bf == 0){// 更新结束break;}else if (parent->_bf == 1 || parent->_bf == -1){// 继续往上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){// 子树不平衡了,需要左旋转if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}//右旋转else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}//先左单旋再右旋转else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}//先右单选再左单旋else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}break;}else{assert(false);}}return true;}void RotateL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;Node* ppnode = parent->_parent;//记录父节点的父节点//父节点的右孩子变成curleftparent->_right = curleft;if(curleft)//细节注意curleft为空时不能操作curleft->_parent = parent;//父节点变为cur的左孩子cur->_left = parent;parent->_parent = cur;//如果原来父节点是根节点if (parent == _root){_root = cur;cur->_parent = nullptr;}else//如果不是根节点判断它应该是左儿子还是右儿子{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;}void RotateR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;Node* pphead = parent->_parent;//父节点到cur右边cur->_right=parent;parent->_parent = cur;//父节点的左孩子变成currightparent->_left = curright;if (curright)curright->_parent = parent;//cur的父节点变为原来父节点的父节点if (pphead)//如果不是根节点{if (pphead->_left == parent)pphead->_left = cur;elsepphead->_right = cur;cur->_parent = pphead;}else{_root = cur;cur->_parent = nullptr;}parent->_bf = cur->_bf = 0;}void RotateRL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;int bf = curleft->_bf;RotateR(parent->_right);RotateL(parent);//第一种情况if (bf == 0){parent->_bf = cur->_bf = 0;}//第二种情况else if (bf == 1){parent->_bf = -1, cur->_bf = 0, curleft->_bf = 0;}//第三种情况else if(bf==-1){cur->_bf = 1, curleft->_bf = 0, parent->_bf = 0;}//其他情况错误else{assert(false);}}void RotateLR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){parent->_bf = cur->_bf = 0;}else if (bf == 1){parent->_bf = curright->_bf = 0, cur->_bf = -1;}else if (bf == -1){parent->_bf = 1, cur->_bf = curright->_bf = 0;}else{assert(false);}}void Print(){Print(_root);}void Print(Node* root){if (root == nullptr) return;Print(root->_left);cout << root->_kv.second << ' ';Print(root->_right);}
private:Node* _root=nullptr;
};
相关文章:

【C++进阶】:AVL树(平衡因子)
AVL树 一.概念二.插入1.搜索二叉树2.平衡因子 三.旋转1.更新平衡因子2.旋转1.左单旋2.右单旋3.先右旋再左旋4.先左旋再右旋 四.完整代码 一.概念 二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元…...
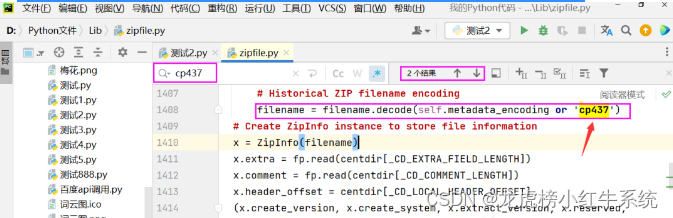
Python教程33:关于在使用zipfile模块,出现中文乱码的解决办法
zipfile是Python标准库中的一个模块,zipfile里有两个class, 分别是ZipFile和ZipInfo,用来创建和读取zip文件,而ZipInfo是存储的zip文件的每个文件的信息的。ZIP文件是一种常见的存档文件格式,它可以将多个文件和目录压缩为一个文件…...
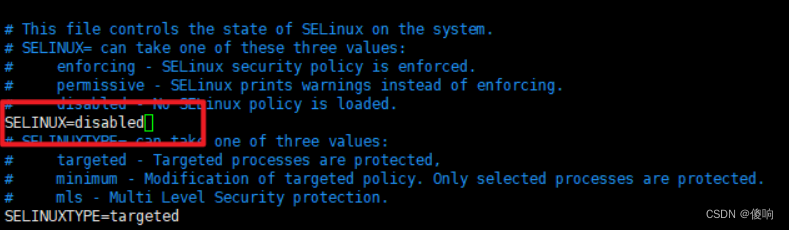
【疑难杂症】使用xshell连接云服务器连接不上
目录 【1】使用xshell连接云服务器连接不上 【1.1】解决方法一 【1.2】解决方法二 【1】使用xshell连接云服务器连接不上 Centos7使用xshell连接提示"ssh服务器拒绝了密码 请再试一次"。 问题如图所示,新安装了一台Centos7服务器,使用ssh连…...

Qt MinGW / MSVC
MinGW/MSVC的关系 MinGW / MSVC.dll / .lib / .a 的关系 MinGW / MSVC Qt 中有两种方式编译:一种是MinGW ,另一种MSVC,是两种不同的编译器。 MinGW(Minimalist GNUfor Windows),它是一个可自由使用和自由发布的Windows特定头文件…...

【数学建模】数据预处理
为什么需要数据预处理 数学建模是将实际问题转化为数学模型来解决的过程,而数据预处理是数学建模中非常重要的一步。以下是为什么要进行数据预处理的几个原因: 数据质量:原始数据往往存在噪声、异常值、缺失值等问题,这些问题会对…...
VMware 安装 黑群晖7.1.1-42962 DS918+
本例的用的文件 1、ARPL 1.0beat 引导文件 vmdk格式: https://download.csdn.net/download/mshxuyi/88309308 2、DS918_42962.pat:https://download.csdn.net/download/mshxuyi/88309383 一、引导文件 1、创建一个虚拟机 2、下一步,选稍后…...
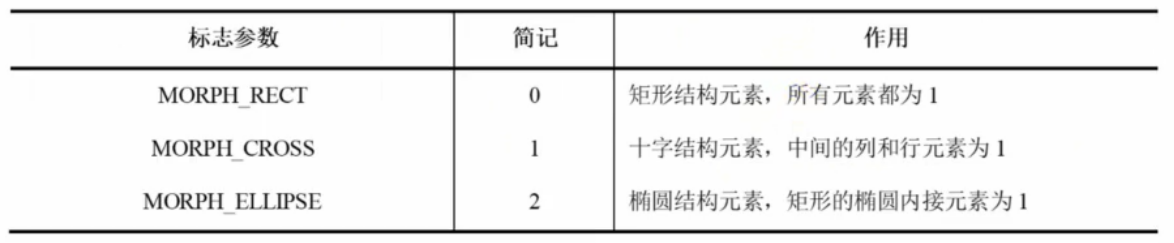
OpenCV(二十九):图像腐蚀
1.图像腐蚀原理 腐蚀操作的原理是将一个结构元素(也称为核或模板)在图像上滑动,并将其与图像中对应位置的像素进行比较。如果结构元素的所有像素与图像中对应位置的像素都匹配,那么该位置的像素值保持不变。如果结构元素的任何一个…...
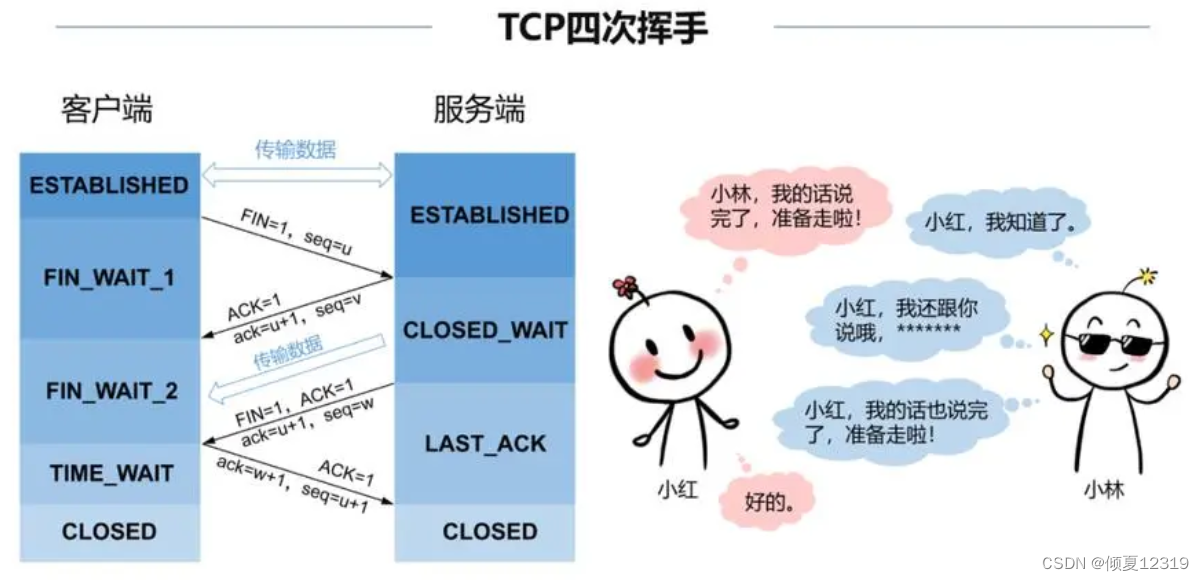
【网络知识点】三次握手和四次挥手
文章目录 一、三次握手二、四次挥手 一、三次握手 三次握手的原理如下: 客户端向服务器发送一个SYN(同步)包,其中包含一个随机生成的初始序列号(ISN)。 服务器收到SYN包后,会发送一个SYNACK&…...

CSS整理
目录 CSS中的& 弹性(display:flex)布局 flex的对齐方式 justify-content align-items flex-wrap 弹性盒换行 flex:1 flex属性 flex-grow:项目的放大比例 flex-shrink:收缩 flex-basis:初始值ÿ…...

OpenCV 06(图像的基本变换)
一、图像的基本变换 1.1 图像的放大与缩小 - resize(src, dsize, dst, fx, fy, interpolation) - src: 要缩放的图片 - dsize: 缩放之后的图片大小, 元组和列表表示均可. - dst: 可选参数, 缩放之后的输出图片 - fx, fy: x轴和y轴的缩放比, 即宽度和高度的缩放比. - …...

Java 中的日期时间总结
前言 大家好,我是 god23bin,在日常开发中,我们经常需要处理日期和时间,日期和时间可以说是一定会用到的,现在总结下 Java 中日期与时间的基本概念与一些常用的用法。 基本概念 日期(年月日,某…...
创建10个线程并发执行(STL/Windows/Linux)
C并发编程入门 目录 STL 写法 #include <thread> #include <iostream> using namespace std;void thread_fun(int arg) {cout << "one STL thread " << arg << " !" << endl; }int main(void) {int thread_count 1…...

三、创建各个展示模块组件
简介 在文件 components 中创建轮播模块组件,引入App.vue展示。欢迎访问个人的简历网站预览效果 本章涉及修改与新增的文件:First.vue、Second.vue、Third.vue、Fourth.vue、Fifth.vue、App.vue、vite-env.d.ts、assets 一、修改vite-env.d.ts文件 /// <reference type…...

推荐一款程序员截图神器!
快来看一下程序员必备的一款截图工具 今天就来和大家说一下作为程序员必备截图神器,几乎每一个程序员都会设置开机自启,因为这个截图功能太太太好用了!!!只要你在键盘上按下F1就可以轻松截取整个屏幕,然后…...

无涯教程-JavaScript - IMCSC函数
描述 IMCSC函数以x yi或x yj文本格式返回复数的余割。 复数的余割定义为正弦的倒数。即 余割(z) 1 /正弦(z) 语法 IMCSC (inumber)争论 Argument描述Required/OptionalInumberA complex number for which you want the cosecant.Required Notes Excel中的复数只是简单…...

Ubuntu22.04 LTS 显卡相关命令
第一部分查看驱显卡信息 一、查看显卡型号 # -i表示不区分大小写 lspci | grep -i nvidia # 必须安装好nvidia驱动 nvidia-smi -L 二、查看显卡驱动版本 cat /proc/driver/nvidia/version 三、查看CUDA、cuDNN版本 # 或者 nvcc -V(两个显示的版本一致…...

《TCP/IP网络编程》阅读笔记--基于 TCP 的半关闭
目录 1--基于TCP的半关闭 1-1--TCP单方面完全断开的问题 1-2--shutdown()函数 1-3--半关闭的必要性 2--基于半关闭的文件传输程序 1--基于TCP的半关闭 1-1--TCP单方面完全断开的问题 Linux 系统中的 close 函数会将 TCP Socket 的连接完全断开,这意味着不能收…...

Rust的模块化
Rust的模块化要从Rust的入口文件谈起。 Rust的程序的入口文件有两个 如果程序类型是可执行应用,入口文件是main.rs;如果程序类型是库,入口文件是lib.rs; 入口文件中,必须声明本地模块,否则编译器在编译过…...

vmware设置桥接模式后ip设置
网络连接方式设置 找到虚拟机里机器的网络设置 左边是宿主机,右边是虚拟机,按照这个设置就可以上网了(IP指定一个没有占用的值,子网掩码和网关设置成一样的)就可以联网了。 over~~...
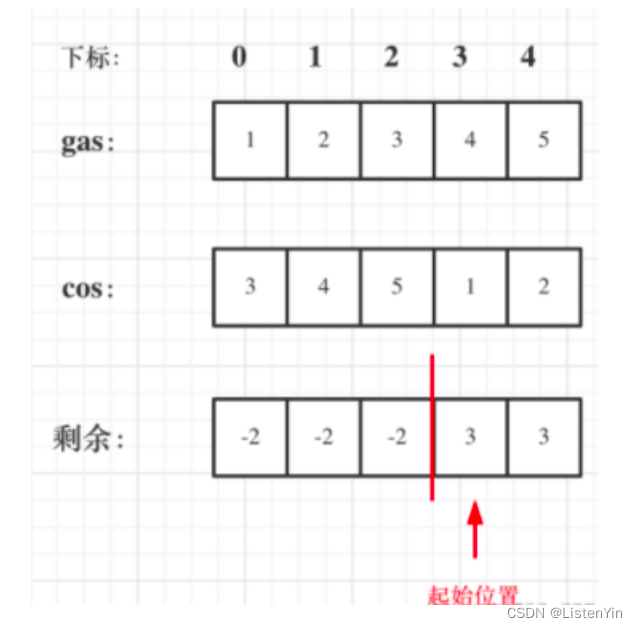
算法通关村第十七关:白银挑战-贪心高频问题
白银挑战-贪心高频问题 1. 区间问题 所有的区间问题,参考下面这张图 1.1 判断区间是否重叠 LeetCode252 https://leetcode.cn/problems/meeting-rooms/ 思路分析 因为一个人在同一时刻只能参加一个会议,因此题目的本质是判断是否存在重叠区间 将区…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...
