递推算法及常见示例(C++、Python实现)
递推算法及常见示例(C++、Python实现)
递推算法是一种用若干步可重复运算来描述复杂问题的方法,它是一种序列计算中的常用算法。通常是通过计算前面的一些项来得出序列中的指定项的值。其思想是把一个复杂的庞大的计算过程转化为简单过程的多次重复,该算法利用了计算机速度快和不知疲倦的机器特点。递推关系通常表示为一种递推公式。
下面是一些常见的例子。
★斐波那契数列:斐波那契数列指的是这样一个数列:0,1,1,2,3,5,8,13,21,34,55,89...
这个数列从第3项开始,每一项都等于前两项之和。
斐波那契数列是一种经典的递推问题,它的定义是:f(0)=0,f(1)=1,f(n)=f(n-1)+f(n-2)。通过这个递推关系式,可以求解斐波那契数列的第 n 项。
☆C++实现:
#include <iostream>
using namespace std; int main() { int n; cout << "请输入项数 n 的值: "; cin >> n; if (n <= 1) { return n; } int f1 = 0, f2 = 1, fn; for (int i = 2; i <= n; i++) { fn = f1 + f2; f1 = f2; f2 = fn; } cout << "斐波那契数列的第 " << n << " 项为:" << fn << endl; return 0;
}
下面改用使用自定义函数实现:
#include <iostream>
using namespace std; int fibonacci(int n) { if (n <= 1) { return n; } int f1 = 0, f2 = 1, fn; for (int i = 2; i <= n; i++) { fn = f1 + f2; f1 = f2; f2 = fn; } return fn;
} int main() { int n; cout << "请输入项数 n 的值: "; cin >> n; cout << "斐波那契数列的第 " << n << " 项为:" << fibonacci(n) << endl; return 0;
}
☆Python实现:
n = int(input("请输入 n 的值:"))
if n <= 1: fn = nf1, f2 = 0, 1 for i in range(2, n+1): fn = f1 + f2 f1, f2 = f2, fnprint("斐波那契数列的第 {} 项为:{}".format(n, fn))
下面改用使用自定义函数实现:
def fibonacci(n): if n <= 1: return nf1, f2 = 0, 1 for i in range(2, n+1): fn = f1 + f2 f1, f2 = f2, fn return fn n = int(input("请输入 n 的值:"))
print("斐波那契数列的第 {} 项为:{}".format(n, fibonacci(n)))
★等差数列求和: 1, 3, 5, 7, 9 是一个公差为 2 的等差数列。等差数列的求和问题可以通过递推算法解决。设等差数列的首项为 a1,公差为 d,第 n 项为 an,则 an=a1+(n-1)d。要求等差数列的前 n 项和,可以递推得到:Sn=a1+a2+...+an=n/2[2a1+(n-1)d]。
☆C++实现:
#include <iostream>
using namespace std;int main() { int a1, d, n; cout << "输入第一项、公差和项数:"; cin >> a1 >> d >> n; int sum = 0; for (int i = 1; i <= n; i++) { sum += a1 + (i - 1) * d; } cout << "等差数列的前 " << n << " 项和为:" << sum << endl; return 0;
}
☆Python实现:
a1 = int(input("输入第一项: "))
d = int(input("输入公差: "))
n = int(input("输入项数: "))
sum = 0
for i in range(1, n+1): sum += a1 + (i - 1) * dprint("等差数列的前 {} 项和为:{}".format(n,sum))★等比数列求和:1, 2, 4, 8, 16 是一个公比为 2 的等比数列。等比数列的求和问题也可以通过递推算法解决。设等比数列的首项为 a1,公比为 r,第 n 项为 an,则 an=a1r^(n-1)。要求等比数列的前 n 项和,可以递推得到:Sn=a1(1-r^n)/(1-r)。
☆C++实现:
#include <iostream>
#include <cmath> // 引入 pow()
using namespace std;int main() { double a1, r, n; cout << "输入第一项、公比和项数:"; cin >> a1 >> r >> n; double sum = 0; for (int i = 1; i <= n; i++) { sum += a1 * pow(r, i - 1); } cout << "等比数列的前 " << n << " 项和为:" << sum << endl; return 0;
}
☆Python实现:
a1 = float(input("输入第一项:"))
r = float(input("输入公比:"))
n = int(input("输入项数:")) sum = 0
for i in range(1, n + 1): sum += a1 * (r ** (i - 1)) print("等比数列的前 {} 项和为:{}".format(n, sum))
附、递推、递归和迭代区别
递推是通过已知序列元素来计算其他元素,递归是函数调用自身,迭代是通过重复执行操作来解决问题。
递归和迭代可参见:https://blog.csdn.net/cnds123/article/details/132409886
相关文章:
)
递推算法及常见示例(C++、Python实现)
递推算法及常见示例(C、Python实现) 递推算法是一种用若干步可重复运算来描述复杂问题的方法,它是一种序列计算中的常用算法。通常是通过计算前面的一些项来得出序列中的指定项的值。其思想是把一个复杂的庞大的计算过程转化为简单过程的多次…...
vscode调试程序设置
主要设置和json内容如下: cpp_properties.json内容: {"configurations": [ //C intellisense插件需要这个文件,主要是用于函数变量等符号的只能解析{"name": "Win32","includePath": ["${work…...
电商邮件营销攻略:教你如何有效运营邮件营销策略!
作为一种领先的营销渠道,电子邮件营销已被电子商务公司作为推动客户参与度、促进销售和提高ROI的不可或缺的方式。在这篇文章中,我们将深入探讨电子商务公司为什么要做EDM邮件营销?以及电商公司怎么做邮件营销? 一、电子商务公司…...
centos+jenkins+pycharm
思路:架构 一. 在centos上搭建jenkins环境 二. pycharm与gitee建立连接 三. 访问jenkins,添加任务 3.1 添加一个自由风格的任务 3.2 添加git项目路径及访问git的账号和密码 3.3 执行start.sh脚本 四. 浏览器访问jenkins执行任务...
Linux-Centos7安装Docker
文章目录 一、前言二、Docker安装1、Docker及系统版本2、Docker的自动化安装3、Docker手动安装3.1、卸载Docker(可选)3.2、设置源仓库3.3、Docker安装3.4、Docker启动3.5、验证是否安装成功3.5.1、拉取镜像3.5.2、查看镜像3.5.3、运行镜像 3.6、删除Dock…...

前端Vue入门-day06-路由进阶
(创作不易,感谢有你,你的支持,就是我前行的最大动力,如果看完对你有帮助,请留下您的足迹) 目录 路由的封装抽离 声明式导航 导航链接 两个类名 自定义高亮类名 跳转传参 1. 查询参数传参 2. 动态…...

数据库服务器是什么意思?数据库服务器有哪些?
数据库服务器是什么意思?现在市场上有很多的服务器的类型,比如数据库服务器,但是很多人对数据库服务器是什么意思?数据库服务器有哪些并不是很熟悉,那么,聚名企服为您详解一下。 一:数据库服务器是什么意思 数据库服…...

配电网智能软开关(sop)规划模型matlab
目录 1 主要内容 2 部分程序 3 程序结果 1 主要内容 该程序参考文献《基于改进灵敏度分析的有源配电网智能软开关优化配置》,采用二阶锥算法,以改进的IEEE33节点配电系统模型作为分析对象,以联络开关位置作为sop安装备选位置,以…...

Qt 常用函数
设置编码 #if (QT_VERSION < QT_VERSION_CHECK(5,0,0)) #if _MSC_VERQTextCodec *codec QTextCodec::codecForName("gbk"); #elseQTextCodec *codec QTextCodec::codecForName("utf-8"); #endifQTextCodec::setCodecForLocale(codec);QTextCodec::se…...

UMA 2 - Unity Multipurpose Avatar☀️六.Advanced Occlusion高级遮挡功能解决皮肤服饰穿模
文章目录 🟥 本节功能效果展示🟧 基础项目配置🟨 本节项目配置🟩 配置MeshHideAsset1️⃣ 创建MeshHideAsset2️⃣ 配置SlotDataAsset3️⃣ 配置遮挡信息🟦 将 MeshHideAsset 配置到 Recipe🟥 本节功能效果展示 未遮挡前的穿模问题: 遮挡后效果:...
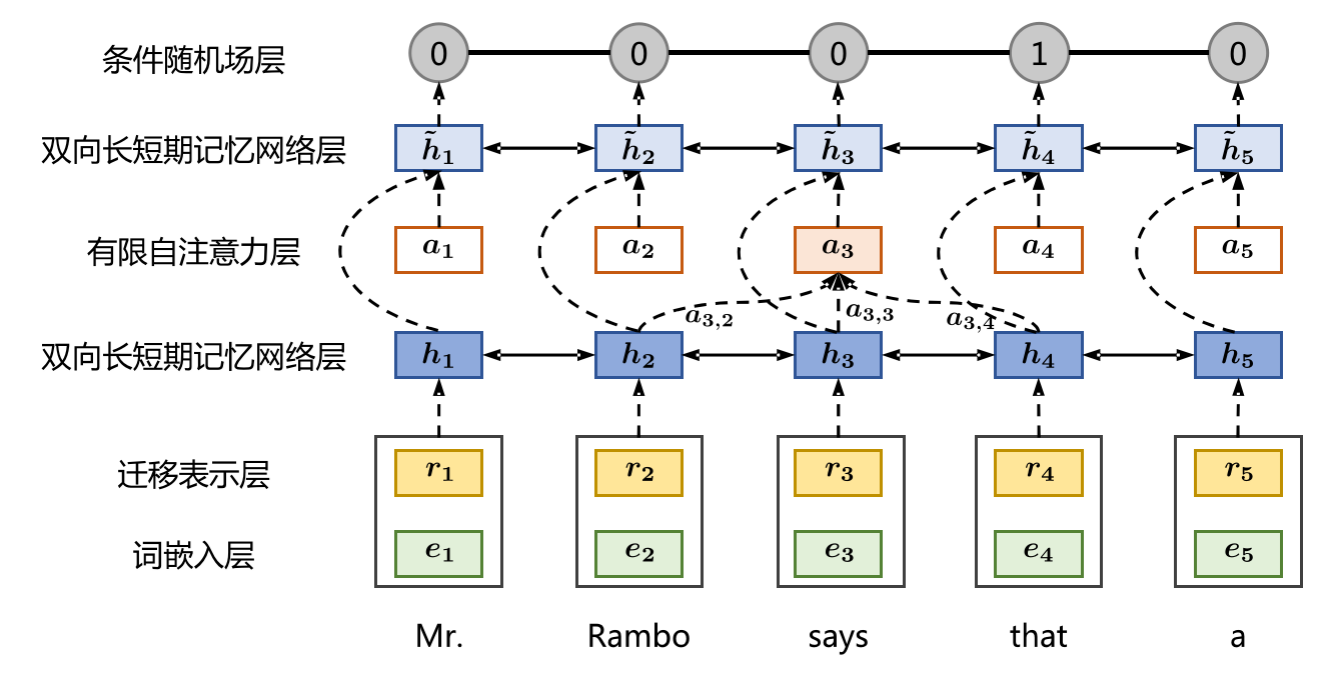
深度解析自然语言处理之篇章分析
在本文中,我们深入探讨了篇章分析的概念及其在自然语言处理(NLP)领域中的研究主题,以及两种先进的话语分割方法:基于词汇句法树的统计模型和基于BiLSTM-CRF的神经网络模型。 关注TechLead,分享AI全维度知识…...
、文件系统(os/ shutil/json/pickle/openpyxl/xlrd))
Python3.11教程3:模块和包(pip/conda)、文件系统(os/ shutil/json/pickle/openpyxl/xlrd)
文章目录 七、模块和包7.1 模块7.1.1 模块搜索路径7.1.2 PYTHONPATH和sys.path7.1.2 模块的导入和常见错误7.1.3 模块的缓存机制7.1.4 __name__ 和 __main__ 函数 7.2 标准库7.3 包7.3.1 创建包7.3.2 导入包7.3.3 pip包管理器7.3.4 conda 7.4 如何组织和管理大型项目中的模块与…...
)
shell 脚本工具(三剑客)
第一个:awk awk 是一种强大的文本处理工具和编程语言,最初由 Alfred Aho、Peter Weinberger 和 Brian Kernighan 在20世纪70年代早期创建。awk 的名称来自于这三位创造者的姓氏的首字母。它在 Unix 和类 Unix 操作系统中广泛使用,用于处理、…...
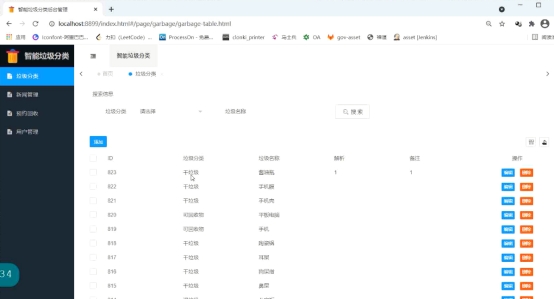
基于微信小程序的智能垃圾分类回收系统,附源码、教程
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝30W、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 1 简介 视频演示地址: 基于微信小程序的智能垃圾分类回收系统,可作为毕业设计 小…...

【C++进阶】:AVL树(平衡因子)
AVL树 一.概念二.插入1.搜索二叉树2.平衡因子 三.旋转1.更新平衡因子2.旋转1.左单旋2.右单旋3.先右旋再左旋4.先左旋再右旋 四.完整代码 一.概念 二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元…...
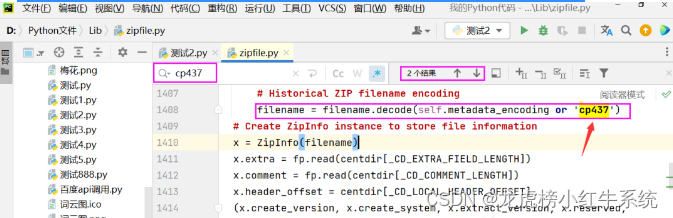
Python教程33:关于在使用zipfile模块,出现中文乱码的解决办法
zipfile是Python标准库中的一个模块,zipfile里有两个class, 分别是ZipFile和ZipInfo,用来创建和读取zip文件,而ZipInfo是存储的zip文件的每个文件的信息的。ZIP文件是一种常见的存档文件格式,它可以将多个文件和目录压缩为一个文件…...
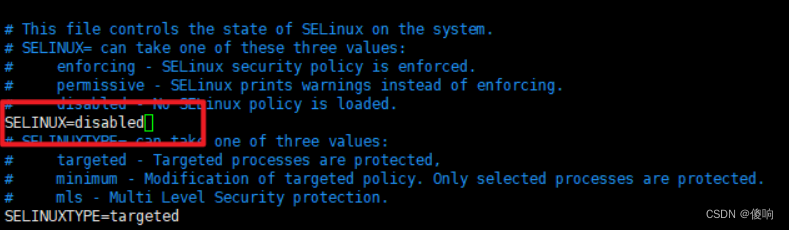
【疑难杂症】使用xshell连接云服务器连接不上
目录 【1】使用xshell连接云服务器连接不上 【1.1】解决方法一 【1.2】解决方法二 【1】使用xshell连接云服务器连接不上 Centos7使用xshell连接提示"ssh服务器拒绝了密码 请再试一次"。 问题如图所示,新安装了一台Centos7服务器,使用ssh连…...

Qt MinGW / MSVC
MinGW/MSVC的关系 MinGW / MSVC.dll / .lib / .a 的关系 MinGW / MSVC Qt 中有两种方式编译:一种是MinGW ,另一种MSVC,是两种不同的编译器。 MinGW(Minimalist GNUfor Windows),它是一个可自由使用和自由发布的Windows特定头文件…...

【数学建模】数据预处理
为什么需要数据预处理 数学建模是将实际问题转化为数学模型来解决的过程,而数据预处理是数学建模中非常重要的一步。以下是为什么要进行数据预处理的几个原因: 数据质量:原始数据往往存在噪声、异常值、缺失值等问题,这些问题会对…...
VMware 安装 黑群晖7.1.1-42962 DS918+
本例的用的文件 1、ARPL 1.0beat 引导文件 vmdk格式: https://download.csdn.net/download/mshxuyi/88309308 2、DS918_42962.pat:https://download.csdn.net/download/mshxuyi/88309383 一、引导文件 1、创建一个虚拟机 2、下一步,选稍后…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...
