代码随想录算法训练营day45|70. 爬楼梯(进阶版)|322. 零钱兑换|279.完全平方数
70. 爬楼梯(进阶版)
一步一个台阶,两个台阶,三个台阶,…,直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢?
1阶,2阶,… m阶就是物品,楼顶就是背包。
每一阶可以重复使用,例如跳了1阶,还可以继续跳1阶。
问跳到楼顶有几种方法其实就是问装满背包有几种方法。 求的是排列
class Solution {public int climbStairs(int n) {int[] dp = new int[n + 1];int m = 2; //m表示最多可以爬m个台阶dp[0] = 1;for (int i = 1; i <= n; i++) { // 遍历背包for (int j = 1; j <= m; j++) { //遍历物品if (i >= j) //當前的背包容量 大於 物品重量的時候,我們才需要記錄當前的這個裝得方法(方法數+)dp[i] += dp[i - j];}}return dp[n];}
}322. 零钱兑换
力扣题目链接
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
你可以认为每种硬币的数量是无限的。
示例 1:
- 输入:coins = [1, 2, 5], amount = 11
- 输出:3
- 解释:11 = 5 + 5 + 1
示例 2:
- 输入:coins = [2], amount = 3
- 输出:-1
示例 3:
- 输入:coins = [1], amount = 0
- 输出:0
示例 4:
- 输入:coins = [1], amount = 1
- 输出:1
示例 5:
- 输入:coins = [1], amount = 2
- 输出:2
提示:
1.确定dp数组以及下标的含义
背包容量: 目标值
硬币:物品
问:装满这个背包,最少用多少件物品
dp[j]:凑足总额为j所需钱币的最少个数为dp[j]
2.确定递推公式
Math.min
dp[j]=Math.min(dp[j],dp[j-coins[i]]+1)
3.初始化
首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0;
其他下标对应的数值呢?
考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在Math.min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
所以下标非0的元素都是应该是最大值。
//初始化dp数组为最大值for (int j = 0; j < dp.length; j++) {dp[j] = Integer.MAX_VALUE;}
4.遍历顺序求
求最小的元素数量 ,不影响 都可以
5.打印dp数组
以输入:coins = [1, 2, 5], amount = 5为例
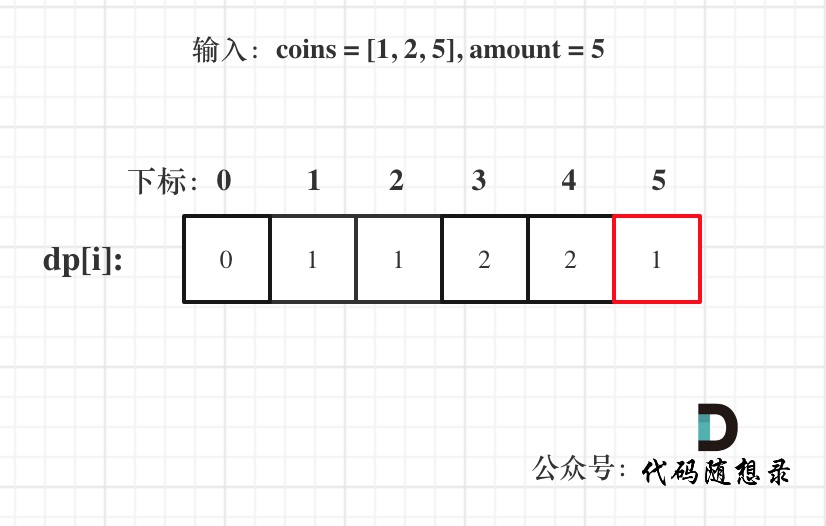
代码:
class Solution {public int coinChange(int[] coins, int amount) {int[] dp=new int[amount+1];//初始化 其他下标 因为要求最小所以不能赋值为0 会被覆盖for (int j = 0; j < dp.length; j++) {dp[j] = Integer.MAX_VALUE;}dp[0]=0;for(int i=0;i<coins.length;i++){ //遍历物品for(int j=coins[i];j<=amount;j++){ //遍历背包if(dp[j - coins[i]] != Integer.MAX_VALUE){// 如果dp[j - coins[i]]是初始值则跳过dp[j]=Math.min(dp[j],dp[j-coins[i]]+1);}}}return dp[amount]==Integer.MAX_VALUE?-1:dp[amount];}
}
279.完全平方数
力扣题目链接
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, …)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
给你一个整数 n ,返回和为 n 的完全平方数的 最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
- 输入:n = 12
- 输出:3
- 解释:12 = 4 + 4 + 4
示例 2:
- 输入:n = 13
- 输出:2
- 解释:13 = 4 + 9
提示:
1.确定dp数组的含义
背包容量: 整数n
物品:完全平方数 i*i
问题:给你一个整数 n ,返回和为 n 的完全平方数的 最少数量 。
dp[j]: 和为j时,完全平方数最少的数量为dp[j]
2.确定递推公式
dp[j]=Math.min(dp[j],dp[j-i*i]+1)
每个元素的数值用i*i表示
3.初始化
首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0;
其他下标对应的数值呢?
考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在Math.min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
所以下标非0的元素都是应该是最大值。
//初始化dp数组为最大值for (int j = 0; j < dp.length; j++) {dp[j] = Integer.MAX_VALUE;}
4.遍历顺序求
求最小的元素数量,不影响
5.打印dp数组
已输入n为5例,dp状态图如下:

dp[0] = 0 dp[1] = min(dp[0] + 1) = 1 dp[2] = min(dp[1] + 1) = 2 dp[3] = min(dp[2] + 1) = 3 dp[4] = min(dp[3] + 1, dp[0] + 1) = 1 dp[5] = min(dp[4] + 1, dp[1] + 1) = 2
最后的dp[n]为最终结果。
代码:
class Solution {public int numSquares(int n) {int[] dp=new int[n+1];for(int j=0;j<=n;j++){dp[j]=Integer.MAX_VALUE;}dp[0]=0;for(int i=1;i*i<=n;i++){ //遍历物品for(int j=i*i;j<=n;j++){ //遍历背包 背包从物品大小开始dp[j]=Math.min(dp[j],dp[j-i*i]+1); //为了下标不出现负数}}return dp[n];}
}
相关文章:

代码随想录算法训练营day45|70. 爬楼梯(进阶版)|322. 零钱兑换|279.完全平方数
70. 爬楼梯(进阶版) 一步一个台阶,两个台阶,三个台阶,…,直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢? 1阶,2阶,… m阶就是物品,楼顶就是背包。 每一阶可以重复使用&#…...

数据结构和算法(3):列表
列表是一种线性数据结构,它允许在其中存储多个元素,并且可以动态地添加或删除元素。 循秩访问 可通过重载下标操作符,实现寻秩访问 template <typename T> // assert: 0 < r < size T List<T>::operator[](Rank r) cons…...

使用playright自动下载vscode已安装插件
import os import re import subprocess import traceback from playwright.sync_api import Playwright, sync_playwright, expect# 执行CMD命令 cmd_command "code --list-extensions" # 获取已安装扩展列表 process subprocess.Popen(cmd_command, stdoutsubpr…...

单片机语言实例:2、点亮数码管的多种方法
一、共阳数码管静态显示 程序实例1: #include<reg52.h> //包含头文件,一般情况不需要改动, //头文件包含特殊功能寄存器的定义void main (void) {P10xc0; //二进制 为 1100 0000 参考数码管排列,//可以得出0对应的段点…...
C#学习 - 初识类与名称空间
类(class)& 名称空间(namespace) 类是最基础的 C# 类型,是一个数据结构,是构成程序的主体 名称空间以树型结构组织类 using System; //前面的using就是引用名称空间 //相当于C语言的 #include <..…...
Python爬取电影信息:Ajax介绍、爬取案例实战 + MongoDB存储
Ajax介绍 Ajax(Asynchronous JavaScript and XML)是一种用于在Web应用程序中实现异步通信的技术。它允许在不刷新整个网页的情况下,通过在后台与服务器进行数据交换,实时更新网页的一部分。Ajax的主要特点包括: 异步通…...

JavaScript的面向对象
一、认识对象 1.概述 对象(object)是 JavaScript 语言的核心概念,也是最重要的数据类型。 什么是对象?简单说,对象就是一组“键值对”(key-value)的集合,是一种无序的复合数据集合…...
MybatisPlus 核心功能 条件构造器 自定义SQL Service接口 静态工具
MybatisPlus 快速入门 常见注解 配置_软工菜鸡的博客-CSDN博客 2.核心功能 刚才的案例中都是以id为条件的简单CRUD,一些复杂条件的SQL语句就要用到一些更高级的功能了。 2.1.条件构造器 除了新增以外,修改、删除、查询的SQL语句都需要指定where条件。因此…...
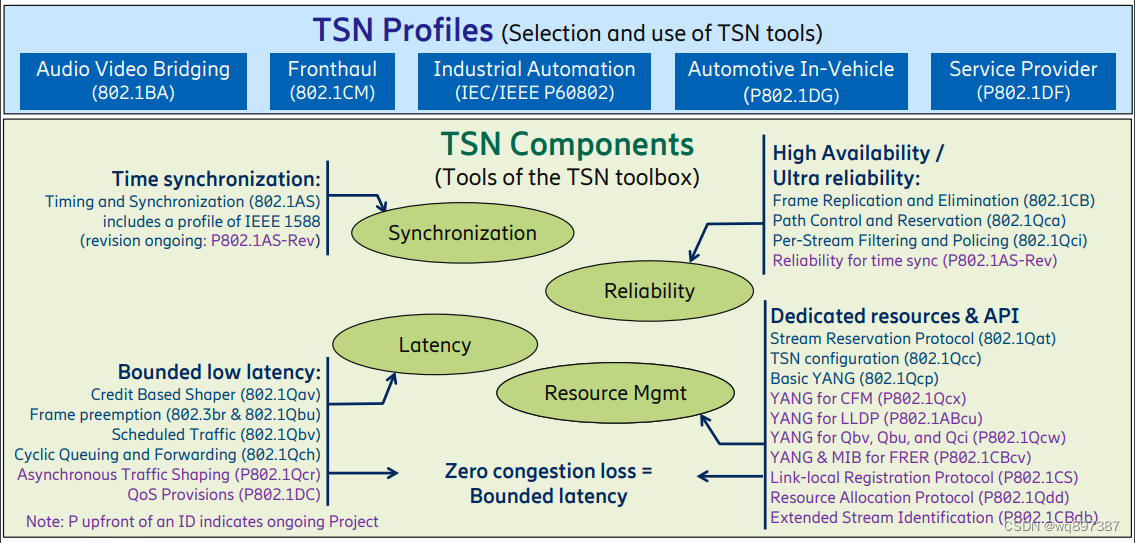
TSN时间敏感网络
目录 时间敏感网络介绍 子协议介绍 时间同步 IEEE802.1AS 调度和流量整形 IEEE802.1Q IEEE802.1Qbv IEEE802.1cr IEEE802.1Qbu IEEE802.1Qch IEEE802.1Qav IEEE802.1Qcc 纠错机制与安全 IEEE802.1Qci IEEE802.1CB IEEE802.1Qca 参考 时间敏感网络介绍 TSN(Tim…...

【2023年数学建模国赛】C题解题思路
第一问 要求分析分析蔬菜各品类及单品销售量的分布规律及相互关系。该问题可以拆分成三个角度进行剖析。 1)各种类蔬菜的销售量分布、蔬菜种类与销售量之间的关系;2)各种类蔬菜的销售量的月份分布、各种类蔬菜销售量与月份之间的相关关系&a…...

5分钟 将“.py”文件转为“.pyd”文件
代码: from distutils.core import setup from distutils.extension import Extension from Cython.Build import cythonize import osfile_list os.listdir("./") extensions [] for file in file_list:if file.endswith(".py") and file !…...
)
python 入门到精通(一)
文章目录 1.使用pycharm进行第一个程序的编写2.python基础语法篇2.1 常用的值类型2.2 注释2.3 变量2.4 数据类型2.5 数据类型转换2.6 什么是标识符2.7 运算符2.8 字符串扩展2.8.1 字符串拼接2.8.2 字符串格式化2.8.3 格式化的精度控制2.8.4 字符串格式化 - 快速写法2.8.5 字符串…...
异步的JavaScript 和 XML)
AJAX (Asynchronous JavaScript And XML)异步的JavaScript 和 XML
1、概念 Asynchronous JavaScript And XML 异步的JavaScript 和 XML异步和同步:客户端和服务器端相互通信的基础上 同步:客户端必须等待服务端的响应。在等待的期间客户端不能做其他操作。异步:客户端不需要等待服务器端的响应。在服务器…...
华为云云耀云服务器L实例评测|安装Java8环境 配置环境变量 spring项目部署 【!】存在问题未解决
目录 引出安装JDK8环境查看是否有默认jar上传Linux版本的jar包解压压缩包配置环境变量 上传jar包以及运行问题上传Jar包运行控制台开放端口访问失败—见问题记录关闭Jar的方式1.进程kill -92.ctrl c退出 问题记录:【!】未解决各种方式查看端口情况联系工程师最后排查…...
安卓多渠道打包(五)360加固walle多渠道打包
背景: 1、360加固宝,签名收費了,脚本上传加固也针对特定帐号才可实现。 内容 本文将会分享安卓项目中,使用360加固,再用walle签名,产出多渠道加固包的全流程。 环境 win10 jdk11 as2022 gradle7.5 最…...

Jmeter 实现 mqtt 协议压力测试
1. 下载jmeter,解压 https://jmeter.apache.org/download_jmeter.cgi 以 5.4.3 为例,下载地址: https://dlcdn.apache.org//jmeter/binaries/apache-jmeter-5.4.3.zip linux下解压: unzip apache-jmeter-5.4.3.zip 2. 下载m…...
蓝桥杯官网练习题(凑算式)
类似填空题: ①算式900: https://blog.csdn.net/s44Sc21/article/details/132746513?spm1001.2014.3001.5501https://blog.csdn.net/s44Sc21/article/details/132746513?spm1001.2014.3001.5501 ②九宫幻方③七星填数④幻方填空:https:/…...
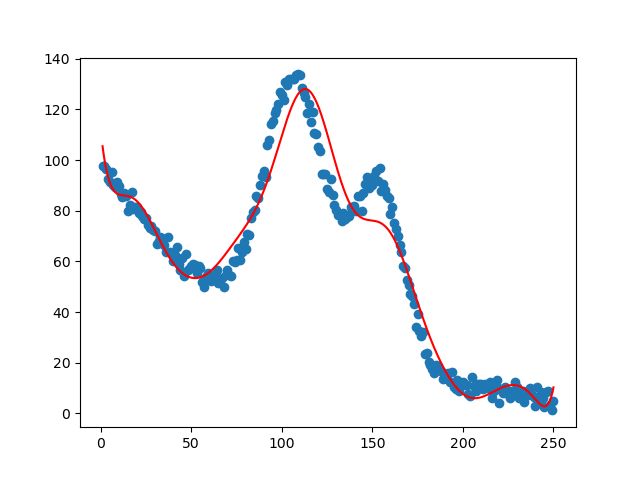
机器学习实战-系列教程5:手撕线性回归4之非线性回归(项目实战、原理解读、源码解读)
🌈🌈🌈机器学习 实战系列 总目录 本篇文章的代码运行界面均在Pycharm中进行 本篇文章配套的代码资源已经上传 手撕线性回归1之线性回归类的实现 手撕线性回归2之单特征线性回归 手撕线性回归3之多特征线性回归 手撕线性回归4之非线性回归 1…...

【C语言基础】那些你可能不知道的C语言“潜规则”
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…...
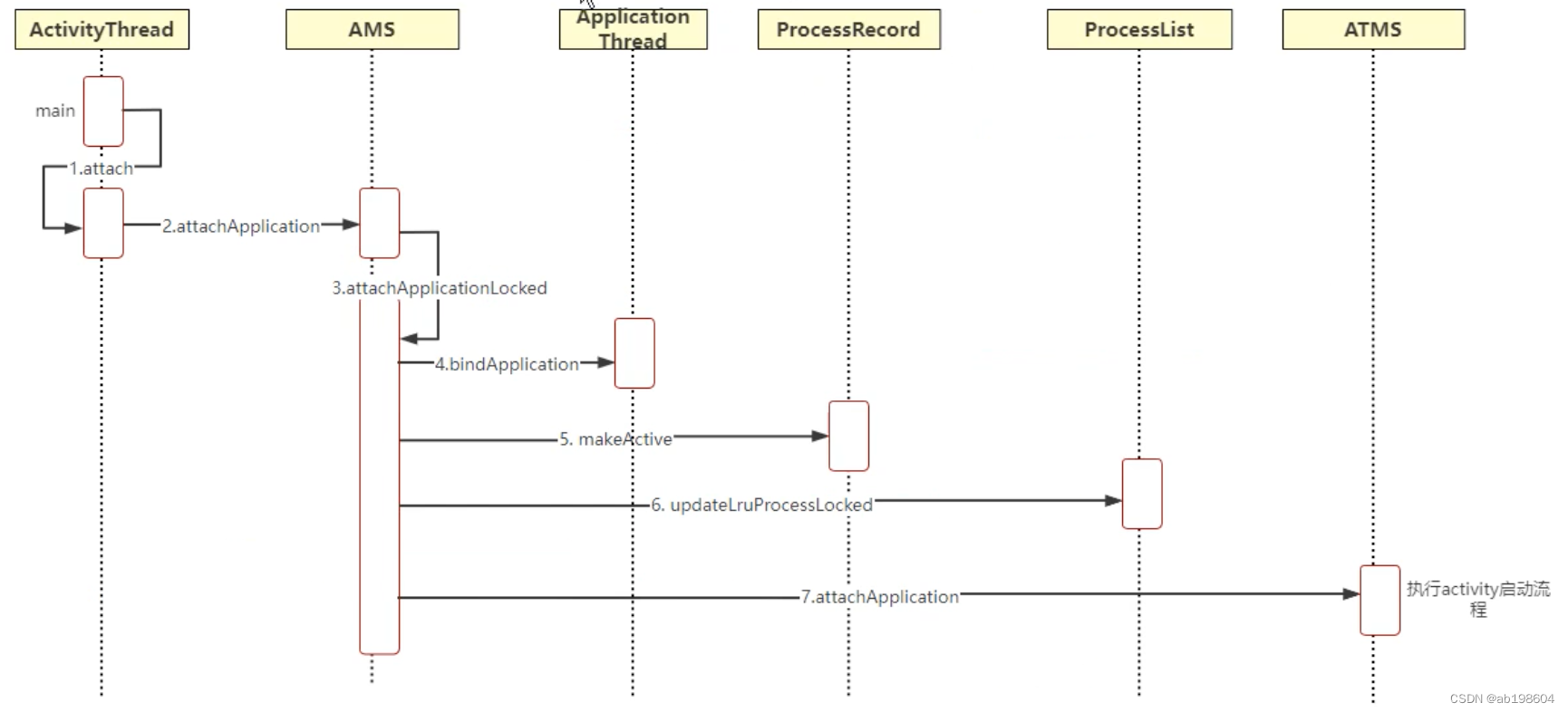
android framework之Applicataion启动流程分析(三)
现在再回顾一下Application的启动流程,总的来说,虽然进程的发起是由ATMS服务发起的,但是进程的启动还是由AMS负责,所以需要调用AMS的startProcess()接口完成进程启动流程,AMS要处理的事情很多,它将事务交给…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...
