【C++模拟实现】手撕AVL树
【C++模拟实现】手撕AVL树
目录
- 【C++模拟实现】手撕AVL树
- AVL树的介绍(百度百科)
- AVL树insert函数的实现代码
- 验证是否为AVL树
- AVL树模拟实现的要点
- 易忘点
- AVL树的旋转思路
作者:爱写代码的刚子
时间:2023.9.10
前言:本篇博客将会介绍AVL树的模拟实现(模拟AVL树的插入),以及如何去验证是否为AVL树
AVL树的介绍(百度百科)
AVL树本质上还是一棵二叉搜索树,它的特点是:
-
本身首先是一棵二叉搜索树。
-
带有平衡条件:每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1。
也就是说,AVL树,本质上是带了平衡功能的二叉查找树(二叉排序树,二叉搜索树)。
AVL树insert函数的实现代码
template<class K,class V>
class AVLTreeNode
{
public:AVLTreeNode(const pair<K,V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_bf(0){}AVLTreeNode* _left;AVLTreeNode* _right;AVLTreeNode* _parent;//需要设立父节点指针pair<K,V> _kv;int _bf;
};template<class K,class V>
class AVLTree
{typedef AVLTreeNode<K,V> Node;
public:AVLTree():_root(nullptr){}bool insert(const pair<K,V>& kv){if(_root==nullptr){_root=new Node(kv);return true;}else{Node* cur=_root;Node* parent=nullptr;//设计parent指针是必要的while(cur){if(cur->_kv.first>kv.first){parent=cur;cur=cur->_left;}else if(cur->_kv.first<kv.first){parent=cur;cur=cur->_right;}else{return false;}}cur=new Node(kv);//判断新加入的节点是父节点的左子树还是右子树if(parent->_kv.first>kv.first){parent->_left=cur;}else{parent->_right=cur;}cur->_parent=parent;while(parent){//及时调整父节点的平衡因子if(parent->_left==cur){--parent->_bf;}else{++parent->_bf;}if(parent->_bf==0)//当父节点的平衡因子为0时停止调整{break;}else if(parent->_bf==-1||parent->_bf==1){cur=parent;parent=parent->_parent;}else if(parent->_bf==2||parent->_bf==-2)//处理异常情况{//出现问题的情况if(parent->_bf==-2&&cur->_bf==-1){_RotateR(parent);//右单旋}else if(parent->_bf==2&&cur->_bf==1){_RotateL(parent);//左单旋}else if(parent->_bf==-2&&cur->_bf==1){ _RotateLR(parent);//左右双旋}else if(parent->_bf==2&&cur->_bf==-1){_RotateRL(parent);//右左双旋}else{assert(false);}break;}else{assert(false);}}}return true;} void _RotateR(Node* parent)//右单旋的实现{Node*cur=parent->_left;Node*curRight=cur->_right;Node*ppnode=parent->_parent;cur->_right=parent;parent->_left=curRight;if(curRight)//curRight可能是nullptr{curRight->_parent=parent;}parent->_parent=cur;//处理ppnodeif(parent==_root)//parent为头节点时需要单独处理{_root=cur;cur->_parent=nullptr;}else{if(ppnode->_left==parent){ppnode->_left=cur;}else{ppnode->_right=cur;}cur->_parent=ppnode;}parent->_bf=cur->_bf=0;}void _RotateL(Node* parent){Node* cur=parent->_right;Node* curLeft=cur->_left;Node* ppnode=parent->_parent;cur->_left=parent;parent->_right=curLeft;if(curLeft){curLeft->_parent=cur;}parent->_parent=cur;if(parent==_root){_root=cur;cur->_parent=nullptr;}else{if(ppnode->_left==parent){ppnode->_left=cur;}else{ppnode->_right=cur;}cur->_parent=ppnode;}parent->_bf=cur->_bf=0;}void _RotateLR(Node* parent){Node* cur=parent->_left;Node* curRight=cur->_right;int bf=curRight->_bf;_RotateL(cur);_RotateR(parent);//最好再处理一下平衡因子,减少耦合度if(bf==0)//单链情况下{parent->_bf=0;cur->_bf=0;curRight->_bf=0;}else if(bf==-1){parent->_bf=1;curRight->_bf=0;cur->_bf=0;}else if(bf==1){parent->_bf=-1;curRight->_bf=0;cur->_bf=0;}else{assert(false);}}void _RotateRL(Node* parent){Node* cur=parent->_right;Node* curLeft=cur->_left;int bf=curLeft->_bf;_RotateR(cur);_RotateL(parent);if(bf==0){parent->_bf=0;curLeft->_bf=0;cur->_bf=0;}else if(bf==1){parent->_bf=0;curLeft->_bf=-1;cur->_bf=0;}else if(bf==-1){parent->_bf=0;curLeft->_bf=1;cur->_bf=0;}else{assert(false);}}private:Node* _root;
};验证是否为AVL树
int _Height(Node* root){if(root==nullptr){return 0;}int leftHeight=_Height(root->_left);int rightHeight=_Height(root->_right);return leftHeight>rightHeight?leftHeight+1:rightHeight+1;}bool _Isbalance(){return _Isbalance(_root);}bool _Isbalance(Node* root){if(root==nullptr){return true;}int right=_Height(root->_right);int left=_Height(root->_left);if(root->_bf!=right-left){cout<<"平衡因子异常"<<root->_bf<<" "<<right<<" "<<left<<endl;return false;}return abs(right-left)<2&&_Isbalance(root->_left)&&_Isbalance(root->_right);}
-
根据AVL树的特性引入两个成员函数_Height函数用于计算二叉树的高度
-
以下为验证结果:

AVL树模拟实现的要点
易忘点
一定要时刻注意_parent指针的修改!尤其旋转函数中需要判断旋转后的二叉树的根节点是否还有父亲节点,如果有,需要在旋转前先保存,之后再链接上。
AVL树的旋转思路
- 新增在左,parent平衡因子减减
- 新增在右,parent平衡因子加加
- 更新后parent平衡因子 == 0,说明parent所在的子树的高度不变,不会再影响祖先,不用再继续沿着到eot的路径往上更新
- 更新后parent平衡因子 == 1 0r -1,说明parent所在的子树的高度变化,会再影响祖先,需要继续沿着到root的路径往上更新更新后
- 更新后parent平衡因子 == 2 or -2,说明parent所在的子树的高度变化且不平衡,对parent所在子树进行旋转,让他平衡
- 更到根节点,插入结束
由于AVL树画图较为麻烦,作者先不画了,可以看看其他大佬的博客,一些需要注意的地方已经写在代码注释里了,AVL树的删除之后有机会可以模拟实现一下。
AVL树的调试较为麻烦,模拟实现可以提高自己的调试能力。
相关文章:

【C++模拟实现】手撕AVL树
【C模拟实现】手撕AVL树 目录 【C模拟实现】手撕AVL树AVL树的介绍(百度百科)AVL树insert函数的实现代码验证是否为AVL树AVL树模拟实现的要点易忘点AVL树的旋转思路 作者:爱写代码的刚子 时间:2023.9.10 前言:本篇博客将…...

如何重置 docker中的mariadb的root
停止 Mariadb 容器:运行以下命令停止正在运行的 Mariadb 容器: docker stop <container_name>将 <container_name> 替换为你的 Mariadb 容器的名称或容器ID。 删除 Mariadb 容器:运行以下命令删除已停止的 Mariadb 容器&#x…...

设计模式系列-原型模式
一、上篇回顾 上篇创建者模式中,我们主要讲述了创建者的几类实现方案,和创建者模式的应用的场景和特点,创建者模式适合创建复杂的对象,并且这些对象的每 个组成部分的详细创建步骤可以是动态的变化的,但是每个对象的组…...

家用电脑可以用做服务器吗
家用电脑的结构与服务器的结构是相同的,家用电脑是可以用来搭建服务器使用。但使用家用电脑做服务器在稳定性会比服务器差很多 1.家用电脑没有公网IP,网络运营商分配的IP重启路由之后是会变化,不固定。服务器运行是需要有固定IP让人连接访问。…...

CRM软件管理系统的基本功能
CRM管理系统是企业运营的重要工具,它可以帮助企业管理客户关系,提升销售效率,大幅提高客户转化率,实现业绩增长。那么,CRM管理系统一般包含哪些功能呢?下面我们就来说说。 1、销售自动化 销售自动化顾名思…...

手机喊话应用实现思路
手机要是动一下,就喊话“摇摇零线,摇摇零线”,是不是比较酷, 这里实现一下手机翻转一下,播放声音的效果, 通过sensor识别到手机的运动状况,然后播放音频, public class MainActivi…...

【ARM CoreLink 系列 3 -- CCI-550 控制器介绍 】
文章目录 CCI FamilyCCI-550 简介CCI-550 功能CCI-550 Interfaces Snoop filter 使用背景CCI-550 Snoop filter 上篇文章:ARM CoreLink 系列 2 – CCI-400 控制器简介 CCI Family CCI-550 简介 Arm CoreLink CCI-550 Cache Coherent Interconnect 扩展了 CoreLink…...

最长递增子序列 -- 动规
300. 最长递增子序列 注意「⼦序列」和「⼦串」的区别,⼦串⼀定是连续的,⽽⼦序列不⼀定是连续的。 class LengthOfLIS:"""300. 最长递增子序列https://leetcode.cn/problems/longest-increasing-subsequence/description/""&q…...

linux 进程管理命令
进程管理命令 查看进程命令 ps命令 显示系统上运行的进程列表 # 查看系统中所有正在运行的系统ps aux# 获取占用内存资源最多的10个进程,可以使用如下命令组合:ps aux|head -1;ps aux|grep -v PID|sort -rn -k 4|head# 获取占用CPU资源最多的10个进程&am…...

第一章:计算机网络和因特网
什么是因特网 具体构成描述 互联网是一个世界范围的计算机网络,即一个互联了遍及世界数十亿计算机设备的网络,这些被连接的设备被称为主机或者端系统。端系统通过通信链路(communication link)和分组交换机(packet s…...
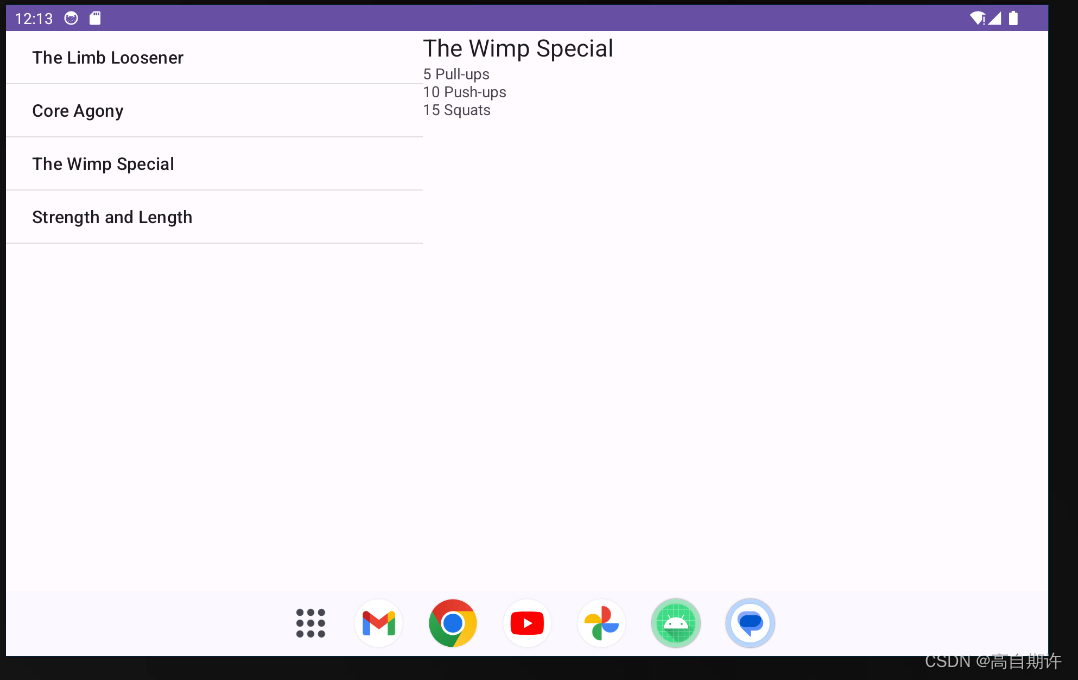
Android后退堆栈
修改代码 现在的ItemClick使得用户单击其中一个项目时就会跳转,现在要修改其使得在一个小屏幕设备上才会这样做,在一个大屏幕设备上运行用户选择一个训练项目时在右边的片段显示响应的信息。 希望片段处理后退的方式:假设用户在手机上运行这…...
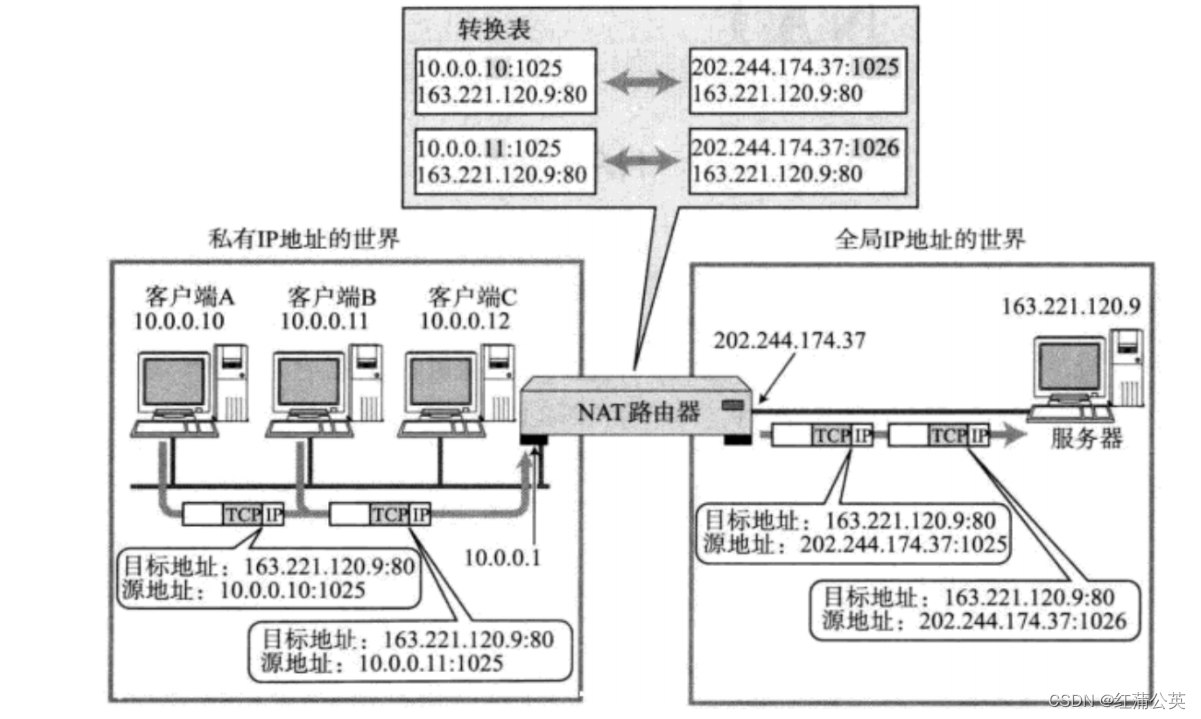
网络原理(一)网络基础,包括IP ,网络相关的定义
网络基础,包括IP ,网络相关的定义 网络基础冲突域广播域DNSNATNAPT 网络基础 以下图片是书上的网图。 什么是IP地址? IP地址(Internet Protocol Address)是指互联网协议地址,又译为网际协议地址。P地址是…...

Python语义分割与街景识别(2):环境搭建
前言 本文主要用于记录我在使用python做图像识别语义分割训练集的过程,由于在这一过程中踩坑排除BUG过多,因此也希望想做这部分内容的同学们可以少走些弯路。 本文是python语义分割与街景识别的第二篇,关于环境搭建的内容。这个部分是整个流…...
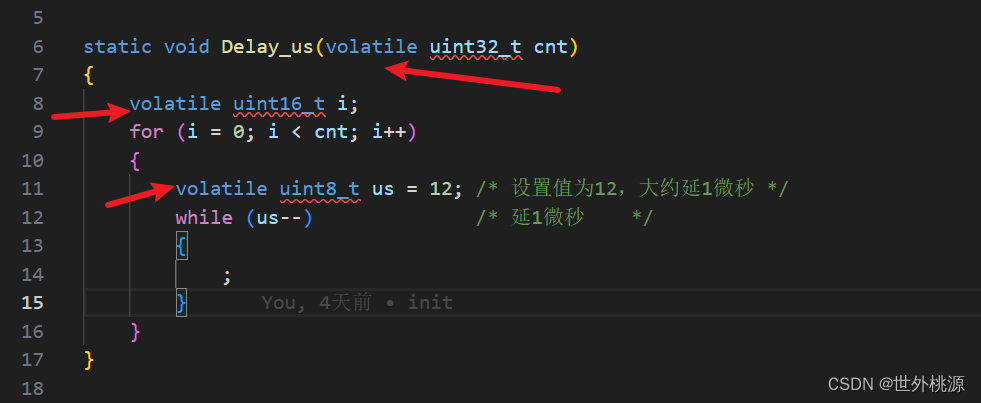
stm32(GD32,apm32),开优化后需要特别注意的地方
提到优化就不得不提及 volatile 使用场景 1:中断服务程序中修改的供其它程序检测的变量,需要加volatile; : 2:多任务环境下各任务间共享的标志,应该加volatile; 3:并行设备的硬件寄存器&#x…...

LLVM 与代码混淆技术
项目源码 什么是 LLVM LLVM 计划启动于2000年,开始由美国 UIUC 大学的 Chris Lattner 博士主持开展,后来 Apple 也加入其中。最初的目的是开发一套提供中间代码和编译基础设施的虚拟系统。 LLVM 命名最早源自于底层虚拟机(Low Level Virtu…...

R语言---使用runway进行机器学习模型性能的比较
R语言—使用runway进行机器学习模型性能的比较 #dataloadrm(list=ls())#librarylibrary(dcurves)library(gtsummary)library(tidyverse)library(mlr3verse)library(tidyverse)library(data.table)</...
C++斩题录|递归专题 | leetcode50. Pow(x, n)
个人主页:平行线也会相交 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创 收录于专栏【手撕算法系列专栏】【LeetCode】 🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望…...

详解Redis之Lettuce实战
摘要 是 Redis 的一款高级 Java 客户端,已成为 SpringBoot 2.0 版本默认的 redis 客户端。Lettuce 后起之秀,不仅功能丰富,提供了很多新的功能特性,比如异步操作、响应式编程等,还解决了 Jedis 中线程不安全的问题。 …...

【3】单着色器文件读取
Basic.shader文件,可以发现顶点着色器和片段着色器是写在一个文件里的,这里我们将他们读取出来,而不是上一篇使用string的方式。 #shader vertex #version 330 corelayout(location 0) in vec4 position;void main() {gl_Position positio…...

祝贺埃文科技入选河南省工业企业数据安全技术支撑单位
近日,河南省工业信息安全产业发展联盟公布了河南省工业信息安全应急服务支撑单位和河南省工业企业数据安全技术支撑单位遴选结果,最终评选出19家单位作为第一届河南省工业信息安全应急服务支撑单位和河南省工业企业数据安全技术支撑单位。 埃文科技凭借自身技术优势…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...
