【LeetCode算法系列题解】第61~65题
CONTENTS
- LeetCode 61. 旋转链表(中等)
- LeetCode 62. 不同路径(中等)
- LeetCode 63. 不同路径 II(中等)
- LeetCode 64. 最小路径和(中等)
- LeetCode 65. 有效数字(困难)
LeetCode 61. 旋转链表(中等)
【题目描述】
给你一个链表的头节点 head,旋转链表,将链表每个节点向右移动 k 个位置。
【示例1】
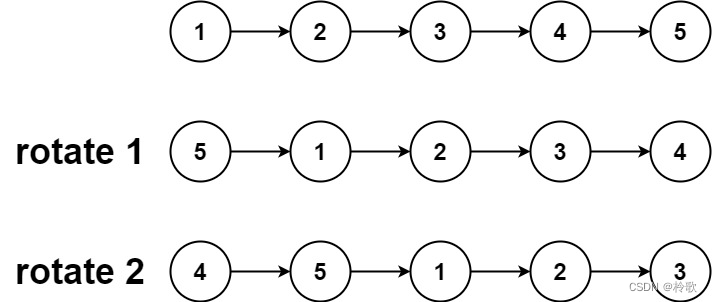
输入:head = [1,2,3,4,5], k = 2
输出:[4,5,1,2,3]
【示例2】
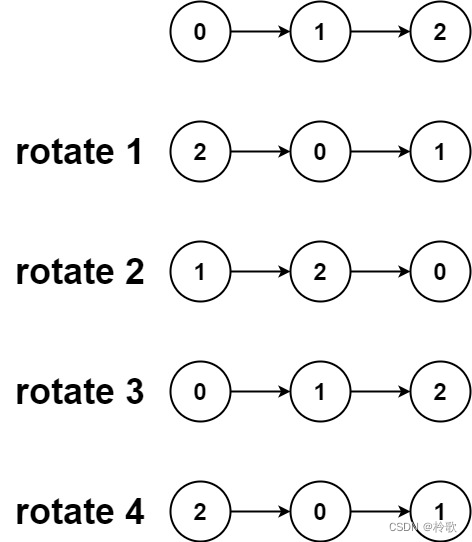
输入:head = [0,1,2], k = 4
输出:[2,0,1]
【提示】
链表中节点的数目在范围 [0, 500] 内
− 100 ≤ N o d e . v a l ≤ 100 -100\le Node.val\le 100 −100≤Node.val≤100
0 ≤ k ≤ 2 ∗ 1 0 9 0\le k\le 2 * 10^9 0≤k≤2∗109
【分析】
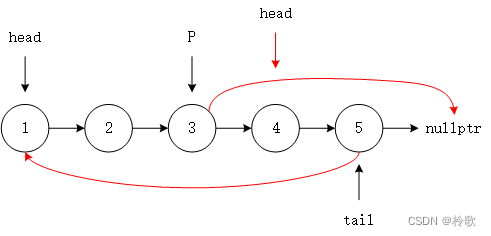
首先由于 k k k 可能很大,当 k k k 超过链表结点数 n n n 时,就变成了重复的循环位移,因此 k k k 需要先对 n n n 取模。
以样例1为例,示意图如上图所示,算法流程如下:
- 先遍历一遍链表,求出链表长度 n n n,并记下最后一个结点
tail; - 我们需要将链表的最后 k k k 个结点移动到首部,因此需要先找到倒数第 k + 1 k+1 k+1 个结点
P,也就是正数第 n − k n-k n−k 个结点,那么就需要从头结点向后遍历 n − k − 1 n-k-1 n−k−1 次; tail->next = headhead = P->nextP->next = nullptr
【代码】
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* rotateRight(ListNode* head, int k) {if (!head) return head; // 需要特判链表为空的情况ListNode* tail;int n = 0;for (auto p = head; p; p = p->next) n++, tail = p;k %= n;auto p = head;for (int i = 0; i < n - k - 1; i++) p = p->next;tail->next = head, head = p->next, p->next = nullptr;return head;}
};
LeetCode 62. 不同路径(中等)
【题目描述】
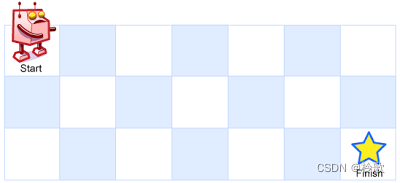
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start”)。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
问总共有多少条不同的路径?
【示例1】
输入:m = 3, n = 7
输出:28
【示例2】
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
【示例3】
输入:m = 7, n = 3
输出:28
【示例4】
输入:m = 3, n = 3
输出:6
【提示】
1 ≤ m , n ≤ 100 1\le m, n\le 100 1≤m,n≤100
题目数据保证答案小于等于 2 ∗ 1 0 9 2 * 10^9 2∗109
【分析】
本题是动态规划的数字三角形模型中的裸题,我们定义 f[i][j] 表示从起点走到点 (i, j) 的路径方案数,那么状态的转移有以下几种情况:
- 如果在第一行,那么只能从左边的点转移过来,即
f[i][j] = f[i][j - 1]; - 如果在第一列,那么只能从上边的点转移过来,即
f[i][j] = f[i - 1][j]; - 否则既能从左边转移过来也可以从上边转移过来,即
f[i][j] = f[i][j - 1] + f[i - 1][j]。
【代码】
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> f(m, vector<int>(n));f[0][0] = 1;for (int i = 0; i < m; i++)for (int j = 0; j < n; j++){if (i) f[i][j] += f[i - 1][j];if (j) f[i][j] += f[i][j - 1];}return f[m - 1][n - 1];}
};
LeetCode 63. 不同路径 II(中等)
【题目描述】
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start”)。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。

【示例1】
输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
【示例2】
输入:obstacleGrid = [[0,1],[0,0]]
输出:1
【提示】
m = = o b s t a c l e G r i d . l e n g t h m == obstacleGrid.length m==obstacleGrid.length
n = = o b s t a c l e G r i d [ i ] . l e n g t h n == obstacleGrid[i].length n==obstacleGrid[i].length
1 ≤ m , n ≤ 100 1\le m, n\le 100 1≤m,n≤100
obstacleGrid[i][j] 为 0 或 1
【分析】
和上一题一样,如果 (i, j) 是障碍物,则 f[i][j] = 0,即没有办法走到这个点。如果起点或者终点是障碍物,那么直接返回 0 0 0 即可。
【代码】
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int n = obstacleGrid.size(), m = obstacleGrid[0].size();if (obstacleGrid[0][0] || obstacleGrid[n - 1][m - 1]) return 0; // 特判起点或终点就是障碍物的情况vector<vector<int>> f(n, vector<int>(m));f[0][0] = 1;for (int i = 0; i < n; i++)for (int j = 0; j < m; j++)if (!obstacleGrid[i][j]) // 如果是障碍物f[i][j]就为0,直接跳过不计算{if (i) f[i][j] += f[i - 1][j];if (j) f[i][j] += f[i][j - 1];}return f[n - 1][m - 1];}
};
LeetCode 64. 最小路径和(中等)
【题目描述】
给定一个包含非负整数的 m x n 网格 grid,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
【示例1】
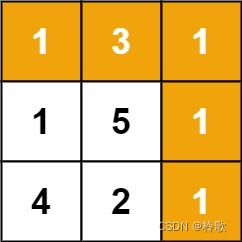
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
【示例2】
输入:grid = [[1,2,3],[4,5,6]]
输出:12
【提示】
m = = g r i d . l e n g t h m == grid.length m==grid.length
n = = g r i d [ i ] . l e n g t h n == grid[i].length n==grid[i].length
1 ≤ m , n ≤ 200 1\le m, n\le 200 1≤m,n≤200
0 ≤ g r i d [ i ] [ j ] ≤ 200 0\le grid[i][j]\le 200 0≤grid[i][j]≤200
【分析】
这题同样也是数字三角形模型,令 f[i][j] 表示从起点走到 (i, j) 的路径和的最小值,状态转移有如下几种情况:
- 从上边转移过来,那么结果为从起点走到
(i - 1, j)的路径和的最小值(f[i - 1][j])加上当前点的值,即f[i][j] = f[i - 1][j] + grid[i][j]; - 从左边转移过来同理,转移方程为:
f[i][j] = f[i][j - 1] + grid[i][j]。
根据 f[i][j] 的定义,我们要求的是最小值,因此最终的状态转移方程为:f[i][j] = min(f[i - 1][j], f[i][j - 1]) + grid[i][j]。
【代码】
class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int n = grid.size(), m = grid[0].size();vector<vector<int>> f(n, vector<int>(m, INT_MAX)); // 初始化为正无穷之后便于和自身取minf[0][0] = grid[0][0];for (int i = 0; i < n; i++)for (int j = 0; j < m; j++){if (i) f[i][j] = min(f[i][j], f[i - 1][j] + grid[i][j]);if (j) f[i][j] = min(f[i][j], f[i][j - 1] + grid[i][j]);}return f[n - 1][m - 1];}
};
LeetCode 65. 有效数字(困难)
【题目描述】
有效数字(按顺序)可以分成以下几个部分:
- 一个小数或者整数
- (可选)一个
'e'或'E',后面跟着一个整数
小数(按顺序)可以分成以下几个部分:
- (可选)一个符号字符(
'+'或'-') - 下述格式之一:
- 至少一位数字,后面跟着一个点
'.' - 至少一位数字,后面跟着一个点
'.',后面再跟着至少一位数字 - 一个点
'.',后面跟着至少一位数字
- 至少一位数字,后面跟着一个点
整数(按顺序)可以分成以下几个部分:
- (可选)一个符号字符(
'+'或'-') - 至少一位数字
部分有效数字列举如下:["2", "0089", "-0.1", "+3.14", "4.", "-.9", "2e10", "-90E3", "3e+7", "+6e-1", "53.5e93", "-123.456e789"]
部分无效数字列举如下:["abc", "1a", "1e", "e3", "99e2.5", "--6", "-+3", "95a54e53"]
给你一个字符串 s,如果 s 是一个有效数字,请返回 true。
【示例1】
输入:s = "0"
输出:true
【示例2】
输入:s = "e"
输出:false
【示例3】
输入:s = "."
输出:false
【提示】
1 ≤ s . l e n g t h ≤ 20 1\le s.length\le 20 1≤s.length≤20
s 仅含英文字母(大写和小写),数字(0-9),加号 '+',减号 '-',或者点 '.'。
【分析】
本题需要考虑的情况有很多种,我们一个个分析:
e/E的前后如果为空(在第一个或最后一个位置上),返回false;xx.或者.xx都是合法的,但是.e/E是不合法的;e/E的后面如果有.,返回false;+/-只可能在首部或者e/E的后面出现一次,其余地方出现均不合法;- 如果
.或者e/E出现次数大于1次则不合法; e/E的后面如果是+/-,还需要判断下一位有没有内容,如果已经到字符串末尾,也是不合法;- 其余情况只要不是
0~9即为不合法。
【代码】
class Solution {
public:bool isNumber(string s) {bool has_dot = false, has_e = false;if (s[0] == '+' || s[0] == '-') s = s.substr(1);if (s.empty()) return false; // 字符串只有+/-if (s[0] == '.' && (s.size() == 1 || s[1] == 'e' || s[1] == 'E')) return false;for (int i = 0; i < s.size(); i++){if (s[i] == '.'){if (has_dot || has_e) return false;has_dot = true;}else if (s[i] == 'e' || s[i] == 'E'){if (has_e || !i || i == s.size() - 1) return false; // 不止一次出现E或者出现在第一个或最后一个位置if (s[i + 1] == '+' || s[i + 1] == '-') // E后面是正负号还需要继续判断{if (i + 1 == s.size() - 1) return false;i++; // 跳过正负号}has_e = true;}else if (s[i] < '0' || s[i] > '9') return false;}return true;}
};
相关文章:

【LeetCode算法系列题解】第61~65题
CONTENTS LeetCode 61. 旋转链表(中等)LeetCode 62. 不同路径(中等)LeetCode 63. 不同路径 II(中等)LeetCode 64. 最小路径和(中等)LeetCode 65. 有效数字(困难ÿ…...

MATLAB中fillmissing函数用法
目录 语法 说明 示例 包含 NaN 值的向量 由 NaN 值组成的矩阵 插入缺失数据 使用移动中位数方法 使用自定义填充方法 包含缺失端点的矩阵 包含多个数据类型的表 fillmissing函数的功能是填充缺失的条目。 语法 F fillmissing(A,constant,v) F fillmissing(A,meth…...

电脑同时连接有线和无线网络怎么设置网络的优先级
电脑同时连接有线和无线网络怎么设置网络的优先级: 我们知道在 笔记本电脑系统 中,可以通过有线或无线网络进行联网。如果电脑在有线网络和无线网络同时存在的情况,应该怎么设置有线网络优先连接呢?对此我们提供下面的方法可以让电脑在有Wi…...

el-form表单动态校验(场景: 输入框根据单选项来动态校验表单 没有选中的选项就不用校验)
el-form表单动态校验 el-form常规校验方式: // 结构部分 <el-form ref"form" :model"form" :rules"rules"><el-form-item label"活动名称: " prop"name" required><el-input v-model"form.name" /…...

Java 数据结构与算法应该如何学习?
学习数据结构是计算机科学和软件工程领域中的重要基础知识之一。掌握数据结构对于编写高效、可扩展和可维护的代码至关重要。 1、掌握基本概念 首先,你需要掌握数据结构的基本概念。了解不同类型的数据结构,如数组、链表、栈、队列、树、图等ÿ…...

力扣(LeetCode)算法_C++——有效的数独
请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。 数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图) …...

制造企业如何优化物料控制?
导 读 ( 文/ 2127 ) 物料控制是指对制造过程中所涉及的物料流动和库存进行有效管理和控制的过程。它包括物料需求计划、供应商管理、物料采购、物料接收和入库、物料库存管理以及物料发放和使用等关键环节。通过精确的物料需求计划和库存管理,物料控制可以确保物料供…...

《Go语言在微服务中的崛起:为什么Go是下一个后端之星?》
🌷🍁 博主猫头虎🐅🐾 带您进入 Golang 语言的新世界✨✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文并茂…...
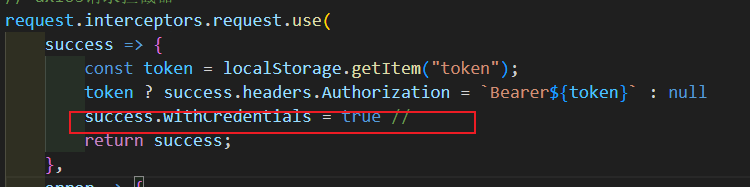
因为axios请求后端,接收不到token的问引出的问题
vue axios请求后端接受不到token的问题。 相关概念 什么是跨域? 跨域指的是在浏览器环境下,当发起请求的域(或者网站)与请求的资源所在的域之间存在协议、主机或端口中的任何一个条件不同的情况。换句话说,只要协议、…...
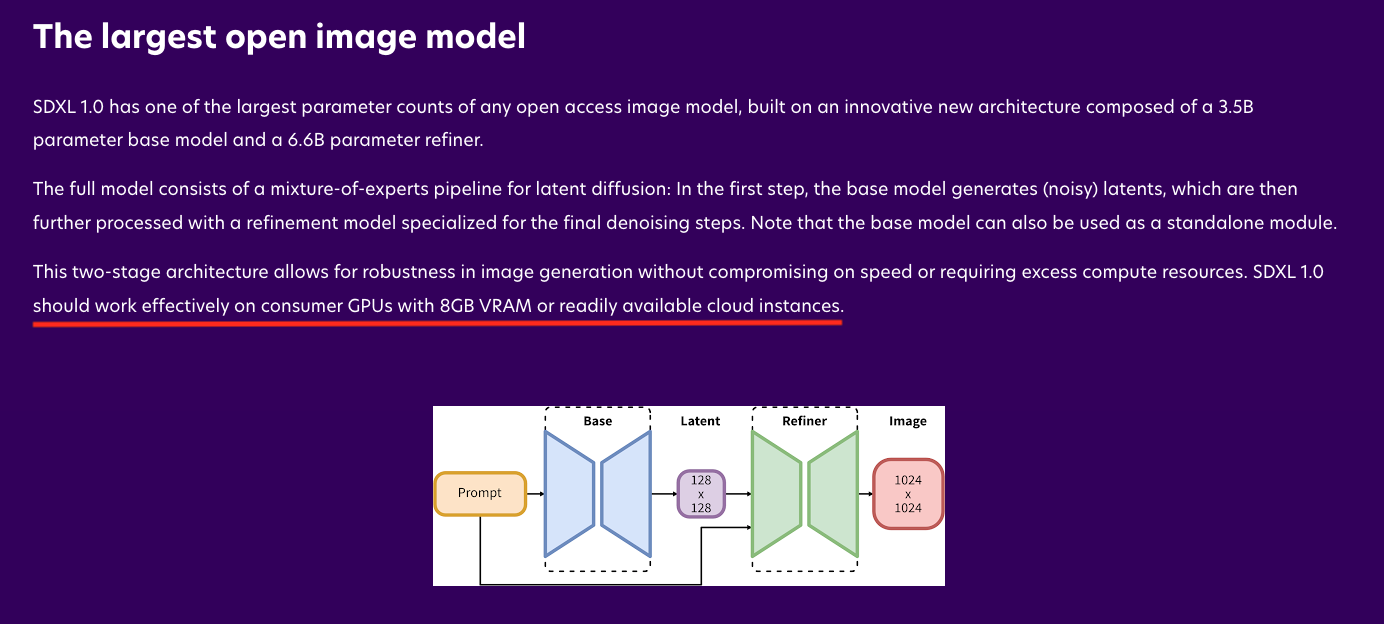
Stable Diffusion 免费升级 SDXL 1.0,哪些新特性值得关注?体验如何?5 分钟带你体验!
一、引言 7 月 26 日,Stability AI 发布了 SDXL 1.0,号称目前为止,最厉害的开放式图像生成大模型。 它到底有没有网上说的那么炸裂?真的已经实现了像 midjourney 一样 靠嘴出图 的功能吗?相对于之前的版本,…...

【广州华锐互动】煤矿设备AR远程巡检系统实现对井下作业的远程监控和管理
煤矿井下作业环境复杂,安全隐患较多。传统的巡检方式存在诸多弊端,如巡检人员难以全面了解井下情况,巡检效率低下,安全隐患难以及时发现和整改等。为了解决这些问题,提高煤矿安全生产水平,越来越多的企业开…...

C语言与Java语言传输数据 需要转位
在Java语言中,可以通过将整数反转并修改字节顺序来实现低位转高位的转换。下面是一个示例代码,可以将一个整数从低位转高位: public static int toHH(int n) {byte[] bytes ByteBuffer.allocate(4).putInt(n).array();for (int i 0; i <…...

Framework开发——系统默认语言修改
Android 系统原版默认的语言为英文,但是对于中国大陆 Android 产品厂商来说,我们定制系统可能需要用户一开机就是简体中文。所以把 Android 系统出厂设置为简体中文对于 Android 系统产品化非常重要,我们可以通过修改系统属性来达到默认语言的作用。本文主要是在 Android 11…...
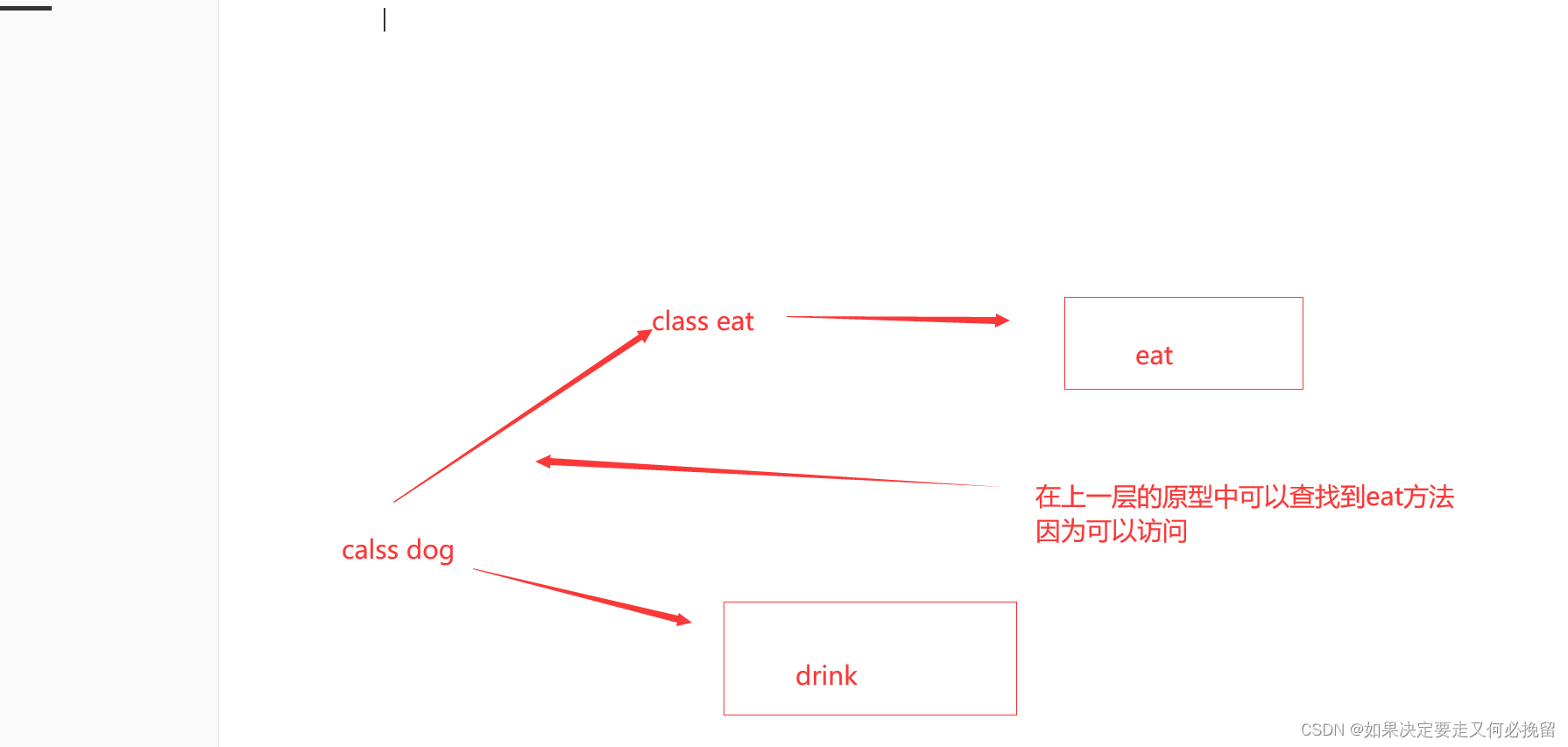
浅谈原型链
一.在掌握原型链之前首先要了解这三点 1.每个函数都有prototype这个属性我们称为原型对象 2.每个对象都有__proto__这个属性 3.对象的__proto__可以访问原型对象上的方法和变量,如果访问不了,就会向上进行查找,直到找不到为止,会出现报错的情况l。 二.例子 1.代码: let arr …...
合宙Air724UG LuatOS-Air LVGL API控件-截屏(Screenshots)
截屏(Screenshots) 分 享导出pdf 截屏功能,core版本号要>3211 示例代码 -- 创建图片控件img lvgl.img_create(lvgl.scr_act(), nil)-- 设置图片显示的图像lvgl.img_set_src(img, "/lua/test.png")-- 图片居中lvgl.obj_align(…...
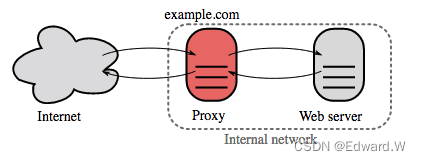
【系统设计系列】 负载均衡和反向代理
系统设计系列初衷 System Design Primer: 英文文档 GitHub - donnemartin/system-design-primer: Learn how to design large-scale systems. Prep for the system design interview. Includes Anki flashcards. 中文版: https://github.com/donnemart…...

Halcon实现3维点云平面拟合
Halcon实现3维点云平面拟合 function main()WindowHandle open_window()ObjectModel3D load_3D_model("1.om3")ObjectModel3DSelected remove_noise(ObjectModel3D)[X, Y, Z] extract_coordinates(ObjectModel3DSelected)[NX, NY, NZ, C] fit_plane(X, Y, Z)vi…...

安全学习DAY23_CookieSessionToken
文章目录 Cookie和Session的区别Token的作用 Cookie和Session的区别 Cookie和Session都是用来在Web应用程序中跟踪用户状态的机制 1、存储位置不同: Cookie是存储在客户端(浏览器)上的,而Session是存储在服务器端的。 2、安全…...

C++ map clear内存泄漏问题
map值存的是指针 map自带的clear()函数会清空map里存储的所有内容,但如果map值存储的是指针,则里面的值不会被清空,会造成内存泄漏,所以值为指针的map必须用迭代器清空。 使用erase迭代删除 迭代器删除值为指针的map,…...
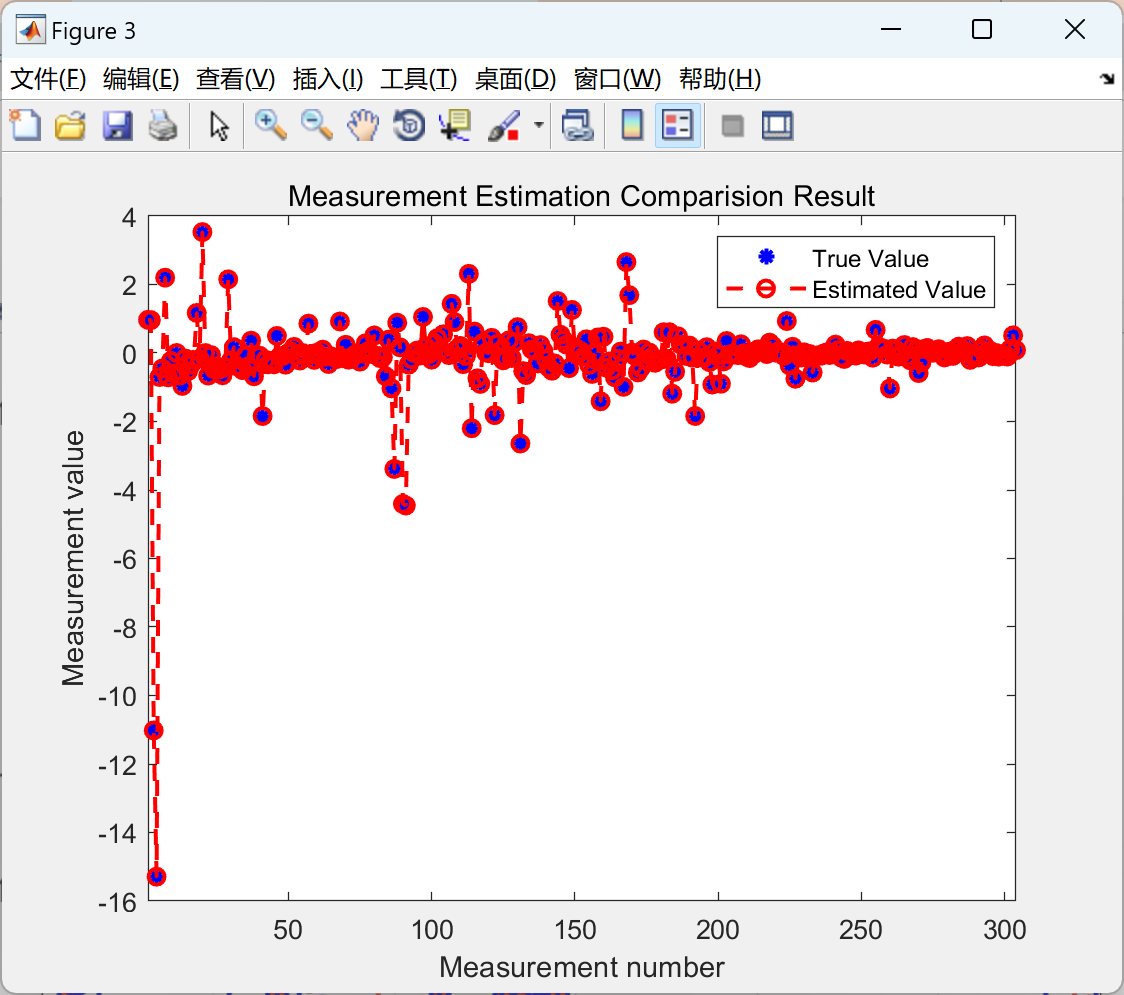
【鲁棒电力系统状态估计】基于投影统计的电力系统状态估计的鲁棒GM估计器(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
