数据结构-时间复杂度/空间复杂度
Hello,好久没有更新了哦,已经开始学习数据结构了,这篇文章呢就是对刚学数据结构所接触到的时间复杂度进行一个分享哦,如果有错误之处,大家记得拍拍我哦~
既然要讨论时间/空间复杂度,那我们就得知道时间/空间复杂度是什么,那到底什么是时间复杂度,什么是空间复杂度呢?
一、时间复杂度
时间复杂度:它是一个函数,这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用O()来表示,不包括这个函数的低价项和首项系数。一个算法所花费的时间与其中语句的执行次数成正比例,那么,算法中的基本操作的执行次数就是算法的时间复杂度。
理解:算法的时间复杂度它是一个函数,其定量的描述了该算法的运行时间。但是,仔细一想,一个算法执行所消耗的时间,从理论上来说的话,它是不可以算出来的,只有在你把程序放在机器上跑起来时,我们才能够知道该算法在整个执行的过程中所消耗的时间。
说这么多,其实用一句话总结:就是找到某条基本语句与问题规模N之间的数学表达式,也就是算出了该算法的时间复杂度。
注:时间复杂度通常用O()来表示。
常见的有:O(1),O(n),O(logn),O(nlogn),O(n^2)等
下面详细介绍一下:
O(1):常数时间复杂度。这类可以说明算法的执行时间不随输入规模的增大而增长。比如,数组的访问,哈希表的查找(后期会更)。
O(n):线性时间复杂度。这类可以说明算法的执行时间随输入规模的增大而增长,其增长速度与输入规模成正比。比如,数组的遍历,简单查找等。
O(logn):对数时间复杂度。这类可以说明算法的执行时间随输入规模的增大而增长。
O(nlogn):线性对数时间复杂度。这类可以说明算法的执行时间随着输入规模的增大而增长,但增长速度比线性快。比如,归并排序,快速排序等。
O(n^2):平方时间复杂度。这类可以说明算法的执行速度随着输入规模的增大而增长,且增长速度很快。比如,冒泡排序,选择排序等。
说明:这里提到的排序后面会更新的,大家在这里先听听哦,这里主要是掌握对时间复杂度的理解。
举个例子:
大家看这段代码:
// 请计算一下Func1中++count语句总共执行了多少次?
void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i){for (int j = 0; j < N; ++j){++count;}}for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}

算法的时间复杂度分为:
(1)最好时间复杂度:指的是算法计算量可能达到的最小值。
(2)最坏时间复杂度:指的是算法计算量可能达到的最大值。
(3)平均时间复杂度:指算法在所有可能情况下,按照输入实例以等概率出现时,算法计算量的加权平均值。
时间复杂度主要衡量一个算法的运行速度的快慢,空间复杂度主要衡量一个算法运行所需要的额外空间。
二、空间复杂度
阶乘递归的空间复杂度是O(N);

b:计算冒泡排序的空间复杂度
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (int end = n; end > 0; --end){int exchange = 0;for (int i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}思路:重复走过要排序的数列,一次比较两个元素,如果它们的顺序不太对劲,就把它们错误的顺序交换过来。这个“工作”是重复的进行知道不再需要交换,换句话说这个数列已经排序完成了。
这里,冒泡排序的辅助变量只是一个临时变量,而且其不会随着排序规模的扩大而因此改变,所以它的空间复杂度为O(1)。
不过,这里要提一嘴的是,对于算法的性能,需要从时间和空间的使用情况来评价。一个好的算法,应该是同时具备时间复杂度和空间复杂度都较低的特性,但是,从实际情况来看的话,对于某个算法问题,要想使得时间复杂度和空间复杂度都优化是蛮困难的。如果说降低时间复杂度的话,那么往往会是它的空间复杂度提高。所以,在通常情况下,在算法设计的过程当中,一般会通过空间换时间的做法,牺牲一部分计算机存储空间,从而来提升整个算法的运行速度。
好啦,关于数据结构中关于 时间复杂度和空间复杂度的介绍先到这里啦,后期有时间的话还会举一些更为详细的例子和大家一起进步~
看到这里,支持一下小编叭~ 如果有错误之处,大家记得评论区留言吖~
相关文章:

数据结构-时间复杂度/空间复杂度
Hello,好久没有更新了哦,已经开始学习数据结构了,这篇文章呢就是对刚学数据结构所接触到的时间复杂度进行一个分享哦,如果有错误之处,大家记得拍拍我哦~ 既然要讨论时间/空间复杂度,那我们就得知道时间/空…...

英语写作中“展示”、“表明”demonstrate、show、indicate、illustrate的用法
一、demonstrate、show、indicate在论文写作中主要用法是:demonstrate/show/indicate 从句: Sb./Sth. demonstrates/shows/indicates that ……从句中一般表达事实、观点和结论等。 例句: The authors demonstrated/showed/indicated that…...
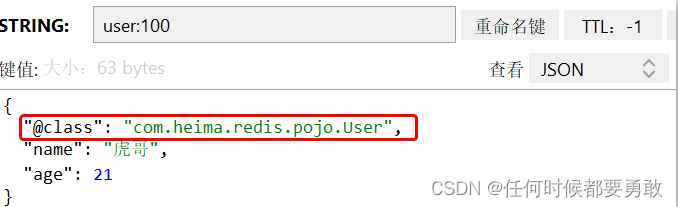
Redis的java客户端
在Redis官网中提供了各种语言的客户端,地址:https://redis.io/resources/clients/ redis的java客户端 https://redis.io/resources/clients/#java 1.jedis使用 引入依赖 <dependency><groupId>redis.clients</groupId><artifac…...
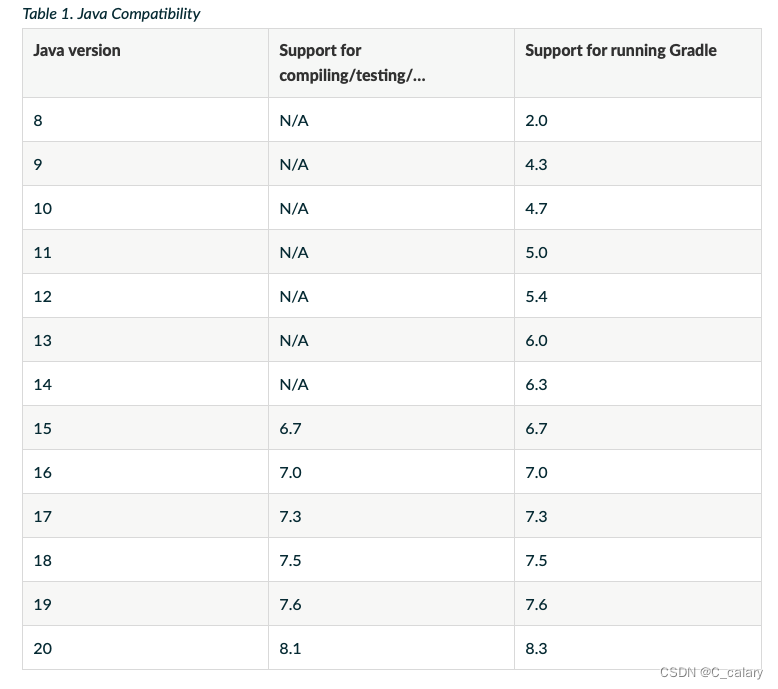
Android环境配置笔记
文章目录 一、各环境文档二、参考 一、各环境文档 Gradle官方的兼容性文档:Java Compatibility 更新日期:2023.9.12 Android Gradle插件版本:Android Gradle Plugin 二、参考 参考文章:Android问题记录...

element-table 行的拖拽更改顺序(无需下载sortableJs
样例展示:vueelement 通过阅读element文档我们发现element并不提供拖拽相关的api 本博客通过element提供的行类名 注册函数 实现行与行的拖拽 1.设置el-table 的行样式类名 这里是用的是 function <el-table:data"outputData":row-class-name&qu…...
Docker部署jenkins
目录 一、jenkins原理二、Docker部署jenkins1.下载jenkins镜像文件2.查看下载的jenkins镜像3.创建Jenkins挂载目录并授权权限4.创建并启动Jenkins容器5.查看jenkins是否启动成功6.查看docker容器日志7.配置镜像加速8.访问Jenkins页面,输入ip地址加上9000端口9.获取管…...
从0到1学会Git(第三部分):Git的远程仓库链接与操作
写在前面:前面两篇文章我们已经学会了git如何在本地进行使用,这篇文章将讲解如何将本地的git仓库和云端的远程仓库链接起来并使用 为什么要使用远程仓库:因为我们需要拷贝我们的代码给别人以及进行协同开发,就需要有一个云端仓库进行代码的存储和同步&a…...
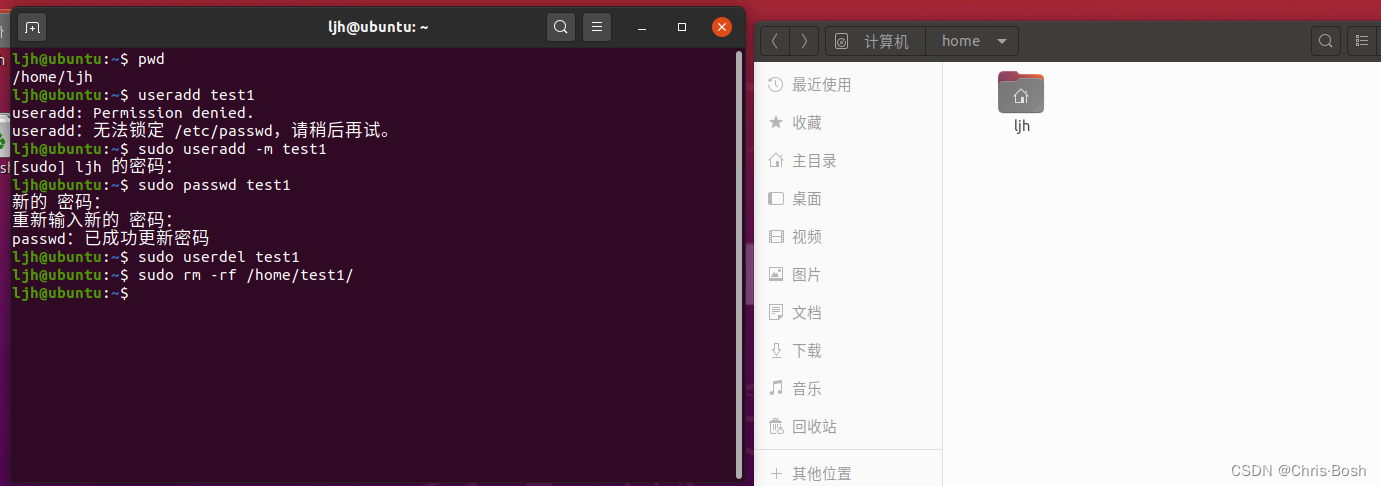
虚拟机Ubuntu操作系统常用终端命令(1)(详细解释+详细演示)
虚拟机Ubuntu操作系统常用终端命令 本篇讲述了Ubuntu操作系统常用的三个功能,即归档,软链接和用户管理方面的相关知识。希望能够得到大家的支持。 文章目录 虚拟机Ubuntu操作系统常用终端命令二、使用步骤1.归档1.1创建档案包1.2还原档案包1.3归档并压缩…...
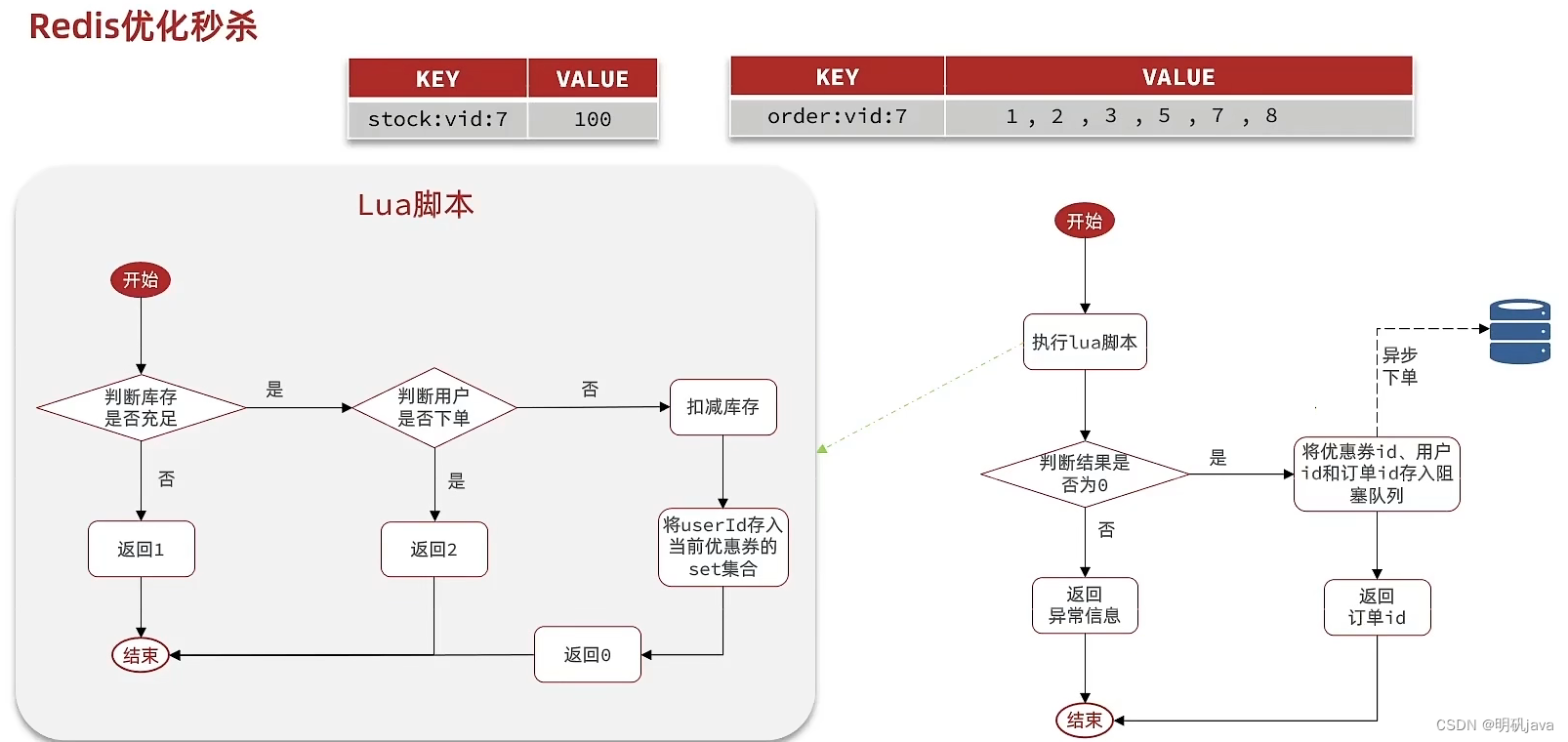
redis实战-redis实现异步秒杀优化
秒杀优化-异步秒杀思路 未优化的思路 当用户发起请求,此时会请求nginx,nginx会访问到tomcat,而tomcat中的程序,会进行串行操作,分成如下几个步骤 1、查询优惠卷 2、判断秒杀库存是否足够 3、查询订单 4、校验是否是一…...

Python爬虫-IP隐藏技术与代理爬取
前言 在进行爬虫程序开发和运行时,常常会遇到目标网站的反爬虫机制,最常见的就是IP封禁,这时需要使用IP隐藏技术和代理爬取。 一、IP隐藏技术 IP隐藏技术,即伪装IP地址,使得爬虫请求的IP地址不被目标网站识别为爬虫。…...
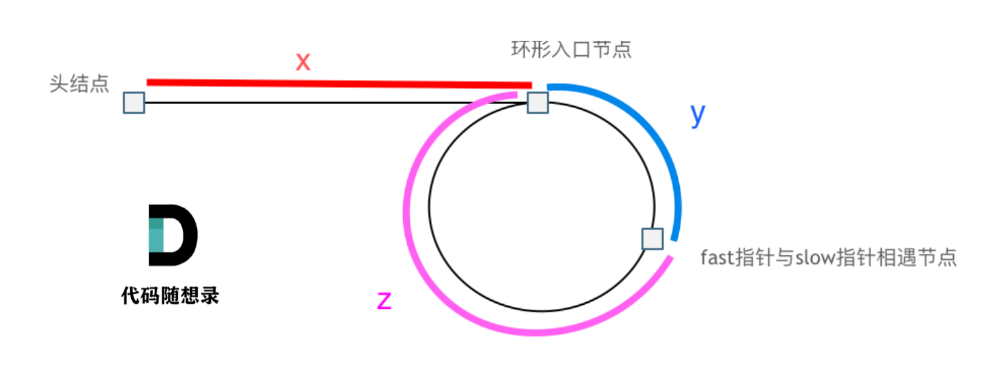
二刷力扣--链表
链表 链表类型: 单链表(可以访问后面的一个节点) 双链表(可以访问前后节点) 循环链表(最后一个节点指向首节点) 在Python中定义单链表节点: class ListNode:def __init__(self, v…...
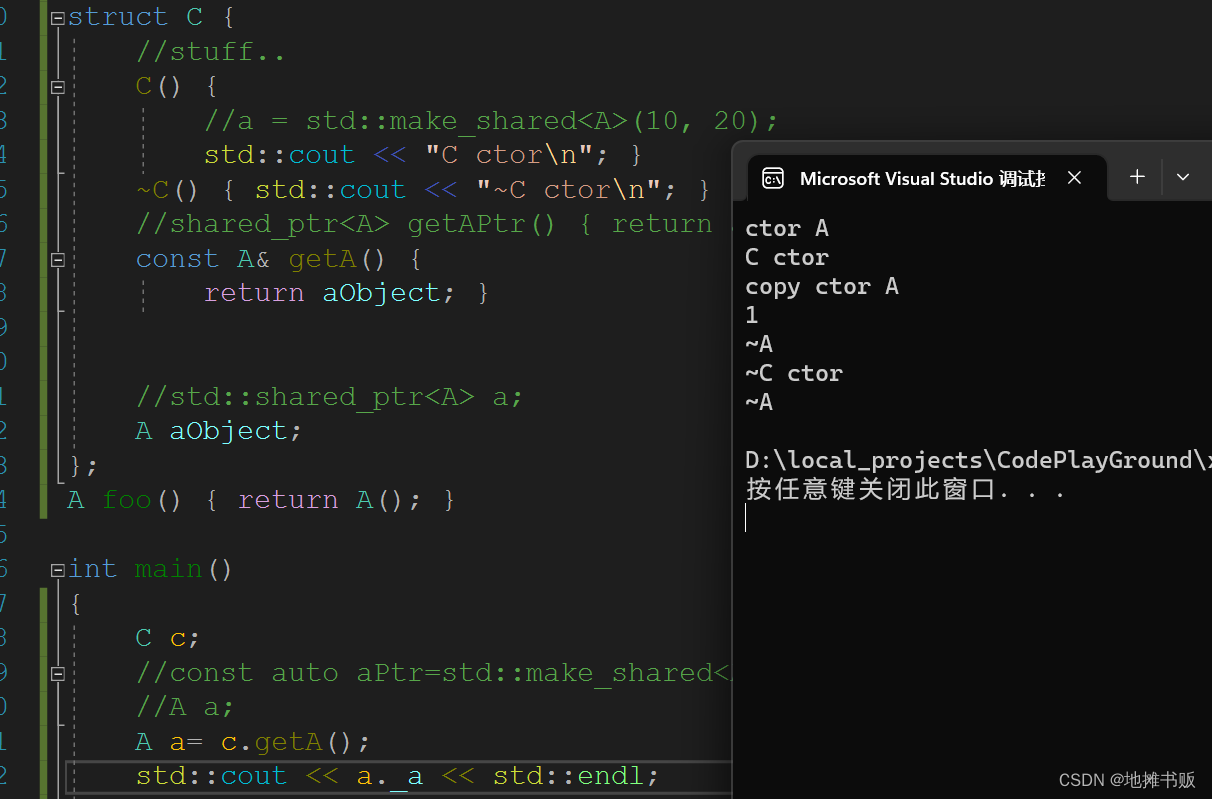
返回值加const ,为了不拷贝得到成员的值,但被赋值的左值也要const
1. getA 函数返回值 什么都不加,也改不了c里面a的指针指向 why?返回成员变量时,会复制一下。 返回成员变量时,一般会赋值一下没有RVO_地摊书贩的博客-CSDN博客 2. getA 函数返回值 加了引用, 就没有复制 3. getA 函数…...

本地如何使用HTTPS进行调试
在现代前端开发中,HTTPS已经成为不可或缺的一部分,因为它在保护用户数据和确保网站安全性方面发挥着关键作用。然而,有时在本地开发过程中启用HTTPS可能会变得有些复杂。在本文中,我们将介绍如何轻松地在本地进行HTTPS调试&#x…...

观察者模式:对象之间的订阅机制
欢迎来到设计模式系列的第十三篇文章!在之前的文章中,我们学习了许多常用的设计模式,今天我们将介绍观察者模式,它是一种行为型设计模式,用于定义对象之间的一对多依赖关系,当一个对象的状态发生变化时&…...
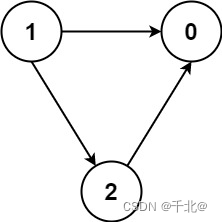
【1462. 课程表 IV】
来源:力扣(LeetCode) 描述: 你总共需要上 numCourses 门课,课程编号依次为 0 到 numCourses-1 。你会得到一个数组 prerequisite ,其中 prerequisites[i] [ai, bi] 表示如果你想选 bi 课程,你…...

Kerberos 身份验证
简介 Kerberos 是一种由 MIT(麻省理工大学)提出的一种基于加密 Ticket 的身份认证协议。它旨在通过使用密钥加密技术为客户端/服务器应用程序提供强身份验证,用于验证用户或主机的标识。。 适用范围:Windows Server 2022、Window…...

R语言贝叶斯METROPOLIS-HASTINGS GIBBS 吉布斯采样器估计变点指数分布分析泊松过程车站等待时间...
原文链接:http://tecdat.cn/?p26578 指数分布是泊松过程中事件之间时间的概率分布,因此它用于预测到下一个事件的等待时间,例如,您需要在公共汽车站等待的时间,直到下一班车到了(点击文末“阅读原文”获取…...

通付盾入选2023年度“上市苗圃工程”重点企业
近日,2023年度苏州工业园区企业上市苗圃工程认定名单公示,江苏通付盾科技有限公司成功入选园区“上市苗圃工程”重点企业。 2023年第一批次苗圃企业认定结果: 企业上市苗圃工程 上市企业是衡量地方综合经济实力的重要标尺,也是区…...

SpringMVC之文件上传下载
SpringMVC是一个基于Java的Web框架,它提供了一套用于构建Web应用程序的开发模型。在SpringMVC中,文件上传和下载是常见的功能之一。 SpringMVC文件上传和下载的介绍: 介绍文件上传: 在SpringMVC中,文件上传功能可以通…...
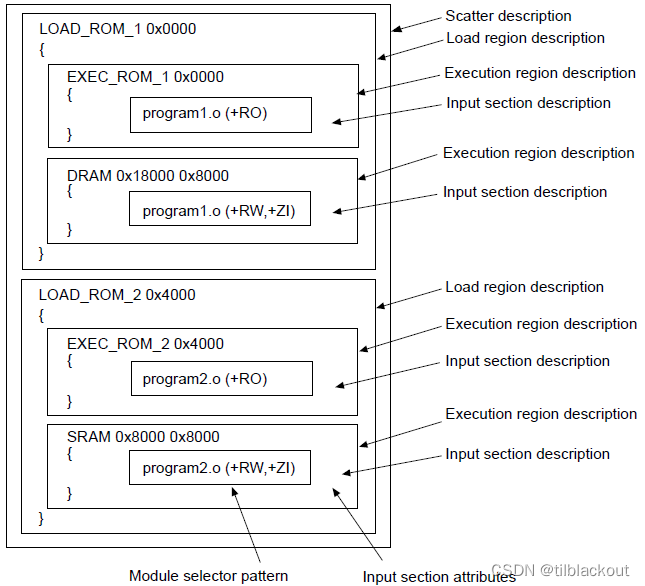
嵌入式IDE(2):KEIL中SCF分散加载链接文件详解和实例分析
在上一篇文章IAR中ICF链接文件详解和实例分析中,我通过I.MX RT1170的SDK中的内存映射关系,分析了IAR中的ICF链接文件的语法。对于MCU编程所使用的IDE来说,IAR和Keil用得比较多,所以这一篇文章就来分析一下Keil的分散文件.scf(scat…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...
