day 53|● 1143.最长公共子序列 ● 1035.不相交的线 ● 53. 最大子序和 动态规划
1143. 最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 。示例 2:
输入:text1 = "abc", text2 = "abc"
输出:3
解释:最长公共子序列是 "abc" ,它的长度为 3 。示例 3:
输入:text1 = "abc", text2 = "def"
输出:0
解释:两个字符串没有公共子序列,返回 0 。
解:
//递推公式:
/*
if text1[i]==text2[j]dp[i][j]=dp[i-1][j-1]+1;
elsedp[i][j]=max(dp[i-1][j],dp[i][j-1]);
*/
class Solution {
public:int longestCommonSubsequence(string text1, string text2) {vector<vector<int>> dp(text1.size()+1,vector<int>(text2.size()+1,0));for(int i=1;i<=text1.size();i++){for(int j=1;j<=text2.size();j++){if(text1[i-1]==text2[j-1])dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}return dp[text1.size()][text2.size()];}
};
- 不相交的线
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足满足:
nums1[i] == nums2[j]
且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
示例 1:
输入:nums1 = [1,4,2], nums2 = [1,2,4]
输出:2
解释:可以画出两条不交叉的线,如上图所示。
但无法画出第三条不相交的直线,因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。示例 2:
输入:nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出:3示例 3:
输入:nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出:2
解:
//我觉得问题还是找最长公共子序列--1143. 最长公共子序列
class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>>dp(nums1.size()+1,vector<int>(nums2.size()+1,0));for(int i=1;i<=nums1.size();i++){for(int j=1;j<=nums2.size();j++){if(nums1[i-1]==nums2[j-1])dp[i][j]=dp[i-1][j-1]+1;elsedp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}return dp[nums1.size()][nums2.size()];}
};
53. 最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。示例 2:
输入:nums = [1]
输出:1示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
解:
/*
设dp[i]为以nums[i]为结尾的最大连续数组和
递归公式:
if(dp[i-1]+nums[i]<nums[i])dp[i]=nums[i];
elsedp[i]=dp[i-1]+nums[i];
遍历dp[i],找出最大值。
同理也是贪心的思想。
*/
class Solution {
public:int maxSubArray(vector<int>& nums) {if(nums.size()==1) return nums[0];vector<int>dp(nums.size(),0);dp[0]=nums[0];int result=nums[0];for(int i=1;i<nums.size();i++){if(dp[i-1]+nums[i]<nums[i])dp[i]=nums[i];else dp[i]=dp[i-1]+nums[i];result=max(dp[i],result);}return result;}
};
相关文章:

day 53|● 1143.最长公共子序列 ● 1035.不相交的线 ● 53. 最大子序和 动态规划
1143. 最长公共子序列 给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。 一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些…...

运维工程师必知的十项Linux常识
1、GNU和GPL GNU计划(又称革奴计划),是由Richard Stallman(理查德斯托曼)在1983年9月27日公开发起的软件集体协作计划。它的目标是创建一套完全的操作系统。GNU也称为软件工程项目。GPL是GNU的通用公共许可证…...

C++ 11 之右值引用和移动语义
文章目录左值引用与右值引用1、左值与右值2、纯右值、将亡值3、左值引用与右值引用4、右值引用和 std::move 使用场景引用限定符移动语义—std::move()完美转发emplace_back 减少内存拷贝和移动总结c11中引用了右值引用和移动语义,可以避免无谓的复制,提…...
【第一章:Spring概述、特点、IOC容器、IOC操作bean管理(基于xml方式)】
第一章:Spring概述、特点、IOC容器、IOC操作bean管理(基于xml方式) 1.Spring是什么? ①Spring是一款主流的java EE 轻量级开源框架。 ②广义的Spring:Spring技术栈,Spring不再是一个单纯的应用框架&#x…...

CSS变量
前端的开发工作中,CSS 是不可或缺的部分;实际工作中,我们通过JavaScript 来进行数据和交互工作,CSS 为用户呈现可视化的界面。有时,CSS 来进行部分交互效果是不是会比 JavaScript 更高效、更省事呢? 一、变…...
.net7窗口编程c#2022实战(1)-zip压缩精灵(1)
目录 创建ZIP精灵项目拖控件OpenFileDialog 类压缩与解压缩编写我们自己的代码其它参考内容创建ZIP精灵项目 VS2022中新建项目。 为窗体取一个标题名称 拖控件 左边工具栏里选择控件 拖三个按钮控件和一个listbox控件...
云计算|OpenStack|使用VMware安装华为云的R006版CNA和VRM
前言: FusionCompute架构 (CNA、VRM) CNA(ComputingNode Agent):计算节点代理VNA虚拟节点代理,部署在CNA上,实施计算、存储、网络的虚拟化的配置管理。VRM(Virtual Resource Manager):虚拟资源管理器 VNA可以省略不安装 本次实验使用的是V…...

中央一号文件首提“即时零售”,县域掀起消费业态新风潮
经过几年的探索,即时零售已经逐步走向成熟,并开始向三四线城市以及乡镇城市渗透。 过去一年,京东、美团、阿里争先布局即时零售市场,完善即时配送网络、培养用户消费习惯,即时零售订单迎来了骤增。2022年下半年&#…...

python多线程编程
Python多线程编程中常用方法: 1、join()方法:如果一个线程或者在函数执行的过程中调用另一个线程,并且希望待其完成操作后才能执行,那么在调用线程的时就可以使用被调线程的join方法join([timeout]) timeout:可选参数…...

小熊电器:精品与创意,走上“顶流之路”的两把“宝剑”
回顾2022年,小家电市场降温趋势明显,业绩表现整体低迷,如主打高端路线的北鼎,去年8亿元的营收出现个位数下滑,归母净利润同比下降超56%;苏泊尔营收也出现微降,归母净利润预计同比增长不到10%。而…...
如何描述元素与元素间的逻辑关系?
逻辑结构反映的是数据元素之间的关系,它们与数据元素在计算机中的存储位置无关,是数据结构在用户面前所呈现的形式。根据不同的逻辑结构来分,数据结构可分为集合、线性结构、树形结构和图形结构4种形式,接下来分别进行简要介绍。 …...
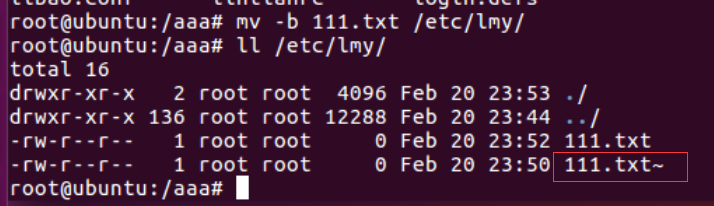
【3】linux命令每日分享——mv改名或移动
大家好,这里是sdust-vrlab,Linux是一种免费使用和自由传播的类UNIX操作系统,Linux的基本思想有两点:一切都是文件;每个文件都有确定的用途;linux涉及到IT行业的方方面面,在我们日常的学习中&…...

【2023最火教程】Python性能测试框架Locust实战教程(建议收藏)
01、认识Locust Locust是一个比较容易上手的分布式用户负载测试工具。它旨在对网站(或其他系统)进行负载测试,并确定系统可以处理多少个并发用户,Locust 在英文中是 蝗虫 的意思:作者的想法是在测试期间,放…...
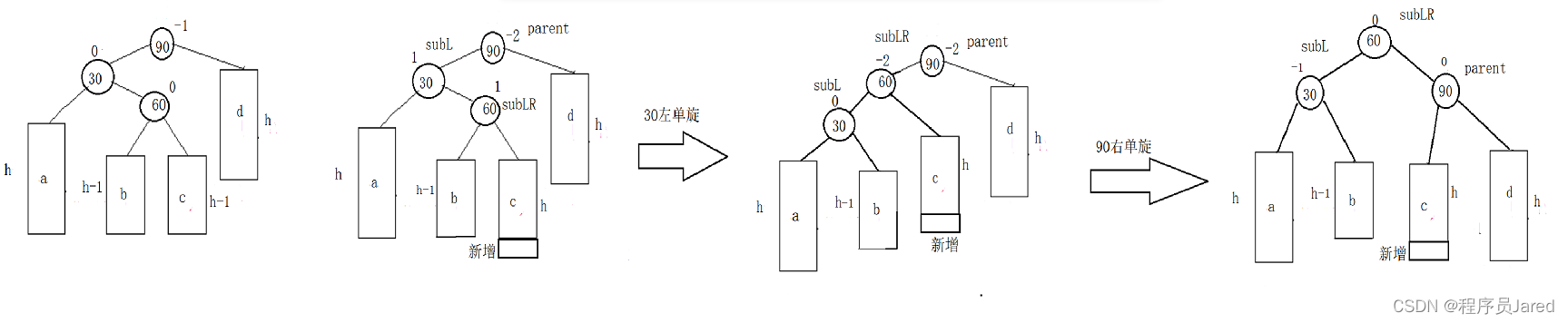
深入浅出C++ ——手撕AVL树
文章目录前言一、AVL 树介绍二、AVL树节点的定义三、AVL树的插入四、AVL树的旋转五、AVL树的验证六、AVL树的删除七、AVL树的性能八、AVL树的实现前言 在前面的文章中介绍了map / multimap / set / multiset 容器,这几个容器的底层都是按照二叉搜索树来实现的。但是…...
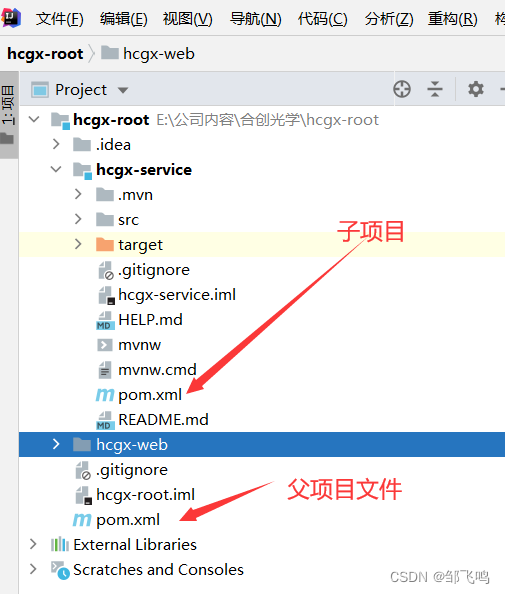
将多个springboot项目的pom.xml文件整合
将多个springboot项目的pom.xml文件整合 0.0、前因 刚入公司敲代码时、发现一个项目中会包含多个子项目、每个子项目会代表一个功能模块、这属实是把我这个菜鸟惊叹到了。而这种分而治之的方式也引申出一个问题:各子项目的依赖如何统一管理? 我…...

【Unity实战100例】Unity串口通讯的消息接收解析和发送指令
目录 一.串口通信介绍 1.串口通信 2.名词介绍 1.上位机: 2.下位机: 3.串行端口...

资源消耗降低 90%,速度提升 50%,解读 Apache Doris Compaction 最新优化与实现
背景LSM-Tree( Log Structured-Merge Tree)是数据库中最为常见的存储结构之一,其核心思想在于充分发挥磁盘连续读写的性能优势、以短时间的内存与 IO 的开销换取最大的写入性能,数据以 Append-only 的方式写入 Memtable、达到阈值…...
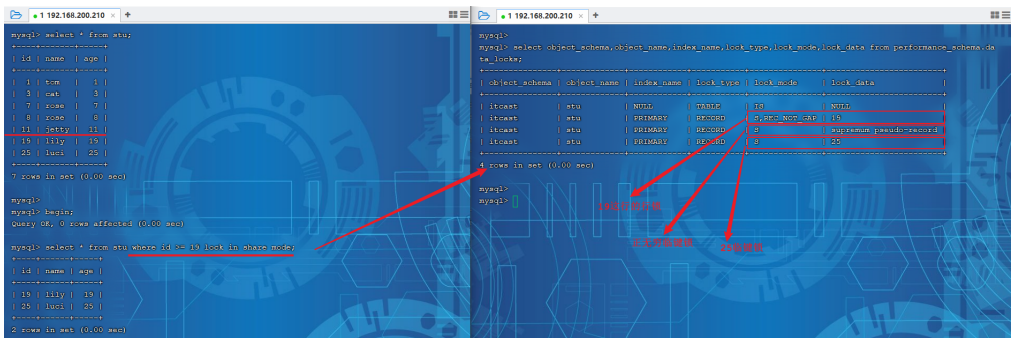
【Mysql】 锁
【Mysql】 锁 文章目录【Mysql】 锁1. 锁1.1 概述1.2 全局锁1.2.1 介绍1.2.2 语法1.2.2.1 加全局锁1.2.2.2 数据备份1.2.2.3 释放锁1.2.3 特点1.3 表级锁1.3.1 介绍1.3.2 表锁1.3.3 元数据锁1.3.4 意向锁1.4 行级锁1.4.1 介绍1.4.2 行锁1.4.3 间隙锁&临键锁1. 锁 1.1 概述…...

Android 流量统计
Android 流量统计最近项目上有一个应用流量统计的功能需要实现,在此总结一下 流量统计架构 在Android9.0之前,流量监控是基于xt_qtaguid模块的,通过读取/proc/net/xt_qtaguid/stats文件内容进行解析获取对应流量数据。 Android9.0之后&…...
如何保证数据的安全?对称和非对称加密,身份认证,摘要算法,数字证书等傻傻分不清?波哥图解带你彻底掌握
支付安全 1.基础概念 明文:加密前的消息叫“明文”(plain text) 密文:加密后的文本叫“密文”(cipher text) 密钥:只有掌握特殊“钥匙”的人,才能对加密的文本进行解密,…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...
