支持向量机SVM详细原理,Libsvm工具箱详解,svm参数说明,svm应用实例,神经网络1000案例之15
目录
支持向量机SVM的详细原理
SVM的定义
SVM理论
Libsvm工具箱详解
简介
参数说明
易错及常见问题
SVM应用实例,基于SVM的股票价格预测
支持向量机SVM的详细原理
SVM的定义
支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;SVM还包括核技巧,这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化,可形式化为一个求解凸二次规划的问题,也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。
(1)支持向量机(Support Vector Machine, SVM)是一种对数据进行二分类的广义线性分类器,其分类边界是对学习样本求解的最大间隔超平面。
(2)SVM使用铰链损失函数计算经验风险并在求解系统中加入了正则化项以优化结构风险,是一个具有稀疏性和稳健性的分类器 。
(3)SVM可以通过引入核函数进行非线性分类。
SVM理论
1,线性可分性

2,损失函数


3,核函数


Libsvm工具箱详解
简介
LIBSVM是台湾大学林智仁(Lin Chih-Jen)教授等开发设计的一个简单、易于使用和快速有效的SVM模式识别与回归的软件包,他不但提供了编译好的可在Windows系列系统的执行文件,还提供了源代码,方便改进、修改以及在其它操作系统上应用;该软件对SVM所涉及的参数调节相对比较少,提供了很多的默认参数,利用这些默认参数可以解决很多问题;并提供了交互检验(Cross Validation)的功能。该软件可以解决C-SVM、ν-SVM、ε-SVR和ν-SVR等问题,包括基于一对一算法的多类模式识别问题。
主要参数说明
Options:可用的选项即表示的涵义如下
-s svm类型:SVM设置类型(默认0)
0 – C-SVC
1 --v-SVC
2 – 一类SVM
3 – e -SVR
4 – v-SVR
-t 核函数类型:核函数设置类型(默认2)
0 – 线性:u’v
1 – 多项式:(ru’v + coef0)^degree
2 – RBF函数:exp(-r|u-v|^2)
3 –sigmoid:tanh(ru’v + coef0)
-d degree:核函数中的degree设置(针对多项式核函数)(默认3)
-g r(gama):核函数中的gamma函数设置(针对多项式/rbf/sigmoid核函数)(默认1/ k)
-r coef0:核函数中的coef0设置(针对多项式/sigmoid核函数)((默认0)
-c cost:设置C-SVC,e -SVR和v-SVR的参数(损失函数)(默认1)
-n nu:设置v-SVC,一类SVM和v- SVR的参数(默认0.5)
-p p:设置e -SVR 中损失函数p的值(默认0.1)
-m cachesize:设置cache内存大小,以MB为单位(默认40)
-e eps:设置允许的终止判据(默认0.001)
-h shrinking:是否使用启发式,0或1(默认1)
-wi weight:设置第几类的参数C为weight*C(C-SVC中的C)(默认1)
-v n: n-fold交互检验模式,n为fold的个数,必须大于等于2
其中-g选项中的k是指输入数据中的属性数。option -v 随机地将数据剖分为n部分并计算交互检验准确度和均方根误差。以上这些参数设置可以按照SVM的类型和核函数所支持的参数进行任意组合,如果设置的参数在函数或SVM类型中没有也不会产生影响,程序不会接受该参数;如果应有的参数设置不正确,参数将采用默认值。
具体对应解释如下:
svm类别
指定SVM的类型,下面是可能的取值:
CvSVM::C_SVC C类支持向量分类机。 n类分组 (n \geq 2),允许用异常值惩罚因子C进行不完全分类。
CvSVM::NU_SVC \nu类支持向量分类机。n类似然不完全分类的分类器。参数为 \nu 取代C(其值在区间【0,1】中,nu越大,决策边界越平滑)。
CvSVM::ONE_CLASS 单分类器,所有的训练数据提取自同一个类里,然后SVM建立了一个分界线以分割该类在特征空间中所占区域和其它类在特征空间中所占区域。
CvSVM::EPS_SVR \epsilon类支持向量回归机。训练集中的特征向量和拟合出来的超平面的距离需要小于p。异常值惩罚因子C被采用。
CvSVM::NU_SVR \nu类支持向量回归机。 \nu 代替了 p。
kernel_type –
SVM的内核类型,下面是可能的取值:
CvSVM::LINEAR 线性内核。没有任何向映射至高维空间,线性区分(或回归)在原始特征空间中被完成,这是最快的选择。K(x_i, x_j) = x_i^T x_j.
CvSVM::POLY 多项式内核: K(x_i, x_j) = (\gamma x_i^T x_j + coef0)^{degree}, \gamma > 0.
CvSVM::RBF 基于径向的函数,对于大多数情况都是一个较好的选择: K(x_i, x_j) = e^{-\gamma ||x_i - x_j||^2}, \gamma > 0.
CvSVM::SIGMOID Sigmoid函数内核:K(x_i, x_j) = \tanh(\gamma x_i^T x_j + coef0).
degree – 内核函数(POLY)的参数degree。
gamma – 内核函数(POLY/ RBF/ SIGMOID)的参数\gamma。
coef0 – 内核函数(POLY/ SIGMOID)的参数coef0。
Cvalue – SVM类型(C_SVC/ EPS_SVR/ NU_SVR)的参数C。
nu – SVM类型(NU_SVC/ ONE_CLASS/ NU_SVR)的参数 \nu。
p – SVM类型(EPS_SVR)的参数 \epsilon。
class_weights – C_SVC中的可选权重,赋给指定的类,乘以C以后变成 class_weights_i * C。所以这些权重影响不同类别的错误分类惩罚项。权重越大,某一类别的误分类数据的惩罚项就越大。
term_crit – SVM的迭代训练过程的中止条件,解决部分受约束二次最优问题。您可以指定的公差和/或最大迭代次数。
易错及调参注意事项
1,分类和回归容易搞错,分类-s参数为1,回归-s参数为1
2,bestc参数分类的时候调小,回归的时候调大。
3,安装libsvm参数的时候,工具箱自带的参数容易和matlab自带的冲突,要做好协调
SVM应用实例
基于SVM的股票价格预测MATLAB代码
tic;
close all;
clear;
clc;
format compact;
%% 数据的提取和预处理
% 载入测试数据上证指数(1990.12.19-2009.08.19)
% 数据是一个4579*6的double型的矩阵,每一行表示每一天的上证指数
% 6列分别表示当天上证指数的开盘指数,指数最高值,指数最低值,收盘指数,当日交易量,当日交易额.
load chapter14_sh.mat;
% 提取数据
[m,n] = size(sh);
ts = sh(2:m,1);
tsx = sh(1:m-1,:);
% 画出原始上证指数的每日开盘数
figure;
plot(ts,‘LineWidth’,2);
title(‘上证指数的每日开盘数(1990.12.20-2009.08.19)’,‘FontSize’,12);
xlabel(‘交易日天数(1990.12.19-2009.08.19)’,‘FontSize’,12);
ylabel(‘开盘数’,‘FontSize’,12);
grid on;
% 数据预处理,将原始数据进行归一化
ts = ts’;
tsx = tsx’;
% mapminmax为matlab自带的映射函数
% 对ts进行归一化
[TS,TSps] = mapminmax(ts,1,2);
% 画出原始上证指数的每日开盘数归一化后的图像
figure;
plot(TS,‘LineWidth’,2);
title(‘原始上证指数的每日开盘数归一化后的图像’,‘FontSize’,12);
xlabel(‘交易日天数(1990.12.19-2009.08.19)’,‘FontSize’,12);
ylabel(‘归一化后的开盘数’,‘FontSize’,12);
grid on;
% 对TS进行转置,以符合libsvm工具箱的数据格式要求
TS = TS’;
% mapminmax为matlab自带的映射函数
% 对tsx进行归一化
[TSX,TSXps] = mapminmax(tsx);
% 对TSX进行转置,以符合libsvm工具箱的数据格式要求
TSX = TSX’;
%% 选择回归预测分析最佳的SVM参数c&g
% 首先进行粗略选择:
[bestmse,bestc,bestg] = SVMcgForRegress(TS,TSX,-8,8,-8,8);
% 打印粗略选择结果
disp(‘打印粗略选择结果’);
str = sprintf( ‘Best Cross Validation MSE = %g Best c = %g Best g = %g’,bestmse,bestc,bestg);
disp(str);
% 根据粗略选择的结果图再进行精细选择:
[bestmse,bestc,bestg] = SVMcgForRegress(TS,TSX,-4,4,-4,4,3,0.5,0.5,0.05);
% 打印精细选择结果
disp(‘打印精细选择结果’);
str = sprintf( ‘Best Cross Validation MSE = %g Best c = %g Best g = %g’,bestmse,bestc,bestg);
disp(str);
%% 利用回归预测分析最佳的参数进行SVM网络训练
cmd = ['-c ', num2str(bestc), ’ -g ‘, num2str(bestg) , ’ -s 3 -p 0.01’];
model = svmtrain(TS,TSX,cmd);
%% SVM网络回归预测
[predict,mse] = svmpredict(TS,TSX,model);
predict = mapminmax(‘reverse’,predict’,TSps);
predict = predict’;
% 打印回归结果
str = sprintf( ‘均方误差 MSE = %g 相关系数 R = %g%%’,mse(2),mse(3)*100);
disp(str);
%% 结果分析
figure;
hold on;
plot(ts,‘-o’);
plot(predict,‘r-^’);
legend(‘原始数据’,‘回归预测数据’);
hold off;
title(‘原始数据和回归预测数据对比’,‘FontSize’,12);
xlabel(‘交易日天数(1990.12.19-2009.08.19)’,‘FontSize’,12);
ylabel(‘开盘数’,‘FontSize’,12);
grid on;
figure;
error = predict - ts’;
plot(error,‘rd’);
title(‘误差图(predicted data - original data)’,‘FontSize’,12);
xlabel(‘交易日天数(1990.12.19-2009.08.19)’,‘FontSize’,12);
ylabel(‘误差量’,‘FontSize’,12);
grid on;
figure;
error = (predict - ts’)./ts’;
plot(error,‘rd’);
title(‘相对误差图(predicted data - original data)/original data’,‘FontSize’,12);
xlabel(‘交易日天数(1990.12.19-2009.08.19)’,‘FontSize’,12);
ylabel(‘相对误差量’,‘FontSize’,12);
grid on;
snapnow;
toc;
%% 子函数 SVMcgForRegress.m
% function [mse,bestc,bestg] = SVMcgForRegress(train_label,train,cmin,cmax,gmin,gmax,v,cstep,gstep,msestep)
% %SVMcg cross validation by faruto
%
% %
% % by faruto
% %Email:patrick.lee@foxmail.com QQ:516667408 http://blog.sina.com.cn/faruto BNU
% %last modified 2010.01.17
% %Super Moderator @ www.ilovematlab.cn
%
% % 若转载请注明:
% % faruto and liyang , LIBSVM-farutoUltimateVersion
% % a toolbox with implements for support vector machines based on libsvm, 2009.
% % Software available at http://www.ilovematlab.cn
% %
% % Chih-Chung Chang and Chih-Jen Lin, LIBSVM : a library for
% % support vector machines, 2001. Software available at
% % http://www.csie.ntu.edu.tw/~cjlin/libsvm
%
% % about the parameters of SVMcg
% if nargin < 10
% msestep = 0.06;
% end
% if nargin < 8
% cstep = 0.8;
% gstep = 0.8;
% end
% if nargin < 7
% v = 5;
% end
% if nargin < 5
% gmax = 8;
% gmin = -8;
% end
% if nargin < 3
% cmax = 8;
% cmin = -8;
% end
% % X:c Y:g cg:acc
% [X,Y] = meshgrid(cmin:cstep:cmax,gmin:gstep:gmax);
% [m,n] = size(X);
% cg = zeros(m,n);
%
% eps = 10^(-4);
%
% bestc = 0;
% bestg = 0;
% mse = Inf;
% basenum = 2;
% for i = 1:m
% for j = 1:n
% cmd = [‘-v ‘,num2str(v),’ -c ‘,num2str( basenum^X(i,j) ),’ -g ‘,num2str( basenum^Y(i,j) ),’ -s 3 -p 0.1’];
% cg(i,j) = svmtrain(train_label, train, cmd);
%
% if cg(i,j) < mse
% mse = cg(i,j);
% bestc = basenum^X(i,j);
% bestg = basenum^Y(i,j);
% end
%
% if abs( cg(i,j)-mse )<=eps && bestc > basenum^X(i,j)
% mse = cg(i,j);
% bestc = basenum^X(i,j);
% bestg = basenum^Y(i,j);
% end
%
% end
% end
% % to draw the acc with different c & g
% [cg,ps] = mapminmax(cg,0,1);
% figure;
% [C,h] = contour(X,Y,cg,0:msestep:0.5);
% clabel(C,h,‘FontSize’,10,‘Color’,‘r’);
% xlabel(‘log2c’,‘FontSize’,12);
% ylabel(‘log2g’,‘FontSize’,12);
% firstline = ‘SVR参数选择结果图(等高线图)[GridSearchMethod]’;
% secondline = [‘Best c=’,num2str(bestc),’ g=‘,num2str(bestg), …
% ’ CVmse=’,num2str(mse)];
% title({firstline;secondline},‘Fontsize’,12);
% grid on;
%
% figure;
% meshc(X,Y,cg);
% % mesh(X,Y,cg);
% % surf(X,Y,cg);
% axis([cmin,cmax,gmin,gmax,0,1]);
% xlabel(‘log2c’,‘FontSize’,12);
% ylabel(‘log2g’,‘FontSize’,12);
% zlabel(‘MSE’,‘FontSize’,12);
% firstline = ‘SVR参数选择结果图(3D视图)[GridSearchMethod]’;
% secondline = [‘Best c=’,num2str(bestc),’ g=‘,num2str(bestg), …
% ’ CVmse=’,num2str(mse)];
% title({firstline;secondline},‘Fontsize’,12);
效果图







结果分析
从效果图看,SVM能很好的实现股票价格的预测,相对于传统的二分类SVM,libsvm工具箱,不仅能实现多分类,还可以实现回归分析,大大扩展了SVM的应用范围,在很多方面,特别小样本难训练的问题的应用方面,SVM拥有特别的优势
相关文章:

支持向量机SVM详细原理,Libsvm工具箱详解,svm参数说明,svm应用实例,神经网络1000案例之15
目录 支持向量机SVM的详细原理 SVM的定义 SVM理论 Libsvm工具箱详解 简介 参数说明 易错及常见问题 SVM应用实例,基于SVM的股票价格预测 支持向量机SVM的详细原理 SVM的定义 支持向量机(support vector machines, SVM)是一种二分类模型&a…...
Mac 上搭建 iOS WebDriverAgent 环境
文章目录Mac环境搭建配置 Xcode 生成 WDA常见问题brew 安装失败Mac环境搭建 macOS 系统电脑:12.6.2 Xcode:14.0.1(xcodebuild -version) appium Desktop:1.21.0 (下载链接) Appium Desktop 1.22.0 ,从该版…...

python学习笔记之例题篇NO.3
获得用户输入的一个整数N,输出N中所出现不同数字的和。 s list(set(list(input())))# ① r…...
【Kubernetes】第七篇 - Service 服务介绍和使用
一,前言 上一篇,通过配置一个 Deployment 对象,在内部创建副本集对象,副本集帮我们创建了 3 个 pod 副本 由于 pod 存在 IP 漂移现象,pod 的创建和重启会导致 IP 变化; 本篇,介绍 Service 服…...
Linux 终端复用器Tmux
目录 Tmux讲解 配置tmux 配置tmux会话 配置tmux窗口(在会话界面进行配置) 配置tmux面板 配置窗口共享同步 Tmux讲解 RHEL5/6/7使用的是screen软件包 RHEL8使用的是tumx软件包(功能更强大,更易用) tmux的三个基本…...

Hadoop集群模式安装(Cluster mode)
1、Hadoop源码编译 安装包、源码包下载地址 Index of /dist/hadoop/common/hadoop-3.3.0为什么要重新编译Hadoop源码? 匹配不同操作系统本地库环境,Hadoop某些操作比如压缩、IO需要调用系统本地库(*.so|*.dll) 修改源码、重构源码 如何…...
PTA L1-054 福到了(详解)
前言:内容包括:题目,代码实现,大致思路,代码解读 题目: “福”字倒着贴,寓意“福到”。不论到底算不算民俗,本题且请你编写程序,把各种汉字倒过来输出。这里要处理的每…...

python -- 魔术方法
魔术方法就算定义在类里面的一些特殊的方法 特点:这些func的名字前面都有两个下划线 __new__方法 相当于一个类的创建一个对象的过程 __init__方法 相当于为这个类创建好的对象分配地址初始化的过程 __del__方法 一个类声明这个方法后,创建的对象如果…...

「JVM 编译优化」提前编译器
1996 年 JDK 1.0 发布,同年 7 月 外挂即时编译器发布(JDK 1.0.2),而 Java 提前编译发布在之后几个月(IBM High Performance Compiler for Java),1998 年 GNU 组织公布 GCC 家族新成员 GNU Compi…...

Golang channel 用法与实现原理
文章目录1.简介2.用法3.三种状态4.实现原理数据结构原理概述5.小结参考文献1.简介 Golang channel 是一种并发原语,用于在不同 goroutine 之间进行通信和同步。本质上,channel 是一种类型安全的 FIFO 队列,它可以实现多个 goroutine 之间的同…...
)
jackson 序列化、反序列化的时候第一个大写单词变成小写了(属性设置不成功)
参考链接:https://www.baeldung.com/jackson-annotations 遇到的问题 之前和第三方对接,返回的接口中的属性名称是拼音字母大写,奇怪,反序列化的时候好多字段都为空,没设置进去。 因为对接前,我先用 IntelliJ IDEA …...

如何判断机器学习数据集是否是线性的
首先,线性和非线性函数之间的区别: 左边是线性函数,右边是非线性函数。 线性函数:可以简单定义为始终遵循以下原则的函数: 输入/输出=常数。 线性方程总是1次多项式(例如x+2y+3=0)。在二维情况下,它们总是形成直线;在其他维度中,它们也可以形成平面、点或超平面。它们的…...

后端基础SQL
SQL基础语法: sql对大小写不敏感,eg: SELECT 等效于 select;select: select用于从表中查找数据,select 列名 from 表名 —> 结果集::仅有查询列的结果表; SELECT * FROM 表名称 ----> 结果集: 查找表的所有数据…...
)
Ubuntu 18.04 上编译和安装内核(内核源码版本)
Ubuntu 18.04 上编译和安装内核(内核源码版本) linux发行版本为,ubuntu18.04。内核版本为5.15.7。其他版本类似。 1.下载内核源代码。可以从官方网站下载最新的内核源代码,也可以使用 Git 命令从 Linux 内核的 Git 仓库中获取最新…...

day 53|● 1143.最长公共子序列 ● 1035.不相交的线 ● 53. 最大子序和 动态规划
1143. 最长公共子序列 给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。 一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些…...

运维工程师必知的十项Linux常识
1、GNU和GPL GNU计划(又称革奴计划),是由Richard Stallman(理查德斯托曼)在1983年9月27日公开发起的软件集体协作计划。它的目标是创建一套完全的操作系统。GNU也称为软件工程项目。GPL是GNU的通用公共许可证…...

C++ 11 之右值引用和移动语义
文章目录左值引用与右值引用1、左值与右值2、纯右值、将亡值3、左值引用与右值引用4、右值引用和 std::move 使用场景引用限定符移动语义—std::move()完美转发emplace_back 减少内存拷贝和移动总结c11中引用了右值引用和移动语义,可以避免无谓的复制,提…...
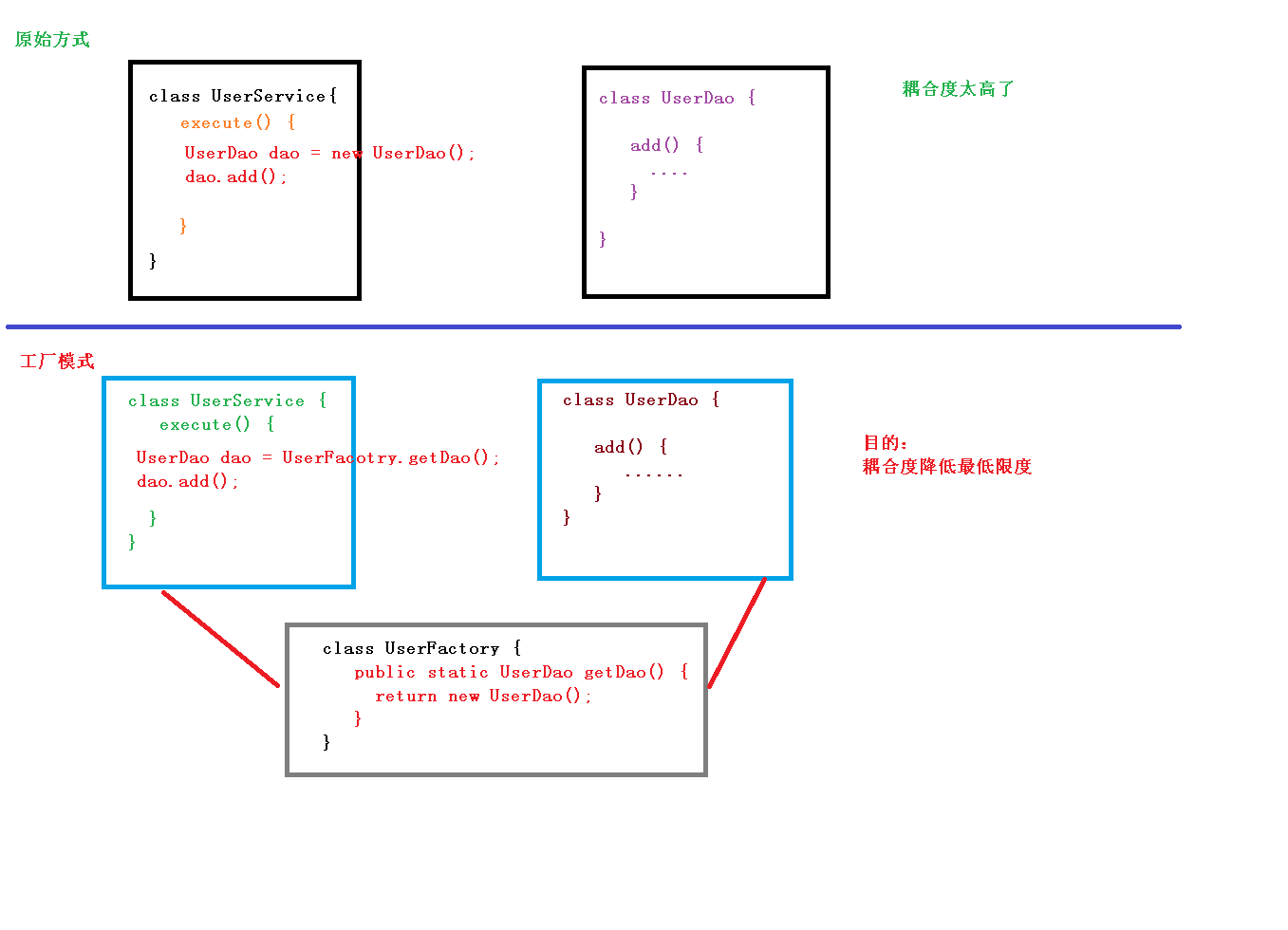
【第一章:Spring概述、特点、IOC容器、IOC操作bean管理(基于xml方式)】
第一章:Spring概述、特点、IOC容器、IOC操作bean管理(基于xml方式) 1.Spring是什么? ①Spring是一款主流的java EE 轻量级开源框架。 ②广义的Spring:Spring技术栈,Spring不再是一个单纯的应用框架&#x…...

CSS变量
前端的开发工作中,CSS 是不可或缺的部分;实际工作中,我们通过JavaScript 来进行数据和交互工作,CSS 为用户呈现可视化的界面。有时,CSS 来进行部分交互效果是不是会比 JavaScript 更高效、更省事呢? 一、变…...
.net7窗口编程c#2022实战(1)-zip压缩精灵(1)
目录 创建ZIP精灵项目拖控件OpenFileDialog 类压缩与解压缩编写我们自己的代码其它参考内容创建ZIP精灵项目 VS2022中新建项目。 为窗体取一个标题名称 拖控件 左边工具栏里选择控件 拖三个按钮控件和一个listbox控件...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...
