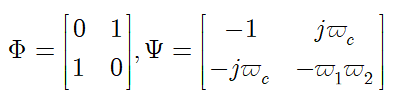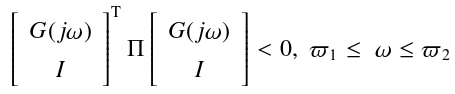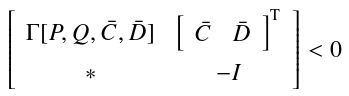线性矩阵不等式(LMI)在控制理论中的应用
目录
(一)Matlab中的LMI处理工具包
(二)为什么LMI成为控制理论领域重要工具?
(三)LMI在与Lyapunov不等式的关系
(1)线性矩阵不等式
(2)线性矩阵不等式系统
(3)舒尔(Schur)补
(四)LMI中常见引理
引理2(广义KYP引理[4])
推论1(广义KYP引理推论[4])
引理3(射影定理[1])
引理4 (Jensen不等式[5,6]
引理5 (Finsler's引理[7]):
参考文献
(一)Matlab中的LMI处理工具包
matlab中有专门求解线性矩阵不等式的工具包YALMIP,可以在官网上下载安装,可参考yalmip安装教程。yalmip只提供了一些基本的LMI求解方法,有更复杂的不等式求解需求可以再安装cplex工具包。关于怎么使用yalmip工具包可参考yalmip代码编写教程。
(二)为什么LMI成为控制理论领域重要工具?
线性矩阵不等式(LMI)技术是分析和综合控制系统的重要工具,尤其是鲁棒控制领域,主要因素有以下三个[1]:
- 对于经典的控制方法,LMI技术的优点就是操作简单。在LMI技术出现以前,人们通过求解Ricaati方程来设计最优控制器,但是Ricaati方程求解很难。而LMI技术仅需少量的概念和基本原理就能开发出实用的工具(现在我们用YALMIP工具包就能很方便的求解LMI问题)。
- LMI技术提供了控制问题的广泛前景,包括鲁棒性分析,标称H∞,H2和鲁棒控制综合,多目标综合,线性参数变化综合,其中一些无法在古典控制领域中解决处理。
- LMI技术是利用凸优化的强有效的数值工具,并在理论体系上附加上有效的软件工具。
(三)LMI在与Lyapunov不等式的关系
(1)线性矩阵不等式
![]()
![]()
![]()
因此有:
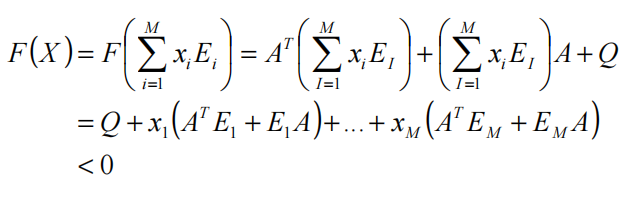
通过这种转化,就得到了一个更为一般的线性矩阵不等式的表达方式。
(2)线性矩阵不等式系统
假设存在多个矩阵不等式:
![]()
总体构成称线性矩阵不等式系统。引进,则
同时成立当且仅当
。因此一个线性矩阵不等式系统也可以用一个单一的线性矩阵不等式表示。
(3)舒尔(Schur)补
在许多一些非线性矩阵不等式转化成线性矩阵不等式的问题中,我们常常用到矩阵的Schur补性质。考虑一个矩阵![]() ,并将S分块:
,并将S分块:
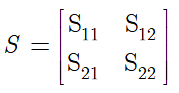
其中是
维的。假定
是非奇异的,则
![]() 称为“
称为“在S中的Sehar补”。以下引理给出了矩阵的Schur补性质。
引理1 Schur补性质
对给定的对称矩阵:
其中
是
维的。以下3个条件是等价的:
(1)
(2)
(3)
(证明方法可参考 俞立的《鲁棒控制——线性矩阵不等式处理方法》 p8页)
在一些控制问题中,经常遇到二次型矩阵不等式[3]:
![]()
其中是给定的适当维数的常数矩阵,
是对称矩阵变量,则应用引理1,可以将上面的矩阵不等式的可行性问题转化成一个等价的矩阵不等式:

的可行性问题,而后者是一个关于矩阵变量P的线性矩阵不等式。
因此在控制问题中,我们经常要设计Lyapunov函数V(t),并为了保证系统稳定性要求,那我们就可以把
这个不等式转化为线性矩阵不等式的形式,并用matlab中的YALMIP直接求解出即可。
(四)LMI中常见引理
引理2(广义KYP引理[4])
给定矩阵
,
以及
,
,且
代表
的零空间,其中
,则不等式
成立,当且仅当存在对称矩阵
以及
,使得
成立,其中
其中*表示矩阵的共轭转置,j是虚数单位,
表示右克罗内克积,即
推论1(广义KYP引理推论[4])
针对线性系统
,
为系统由扰动到控制输出的传递函数,则对于给定的对称矩阵
,下面两个陈述是等价的:
1)有限频域不等式
成立。
2)存在对称矩阵Р和Q满足Q>0,使得
成立,其中
且
表示矩阵
的右上块和右下块,矩阵中*表示其对应块的转置。
引理3(射影定理[1])
对于给定的标量
,矩阵
满足
,当且仅当下面两个条件成立:
引理3(反射影定理[1]):
是给定的正定对称矩阵,不等式
等价于下面的线性矩阵不等式(LMI)求解问题:
式中符号
用以表示矩阵
与其转置的加和,即
。
引理4 (Jensen不等式[5,6]
对于任意正定对称常数矩阵
,标量
满足
,并且存在一个向量
,那么以下不等式成立:
引理5 (Finsler's引理[7]):
令
,
,以及
满足H的秩小于n,rank(H) = r <n.则下列两式等价:
参考文献
【1】Apkarian P,Tuan H D,Bernussou J.Continuous-Time analysis,eigenstructure as-signment,and H2synthesis with enhanced Linear Matrix Inequalities(LMI)char-acterizations[J].IEEE Transactions on Automatic Control,2001,42(12):1941–1946.
【2】《鲁棒控制理论及应用》王娟 张涛 徐国凯
【3】《鲁棒控制——线性矩阵不等式处理方法》俞立
【4】Iwasaki T,Hara S.Generalized KYP Lemma:unified frequency domain inequal-ities with design applications[J].IEEE Transactions on Automatic Control,2005,50(1):41–59.
【5】Wu J,Chen X,Gao H.H∞filtering with stochastic sampling[J].Signal Proces-siong,2010,90(4):1131–1145.
【6】Gao H,Wu J,Shi P.Robust sampled-data H∞control with stochastic sampling[J].Automatica,2009,45(7):1729–1736.
【7】Qiu J,Feng G,Yang J.New results on robust energy-to-peakfiltering for discrete-time switched polytopic linear systems with time-varying delay[J].IET ControlTheory and Applications,2008,2(9):795–806.
·
相关文章:
线性矩阵不等式(LMI)在控制理论中的应用
目录 (一)Matlab中的LMI处理工具包 (二)为什么LMI成为控制理论领域重要工具? (三)LMI在与Lyapunov不等式的关系 (1)线性矩阵不等式 (2)线性矩阵…...

如何在Python爬虫程序中使用HTTP代理?
在进行网络爬虫时,我们经常需要使用代理服务器来隐藏自己的真实IP地址,以避免被目标网站封禁或限制访问。本文将介绍如何将HTTP代理配置到Python爬虫程序中使用。 什么是HTTP代理? HTTP代理是一种网络代理,它充当客户端和服务器之…...

ARM架构指令集--专用指令
四、状态寄存器专用指令 CPSR寄存器-N Z C V T为0时 为ARM状态 F为0时 为开启FIQ状态 I为0时 为开启IRQ状态 图1 图2 一开始都是SVC指令,因为在操作系统启动的时候,在做一些初始化的操作,不允许被打断 图3 复位后CPSR寄存器为0xD3--…...

免费IP类api接口:含ip查询、ip应用场景查询、ip代理识别、IP行业查询...
免费IP类api接口:含ip查询、ip应用场景查询、ip代理识别… IP归属地-IPv6区县级:根据IP地址(IPv6版本)查询归属地信息,包含国家、省、市、区县和运营商等信息。IP归属地-IPv6城市级:根据IP地址(…...

Android Studio 中AGP ,Gradle ,JDK,SDK都是什么?
当进行 Android 开发时,以下是关键概念和工具的解释: Android Gradle Plugin: Android Gradle Plugin 是一个由 Google 提供的构建工具,它与 Gradle 配合使用来构建和打包 Android 应用。它提供了一组任务和功能,使开发…...
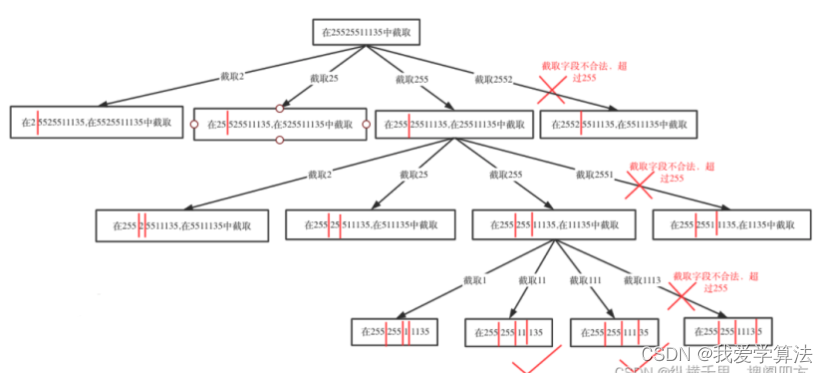
算法通关18关 | 回溯模板如何解决复原IP问题
18关的前几篇文章看过之后,对回溯的模板问题基本解题思路就知道了,就是固定的for循环问题,外层for循环控制横向,递归控制纵向,还要考虑撤销操作和元素是否能被重复利用问题,重复利用的情景较少,…...

Layui快速入门之第五节 导航
目录 一:基本概念 导航依赖element模块 API 渲染 属性 事件 二:水平导航 常规用法: 三:垂直导航 四:侧边垂直导航 五:导航主题 六:加入徽章等元素 七:面包屑导航 ps&a…...

使用分支——Git Checkout
这篇文章写的挺好; https://zhuanlan.zhihu.com/p/465954849 这里要注意,git 新的命令,通过 git switch 切换分支,虽然git checkout 分支 还可以用; 游离状态的HEADS 在我们已经见识到git checkout命令对于分支的三…...
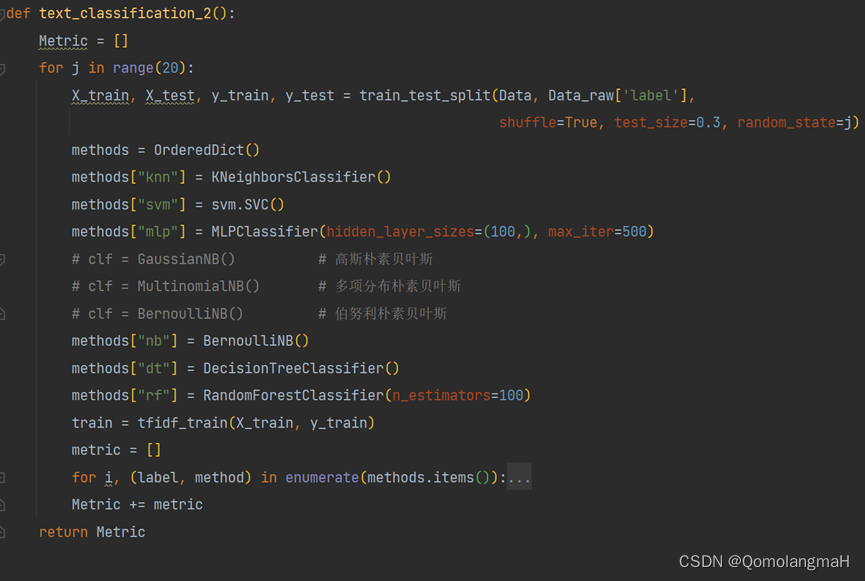
【2023】数据挖掘课程设计:基于TF-IDF的文本分类
目录 一、课程设计题目 基于TF-IDF的文本分类 二、课程设计设置 1. 操作系统 2. IDE 3. python 4. 相关的库 三、课程设计目标 1. 掌握数据预处理的方法,对训练集数据进行预处理; 2. 掌握文本分类建模的方法,对语料库的文档进行建模…...
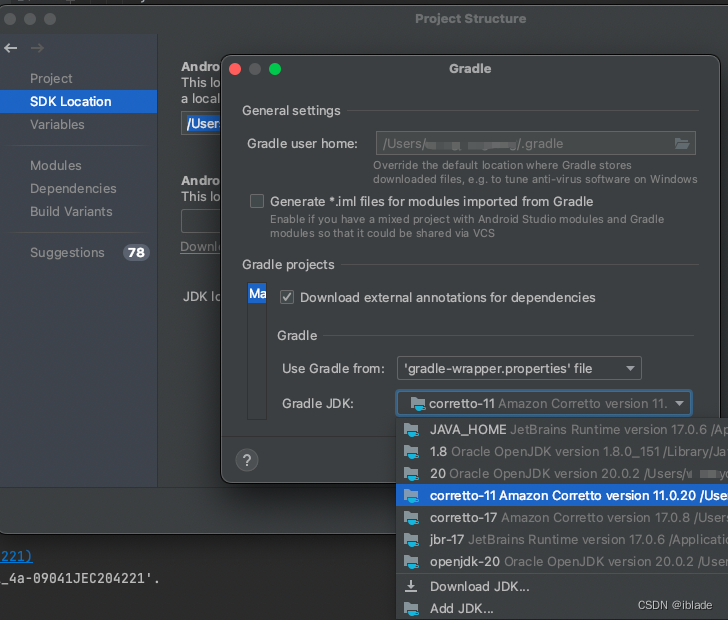
java.lang.NoSuchMethodError: java.lang.reflect.Field.trySetAccessible()Z
java.lang.NoSuchMethodError: java.lang.reflect.Field.trySetAccessible()Z 将JDK升级为11即可。 File --Project Structure – SDK Location --Gradle Setting --Gradle JDK 选择11...

如何使用SQL系列 之 如何在MySQL中使用存储过程
引言 通常,当使用关系型数据库时,你直接在应用程序代码中发出单独的结构化查询语言(SQL)查询来检索或操作数据,如SELECT、INSERT、UPDATE或DELETE。这些语句直接作用于并操作底层数据库表。如果相同的语句或一组语句中使用多个应用程序访问同…...

用 Github Codespaces 免费搭建本地开发测试环境
如何丝滑地白嫖一个本地开发环境?怎么新建一个代码空间? 1:通过Github网页新建2:通过VSCode插件新建 为代码创建相应的开发测试环境 如何丝滑地白嫖一个本地开发环境? 使用Codespaces为开发者解决这样的痛点…...
PyTorch实战-实现神经网络图像分类基础Tensor最全操作详解(一)
目录 前言 一、PyTorch数据结构-Tensor 1.什么是Tensor 2.数据Tensor使用场景 3.张量形态 标量(0D 张量) 向量(1D 张量) 矩阵(2D张量) 3D 张量与高维张量 二、Tensor的创建 1. 从列表或NumPy数组创建 2. 使用特定的初始…...
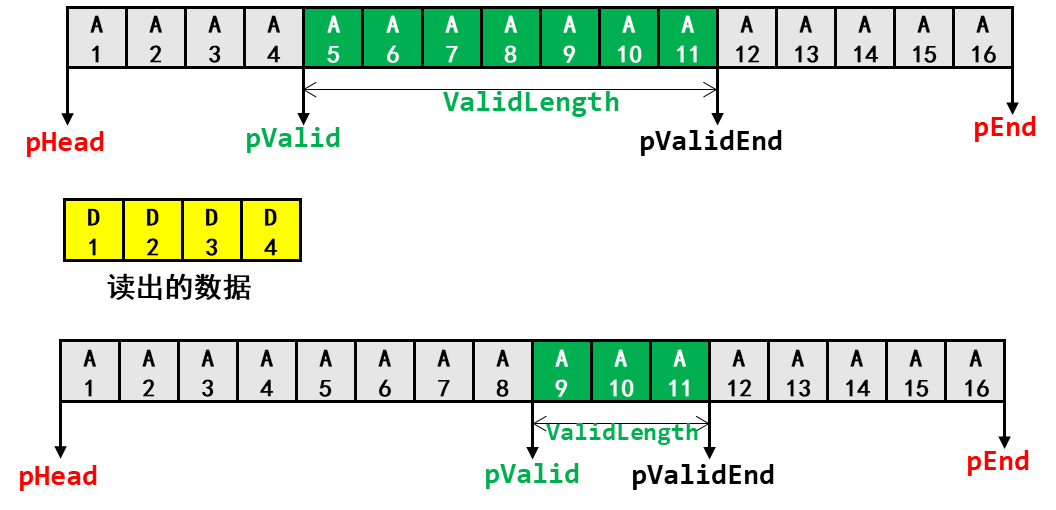
第29章_瑞萨MCU零基础入门系列教程之改进型环形缓冲区
本教程基于韦东山百问网出的 DShanMCU-RA6M5开发板 进行编写,需要的同学可以在这里获取: https://item.taobao.com/item.htm?id728461040949 配套资料获取:https://renesas-docs.100ask.net 瑞萨MCU零基础入门系列教程汇总: ht…...
)
如何搭建一个react项目(详细介绍)
要搭建一个基本的 React 项目,你需要执行以下步骤。在开始之前,请确保你已经安装了 Node.js 和 npm(Node 包管理器)。 搭建一个React项目 1,创建项目目录2,初始化项目3,安装 React 和 ReactDOM4…...

ActiveMQ用法
ActiveMQ 和 JMS的关系? ActiveMQ是流行的开源消息中间件,JMS是Java平台定义的一种消息传递的标准。ActiveMQ实现了JMS规范,因此可以使用JMS API来与ActiveMQ进行交互。 JMS定义了一种标准的API。API包括了一些接口和类,用于创建…...
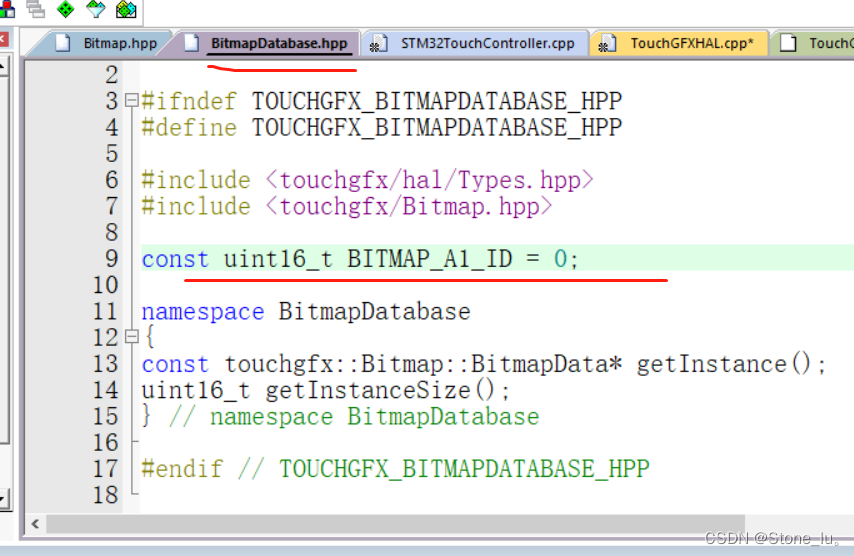
TouchGFX之缓存位图
位图缓存是专用RAM缓冲区,应用可将位图保存(或缓存)在其中。 如果缓存了位图,在绘制位图时,TouchGFX将自动使用RAM缓存作为像素来源。位图缓存在许多情况下十分有用。 从RAM读取数据通常比从闪存读取要快(特…...
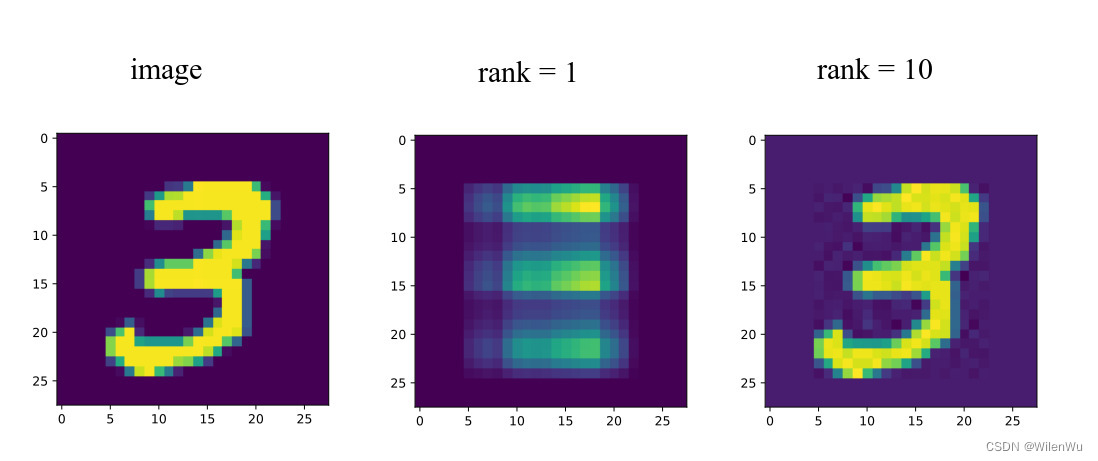
线性代数的本质(十)——矩阵分解
文章目录 矩阵分解LU分解QR分解特征值分解奇异值分解奇异值分解矩阵的基本子空间奇异值分解的性质矩阵的外积展开式 矩阵分解 矩阵的因式分解是把矩阵表示为多个矩阵的乘积,这种结构更便于理解和计算。 LU分解 设 A A A 是 m n m\times n mn 矩阵,…...

vue实现鼠标拖拽div左右移动的功能
直接代码: <template><div class"demo"><div class"third-part" id"发展历程"><div class"title">发展历程</div><div class"content" id"nav" v-if"dataList…...
基于Python和mysql开发的商城购物管理系统分为前后端(源码+数据库+程序配置说明书+程序使用说明书)
一、项目简介 本项目是一套基于Python和mysql开发的商城购物管理系统,主要针对计算机相关专业的正在做毕设的学生与需要项目实战练习的Python学习者。 包含:项目源码、项目文档、数据库脚本等,该项目附带全部源码可作为毕设使用。 项目都经过…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...

Python环境安装与虚拟环境配置详解
本文档旨在为Python开发者提供一站式的环境安装与虚拟环境配置指南,适用于Windows、macOS和Linux系统。无论你是初学者还是有经验的开发者,都能在此找到适合自己的环境搭建方法和常见问题的解决方案。 快速开始 一分钟快速安装与虚拟环境配置 # macOS/…...