定积分的计算:牛顿-莱布尼茨公式
目录
牛顿-莱布尼茨公式
用C语言代码实现
利用换元积分法和分部积分法
利用奇偶性和周期性求积分
利用已有公式求积分

牛顿-莱布尼茨公式
牛顿-莱布尼茨公式(Newton-Leibniz formula)是微积分学中的基本定理之一,它反映了定积分与被积函数的原函数或者不定积分之间的联系。具体来说,它表明了一个连续函数f(x)在区间[a,b]上的定积分等于它的任意一个原函数F(x)在区间[a,b]上的增量F(b)-F(a)。这个公式最早是由牛顿在1666年提出的,后来在1713年莱布尼茨在一篇手稿中也独立发现。
牛顿-莱布尼茨公式的现代形式可以简单地表述为∫f(x)dx=F(b)-F(a),其中F(x)是f(x)的一个原函数。这个公式给定积分提供了一个有效而简便的计算方法,大大简化了定积分的计算过程。
推导过程可以简单地描述为:任取区间[a,b]上的分割,记分点为ξi,则有f(ξi)Δxi,其中Δxi表示第i个小区间的宽度。对所有的Δxi应用拉格朗日中值定理得到f'(ξi)=f(b)-f(a),然后对所有的f'(ξi)求和得到F'(b)-F'(a)=f(b)-f(a),最后两边同时积分得到∫f(x)dx=F(b)-F(a)。
在实际计算中,可以根据被积函数的解析式来选择合适的原函数,从而简化计算。比如对于f(x)=x^2,它的不定积分是F(x)=x^3/3,那么在区间[1,3]上计算定积分∫x^2 dx 就可以直接计算F(3)-F(1)得到结果。
总之,牛顿-莱布尼茨公式是微积分学中的一个重要定理,它提供了一种简便的计算定积分的方法,同时也揭示了定积分与不定积分之间的联系。
用C语言代码实现
牛顿-莱布尼茨公式(Newton-Leibniz formula)是微积分学中的基本定理之一,它反映了定积分与被积函数的原函数或者不定积分之间的联系。具体来说,它表明了一个连续函数f(x)在区间[a,b]上的定积分等于它的任意一个原函数F(x)在区间[a,b]上的增量F(b)-F(a)。这个公式最早是由牛顿在1666年提出的,后来在1713年莱布尼茨在一篇手稿中也独立发现。
以下是使用C语言实现牛顿-莱布尼茨公式的示例代码:
#include <stdio.h> // 定义被积函数f(x) double f(double x) { return x * x + 1; } // 定义f(x)的原函数F(x) double F(double x) { return x * x * x / 3 + x; } // 使用牛顿-莱布尼茨公式计算定积分 double integral(double a, double b) { return F(b) - F(a); } int main() { double a = 0; // 积分下限 double b = 1; // 积分上限 double result = integral(a, b); // 计算定积分 printf("The integral of f(x) from %f to %f is %f\n", a, b, result); return 0; }在这个示例中,我们定义了被积函数f(x)=x^2+1,它的原函数F(x)=x^3/3+x。然后,我们使用牛顿-莱布尼茨公式计算f(x)在区间[0,1]上的定积分,即F(1)-F(0)。最后,我们输出计算结果。
利用换元积分法和分部积分法
我们可以利用换元积分法和分部积分法来求解定积分。
首先,对于换元积分法,我们可以将原来的积分变量换成一个新的变量,使得积分变得更加简单。
例如,对于积分 ∫(0到1) (x^2+1) dx,我们可以令x=√t,则dx=dt/(2√t),于是原积分变为:
∫(0到1) (x^2+1) dx = ∫(0到1) ((√t)^2+1) dt/(2√t)
= 1/(2√t) ∫(0到1) (t+1) dt
= 1/(2√t) (t^2/2+t) |(0到1)
= 1/(2√1) (1^2/2+1) - 1/(2√0) (0^2/2+0)
= 3/(4√1) - 0
= 3/(4√1)
= 3/(4)
接下来,对于分部积分法,我们可以将原来的积分拆成两个函数的乘积,然后分别求导和积分,使得积分变得更加简单。
例如,对于积分 ∫(0到1) xlnx dx,我们可以令u=lnx,则du=dx/x,于是原积分变为:
∫(0到1) xlnx dx = ∫(0到1) xudu
= xu - ∫(0到1) udx
= xu - ∫(0到1) lnx dx
= xu - xlnx + ∫(0到1) dx
= xu - xlnx + x |(0到1)
= (1)(ln1-0)+(1-0)(1-0)
= 1
利用奇偶性和周期性求积分
首先,我们需要知道奇偶性和周期性的定义:
奇函数:f(-x) = -f(x)
偶函数:f(-x) = f(x)
周期函数:f(x+T) = f(x)
对于奇函数,如果积分区间对称,那么积分值为0。
对于偶函数,如果积分区间对称,那么可以将积分区间缩小一半。
对于周期函数,如果积分区间是周期的整数倍,那么可以将积分区间缩小一个周期。
现在,我们来求解这个积分:
∫(-2到2) (x^3 - 2x^2 + 3) dx
首先,我们可以将积分区间缩小一半:
∫(-2到2) (x^3 - 2x^2 + 3) dx = 2 ∫(0到2) (x^3 - 2x^2 + 3) dx
然后,我们可以利用周期性将积分区间缩小一个周期:
∫(0到2) (x^3 - 2x^2 + 3) dx = ∫(0到1) (x^3 - 2x^2 + 3) dx + ∫(1到2) (x^3 - 2x^2 + 3) dx
∫(1到2) (x^3 - 2x^2 + 3) dx = ∫(0到1) ((x+1)^3 - 2(x+1)^2 + 3) dx
接下来,我们可以将奇函数的积分值为0的性质应用到第一个积分中:
∫(0到1) (x^3 - 2x^2 + 3) dx = ∫(0到1) (x^3 - 2x^2) dx + ∫(0到1) 3 dx
∫(0到1) (x^3 - 2x^2) dx = 0
最后,我们将所有的结果代入原式:
∫(-2到2) (x^3 - 2x^2 + 3) dx = 6
利用已有公式求积分
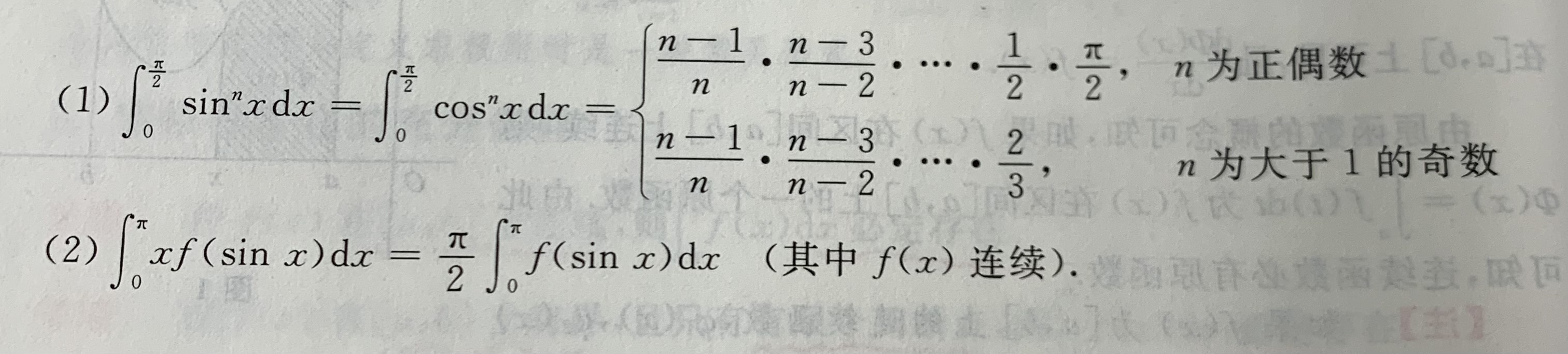
相关文章:
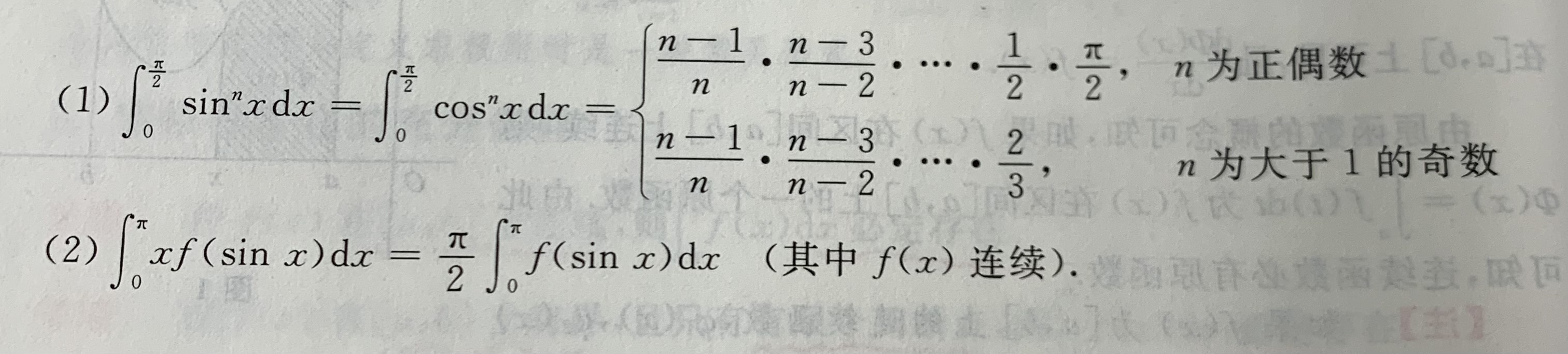
定积分的计算:牛顿-莱布尼茨公式
目录 牛顿-莱布尼茨公式 用C语言代码实现 利用换元积分法和分部积分法 利用奇偶性和周期性求积分 利用已有公式求积分 牛顿-莱布尼茨公式 牛顿-莱布尼茨公式(Newton-Leibniz formula)是微积分学中的基本定理之一,它反映了定积分与被积函…...

shell脚本之case 的用法
shell脚本之case case是Shell脚本中的一种控制流语句,它允许根据变量的值选择不同的执行路径。case语句的语法如下: case word in pattern [| pattern]...) command-list ;; pattern [| pattern]...) command-list ;; ... *) command-list ;; esa…...
)
第3章 helloworld 驱动实验(iTOP-RK3568开发板驱动开发指南 )
在学习C语言或者其他语言的时候,我们通常是打印一句“helloworld”来开启编程世界的大门。学习驱动程序编程亦可以如此,使用helloworld作为我们的第一个驱动程序。 接下来开始编写第一个驱动程序—helloworld。 3.1 驱动编写 本小节来编写一个最简单的…...
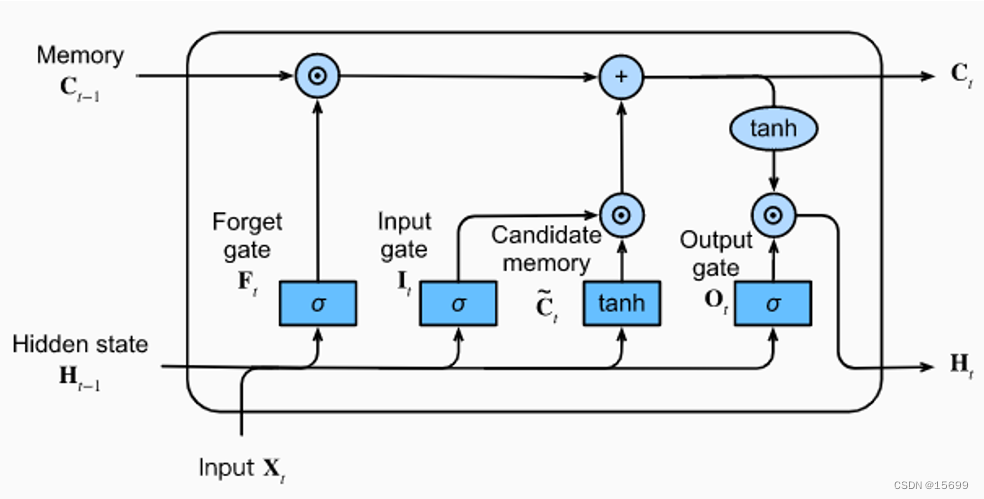
基于PyTorch使用LSTM实现新闻文本分类任务
本文参考 PyTorch深度学习项目实战100例 https://weibaohang.blog.csdn.net/article/details/127154284?spm1001.2014.3001.5501 文章目录 本文参考任务介绍做数据的导入 环境介绍导入必要的包介绍torchnet和keras做数据的导入给必要的参数命名加载文本数据数据前处理模型训…...

Flutter插件的制作和发布
Flutter制作插件有两种方式(以下以android和ios为例): 目录 1.直接在主工程下的android和ios项目内写插件代码:2.创建独立Flutter Plugin项目,制作各端插件后,再引入项目:1. 创建Flutter Plugin…...
【JAVA】异常
作者主页:paper jie 的博客 本文作者:大家好,我是paper jie,感谢你阅读本文,欢迎一建三连哦。 本文录入于《JAVASE语法系列》专栏,本专栏是针对于大学生,编程小白精心打造的。笔者用重金(时间和…...

合同矩阵充要条件
两个实对称矩阵合同的充要条件是它们的正负惯性指数相同。 正惯性指数是矩阵正特征值个数,负惯性指数是矩阵负特征值个数。 即合同矩阵的充分必要条件是特征值的正负号个数相同。 证明: 本论证中的所有矩阵都是对称矩阵。 根据定义,若矩…...
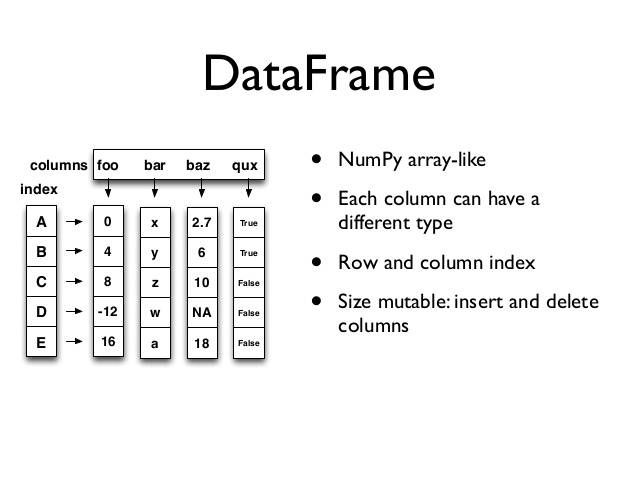
数据分析三剑客之Pandas
1.引入 前面一篇文章我们介绍了numpy,但numpy的特长并不是在于数据处理,而是在它能非常方便地实现科学计算,所以我们日常对数据进行处理时用的numpy情况并不是很多,我们需要处理的数据一般都是带有列标签和index索引的࿰…...

Spring Boot自动装配原理
简介 Spring Boot是一个开源的Java框架,旨在简化Spring应用程序的搭建和开发。它通过自动装配的机制,大大减少了繁琐的配置工作,提高了开发效率。本文将深入探讨Spring Boot的自动装配原理。 自动装配的概述 在传统的Spring框架中…...

VMware Workstation虚拟机网络配置及配置自动启动
目录 一、网络配置二、配置自动启动1.VMware 中配置虚拟机自启动2.系统服务中配置 VMware 服务自启动 一、网络配置 本文将虚拟机 IP 与主机 IP 设置为同一个网段。 点击 “编辑” -> “虚拟网络编辑器(N)…”: 点击 “更改设置”: 将 VMnet0 设置…...

智能语音机器人竞品调研
一、腾讯云-智能客服机器人 链接地址:智能客服机器人_在线智能客服_智能客服解决方案 - 腾讯云 二、阿里云-智能语音机器人 链接地址:智能对话机器人-阿里云帮助中心 链接地址:智能外呼机器人的业务架构_智能外呼机器人-阿里云帮助中心 三、火…...
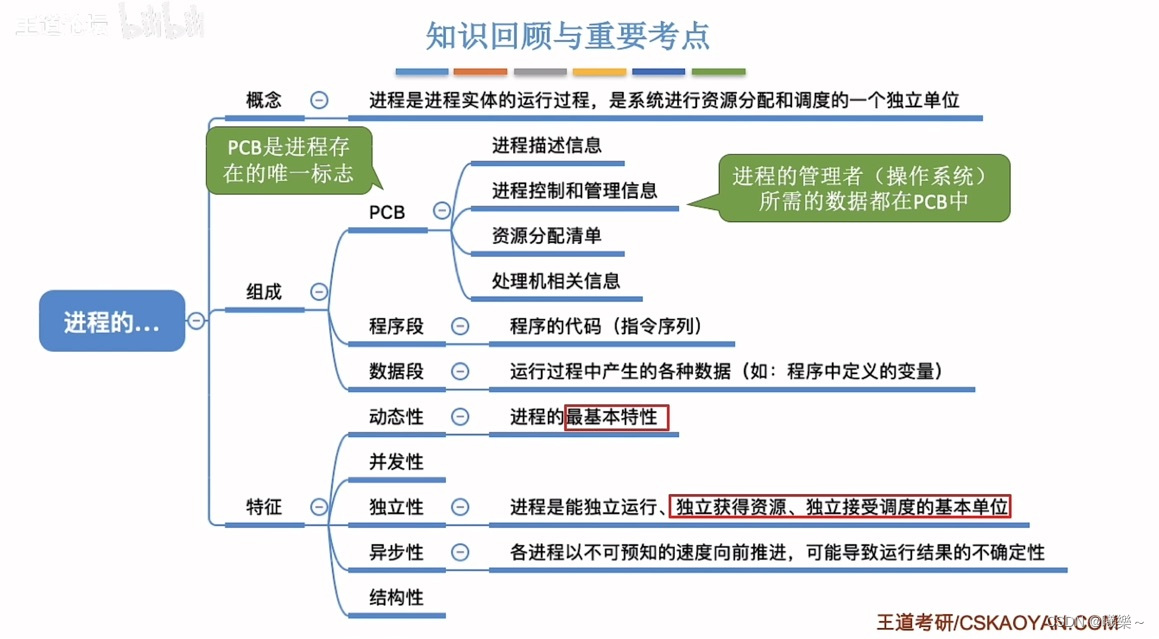
【操作系统】进程的概念、组成、特征
概念组成 程序:静态的放在磁盘(外存)里的可执行文件(代码) 作业:代码+数据+申请(JCB)(外存) 进程:程序的一次执行过程。 …...

大二第二周总结
问题: 想到了之前追的辩论赛,主题是“被误解是表达者的宿命”, 反方认为被误解不是表达者的宿命: 由于表达者表意含混造成误解的可能性是人力可控的,表达者可在真诚沟通的基础之上,根据对方反应不断调整…...

JDK、eclipse软件的安装
一、打开JDK安装包 二、复制路径 三、点击我的电脑,找到环境变量 四、新建环境 变量名:JAVA_HOME 变量值就是刚刚复制的路径 五、在path中建立新变量 双击path 打印以下文字 最后一直双击确定,安装环境完成。 六、双击eclipse 选择好安装…...

235. 二叉搜索树的最近公共祖先 Python
文章目录 一、题目描述示例 1示例 2 二、代码三、解题思路 一、题目描述 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足…...
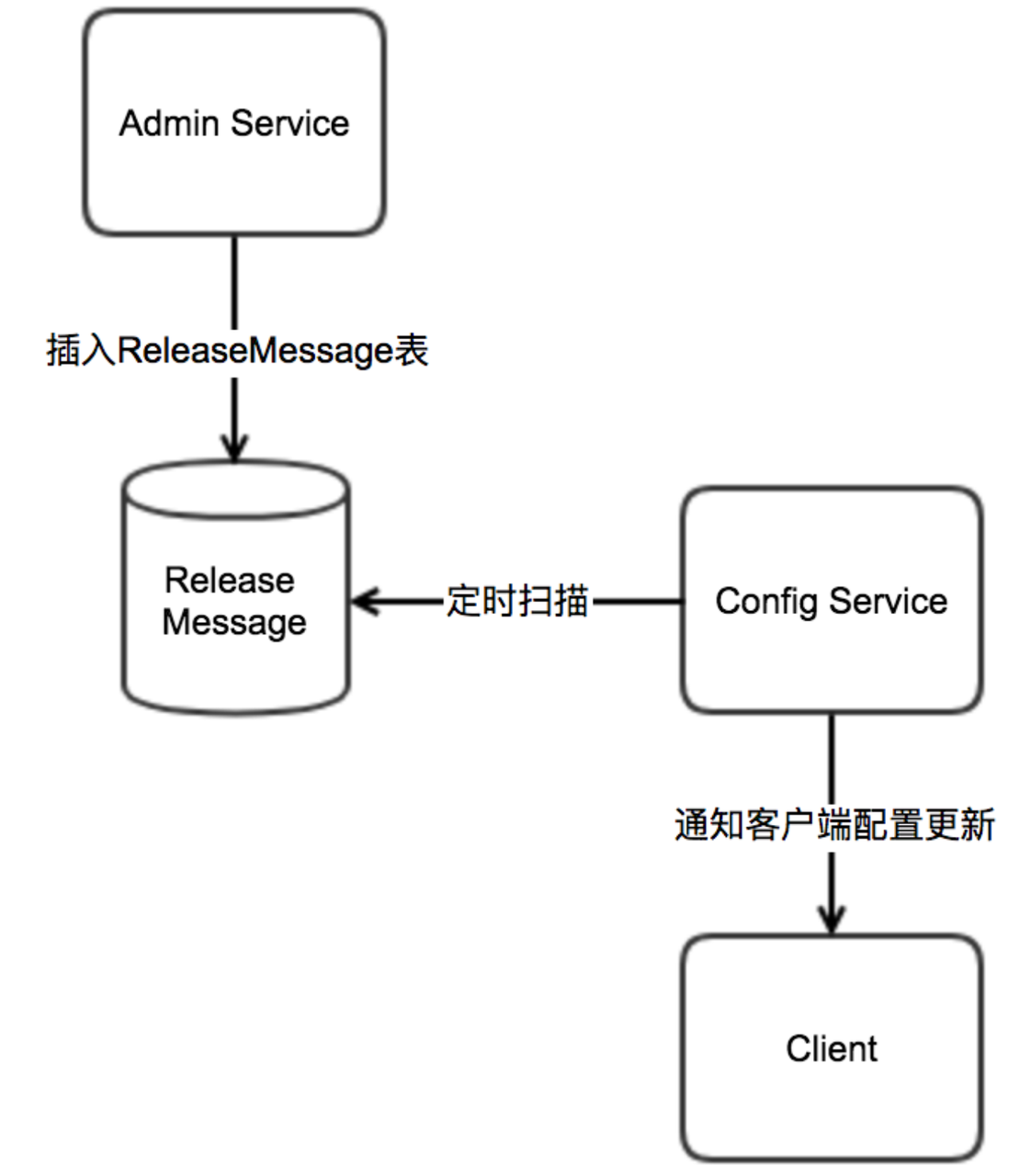
Apollo介绍和入门
文章目录 Apollo介绍配置中心介绍apollo介绍主流配置中心功能特性对比 Apollo简介 入门简单的执行流程Apollo具体的执行流程Apollo对象执行流程分步执行流程 核心概念应用,环境,集群,命名空间企业部署方案灰度发布全量发布 配置发布的原理发送…...
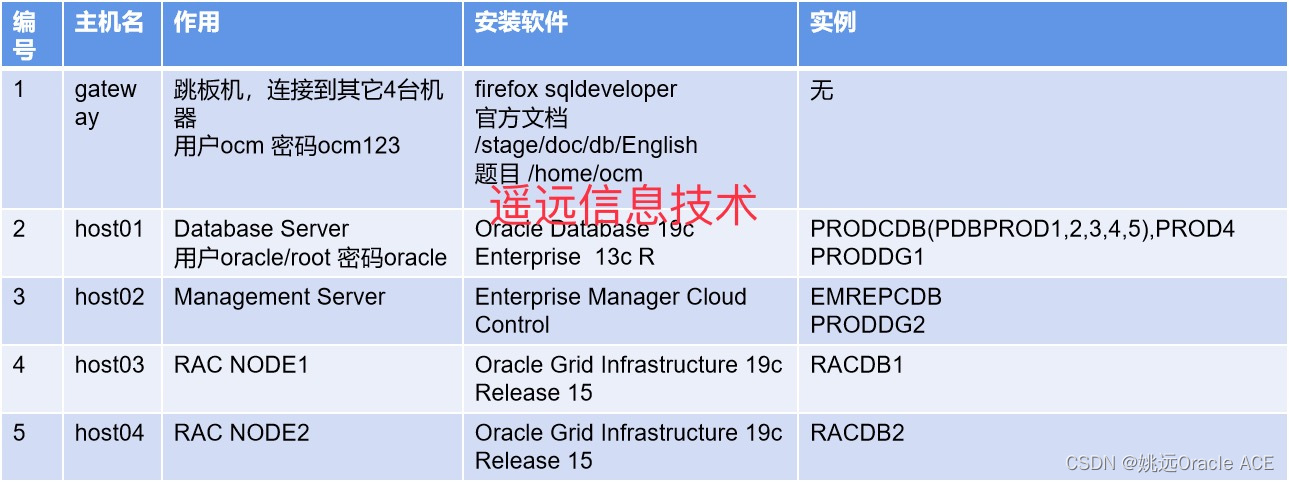
一文看懂Oracle 19c OCM认证考试(需要Oracle OCP证书)
Oracle OCM的认证全称是Oracle Certified Master,是比OCP更高一级的认证,姚远老师的很多OCP学员都对OCM考试有兴趣,这里跟大家做个介绍。 OCM考试全部是上机的实操考试,没有笔试,要到Oracle原厂参加两天的考试。参加1…...
回归预测 | MATLAB实现PSO-SDAE粒子群优化堆叠去噪自编码器多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现PSO-SDAE粒子群优化堆叠去噪自编码器多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现PSO-SDAE粒子群优化堆叠去噪自编码器多输入单输出回归预测(多指标,多图)效果一览…...
python自学
自学第一步 第一个简单的基础,向世界说你好 启动python 开始 print是打印输出的意思,就是输出引号内的内容。 标点符号必须要是英文的,因为他只认识英文的标点符号。 exit()推出python。 我们创建一个文本文档&…...
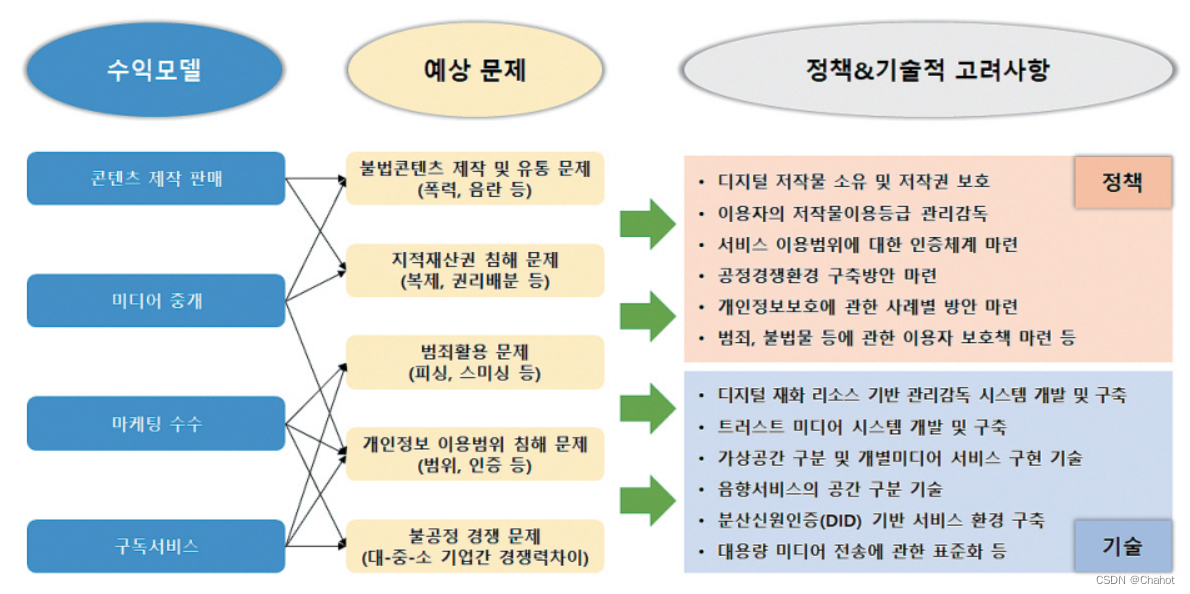
元宇宙安全与著作权相关市场与技术动态:韩国视角
元宇宙市场动态 元宇宙安全与著作权维护技术现状 元宇宙有可能为商业创造巨大价值,尤其是在零售和时尚领域。时尚产品的象征性价值不仅在物理空间中得以保持,在虚拟空间中也是如此。通过元宇宙平台,企业可以开发虚拟产品,降低供…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...
