线段树上树剖再拿线段树维护:0914T4
cp
一种常见套路:
如果在线段树上进行一段区间修改,那么必然是一段右节点+一段左节点
这个过程其实就是zkw的本质
下面都要用zkw来理解
考虑原题,有一棵不规则的线段树
类似zkw,在这类题目中,我们要先把开区间变成闭区间
然后每个点记录其兄弟节点的信息
考虑现在区间为 ( x , y ) (x,y) (x,y),我们可以先求出其 z = l c a ( x , y ) z=lca(x,y) z=lca(x,y)
则 x x x 要跳到 l s [ z ] ls[z] ls[z], y y y 要跳到 r s [ z ] rs[z] rs[z]
x x x 在跳的过程中,如果它是左节点那么就修改/统计它的右节点
我们可以回顾zkw的过程帮助理解:

然后现在考虑优化跳的这个过程。
我们发现这就是个树剖。
然后就完成啦
时间复杂度 O ( n log 2 n ) O(n\log^2n) O(nlog2n)
线段树套线段树
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back#define N 400010
int n, m, i, j, k, T;
int f[N][22], q, x, y, ans, dep[N], lxy, op, d, mp[N]; struct Segment_tree {int tot, ls[N<<1], rs[N<<1], rt; int s[N<<1], tag[N<<1], len[N<<1]; void build(int &k, int l, int r) {if(!k) k=++tot; if(l==r) return ; int mid=(l+r)>>1; build(ls[k], l, mid); build(rs[k], mid+1, r); }void make(int k, int l, int r, int x, int y) {if(l==r) return len[k]=y, void(); int mid=(l+r)>>1; if(x<=mid) make(ls[k], l, mid, x, y); else make(rs[k], mid+1, r, x, y); len[k]=len[ls[k]]+len[rs[k]]; }void add(int k, int l, int r, int x, int y, int z) {if(l>=x && r<=y) {tag[k]+=z; s[k]+=len[k]*z; return ; }tag[ls[k]]+=tag[k]; s[ls[k]]+=len[ls[k]]*tag[k]; tag[rs[k]]+=tag[k]; s[rs[k]]+=len[rs[k]]*tag[k]; tag[k]=0; int mid=(l+r)>>1; if(x<=mid) add(ls[k], l, mid, x, y, z); if(y>=mid+1) add(rs[k], mid+1, r, x, y, z); s[k]=s[ls[k]]+s[rs[k]]; }int que(int k, int l, int r, int x, int y) {if(l>=x && r<=y) return s[k]; int mid=(l+r)>>1, sum=0; tag[ls[k]]+=tag[k]; s[ls[k]]+=len[ls[k]]*tag[k]; tag[rs[k]]+=tag[k]; s[rs[k]]+=len[rs[k]]*tag[k]; tag[k]=0; if(x<=mid) sum+=que(ls[k], l, mid, x, y); if(y>=mid+1) sum+=que(rs[k], mid+1, r, x, y); return sum; }
}S1, S2;struct Tree_chain_pou_score {int ls[N], rs[N], tot; int w[N], st[N], ed[N], len[N]; int up[N], dfn[N], p[N]; int son[N], ltson[N]; void dfs1(int x) {if(x<=n) {st[x]=ed[x]=x; w[x]=1; return ; }f[ls[x]][0]=f[rs[x]][0]=x; dep[ls[x]]=dep[rs[x]]=dep[x]+1; dfs1(ls[x]); dfs1(rs[x]); st[x]=st[ls[x]]; ed[x]=ed[rs[x]]; w[x]=w[ls[x]]+w[rs[x]]+1; }void dfs2(int x, int Up) {up[x]=Up; dfn[x]=++tot; p[x]=tot; len[x]=ed[x]-st[x]+1; if(x<=n) return ; if(w[ls[x]]>w[rs[x]]) son[x]=ls[x], ltson[x]=rs[x]; else son[x]=rs[x], ltson[x]=ls[x]; dfs2(son[x], Up); dfs2(ltson[x], ltson[x]); S1.make(1, 1, m, dfn[ls[x]], len[rs[x]]); S2.make(1, 1, m, dfn[rs[x]], len[ls[x]]); }void add(Segment_tree &Seg, int x, int y, int z) {while(up[x]!=up[y]) {Seg.add(1, 1, m, dfn[up[x]], dfn[x], z); x=f[up[x]][0]; }if(x==y) return ; Seg.add(1, 1, m, dfn[y]+1, dfn[x], z); }int que(Segment_tree &Seg, int x, int y) {int ans=0; while(up[x]!=up[y]) {ans+=Seg.que(1, 1, m, dfn[up[x]], dfn[x]); x=f[up[x]][0]; }if(x==y) return ans; ans+=Seg.que(1, 1, m, dfn[y]+1, dfn[x]); return ans; }
}Tree;int lca(int x, int y) {if(x==y) return x; if(dep[x]<dep[y]) swap(x, y); for(int k=20; k>=0; --k)if(dep[f[x][k]]>=dep[y]) x=f[x][k]; if(x==y) return x; for(int k=20; k>=0; --k)if(f[x][k]!=f[y][k]) x=f[x][k], y=f[y][k]; return f[x][0];
}signed main()
{freopen("pigeons.in", "r", stdin);freopen("pigeons.out", "w", stdout);n=read(); q=read(); for(i=n+1; i<2*n; ++i) {Tree.ls[i+2]=read(); Tree.rs[i+2]=read(); if(Tree.ls[i+2]<=n) Tree.ls[i+2]++; else Tree.ls[i+2]+=2; if(Tree.rs[i+2]<=n) Tree.rs[i+2]++; else Tree.rs[i+2]+=2; mp[Tree.ls[i+2]]=mp[Tree.rs[i+2]]=1; }for(i=n+3; mp[i]; ++i); Tree.ls[2*n+2]=1; Tree.rs[2*n+2]=i; Tree.ls[2*n+3]=2*n+2; Tree.rs[2*n+3]=n+2; m=2*n+3; n=n+2; dep[m]=1; Tree.dfs1(m); S1.build(S1.rt, 1, m); S2.build(S2.rt, 1, m); Tree.dfs2(m, m); for(k=1; k<=20; ++k)for(i=1; i<=m; ++i) {f[i][k]=f[f[i][k-1]][k-1]; }while(q--) {op=read(); if(op==1) {x=read()+1; y=read()+1; d=read(); lxy=lca(x-1, y+1); Tree.add(S1, x-1, Tree.ls[lxy], d); Tree.add(S2, y+1, Tree.rs[lxy], d); }else {x=read()+1; y=read()+1; lxy=lca(x-1, y+1); ans=0; ans+=Tree.que(S1, x-1, Tree.ls[lxy]); ans+=Tree.que(S2, y+1, Tree.rs[lxy]); printf("%lld\n", ans); }}return 0;
}相关文章:

线段树上树剖再拿线段树维护:0914T4
cp 一种常见套路: 如果在线段树上进行一段区间修改,那么必然是一段右节点一段左节点 这个过程其实就是zkw的本质 下面都要用zkw来理解 考虑原题,有一棵不规则的线段树 类似zkw,在这类题目中,我们要先把开区间变成闭…...
互联网医院系统|互联网医院探索未来医疗的新蓝海
随着互联网技术的飞速发展,互联网医院应运而生,为人们带来全新的医疗体验。本文将深入探讨互联网医院的开发流程、系统优势以及未来发展方向,带您领略医疗领域的新蓝海。互联网医院的开发流程是一个结合技术、医疗和用户需求的复杂过程。首先…...

Acrel-2000系列监控系统在亚运手球比赛馆建设10kV供配电工程中的应用
安科瑞 崔丽洁 摘要:智能化配电监控系统是数字化和信息化时代应运而生的产物,已经被广泛应用于电网用户侧楼宇、体育场馆、科研设施、机场、交通、医院、电力和石化行业等诸多领域的高/低压变配电系统中。安科瑞自研的Acrel-2000系列监控系统可监控高压开关柜、低压…...

c++中遇到一个不了解的函数,查看能用的接口功能
在C中,您可以使用几种方法来查找函数的接口和使用方式。下面是一些常用的方法: 查阅官方文档:每个常见的C库都应该配有官方文档,其中包含所有可用函数和其接口的详细说明。您可以从官方网站或下载的文档中查找所需函数的接口和使用…...
windows linux子系统 docker无法启动
windows安装Linux子系统后,使用sudo service docker start启动后,再使用sudo service docker status查看docker状态,docker无法启动,使用sudo dockerd查看错误信息如下: failed to start daemon: Error initializing …...

【Redis】深入探索 Redis 的数据类型 —— 无序集合 Set
文章目录 一、Set 类型介绍二、Set 类型相关命令2.1 添加元素和检查成员2.2 移除元素2.3 集合运算求交集求并集求差集 2.4 Set 相关命令总结 三、Set 类型编码方式四、Set 使用场景 一、Set 类型介绍 Set(集合)是 Redis 数据库中的一种数据类型…...

可变参数JAVA
public class Main {public static void main(String[] args) {//方法形参的个数是可以变化的//格式:属性类型...名字System.out.println(getSum(1,2,3,4,5,6,7,8));}//通过键值对对象来遍历;public static int getSum(int a,int...args){//可变参数;int…...
Zabbix监控平台部署流程
Zabbix WEB、Zabbix Server、Zabbix Database放在一台服务器;(192.168.10.12)Zabbix Agent部署在被监控服务器上 (192.168.10.11)Zabbix Porxy 单独部署在一台服务器上(被监控服务器少于500台可以不部署&am…...

重磅!文晔以38亿美元收购富昌电子 | 百能云芯
文晔微电子股份有限公司(文晔科技)于9月14日正式宣布已完成对富昌电子公司(Future Electronics Inc.)100%股权的收购,该交易以全现金方式完成,总交易价值高达38亿美元。 文晔科技的董事长兼首席执行官郑家强…...

Multimodel Image synthesis and editing:The generative AI Era
1.introduction 基于GAN和扩散模型,通过融入多模态引导来调节生成过程,从不同的多模态信号中合成图像;是为多模态图像合成和编辑使用预训练模型,通过在GAN潜在空间中进行反演,应用引导函数,或调整扩散模型…...
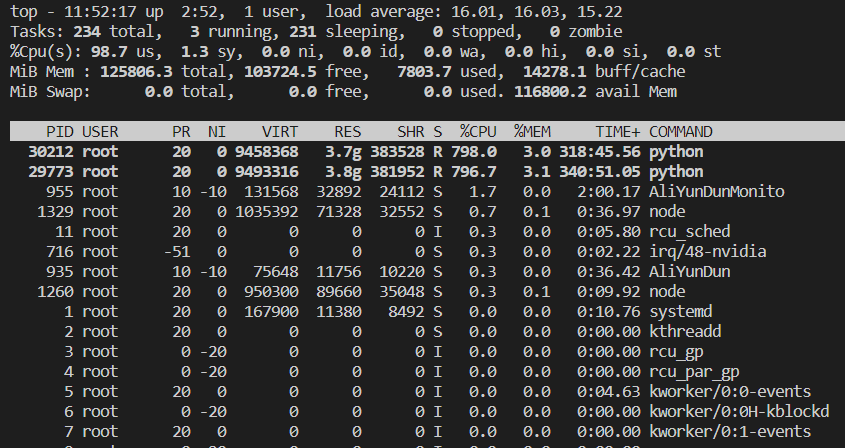
Linux——(第十章)进程管理
目录 一、概述 二、常用指令 1.ps查看当前系统进程状态 2.kill 终止进程 3.pstree 查看进程树 4.top 实时监控系统进程状态 5.netstat 监控网络状态 一、概述 (1)进程是正在执行的一个程序或命令,每一个进程都是一个运行的实体&#…...
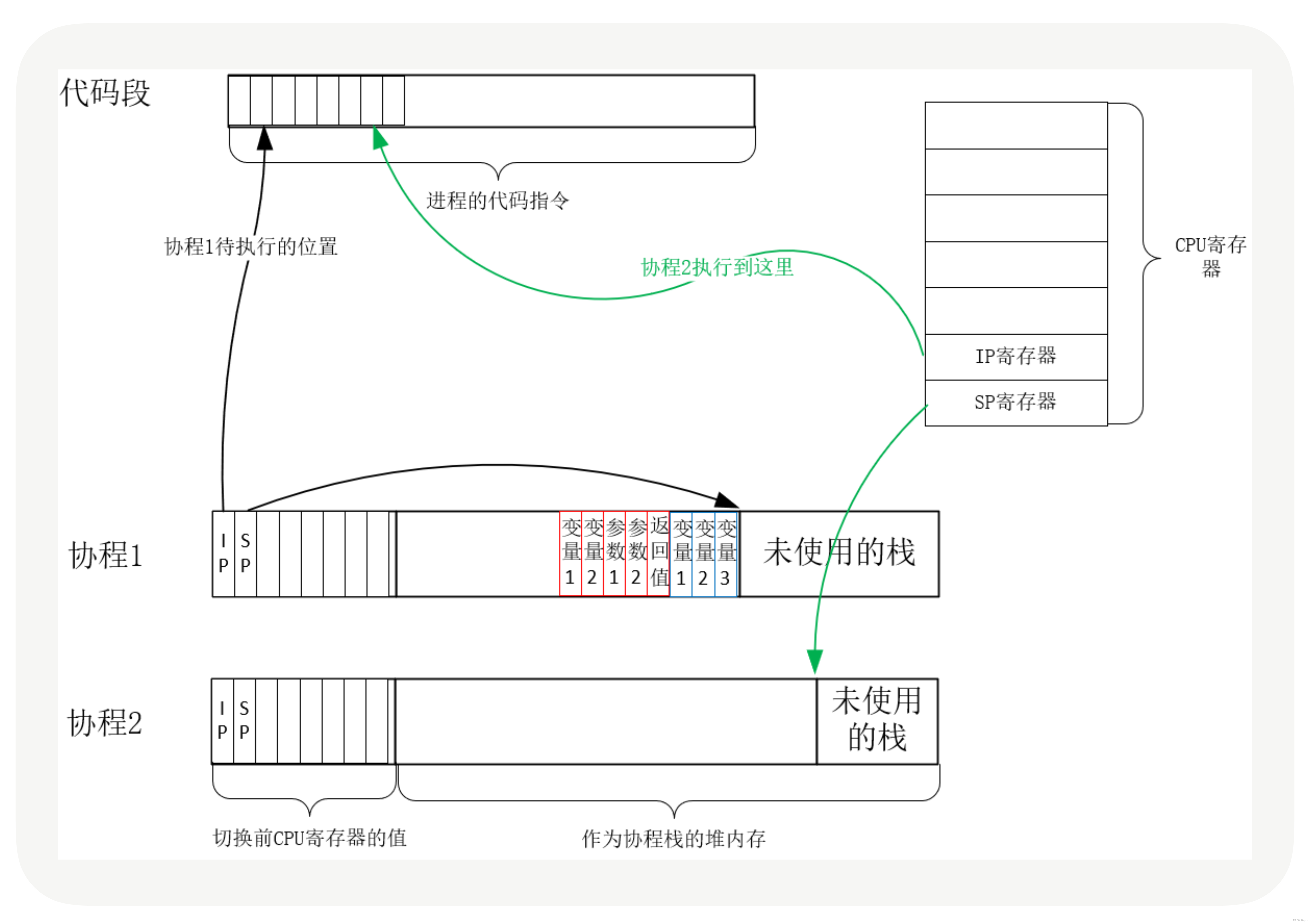
【操作系统】聊聊协程为什么可以支撑高并发服务
在实际的业务开发中,比如针对一个业务流程,调用三方,然后存储数据,从oss上获取数据。其实都是进行的同步调用,说白了就是A完成之后,B在继续完成。如果整个过程中A、B、C 分别耗时100、300、200毫秒。那么整…...
)
算法leetcode|80. 删除有序数组中的重复项 II(rust重拳出击)
文章目录 80. 删除有序数组中的重复项 II:样例 1:样例 2:提示: 分析:题解:rust:go:c:python:java: 80. 删除有序数组中的重复项 II: …...

Vite 完整版详解
1. 打包构建: Vite 使用 Rollup 作为默认的构建工具。通过运行 npm run build 命令,Vite 会将应用程序的源代码打包成一个或多个优化的静态文件,以便在生产环境中进行部署。Vite 的构建过程会根据需要进行代码拆分、压缩和优化,以…...

AI入门指南:探索人工智能的基础原理和实际应用
引言 介绍AI的基本概念:什么是人工智能,为什么它如此重要。 引出博客的主要内容,即AI的基础原理和实际应用。 第一部分:AI的基础原理 什么是人工智能: 解释AI的定义和范畴。 介绍AI的历史和发展。 机器学习入门&#x…...
使用 Webpack 从 0 到 1 构建 Vue3 项目 + ts
使用 Webpack 从 0 到 1 构建 Vue3 项目 1.初始化项目结构2.安装 webpack,补充智能提示3.初步编写 webpack.config.js3.1设置入口文件及出口文件3.2 指定 html 模板位置 4.配置 运行/打包 命令,首次打包项目5.添加 Vue 及相关配置5.1安装并引入 vue5.2 补…...

【Git】Git 分支
Git 分支 1.分支简介 为了真正理解 Git 处理分支的方式,我们需要回顾一下 Git 是如何保存数据的。 或许你还记得 起步 的内容, Git 保存的不是文件的变化或者差异,而是一系列不同时刻的 快照 。 在进行提交操作时,Git 会保存一…...
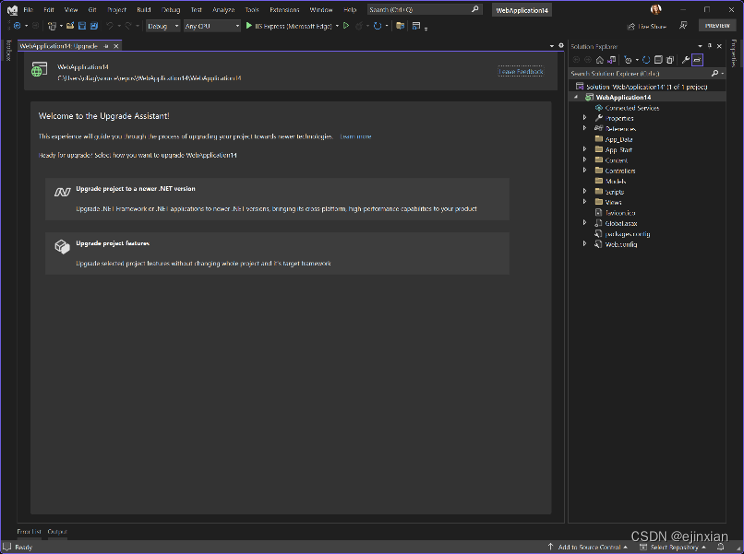
.NET Upgrade Assistant 升级 .NET MAUI
.NET Upgrade Assistant 是一种可帮助您将应用程序升级到最新的 .NET版本 的工具,并且您可以使用这个工具将您的应用程序从旧平台(例如 Xamarin Forms 和 UWP)迁移到新的平台。此外,这个新版本的工具,可以让您在不更改…...
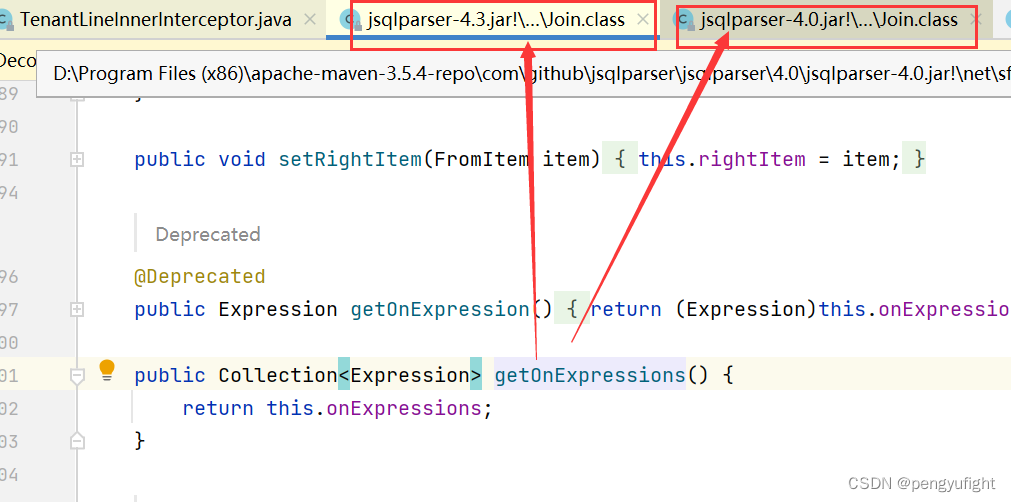
记一次诡异的Cannot find declaration to go to,Cannot resolve method
记一次诡异的 Cannot find declaration to go to, Cannot resolve method getOnExpressions in Join 对于项目中通常问题,清除缓存,重启idea,或者仔细检查语法通常都能解决问题,但是这次却失效了,以下是原…...
智慧园区:AI边缘计算技术与视频监控汇聚平台打造智慧园区解决方案
一、行业趋势与背景 智慧园区是现代城市发展的重要组成部分,通过智能化技术提高园区的运营效率、降低成本、增强环境可持续性等具有重要作用。在智慧园区中,人工智能和视频汇聚技术是重要的前置技术。人工智能技术可以实现对数据的智能化处理和分析&…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...
