徐亦达机器学习:Kalman Filter 卡尔曼滤波笔记 (一)

P ( x t P(x_t P(xt| x t − 1 ) x_{t-1}) xt−1) | P ( y t P(y_t P(yt| x t ) x_t) xt) | P ( x 1 ) P(x_1) P(x1) | |
|---|---|---|---|
| Discrete State DM | A X t − 1 , X t A_{X_{t-1},X_t} AXt−1,Xt | Any | π \pi π |
| Linear Gassian Kalman DM | N ( A X t − 1 + B , Q ) N(AX_{t-1}+B,Q) N(AXt−1+B,Q) | N ( H X t + C , R ) N(HX_t+C,R) N(HXt+C,R) | N ( μ 0 , ϵ 0 ) N(\mu_0,\epsilon_0) N(μ0,ϵ0) |
| No-Linear NoGaussian DM | f ( x t − 1 ) f(x_{t-1}) f(xt−1) | g ( y t ) g(y_t) g(yt) | f ( x 1 ) f(x_1) f(x1) |
{ P ( y 1 , . . . , y t ) − − e v a l u a t i o n a r g m e n t θ log P ( y 1 , . . . , y t ∣ θ ) − − p a r a m e t e r l e a r n i n g P ( x 1 , . . . , x t ∣ y 1 , . . . , y t ) − s t a t e d e c o d i n g P ( x t ∣ y 1 , . . , y t ) − f i l t e r i n g \left\{ \begin{aligned} P(y_1,...,y_t)--evaluation\\ argment \theta \log{P(y1,...,y_t|\theta)}--parameter learning \\ P(x_1,...,x_t|y_1,...,y_t)-state decoding \\ P(x_t | y_1,..,y_t)-filtering \end{aligned} \right. ⎩ ⎨ ⎧P(y1,...,yt)−−evaluationargmentθlogP(y1,...,yt∣θ)−−parameterlearningP(x1,...,xt∣y1,...,yt)−statedecodingP(xt∣y1,..,yt)−filtering
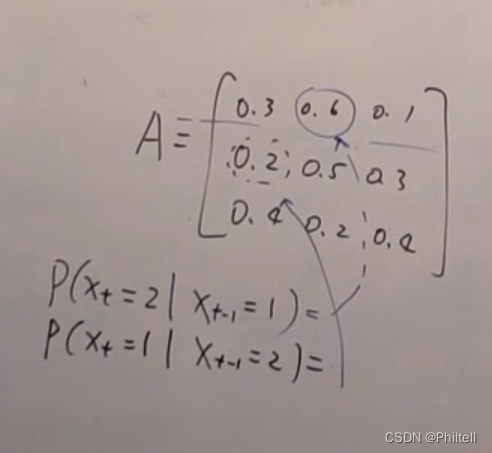
线性高斯噪声的动态模型
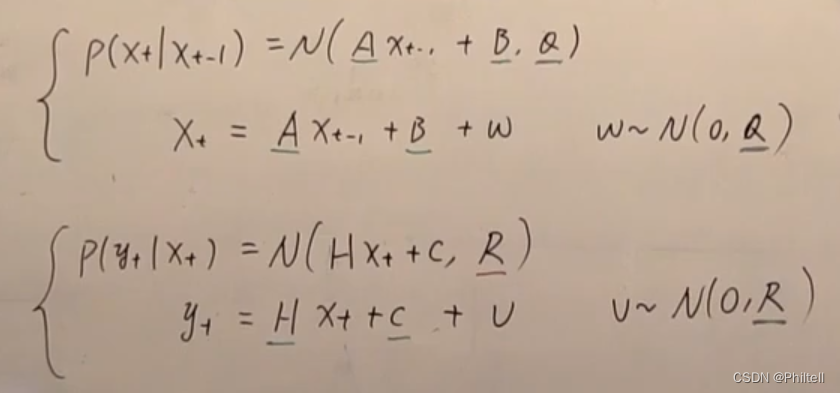
P ( x t ∣ y 1 , . . . , y t ) P(x_t|y_1,...,y_t) P(xt∣y1,...,yt)
假设转移概率是 P ( x t ∣ X t − 1 ) = N ( A X t − 1 + B , Q ) P(x_t|X_{t-1})= N(AX_{t-1}+B,Q) P(xt∣Xt−1)=N(AXt−1+B,Q)
X t = A X t − 1 + B + ω X_t = AX_{t-1}+B+\omega Xt=AXt−1+B+ω , ω ∼ N ( 0 , Q ) \omega \sim N(0,Q) ω∼N(0,Q)
measurement probility
P ( y t ∣ x t ) = N ( H X t + C , R ) P(y_t|x_t) = N(HX_t+C,R) P(yt∣xt)=N(HXt+C,R)
y t = H X t + C + v y_t = HX_t+C+v yt=HXt+C+v
v ∼ N ( 0 , R ) v \sim N(0,R) v∼N(0,R)
以下都是参数。
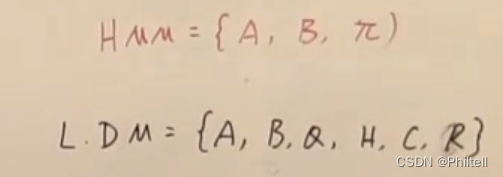
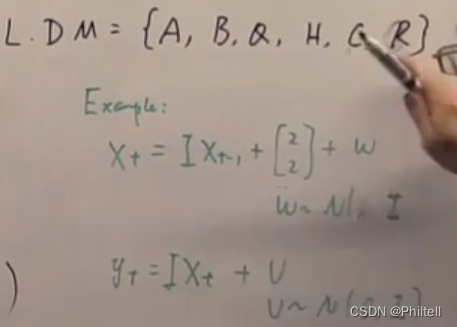


filter公式推导


HMM模型,当隐变量确定的时候,观测就变成独立的了。

- 卡尔曼滤波,当t = 1的时候,我们就知道 P ( x 1 ∣ y 1 ) ∼ N ( u ^ 1 , σ ^ 1 ) P(x_1|y_1) \sim N(\hat u_1,\hat \sigma_1) P(x1∣y1)∼N(u^1,σ^1)
- t = 2的时候, P ( x 2 ∣ y 2 ) ∼ N ( u ‾ 2 , σ ‾ 2 ) P(x_2|y_2) \sim N(\overline u_2,\overline \sigma_2) P(x2∣y2)∼N(u2,σ2)

个人理解
- 卡尔曼滤波可以理解为滤波器的一种,用数学表达就是用观测量 y 1 , y 2 , y 3 . . . , y t y_1,y_2,y_3...,y_t y1,y2,y3...,yt来获得t时刻的估计量 x t x_t xt,数学公式为
P ( x t ∣ y 1 , . . . , y t ) P(x_t|y_1,...,y_t) P(xt∣y1,...,yt)正比与 P ( x t , y 1 , . . . , y t ) P(x_t,y_1,...,y_t) P(xt,y1,...,yt)可以理解为前置条件 y 1 , . . . , y t y_1,...,y_t y1,...,yt发生的条件下有发生 x t x_t xt的概率与两类事件同时发生的概率是成正比的。可以简单理解为 P ( A ∣ B ) P(A|B) P(A∣B)与 P ( A , B ) P(A,B) P(A,B)成正比。 - 那么得出 P ( x t ∣ y 1 , . . . , y t ) ∝ P ( x t , y 1 , . . . , y t ) ∝ P ( y t ∣ x t , y 1 , . . . , y t − 1 ) ∗ P ( x t ∣ y 1 , . . . , y t − 1 ) P(x_t|y_1,...,y_t) \propto P(x_t,y_1,...,y_t) \propto P(y_t|x_t,y_1,...,y_{t-1}) * P(x_t|y_1,...,y_{t-1}) P(xt∣y1,...,yt)∝P(xt,y1,...,yt)∝P(yt∣xt,y1,...,yt−1)∗P(xt∣y1,...,yt−1)
- 有HMM可以得知, P ( y t ) P(y_t) P(yt)发生的概率是只跟 x t x_t xt相关,因此 P ( y t ∣ x t , y 1 , . . . , y t − 1 ) = P ( y t ∣ x t ) P(y_t|x_t,y_1,...,y_t-1) = P(y_t|x_t) P(yt∣xt,y1,...,yt−1)=P(yt∣xt),而 x t x_t xt的估计量,是通过上一次观测获得, x t x_t xt与 y 1 , . . . , y t − 1 y_1,...,y_{t-1} y1,...,yt−1相关。
- 那么得出预测为 P ( x t ∣ y 1 , . . . , y t − 1 ) P(x_t|y_1,...,y_{t-1}) P(xt∣y1,...,yt−1),前t-1时刻的观测值估计下一刻t的状态。
- 将 x t x_t xt看为常量,将 x t − 1 x_{t-1} xt−1看为变量,那么就得到了预测公式的推导公式为 P ( x t ∣ y 1 , . . . , y t − 1 ) = ∫ d ( x t − 1 ) P ( x t , x t − 1 ∣ y 1 , . . . , y t ) d x t − 1 ∝ ∫ x t − 1 P ( x t ∣ x t − 1 ) P ( x t − 1 ∣ y 1 , . . . , y t − 1 ) d ( x t − 1 ) P(x_t|y_1,...,y_{t-1})=\int_{d(x_{t-1})}{P(x_t,x_{t-1}|y_1,...,y_t)dx_{t-1}} \propto \int_{x_{t-1}}P(x_t|x_{t-1})P(x_{t-1}|y_1,...,y_{t-1})d(x_{t-1}) P(xt∣y1,...,yt−1)=∫d(xt−1)P(xt,xt−1∣y1,...,yt)dxt−1∝∫xt−1P(xt∣xt−1)P(xt−1∣y1,...,yt−1)d(xt−1)

总结
- 预测:不知道当前时刻的观测,用上一时刻观测与预测当前时刻的状态
P ( x t ∣ y 1 , . . . , y t − 1 ) = ∫ P ( x t ∣ x t − 1 ) P ( x t − 1 ∣ y 1 , . . . , y t − 1 ) P(x_t|y_1,...,y_{t-1})= \int P(x_t|x_{t-1})P(x_{t-1}|y_1,...,y_{t-1}) P(xt∣y1,...,yt−1)=∫P(xt∣xt−1)P(xt−1∣y1,...,yt−1) - 更新:已经知道当前时刻的观测,用当前的观测更新当前可是的状态
P ( x t ∣ y 1 , . . . , y t ) = P ( y t ∣ x t ) P ( x t ∣ y 1 , . . . , y t − 1 ) P(x_t|y_1,...,y_t)=P(y_t|x_t)P(x_t|y_1,...,y_{t-1}) P(xt∣y1,...,yt)=P(yt∣xt)P(xt∣y1,...,yt−1)



结论
- x t ∣ y 1 , . . . , y t − 1 = A E [ x t − 1 ] + A Δ X t − 1 + ω x_t|y_1,...,y_{t-1}=AE[x_{t-1}]+A\Delta X_{t-1}+\omega xt∣y1,...,yt−1=AE[xt−1]+AΔXt−1+ω = E [ x t ] + Δ x t =E[x_t]+\Delta x_t =E[xt]+Δxt
- y t ∣ y 1 , . . . y t − 1 = H A E [ X t − 1 ] + H A Δ x t − 1 + H ω + v = E [ y t ] + Δ y t y_t|y_1,...y_{t-1} = HAE[X_{t-1}]+HA \Delta x_{t-1}+H\omega + v = E[y_t] + \Delta y_t yt∣y1,...yt−1=HAE[Xt−1]+HAΔxt−1+Hω+v=E[yt]+Δyt
- P ( x t ∣ y 1 , . . . , y t ) = N ( A E [ x t − 1 ] , E [ ( Δ x ) ( Δ x ) T ] ) P(x_t|y_1,...,y_t) = N(AE[x_{t-1}],E[(\Delta x)(\Delta x)^T]) P(xt∣y1,...,yt)=N(AE[xt−1],E[(Δx)(Δx)T])
- P ( y t ∣ y 1 , . . . , y t − 1 ) = N ( H A E [ X t − 1 ] , E [ ( Δ y ) ( Δ y ) T ] ) P(y_t|y1,...,y_{t-1}) = N(HAE[X_{t-1}],E[(\Delta y)(\Delta y)^T]) P(yt∣y1,...,yt−1)=N(HAE[Xt−1],E[(Δy)(Δy)T])
以上为边缘分布
P ( x t , y t ∣ y 1 , . . . , y t − 1 ) P(x_t,y_t|y_1,...,y_{t-1}) P(xt,yt∣y1,...,yt−1)

非线性非高斯噪声的动态模型
相关文章:

徐亦达机器学习:Kalman Filter 卡尔曼滤波笔记 (一)
P ( x t P(x_t P(xt| x t − 1 ) x_{t-1}) xt−1) P ( y t P(y_t P(yt| x t ) x_t) xt) P ( x 1 ) P(x_1) P(x1)Discrete State DM A X t − 1 , X t A_{X_{t-1},X_t} AXt−1,XtAny π \pi πLinear Gassian Kalman DM N ( A X t − 1 B , Q ) N(AX_{t-1}B,Q)…...

Java和vue的包含数组组件contains、includes
List<String> tempList Arrays.asList("10018","1007","10017","1012"); if(tempList.contains(initMap.get("asset_type_id").toString())){// todo 计算运营终点桩号-起点桩号BigDecimal diffSum collectNum(col…...
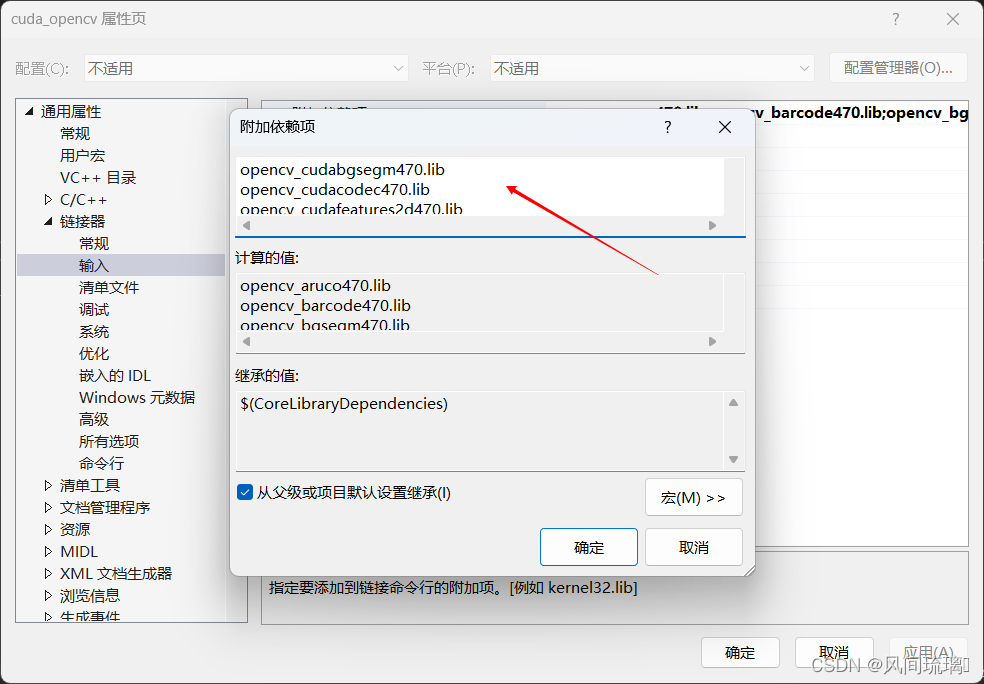
OpenCV_CUDA_VS编译安装
一、OpenCV 我这里是下载的OpenCV4.5.4,但是不知道到在vs里面build时一直报错,后面换了4.7.0的版本测试,安装成功。 Release OpenCV 4.5.4 opencv/opencv GitHub 这个里面有官方预编译好的OpenCV库,可以直接食用。 扩展包&am…...
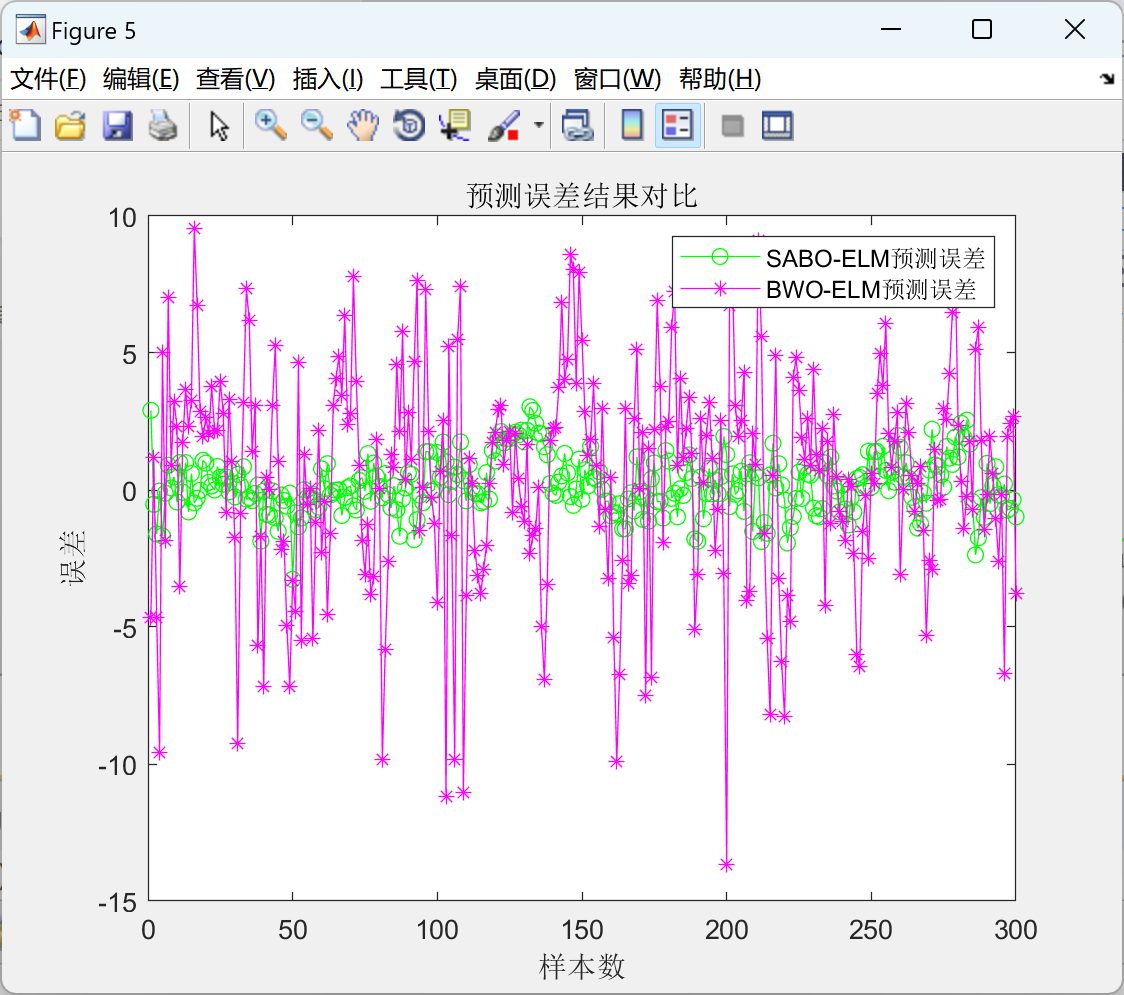
基于减法优化SABO优化ELM(SABO-ELM)负荷预测(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

记录第一个启动代码的诞生
核使用R52,参考汇编模板,一步一步来实现。 首先是ld文件,这个没啥好说的,主要是关注给vector_table划一块地址、stack地址,如下: .text.intvec :{_vectors_start .;KEEP(*(.text.intvec))_vectors_end .;…...
基于STM32的简化版智能手表
一、前言 本文的OLED多级菜单UI为一个综合性的STM32小项目,使用多传感器与OLED显示屏实现智能终端的效果。项目中的多级菜单UI使用了较为常见的结构体索引法去实现功能与功能之间的来回切换,搭配DHT11,RTC,LED,KEY等器…...

揭秘弹幕游戏制作
最近好多人问弹幕游戏,甚至是招人的也要DOTS做弹幕游戏... 实际上目前的弹幕游戏绝大多数应该和DOTS没有半点关系,别忘了DOTS这项技术渲染问题还没能够被合理解决呢 所以目前用的全都是GPU Instance这项技术,于是乎我决定下场写这篇帖子&am…...
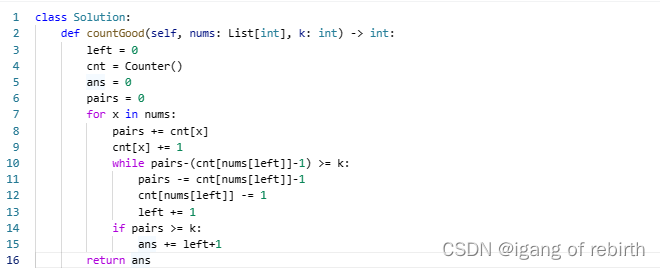
2327. 知道秘密的人数;1722. 执行交换操作后的最小汉明距离;2537. 统计好子数组的数目
2327. 知道秘密的人数 核心思想:动态规划,每天的人可以分为三种,可分享秘密的人,不可分享秘密的人,忘记秘密的人。定义f[i]为第i天可分享秘密的人,那么第(idelay ,iforget)天,会增加f[i]个可分…...
【TCPDF】使用TCPDF导出PDF文件
目录 一、安装TCPDF类库 二、安装字体 三、使用TCPDF导出PDF文件 目的:PHP通过TCPDF类库导出文件为PDF。 开发语言及类库:ThinkPHP、TCPDF 效果图如下 一、安装TCPDF类库 在项目根目录使用composer安装TCPDF,安装完成后会在vendor目录下…...

MacBook苹果电脑重装、降级系统
1、下载balenaEtcher镜像启动盘制作工具 https://tails.net/etcher/balenaEtcher-portable.exe 2、选择从文件烧录选择下载好的Mac 镜像文件 百度网盘 请输入提取码(Mac OS 10.10-12版本镜像文件) 第二步选择目标磁盘,这里需要准备一块1…...

Java 解决long类型数据在前后端传递失真问题
问题:雪花算法的id长度为19位,前端能够接收的数字最多只能是16位的,因此就会造成精度丢失,得到的ID不是真正的ID。 解决: 在拦截器中加入Long类型转换,返回给前端string package io.global.iot.common.c…...
IDEA的快捷键大全
快捷键 说明 IntelliJ IDEA 的便捷操作性,快捷键的功劳占了一大半,对于各个快捷键组合请认真对待。IntelliJ IDEA 本身的设计思维是提倡键盘优先于鼠标的,所以各种快捷键组合层出不穷,对于快捷键设置也有各种支持,对…...

简单记一下Vue router 路由中使用 vue-i18n 进行标题国际化
引入状态管理和国际化文件 import store from ../store import i18n from /configs/i18n使用状态管理设置路由当前国际化选项 // 使用状态管理 i18n.locale store.state.setStore.i18n??zh路由中使用i18n { path: /login, name: login, component: LoginPage, meta: { ti…...

【Gitea】 Post “http://localhost:3000/api/internal/hook/pre-receive/aa/bbb“ 异常
引 使用 JGit 做了一个发布代码到 Gitea 的接口,使用该接口发布代码到 http://xxx-local/{name}/{project} ,报了 Post "http://localhost:3000/api/internal/hook/pre-receive/{name}/{project} 相关的异常。具体内容如下: Gitea: In…...
如何使用element-ui相关组件如:el-select,el-table,el-switch,el-pagination,el-dialog
element-ui 官方链接: 组件 | Elementhttps://element.eleme.cn/#/zh-CN/component/installation el-select <!-- 用户类型选择框<template> 看情况使用value选择框绑定的值 命名必须是value不能改v-for"item in Options" options数据源来自于…...

微信小程序+echart实现点亮旅游地图
背景 最近看抖音有个很火的特效就是点亮地图,去过哪些地方,于是乎自己也想做一个,结合自己之前做的以家庭为单位的小程序,可以考虑做一个家庭一起点亮地图的功能。 效果图 过程 1,首先就是得去下微信小程序适配的ec…...
——Git命令总结)
Git(8)——Git命令总结
一、简介 本篇文章将基于Git(4)——Git命令小总结,补充后续的Git使用命令 二、总结 # 添加远程连接 git remote add origin 远端地址# 推送本地代码 git push origin 分支名称# 拉取远端代码(第一次) git clone 远端克隆地址# 更新远端代码…...

9.15 滴滴笔试
T1(二分) #include <bits/stdc.h>#define endl \nusing namespace std;typedef long long LL;const int N 1e5 10;int n, k; int a[N];bool check(int mid) {int rec 1e9, cnt 1;for(int i 0; i < n; i ) {int j i;while(j < n &…...
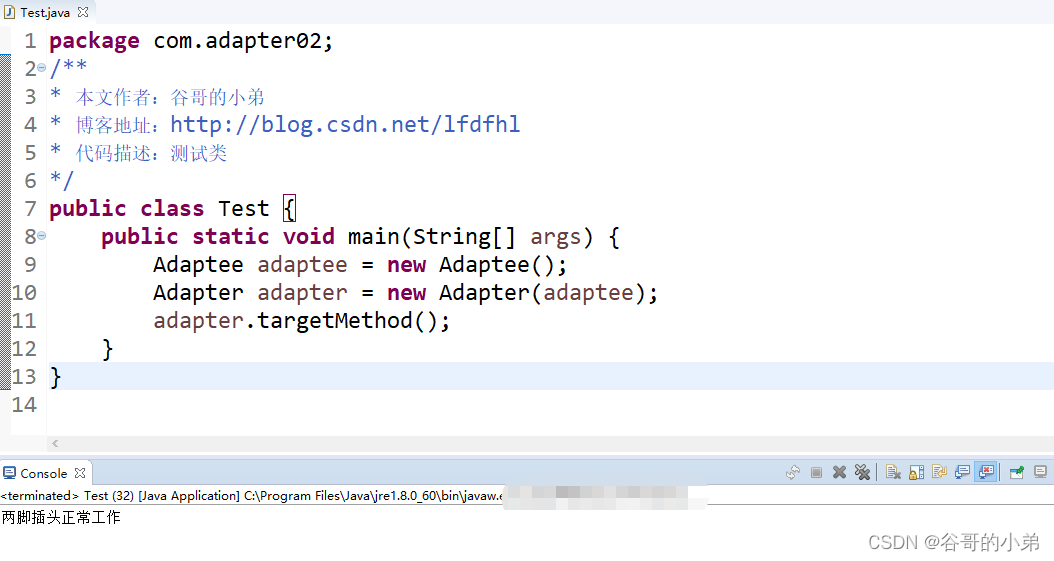
有趣的设计模式——适配器模式让两脚插头也能使用三孔插板
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl 场景与问题 众所周知,我们国家的生活用电的电压是220V而笔记本电脑、手机等电子设备的工作压没有这么高。为了使笔记本、手机等设备可以使用220V的生活用电就需…...
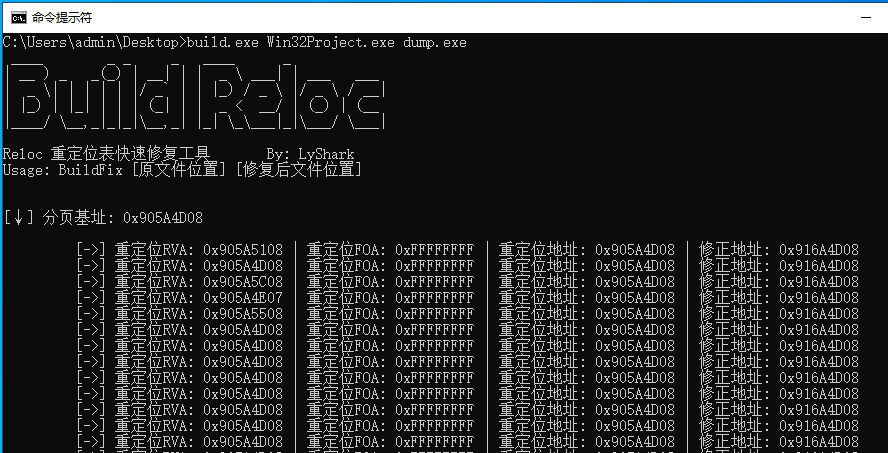
2.10 PE结构:重建重定位表结构
Relocation(重定位)是一种将程序中的一些地址修正为运行时可用的实际地址的机制。在程序编译过程中,由于程序中使用了各种全局变量和函数,这些变量和函数的地址还没有确定,因此它们的地址只能暂时使用一个相对地址。当…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...
