Attention is all you need 论文笔记
该论文引入Transformer,主要核心是自注意力机制,自注意力(Self-Attention)机制是一种可以考虑输入序列中所有位置信息的机制。
RNN介绍
引入RNN为了更好的处理序列信息,比如我 吃 苹果,前后的输入之间是有联系的。
如图:
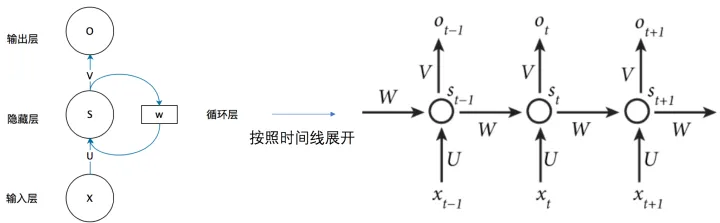
引入Transformer的原因
- 解决长距离依赖的问题:传统的RNN存在梯度消失和梯度爆炸的问题,难以有效捕获长距离依赖关系。而Transformer引入了注意力机制,使模型可以在序列中捕获远距离依赖关系。
- 并行计算:RNN和循环连接的特点使得它们难以并行计算,限制了计算速度。相比之下,Transformer模型的注意力机制允许模型在每个时间步骤上并行计算,大大加速计算速度。
- 可扩展性:Transformer模型可以适用与不同长度的序列
Attention函数分析
注意力机函数值注意力机制的核心组成部分,它定义了如何计算注意力权重,以及使用这些权重聚合数据来获取上下文表示。注意力函数包括:
- Query:查询用于确定关注哪些输入元素的向量或表示。在自注意力机制中,通常是前一个时间步骤的隐藏状态或者上下文表示。
- key:键是与输入元素相关的向量表示。注意力机制通过比较query和key的相似性来决定要关注哪些输入
- value:值是与键对应的输入元素的向量或表示。注意力机制根据query和key的相似性来为每个值分配权重,这些权重将用于生成上下文表示。
- score:分数表示key和query的相似性,分数越高表示查询更关注与键相关的输入。例如向量a和向量b,它的点积
,
越小,
越大,两个向量之间 相似性越高。
- 注意力权重:是一个概率分布,表示对每个输入元素的关注程度。通常由softmax得到,确保总和为1.
- 上下文表示:通过注意力权重对值进行加权求和得到,它是对输入元素的聚合表示,反应了模型的关注点。
注意力函数的一般计算步骤
- 计算query和key的相似性分数,通过点积、加性模型或者缩放点积等方式实现。
- 对相似性分数进行softmax操作,以此获得注意力权重,确保他们归一化为概率分布。
- 使用注意力权重对值加权求和,以此生成上下文表示。
对于自注意力机制来说
- query、key、value:自注意力的核心是通过三个线性变换来为每个位置生成这三个向量。这些向量在输入序列中的每个位置都有一个。对于给定的位置,query 用于提出问题,key 用于提供答案的位置信息,而value 包含了实际的信息。
- 计算注意力分数:计算分数通过将query和所有位置的key 进行点积操作得到的。注意力分户可以看成是度量两个位置之间关联性的分数,他表示了一个位置对于其他位置的关注程度。
- softmax 操作进行归一化:为了获得有效的注意力权重,对计算得到的注意力分数进行归一化处理。为了确保每个位置权重是有效的概率分布,从而更好的表达位置之间的关联性。
- 计算加权和:对得到的归一化之后的注意力权重和对应位置的value进行加权求和,得到每个位置的上下文表示。
多头注意力机制
是一种扩展的自注意力机制,它允许模型同时学习多个不同的关注模式。多头注意力机制将自注意力计算分为多个头,每个头学习不同的权重矩阵,以捕获不同类型的关联性。多个头的结果会拼接或合并,然后通过线性变换进行投影。
选择缩放点积原因
- 点积和加性注意力理论复杂度相似,但是在实践中点积注意力的速度更快、更节省空间,因为它可以使用高度优化的矩阵乘法代码来实现
- 对于键K的维度
越大,加性注意力的性能比点击好,所以我们怀疑对于很大的维度,点积会大幅度增长,为了抵消这种影响,我们使用缩小点积。
缩放点积
是注意力机制中一种常见的类型,通过和自注意力机制一起使用,它的目的是确保在计算注意力分数的时候,使得范围适中,避免梯度消失或者梯度爆炸。下面是介绍缩放点积的步骤:
- Query、Key、Value:这是缩放点积的三个输入,通常来自于一个序列。
- 相似性分数计算:计算查询和键之间的相似性。将查询和键之间的点积作为相似性分数。具体而言就是,对于给定的查询Q和键K,计算相似性分数矩阵为:
其中K^T表示键K的转置矩阵。每个Scores[i][j]表示查询的第i个元素和键的第j个元素的相似性。Score = Q*K^T - 缩放:为了稳定训练过程,缩放点积对相似性分数进行缩放操作,通过操作是除以一个缩放因子来实现。缩放因子通常是键K的维度
的平方根。即:
.缩放后的相似性分数Scale_Scores有助于控制梯度大小,防止梯度爆炸或者消失。
Scale_Scores = Scores / sqrt(d_k) - 计算注意力权重:对缩放后的相似性分数进行softmax操作,将其转化为概率分布,得到注意力权重。这些权重表示了对输入序列不同位置的关注程度。
attention_weight = softmax(Scale_Scores)
结论
在这项工作中,提出了 Transformer,这是一个完全基于注意力的序列转换模型。注意,用多头自注意力取代了编码器-解码器架构中最常用的递归层。
相关文章:
Attention is all you need 论文笔记
该论文引入Transformer,主要核心是自注意力机制,自注意力(Self-Attention)机制是一种可以考虑输入序列中所有位置信息的机制。 RNN介绍 引入RNN为了更好的处理序列信息,比如我 吃 苹果,前后的输入之间是有…...
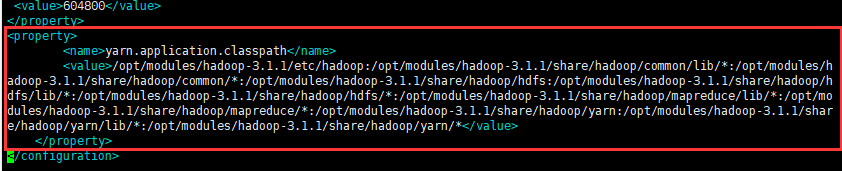
Hdoop伪分布式集群搭建
文章目录 Hadoop安装部署前言1.环境2.步骤3.效果图 具体步骤(一)前期准备(1)ping外网(2)配置主机名(3)配置时钟同步(4)关闭防火墙 (二)…...

java临时文件
临时文件 有时候,我们程序运行时需要产生中间文件,但是这些文件只是临时用途,并不做长久保存。 我们可以使用临时文件,不需要长久保存。 public static File createTempFile(String prefix, String suffix)prefix 前缀 suffix …...

C++中的<string>头文件 和 <cstring>头文件简介
C中的<string>头文件 和 <cstring>头文件简介 在C中<string> 和 <cstring> 是两个不同的头文件。 <string> 是C标准库中的头文件,定义了一个名为std::string的类,提供了对字符串的操作如size()、length()、empty() 及字…...

安装MySQL
Centos7下安装MySQL详细步骤_centos7安装mysql教程_欢欢李的博客-CSDN博客...

输入学生成绩,函数返回最大元素的数组下标,求最高分学生成绩(输入负数表示输入结束)
scanfscore()函数用于输入学生的成绩 int scanfscore(int score[N])//输入学生的成绩 {int i -1;do {i;printf("输入学生成绩:");scanf("%d", &score[i]);} while (score[i] > 0);return i; } findmax()用于寻找最大值 int findmax(int score[N…...

常用音频接口:TDM,PDM,I2S,PCM
常用音频接口:TDM,PDM,I2S,PCM_tdm音频_沙漠的甲壳虫的博客-CSDN博客 I2S/PCM接口及音频codec_音频pcm接口模块设计-CSDN博客 2个TDM8功放调试ing_周龙(AI湖湘学派)的博客-CSDN博客 数字音频接口时序----IIS、TDM、PCM、PDM_td…...
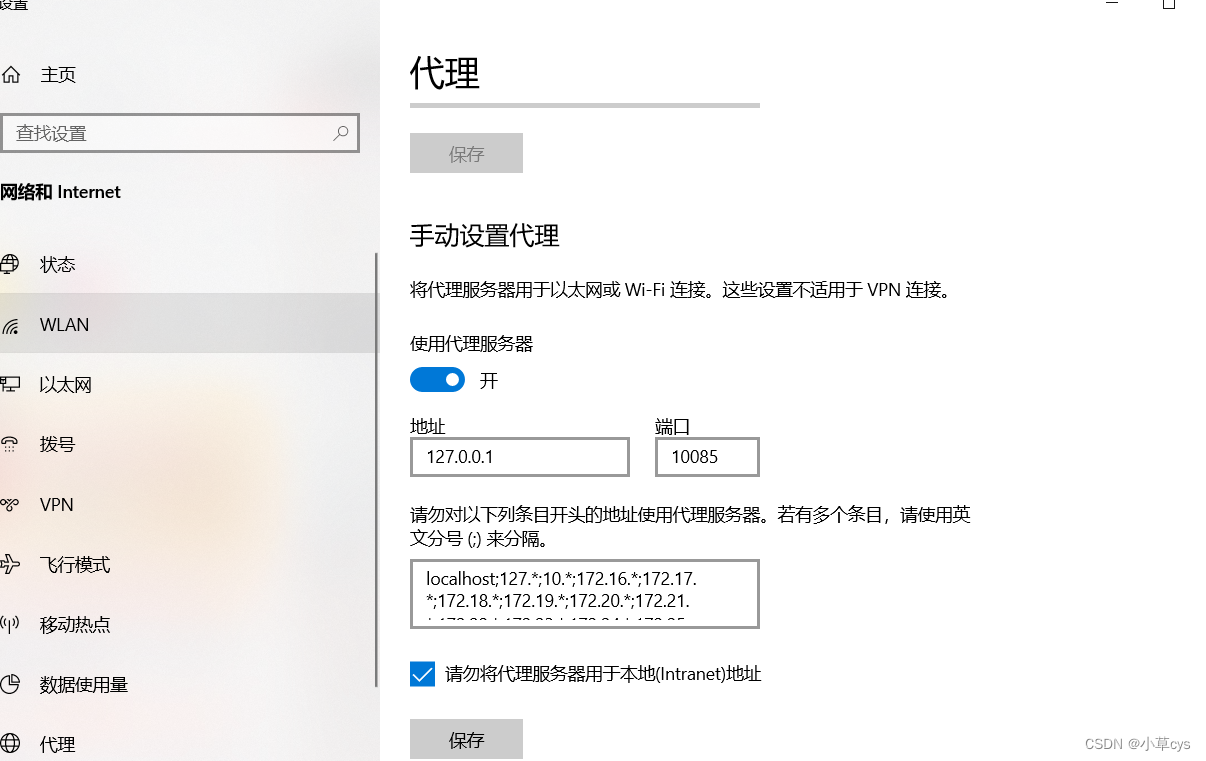
git clone报错Failed to connect to github.com port 443 after 21055 ms:
git 设置代理端口号 git config --global http.proxy http://127.0.0.1:10085 和 git config --global https.proxy http://127.0.0.1:10085 然后就可以成功git clone hugging face的数据集了 如果是https://huggingface.co/datasets/shibing624/medical/tree/main 那么…...
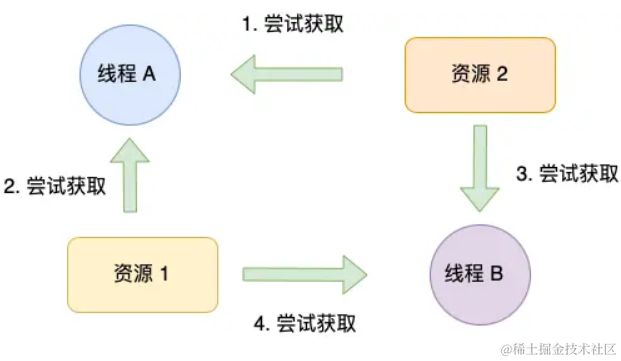
【操作系统】深入浅出死锁问题
死锁的概念 在多线程编程中,我们为了防止多线程竞争共享资源而导致数据错乱,都会在操作共享资源而导致数据错乱,都会在操作共享资源之前加上互斥锁,只有成功获得到锁的线程,才能操作共享资源,获取不到锁的…...

springboot实现webSocket服务端和客户端demo
1:pom导入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId><version>2.2.7.RELEASE</version></dependency>2:myWebSocketClien…...

代码走读: FFMPEG-ffplayer02
AVFrame int attribute_align_arg avcodec_receive_frame(AVCodecContext *avctx, AVFrame *frame) 选取一个音频解码器 和 一个视频解码器分别介绍该解码器功能 音频G722 g722dec.c -> g722_decode_frame 通过 ff_get_buffer 给 传入的 frame 指针分配内存 g722_decode_…...
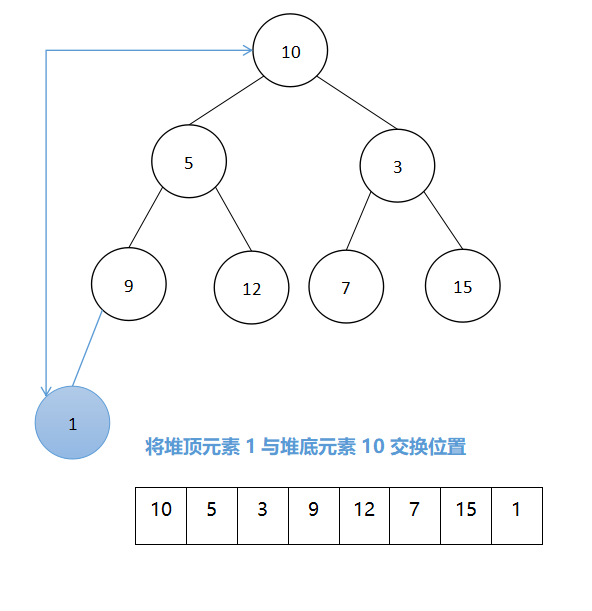
【数据结构】——排序算法的相关习题
目录 一、选择题题型一 (插入排序)1、直接插入排序2、折半插入排序3、希尔排序 题型二(交换排序)1、冒泡排序2、快速排序 题型三(选择排序)1、简单选择排序~2、堆排序 ~题型四(归并排序…...

C高级day5(Makefile)
一、Xmind整理: 二、上课笔记整理: 1.#----->把带参宏的参数替换成字符串 #include <stdio.h> #include <stdlib.h> #include <string.h> #define MAX(a,b) a>b?a:b #define STR(n) #n int main(int argc, const char *argv…...

Android 系统中适配OAID获取
一、OAID概念 OAID(Open Anonymous Identification)是一种匿名身份识别标识符, 用于在移动设备上进行广告追踪和个性化广告投放。它是由中国移动通信集 团、中国电信集团和中国联通集团共同推出的一项行业标准 OAID值为一个64位的数字 二、…...

差分数组leetcode 2770 数组的最大美丽值
什么是差分数组 差分数组是一种数据结构,它存储的是一个数组每个相邻元素的差值。换句话说,给定一个数组arr[],其对应的差分数组diff[]将满足: diff[i] arr[i1] - arr[i] 对于所有 0 < i < n-1 差分数组的作用 用于高效…...

请求响应状态码
请求与响应&状态码 Requests部分 请求行、消息报头、请求正文。 Header解释示例Accept指定客户端能够接收的内容类型Accept: text/plain, text/htmlAccept-Chars et浏览器可以接受的字符编码集。Accept-Charset: iso-8859-5Accept-Encodi ng指定浏览器可以支持的web服务…...

安卓机型系统美化 Color.xml文件必备常识 自定义颜色资源
color.xml文件是Android工程中用来进行颜色资源管理的文件.可以在color.xml文件中通过<color>标签来定义颜色资源.我们在布局文件中、代码中、style定义中或者其他资源文件中,都可以引用之前在color.xml文件中定义的颜色资源。 将color.xml文件拷到res/value…...
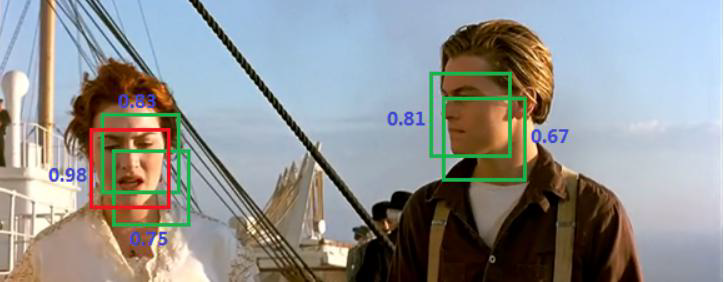
YOLO物体检测-系列教程1:YOLOV1整体解读(预选框/置信度/分类任/回归任务/损失函数/公式解析/置信度/非极大值抑制)
🎈🎈🎈YOLO 系列教程 总目录 YOLOV1整体解读 YOLOV2整体解读 YOLOV1提出论文:You Only Look Once: Unified, Real-Time Object Detection 1、物体检测经典方法 two-stage(两阶段):Faster-rc…...
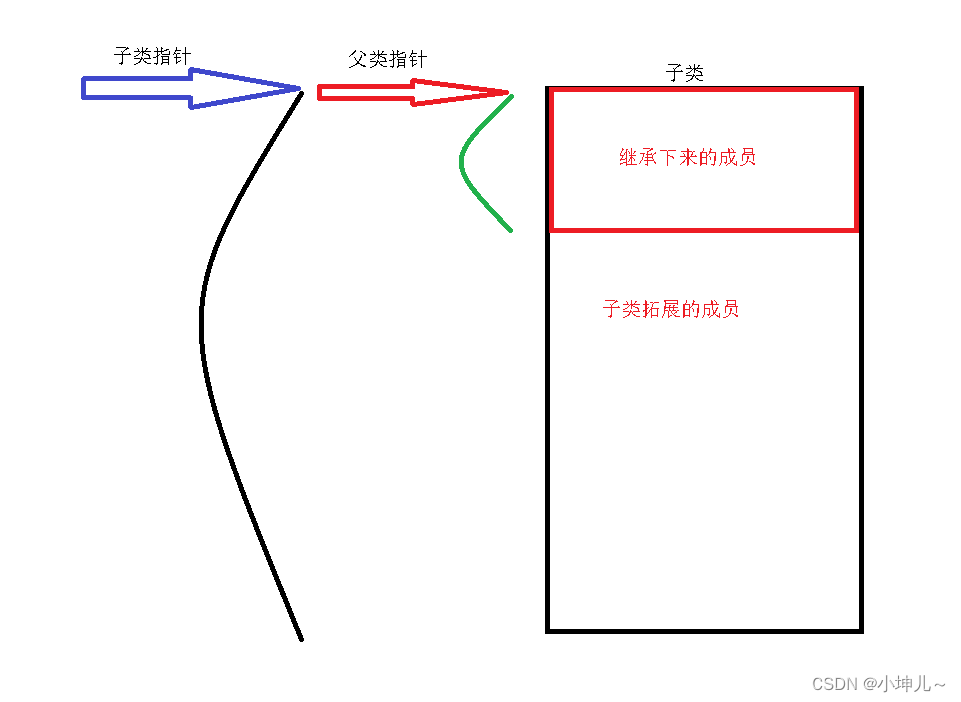
2023/9/12 -- C++/QT
作业 实现一个图形类(Shape),包含受保护成员属性:周长、面积, 公共成员函数:特殊成员函数书写 定义一个圆形类(Circle),继承自图形类,包含私有属性…...
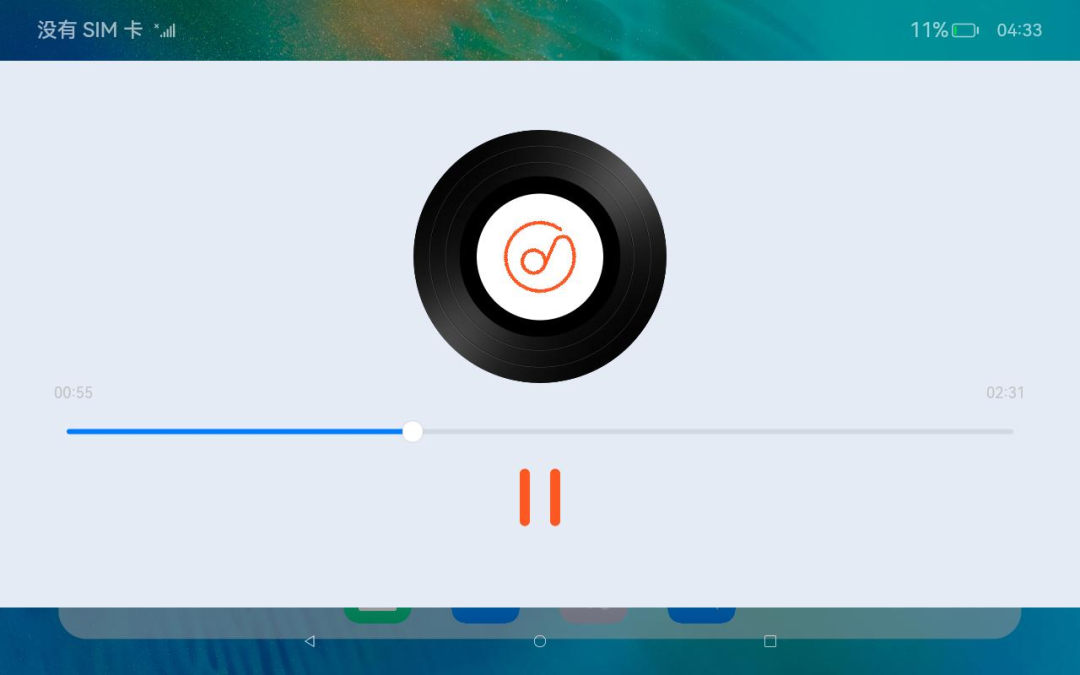
【Purple Pi OH RK3566鸿蒙开发板】OpenHarmony音频播放应用,真实体验感爆棚!
本文转载于Purple Pi OH开发爱好者,作者ITMING 。 原文链接:https://bbs.elecfans.com/jishu_2376383_1_1.html 01注意事项 DevEco Studio 4.0 Beta2(Build Version: 4.0.0.400) OpenHarmony SDK API 9 创建工程类型选择Appli…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
