Codeforces Round #836 (Div. 2)
A
SSeeeeiinngg DDoouubbllee
题意:告诉你一个字符串。若该串上每一位上的字母都可以出现两次,求回文串
思路:正向再反向输出s即可
#include <bits/stdc++.h>
#define lowbit(x) x&(-x)
#define ios cin.sync_with_stdio(false)
#define PII pair<int,int>
typedef long long ll;
const int N=1e6+10;
const int inf=0x3f3f3f3f;using namespace std;
int n;
string s;
void solve()
{cin>>s;cout<<s;reverse(s.begin(),s.end());cout<<s<<'\n';
}
int main()
{//ios;int _t=1;cin>>_t;while(_t--) solve();system("pause");return 0;
}B
XOR = Average
题意:让你构造长度为n的数组,满足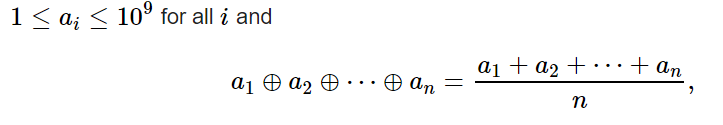
思路:n为奇数时,全为1
n为偶数时,两个元素为1和3,其余为2
#include <bits/stdc++.h>
#define lowbit(x) x&(-x)
#define ios cin.sync_with_stdio(false)
#define PII pair<int,int>
typedef long long ll;
const int N=1e6+10;
const int inf=0x3f3f3f3f;using namespace std;
int n;
int a[N];
void solve()
{cin>>n;if(n&1){for(int i=1;i<=n;i++) a[i]=1;}else {for(int i=3;i<=n;i++) a[i]=2;a[1]=1,a[2]=3;}for(int i=1;i<=n;i++)cout<<a[i]<<" \n"[i==n];
}
int main()
{//ios;int _t=1;cin>>_t;while(_t--) solve();system("pause");return 0;
}C
Almost All Multiples
题意:给定n和x,构造长度为n且字典序最小的排列。满足Pn=1,P1=x, i | Pi (1 <= i <= n-1)
思路:先不考虑字典序最小,当n%x==0时有解,让px=n,其他位置不变即可。n%x!=0时,假设我们在x的位置填k*x,那么k*x的位置要填p*k*x,若最后一个x倍数的位置不能填n就是无解的,即n%x!=0.
考虑字典序最小,x的位置我们先填2*x,要保证n是所填数的倍数且所填数未出现过,(否则到这个位置上的时候也无法用n替代那么也是不行的。)不行就填3*x,4*x...
#include <bits/stdc++.h>
#define lowbit(x) x&(-x)
#define ios cin.sync_with_stdio(false)
#define PII pair<int,int>
typedef long long ll;
const int N=1e6+10;
const int inf=0x3f3f3f3f;using namespace std;
int n,x;
int a[N];
bool vis[N];
void solve()
{cin>>n>>x;for(int i=1;i<=n;i++) vis[i]=0;if(n%x!=0){cout<<-1<<'\n';return ;}a[1]=x;a[n]=1;vis[x]=1;vis[1]=1;for(int i=2;i<n;i++){if(vis[i]){int cnt=2;while(n%(cnt*i)!=0&&!vis[cnt*i]&&cnt*i<=n) cnt++;a[i]=cnt*i;vis[cnt*i]=1;}else{a[i]=i;vis[i]=1;}}for(int i=1;i<=n;i++)cout<<a[i]<<" \n"[i==n];
}
int main()
{//ios;int _t=1;cin>>_t;while(_t--) solve();system("pause");return 0;
}D
Range = √Sum
题意: 给定长度n,让你构造长度为n且各元素不同,满足以下条件的数组
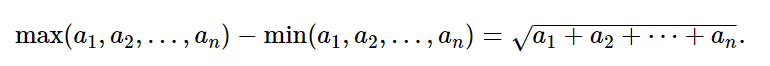
思路:n为偶数时,我们让元素为n+1,n-1,n+2,n-2,....n+n/2,n-n/2.极差为n且总和为n*n
n为奇数时,我们先让n+1变成偶数,用上述方法构造。然后删去元素n-1,再让其余n-1个元素都加一,这样极差和总和是未发生改变的。
#include <bits/stdc++.h>
#define lowbit(x) x&(-x)
#define ios cin.sync_with_stdio(false)
#define PII pair<int,int>
typedef long long ll;
const int N=1e6+10;
const int inf=0x3f3f3f3f;using namespace std;
int n;
void solve()
{cin>>n;vector<int>a;if(n%2==0){for(int i=1;i<=n/2;i++) cout<<n+i<<' ';for(int i=1;i<=n/2;i++) cout<<n-i<<' ';cout<<'\n';}else{for(int i=1;i<=(n+1)/2;i++) a.push_back(n+1+i);for(int i=2;i<=(n+1)/2;i++) a.push_back(n+1-i);for(int i=0;i<a.size();i++) cout<<a[i]+1<<" \n"[i==n-1];}
}
int main()
{//ios;int _t=1;cin>>_t;while(_t--) solve();system("pause");return 0;
}相关文章:
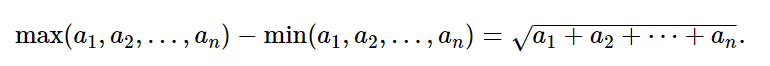
Codeforces Round #836 (Div. 2)
A SSeeeeiinngg DDoouubbllee 题意:告诉你一个字符串。若该串上每一位上的字母都可以出现两次,求回文串 思路:正向再反向输出s即可 #include <bits/stdc.h> #define lowbit(x) x&(-x) #define ios cin.sync_with_stdio(false)…...

Python学习之项目实践: 写一个MP3播放器
下面呢,是一个 Python MP3 播放器,它使用 pygame 模块来实现音乐播放功能: import pygame class MP3Player: """ MP3 播放器类 """ def __init__(self): pygame.mixer.init() def play(self, file_path): &quo…...
RocketMQTemplate 实现消息发送
代码托管于gitee:easy-rocketmq 文章目录一、前置工作二、消费者三、生产者1. 普通消息2. 过滤消息3. 同步消息4. 延时消息5. 批量消息6. 异步消息7. 单向消息8. 顺序消息9. 事务消息概要Demo源码解读一、前置工作 1、导入依赖 <dependency><groupId>…...

教师干货丨这5款微课必备提效神器,我要告诉全世界!
微课是一种短小精悍的视频教学形式,其设计和演示因特别简洁明了而被定义为“小而美”。由于只在几分钟时间内向学生传授所需知识,微课为学习者提供更多的选择机会和时间节约的便利,而这种趋势已经逐渐在新的社交媒体环境中显现出来。在制作微…...

timm使用swin-transformer
1.安装 pip install timm2.timm中有多少个预训练模型 #timm中有多少个预训练模型 model_pretrain_list timm.list_models(pretrainedTrue) print(len(model_pretrain_list), model_pretrain_list[:3])3加载swin模型一般准会出错 model_ft timm.create_model(swin_base_pat…...

【java基础】java八大基本数据类型和运算符
文章目录说明八大基本数据类型整型浮点型字符型布尔类型类型转换java运算符基础运算符二元运算符自增自减运算符关系和boolean运算符三元运算符位运算符运算符优先级说明 这里介绍java的八大基本数据类型和运算符 八大基本数据类型 java中有八大数据类型,4个整型…...

Mybatis源码学习笔记(四)之Mybatis执行增删改查方法的流程解析
1 Mybatis流程解析概述 Mybatis框架在执行增伤改的流程基本相同, 很简单,这个大家只要自己写个测试demo跟一下源码,基本就能明白是怎么回事,查询操作略有不同, 这里主要通过查询操作来解析一下整个框架的流程设计实现。 2 Mybat…...

浅谈测试用例设计
前言 最近干的最多的事情就是设计测试用例、评审测试用例了,于是我不禁又想到了一个经典的问题:如何设计出优秀的测试用例? 可能有些童鞋看到这个问题会有些不以为然,这有什么好想的?干个测试谁还不会设计测试用例&a…...
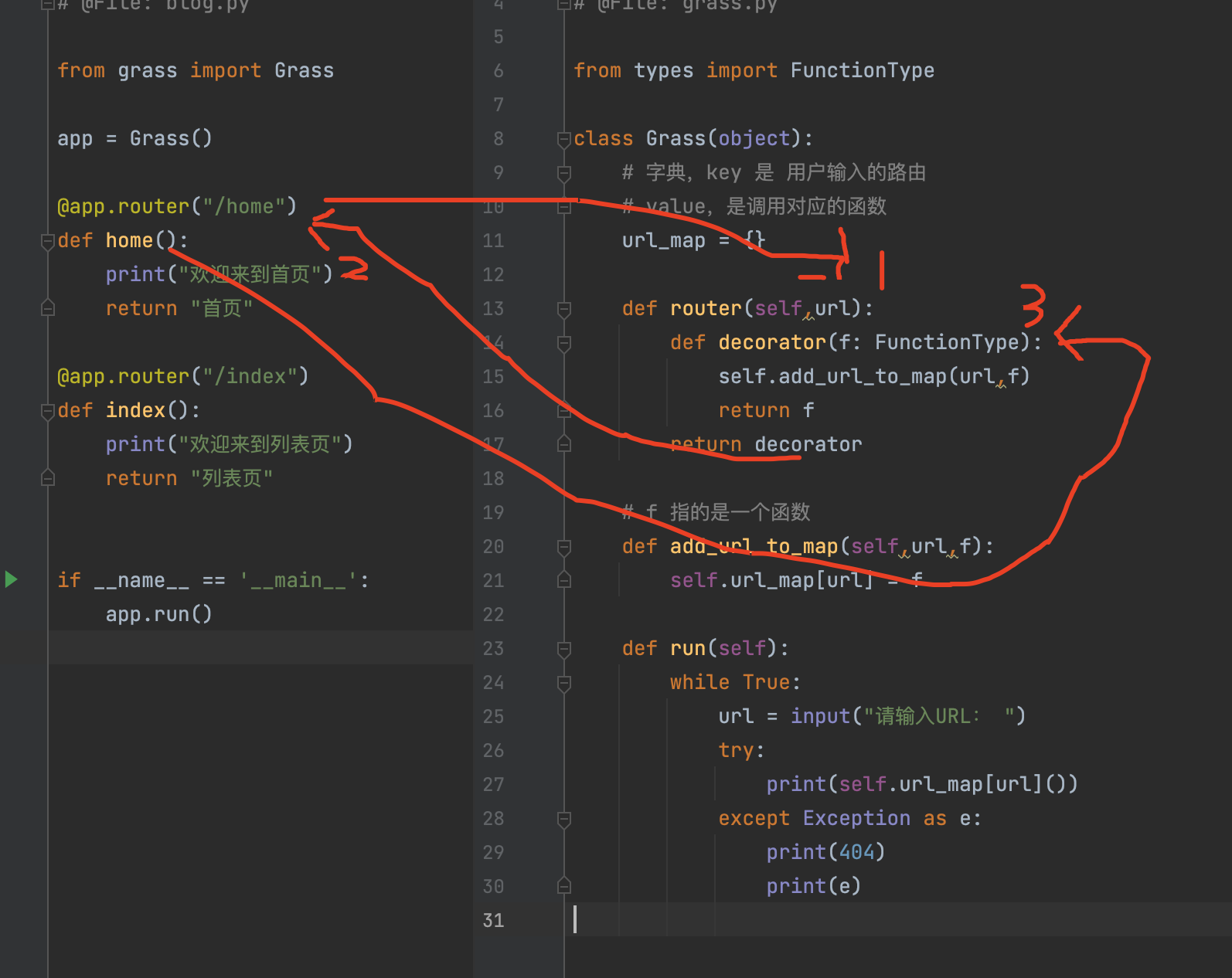
python 利用装饰器实现类似于flask路由
例子1: def f1():print(1111)def f2():print(2222)if __name__ __main__:print(33)打印结果: 33 在例子1中,f1() 与f2() 都没有被调用,只执行了print(33) f1与f2,是没有被调用的,但是如果f1 和 f2 上面…...
git 拉取远程分支到本地
目录:***!本小作者,是将终端和Git的可视化插件结合使用,刚接触的可以自习看一下,内容简单,避免弯路!***一,简单了解远程分支1,连接远程:2,提交&am…...

Answering Multi-Dimensional Range Queries under Local Differential Privacy
文章目录AbstractIntroduction2 PRELIMINARIES2.12.2 Categorical Frequency Oracles4 GRID APPROACHES4.1概述Abstract 在本文中,我们解决了在局部差异隐私下回答多维范围查询的问题。有三个关键的技术挑战:捕捉属性之间的相关性,避免维度的…...

手把手搭建springboot项目05-springboot整合Redis及其业务场景
目录前言一、食用步骤1.1 安装步骤1.1.1 客户端安装1.2 添加依赖1.3 修改配置1.4 项目使用1.5 序列化二、应用场景2.1 缓存2.2.分布式锁2.2.1 redis实现2.2.2 使用Redisson 作为分布式锁2.3 全局ID、计数器、限流2.4 购物车2.5 消息队列 (List)2.6 点赞、签到、打卡 (Set)2.7 筛…...
var、final、const、late)
Flutter基础语法(六)var、final、const、late
Flutter基础 第六章 Flutter关键字var、final、const、late的区别与使用 文章目录Flutter基础前言一、var1.var是什么?2.var如何使用3.var自动推断类型4.var可以再次赋值5.var指定类型二、final1.final是什么?2.final声明但不赋值3.final赋值多次4.final正常使用三、const1.…...
Linux之安装node
Linux之安装node步骤如下 1.去网站下载node 下载地址: https://npm.taobao.org/mirrors/ 2.上传到指定目录下 3.解压 tar -zxvf node-v17.3.0-linux-x644.配置node环境变量 //执行以下命令 vim /etc/profile //在path中加入以下内容 /usr/local/node-v15.14.0/b…...

二叉树、二叉搜索树、二叉树的最近祖先、二叉树的层序遍历【零神基础精讲】
来源0x3f:https://space.bilibili.com/206214 文章目录二叉树[104. 二叉树的最大深度](https://leetcode.cn/problems/maximum-depth-of-binary-tree/)[111. 二叉树的最小深度](https://leetcode.cn/problems/minimum-depth-of-binary-tree/)[129. 求根节点到叶节点…...

【算法】【数组与矩阵模块】求最长可整合子数组和子数组的长度
目录前言问题介绍解决方案代码编写java语言版本c语言版本c语言版本思考感悟写在最后前言 当前所有算法都使用测试用例运行过,但是不保证100%的测试用例,如果存在问题务必联系批评指正~ 在此感谢左大神让我对算法有了新的感悟认识! 问题介绍 …...

数据结构:循环队列的实现(leetcode622.设计循环队列)
目录 一.循环队列简单介绍 二.用静态数组实现循环队列 1.数组循环队列结构设计 2.数组循环队列的堆区内存申请接口 3.数据出队和入队的接口实现 4.其他操作接口 5.数组循环队列的实现代码总览 三.静态单向循环链表实现循环队列 1.链表循环队列的结构设计 2.创建静…...

[qiankun]实战问题汇总
[qiankun]实战问题汇总ERROR SyntaxError: Cannot use import statement outside a module问题分析解决方案子应用命名问题问题分析解决方案jsonpFunction详细错误信息问题分析解决方案微应用的注册问题Uncaught Error: application cli5-beta6-test-name died in status LOADI…...
:服务端常用参数配置)
Kafka(6):服务端常用参数配置
参数配置:config/server.properties # Licensed to the Apache Software Foundation (ASF) under one or more # contributor license agreements. See the NOTICE file distributed with # this work for additional information regarding copyright ownership.…...

2023爱分析·云原生智能运维中台市场厂商评估报告:秒云(miaoyun.io)
目录 1. 研究范围定义 2. 云原生智能运维中台市场定义 3. 厂商评估:秒云(miaoyun.io) 4. 入选证书 1. 研究范围定义 数字化时代,应用成为企业开展各项业务的落脚点。随着业务的快速发展,应用的功能迭代变得越…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
