Answering Multi-Dimensional Range Queries under Local Differential Privacy
文章目录
- Abstract
- Introduction
- 2 PRELIMINARIES
- 2.1
- 2.2 Categorical Frequency Oracles
- 4 GRID APPROACHES
- 4.1概述
Abstract
在本文中,我们解决了在局部差异隐私下回答多维范围查询的问题。有三个关键的技术挑战:捕捉属性之间的相关性,避免维度的诅咒,以及处理大范围的属性。现有的方法都不能令人满意地应对这三个挑战。克服这三个挑战,我们首先提出了一种称为二维网格(TDG)的方法。其主要思想是谨慎地使用装箱将所有属性对的二维(2-D)域划分为二维网格,该二维网格可以回答所有2-D范围查询。然而,为了减少噪声导致的误差,二维网格中的每个属性都需要粗粒度,从而丢失了各个属性的细粒度分布信息。为了纠正这一缺陷,我们进一步提出了混合维网格(HDG),它还引入了一维网格来捕获关于每个属性分布的更细粒度信息,并结合一维和二维网格的信息来回答范围查询。为了使HDG始终有效,我们基于对不同误差源如何受到这些选择影响的分析,为正确选择网格粒度提供了指导。在真实数据集和合成数据集上进行的大量实验表明,HDG可以比现有方法提供显著的改进。
Introduction
如今,用户的数据记录本质上包含许多顺序或数字属性,例如,收入、年龄、查看某个页面的时间、执行某个操作的次数等。这些属性的域由具有有意义的总顺序的值组成。对用户记录的一种典型的基本分析是多维范围查询,它是对感兴趣属性的多个谓词的结合,并询问其记录满足所有谓词的部分用户。特别是,谓词是对属性值范围的限制。然而,用户关于这些序数属性的记录是高度敏感的。如果没有强大的隐私保障,对其进行多维度的查询将危及个人隐私。因此,开发有效的方法来解决这些隐私问题成为迫切需要。
近年来,本地差别隐私(LDP)已成为个人隐私保护的事实标准。在LDP下,在将数据发送到中央服务器之前,在客户端添加随机噪声。因此,用户不需要依赖中央服务器的可信度。LDP的这一令人满意的特性已经导致了行业的广泛部署(例如,谷歌[16]、苹果[42]和微软[11])。然而,现有的LDP解决方案[9,31,48]大多限于对单个属性的一维(1-D)范围查询,并且不能很好地扩展到处理多维范围查询。
在本文中,我们解决了LDP下回答多维范围查询的问题。考虑到大量用户拥有包含多个序数属性的记录,不可信聚合器的目标是在满足LDP的同时,对用户的记录回答所有可能的多维范围查询。为了解决这个问题,我们确定了三个关键的技术挑战:1)如何捕捉属性之间的相关性,2)如何避免维度的诅咒,以及3)如何应对属性的大范围。任何未能解决这三个挑战中任何一个的方法都将具有较差的实用性。正如我们在第3节中所展示的,现有的方法或其扩展都不能同时应对所有三个挑战。
克服这三个挑战,我们首先提出了一种称为二维网格(TDG)的方法。其主要思想是谨慎地使用装箱将所有属性对的二维(2-D)域划分为2-D网格,该2-D网格可以回答所有可能的2-D范围查询。然而,为了减少噪声导致的误差,二维网格中的每个属性都需要粗粒度,从而丢失了各个属性的细粒度分布信息。当通过部分包含在查询中的单元格计算二维范围查询的答案时,需要假设这些单元格内的均匀分布,这可能会导致较大的错误。为了纠正这一缺陷,我们进一步提出了一种称为混合维网格(HDG)的升级方法,其核心思想是结合混合维(一维和二维)信息以获得更好的估计。特别是,HDG还引入了一维网格来捕获关于每个属性分布的更细粒度信息,并结合一维和二维网格的信息来回答范围查询。在TDG和HDG中,用户被分为多个组,每个组报告一个网格的信息。在LDP下收集每个网格中单元的频率后,聚合器使用技术来消除网格之间的负面性和不一致性,并最终使用这些网格来回答范围查询。
然而,使HDG始终有效仍然很重要,因为一维和二维网格的粒度可以直接影响HDG的性能。因此,有必要开发一种确定适当网格粒度的方法,以便HDG能够保证理想的效用。特别是在HDG中,有两个主要的误差来源:LDP的随机性质产生的噪声和装箱引起的误差。当值的分布是固定的时,由于均匀性假设,由于装箱引起的误差不会改变,并且可以被视为偏差,而由于噪声引起的误差可以被看作方差。因此,选择网格的粒度可以被视为一种偏差-方差权衡的形式。细粒度网格由于噪声而导致更大的误差,而粗粒度网格由于偏差而导致更高的误差。每种选择的效果都取决于隐私预算ε、人口和分布属性。通过深入分析这两个误差源,我们为在不同参数设置下正确选择网格粒度提供了指导。
通过通过二维网格捕获必要的成对属性相关性,这两种方法都克服了前两个挑战。此外,由于他们正确地使用了所提供的准则来减少由大域引起的错误,所以第三个挑战被仔细地解决了。因此,TDG通常比现有方法表现更好。通过引入一维网格来减少由于均匀性假设引起的误差,HDG可以比现有方法有显著的改进。
总之,本文做出了以下贡献:
-
我们提出了TDG和HDG来回答LDP下的多维范围查询,其中包括基于对不同来源的错误的分析来选择网格粒度的指南。
-
我们进行了大量实验,以使用真实和合成数据集评估不同方法的性能。结果表明,HDG优于现有方法一个数量级。
第2节提供了初步准备。第3节描述了问题陈述和四种基线方法。第4节详细介绍了网格方法。第5节显示了我们的实验结果。第6节审查相关工作。最后,第7节总结了本文。
2 PRELIMINARIES
2.1
2.2 Categorical Frequency Oracles
在LDP中,大多数问题可以归结为频率估计。
下面我们介绍了针对这些问题的两种最先进的分类频率Oracle(CFO)协议。
4 GRID APPROACHES
在本节中,我们首先在第4.1-4.4节中阐述了在LDP下回答多维范围查询的网格方法。然后我们在第4.5节中给出了他们的隐私和效用分析。最后,我们将在第4.6节中描述如何选择适当的粒度。
4.1概述
如第3节所分析,没有一种基线方法能够克服所有三个关键挑战。为了解决这个问题,我们首先提出了一种称为二维网格(TDG)的方法。其主要思想是谨慎地使用装箱将所有属性对的2-D域划分为2-D网格,该2-D网格可以回答所有2-D范围查询。
然而,由于网格中同一单元格内的值是一起报告的,因此聚合器无法告诉每个单元格内的分布,只能假设均匀分布。当通过部分包含在查询中的单元格计算2-D范围查询的答案时,由于一致性假设,这可能会导致较大的错误。为了纠正这一缺陷,我们进一步提出了一种称为混合维网格(HDG)的升级方法,该方法还引入了更细粒度的一维网格,并结合一维和二维网格的信息来回答范围查询。
请注意,前两个挑战带来了一个困境:捕获完全相关性(如HIO)将导致维度的诅咒;而仅关注个体属性(如MSW)将完全丢失相关信息。在CALM[57]中,通过使用二维边缘重建高维边缘,解决了类似的困境,这在处理这两个挑战时实现了很好的权衡。受此思想启发,TDG和HDG都选择通过二维网格捕获必要的成对属性相关性,这克服了前两个挑战。第三个挑战在TDG和HDG中也通过适当地使用与准则的合并来减少由大域引起的误差而被仔细地解决。
具体而言,TDG和HDG由三个阶段组成:
阶段1。构建网格。在TDG中,根据给定的d个属性,聚合器首先生成所有可能的m=C2d个属性对。然后聚合器将用户随机分成m个组,每组对应一对。接下来,对于其中1≤j<k≤d的每个属性对(aj,ak),聚合器通过将2-d域[c]×[c]划分为相等大小的д2×д2个2-d单元来分配相同的粒度д2以构建2-d网格G(j,k)。特别地,每个2-D单元指定由cд2×cд2-D值组成的2-D子域。
最后,为了获得每个网格中的小区的噪声频率,聚合器指示与网格对应的组中的每个用户使用OLH报告他/她的私有值在哪个小区中。
在HDG中,聚合器还分别为d个属性构造d个一维网格。因此HDG会有d+C2d个网格而且用户被划分为m=d+C2d个组,每个组对应于这些网格中的一个。除了建造C2dge粒度为g2的2D网格作为TDG,在HDG中,聚合器分配相同的粒度g1来构建一维网格G(j),其中包含每个单个属性aj(1≤j≤D)的大小相等的g1一维单元。特别地,每个一维单元指定由cд11-D值组成的一维子域。最后,如在TDG中一样,聚合器使用OLH来获得每个网格中小区的噪声频率。
阶段2。消除否定性和不一致性。由于使用OLH来确保隐私,小区的噪声频率可能是负的,这违反了真实频率为非负的先验知识。此外,由于属性与多个网格相关,不同网格中的属性上集成的噪声频率可能不同,从而导致网格之间的不一致。在这个阶段,为了提高效用,聚合器对构建的网格进行后处理,以消除负面性和不一致性。TDG和HDG的区别在于,TDG只需要聚合器处理2-D网格,而1-D和2-D网格需要在HDG中一起处理。我们在第4.2节中描述了后处理网格的细节。
阶段3。回答范围查询。在此阶段,聚合器可以回答所有多维范围查询。我们首先描述如何回答二维范围查询。为了便于说明,我们以对Aq0={a1,a2}感兴趣的二维范围查询q0为例。在TDG中,为了得到q0的答案fq0,聚合器首先找到与Aq0对应的2-D网格G(1,2),然后以以下方式检查G(1)中的所有2-D单元。如果小区完全包括在q0中,则聚合器将其噪声频率包括在fq0中;如果小区被部分地包括,则聚合器通过均匀猜测来估计小区和q0之间的公共2-D值的频率之和,即,假设小区内2-D值频率均匀分布,然后将该和与fq0相加。
在HDG中,聚合器使用响应矩阵而不是统一猜测来处理q0中部分包含的那些细胞,这可以显著提高结果的准确性。具体而言,对于每个属性对(aj,ak),聚合器首先使用三个网格{G(j),G(k),G,k)}在回答2-D范围查询之前构建响应矩阵M(j,k)。特别地,矩阵M(j,k)由c×c个元素组成,这些元素与(aj,ak)的2-D域[c]×[c]中2-D值的估计频率一一对应。第4.3节给出了响应矩阵生成的详细信息。当在HDG中计算2-D查询q0的答案fq0时,聚合器还检查网格G(1,2)中对应于Aq0的所有2-D单元。对于完全包括在q0中的小区,聚合器将其噪声频率包括在fq0中,如在TDG中;对于部分包含在查询q0中的单元格,聚合器识别该单元格与q0之间的公共2-D值,然后将M(1,2)中它们的对应元素的和与fq0相加。
对于λ>2的λ-D范围查询,其答案不能直接从构建的二维网格或响应矩阵中获得。为了回答这个λ-D查询,我们建议将其分为?λ 2 ? 关联的二维范围查询,然后从这些答案中估计其答案?λ 2 ? 二维查询。我们将在第4.4节中详细讨论。
相关文章:

Answering Multi-Dimensional Range Queries under Local Differential Privacy
文章目录AbstractIntroduction2 PRELIMINARIES2.12.2 Categorical Frequency Oracles4 GRID APPROACHES4.1概述Abstract 在本文中,我们解决了在局部差异隐私下回答多维范围查询的问题。有三个关键的技术挑战:捕捉属性之间的相关性,避免维度的…...

手把手搭建springboot项目05-springboot整合Redis及其业务场景
目录前言一、食用步骤1.1 安装步骤1.1.1 客户端安装1.2 添加依赖1.3 修改配置1.4 项目使用1.5 序列化二、应用场景2.1 缓存2.2.分布式锁2.2.1 redis实现2.2.2 使用Redisson 作为分布式锁2.3 全局ID、计数器、限流2.4 购物车2.5 消息队列 (List)2.6 点赞、签到、打卡 (Set)2.7 筛…...
var、final、const、late)
Flutter基础语法(六)var、final、const、late
Flutter基础 第六章 Flutter关键字var、final、const、late的区别与使用 文章目录Flutter基础前言一、var1.var是什么?2.var如何使用3.var自动推断类型4.var可以再次赋值5.var指定类型二、final1.final是什么?2.final声明但不赋值3.final赋值多次4.final正常使用三、const1.…...
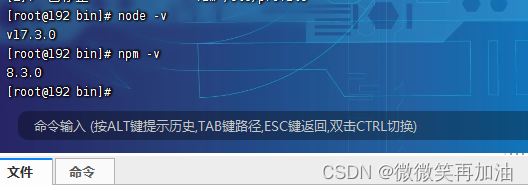
Linux之安装node
Linux之安装node步骤如下 1.去网站下载node 下载地址: https://npm.taobao.org/mirrors/ 2.上传到指定目录下 3.解压 tar -zxvf node-v17.3.0-linux-x644.配置node环境变量 //执行以下命令 vim /etc/profile //在path中加入以下内容 /usr/local/node-v15.14.0/b…...

二叉树、二叉搜索树、二叉树的最近祖先、二叉树的层序遍历【零神基础精讲】
来源0x3f:https://space.bilibili.com/206214 文章目录二叉树[104. 二叉树的最大深度](https://leetcode.cn/problems/maximum-depth-of-binary-tree/)[111. 二叉树的最小深度](https://leetcode.cn/problems/minimum-depth-of-binary-tree/)[129. 求根节点到叶节点…...

【算法】【数组与矩阵模块】求最长可整合子数组和子数组的长度
目录前言问题介绍解决方案代码编写java语言版本c语言版本c语言版本思考感悟写在最后前言 当前所有算法都使用测试用例运行过,但是不保证100%的测试用例,如果存在问题务必联系批评指正~ 在此感谢左大神让我对算法有了新的感悟认识! 问题介绍 …...

数据结构:循环队列的实现(leetcode622.设计循环队列)
目录 一.循环队列简单介绍 二.用静态数组实现循环队列 1.数组循环队列结构设计 2.数组循环队列的堆区内存申请接口 3.数据出队和入队的接口实现 4.其他操作接口 5.数组循环队列的实现代码总览 三.静态单向循环链表实现循环队列 1.链表循环队列的结构设计 2.创建静…...

[qiankun]实战问题汇总
[qiankun]实战问题汇总ERROR SyntaxError: Cannot use import statement outside a module问题分析解决方案子应用命名问题问题分析解决方案jsonpFunction详细错误信息问题分析解决方案微应用的注册问题Uncaught Error: application cli5-beta6-test-name died in status LOADI…...
:服务端常用参数配置)
Kafka(6):服务端常用参数配置
参数配置:config/server.properties # Licensed to the Apache Software Foundation (ASF) under one or more # contributor license agreements. See the NOTICE file distributed with # this work for additional information regarding copyright ownership.…...

2023爱分析·云原生智能运维中台市场厂商评估报告:秒云(miaoyun.io)
目录 1. 研究范围定义 2. 云原生智能运维中台市场定义 3. 厂商评估:秒云(miaoyun.io) 4. 入选证书 1. 研究范围定义 数字化时代,应用成为企业开展各项业务的落脚点。随着业务的快速发展,应用的功能迭代变得越…...

hadoop容器化部署
1、原容器 java:openjdk-8u111-jre jre路径: /usr/lib/jvm/java-8-openjdk-amd64 /usr/lib/jvm/java-1.8.0-openjdk-amd64 2、安装ssh docker run -it --name hadoop-test java:openjdk-8u111-jre bash apt-get update apt-get install openssh service ssh start …...
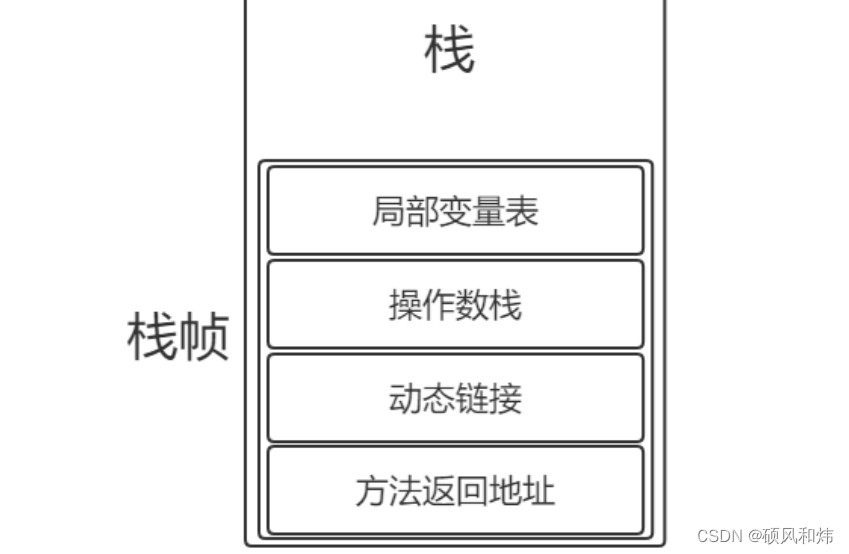
【07-JVM面试专题-JVM运行时数据区的虚拟机栈你知道吗?它的基本结构是什么呢?你知道栈帧的结构吗?那你说说动态链接吧?】
JVM运行时数据区的虚拟机栈你知道吗?它的基本结构是什么呢?你知道栈帧的结构吗?那你说说动态链接吧? JVM运行时数据区的虚拟机栈你知道吗?它的基本结构是什么呢?你知道栈帧的结构吗?那你说说动态…...

Java性能优化-GC优化基础
GC优化基础 调整堆大小 如果在FULL GC系统进行了交换,停顿时间会增长几个数量级,OS 如果G1 GC和后台进程处理堆,将会出现等待数据从磁盘复制到主内存时间较长,速度和下降并且并发模式可能失效 linux 关闭交换区 swapoff -a linu…...
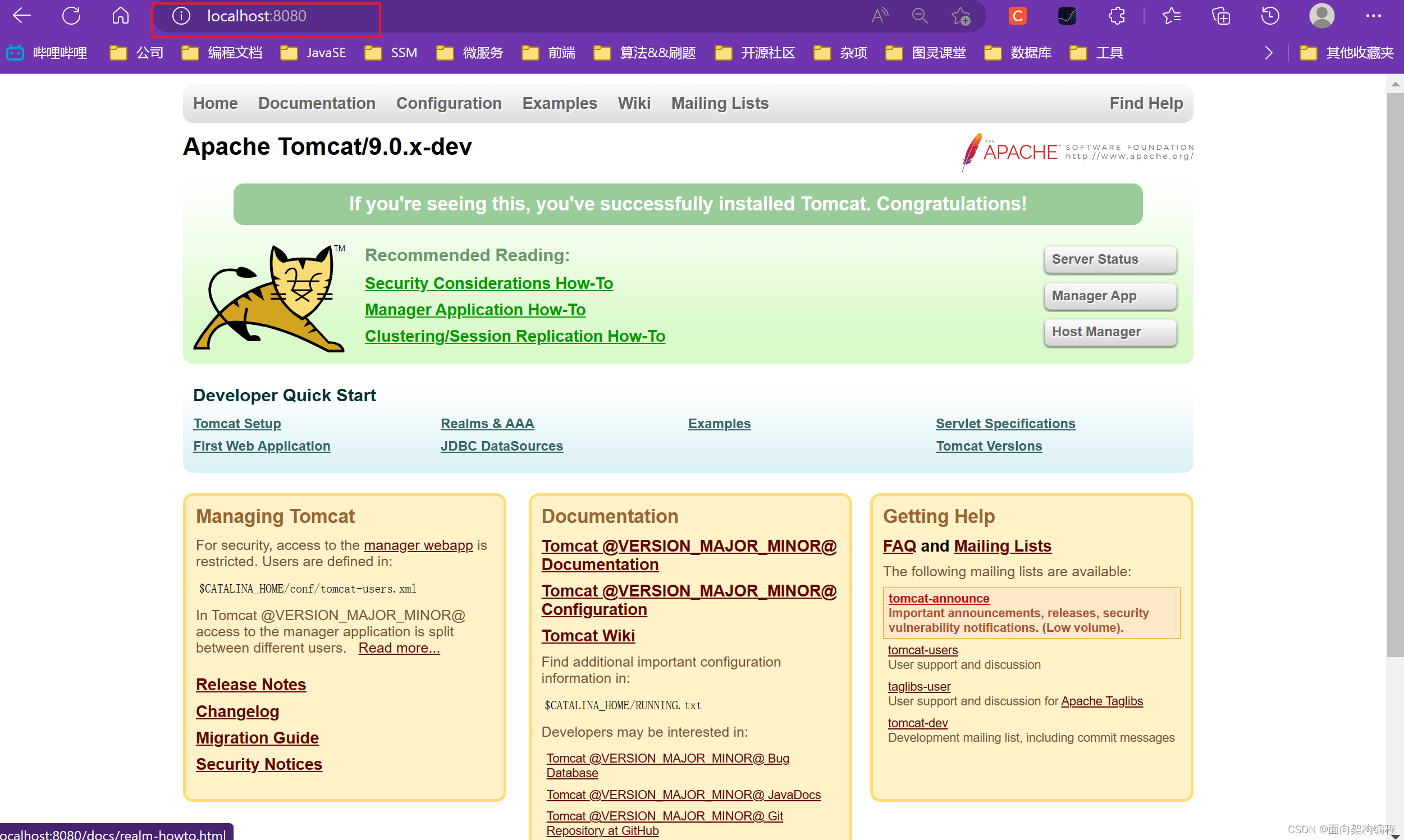
【Tomcat】IDEA编译Tomcat源码-手把手教程
一、环境准备Tomcat不同版本之间有一定的兼容性问题~如下图所示:官网地址:https://tomcat.apache.org/whichversion.html下载tomcat9官网上面的源码:这一篇文章主要是带着大家在自己的IDEA跑起来一个Tomcat。使用的版本是Tomcat9.0.55 和 JDK…...
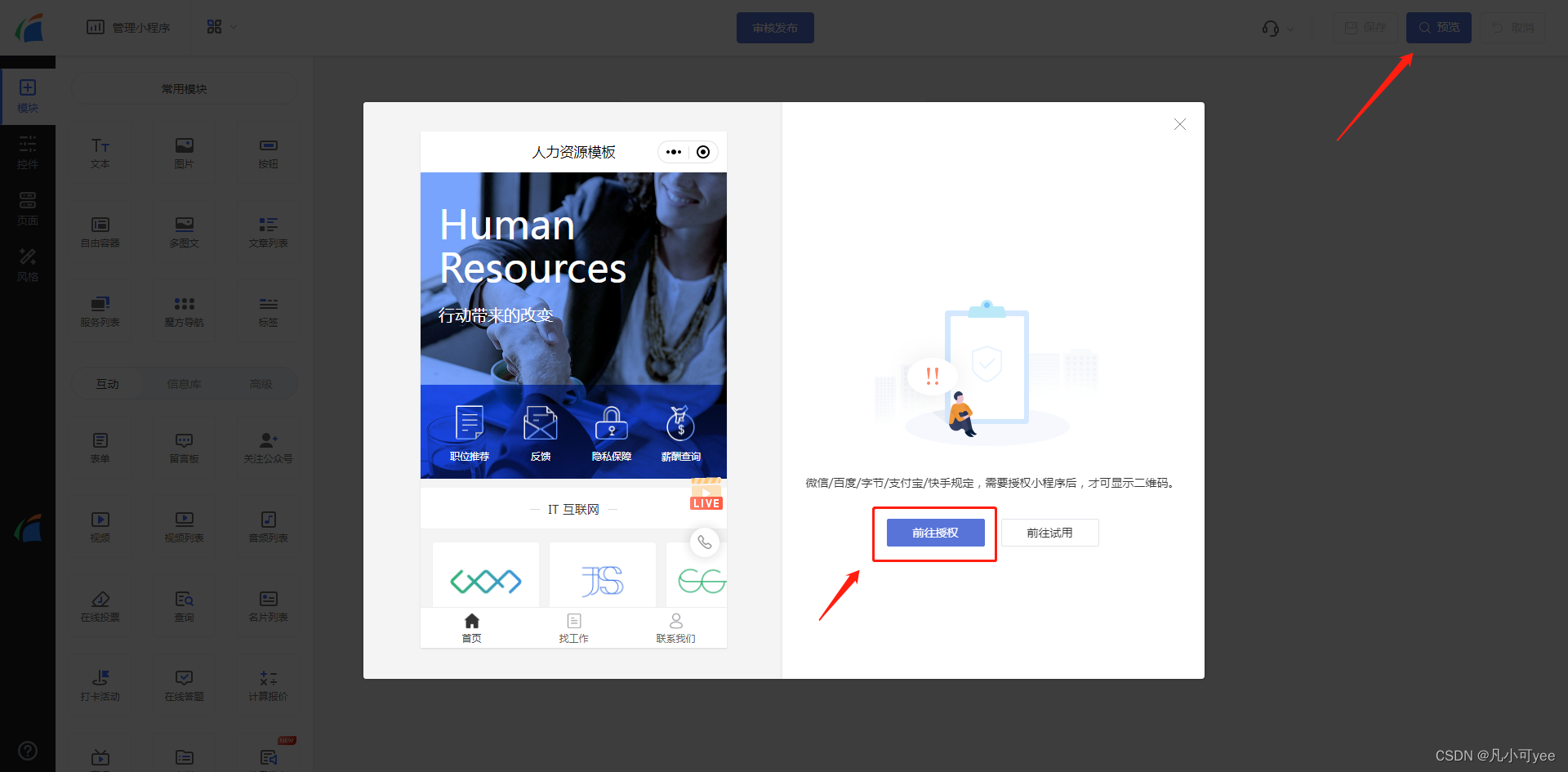
如何弄小程序?公司企业可以这样做小程序
公司企业现在对于小程序的需求已经是刚需了,即使已经有官网的情况下,也会考虑再弄一个小程序来做小程序官网。那么公司企业如何弄小程序呢?下面跟大家说说方法。 流程一、找小程序服务商 由于一些公司企业并不像现在的互联网公司企业那样有…...
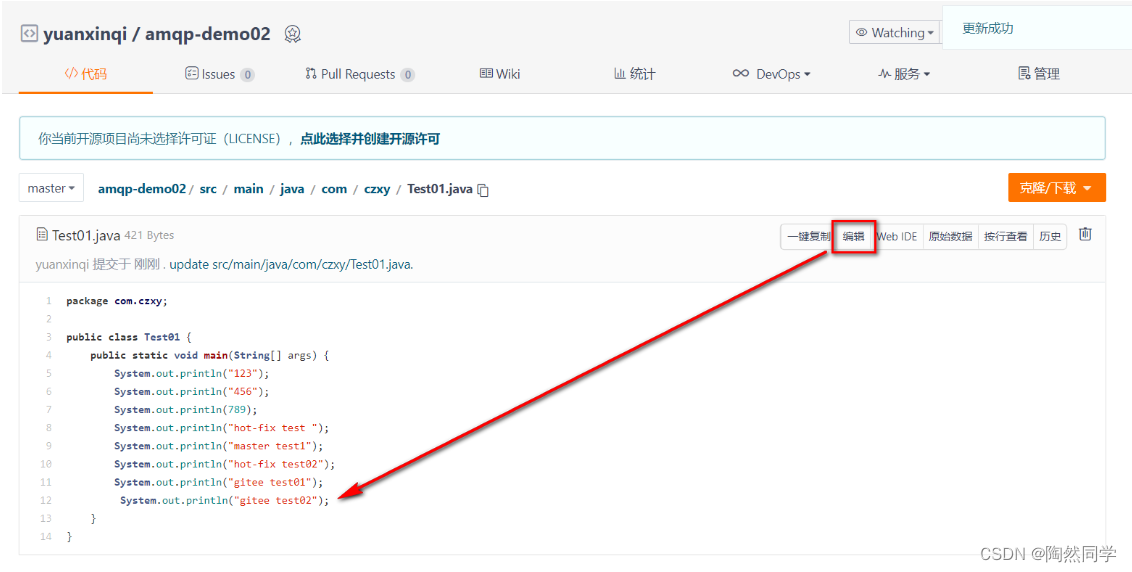
【Git】IDEA集合Git和码云
目录 7、IDEA集合Git 7.1 配置Git忽略文件-IDEA特定文件 7.2 定位 Git 程序 7.3 初始化本地库 7.4 添加到暂存区 7.5 提交到本地库 7.6 切换版本 7.7 创建分支 7.8 切换分支 7.9 合并分支 7.10 解决冲突 8、 Idea集成码云 8.1 IDEA 安装码云插件 8.2 分析工程到码…...
)
[USACO03FALL / HAOI2006] 受欢迎的牛 G(C++,强连通分量)
题目背景 本题测试数据已修复。 题目描述 每头奶牛都梦想成为牛棚里的明星。被所有奶牛喜欢的奶牛就是一头明星奶牛。所有奶牛都是自恋狂,每头奶牛总是喜欢自己的。奶牛之间的“喜欢”是可以传递的——如果 AAA 喜欢 BBB,BBB 喜欢 CCC,那么…...

Vue 动态路由接口数据结构化为符合VueRouter的声明结构及菜单导航结构、动态路由懒加载方法
Vue 动态路由接口数据结构化为符合VueRouter的声明结构及菜单导航结构、动态路由懒加载方法 实现目标 项目打包代码实现按需分割路由懒加载按需打包,排除引入子组件的冗余打包(仅处理打包冗余现象,不影响生产部署)解决路由懒加载…...
Python----------字符串
1.转义字符 注:转义字符放在你所想效果字符前 2.原始字符串 print(r"D:\three\two\one\now") ->D:\three\two\one\now注: 在使用原始字符串时,转义字符不再有效,只能当作原始的字符,每个字符都没有特殊…...
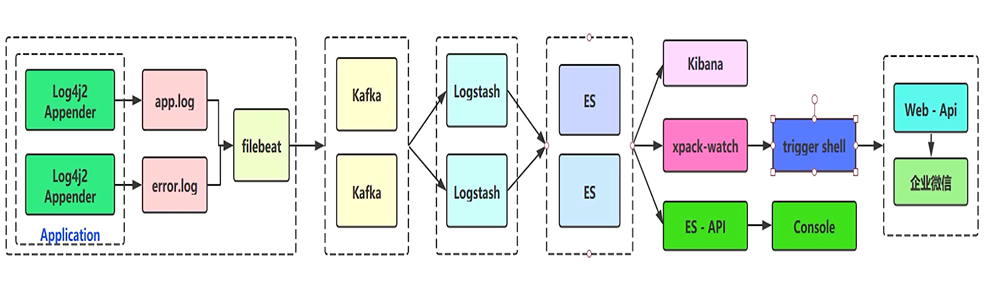
日志收集笔记(架构设计、Log4j2项目初始化、Lombok)
1 架构设计 ELK 技术栈架构设计图: 从左往右看, Beats:主要是使用 Filebeat,用于收集日志,将收集后的日志数据发送给 Kafka,充当 Kafka 的生产者Kafka:高性能消息队列,主要起缓冲…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...
