简单介绍神经网络中不同优化器的数学原理及使用特性【含规律总结】
当涉及到优化器时,我们通常是在解决一个参数优化问题,也就是寻找能够使损失函数最小化的一组参数。当我们在无脑用adam时,有没有斟酌过用这个是否合适,或者说凭经验能够有目的性换用不同的优化器?是否用其他的优化器可以更好的解决问题?那我就介绍解释几种常用的优化器的基本原理:
-
随机梯度下降(SGD):
SGD 是最基本的优化算法之一。它通过计算当前位置的梯度(即损失函数对参数的导数),然后朝着梯度的反方向更新参数。数学上可以表示为:
w = w − α ⋅ ∇ J ( w ) w=w−α⋅∇J(w) w=w−α⋅∇J(w)
其中, w w w 是待优化的参数, α \alpha α 是学习率, ∇ J ( w ) \nabla J(w) ∇J(w) 是损失函数关于参数的梯度。
-
动量优化器(Momentum):
Momentum 在 SGD 的基础上引入了动量项,它可以理解为模拟物体在空间中运动的物理量。这个动量项会考虑之前的更新,从而使更新方向在一定程度上保持一致。数学上可以表示为:
v = β ⋅ v + ( 1 − β ) ⋅ ∇ J ( w ) v=\beta⋅v+(1−\beta)⋅ \nabla J(w) v=β⋅v+(1−β)⋅∇J(w)
w = w − α ⋅ v w=w−α⋅v w=w−α⋅v
其中, v v v 是动量, β \beta β 是动量因子,控制之前更新的影响程度。
-
AdaGrad:
AdaGrad 是自适应学习率的一种算法。它会根据参数的历史梯度调整学习率,使得对于稀疏数据来说可以使用一个更大的学习率,而对于频繁出现的数据则会使用较小的学习率。数学上可以表示为:
w = w − α G + ϵ ⋅ ∇ J ( w ) w = w - \frac{\alpha}{\sqrt{G + \epsilon}} \cdot \nabla J(w) w=w−G+ϵα⋅∇J(w)
其中, G G G 是梯度的平方和的累积, ϵ \epsilon ϵ 是一个很小的数,防止除零错误。
-
RMSprop:
RMSprop 是 AdaGrad 的一个变体,它引入了一个衰减系数 β \beta β,用来控制历史梯度的权重。这使得 RMSprop 更加平滑地调整学习率。数学上可以表示为:
G = β ⋅ G + ( 1 − β ) ⋅ ( ∇ J ( w ) ) 2 G = \beta \cdot G + (1 - \beta) \cdot (\nabla J(w))^2 G=β⋅G+(1−β)⋅(∇J(w))2
w = w − α G + ϵ ⋅ ∇ J ( w ) w = w - \frac{\alpha}{\sqrt{G + \epsilon}} \cdot \nabla J(w) w=w−G+ϵα⋅∇J(w)
其中, G G G 是平方梯度的指数加权移动平均。
-
Adam:
Adam 结合了 Momentum 和 RMSprop 的特性,是一种同时考虑动量和自适应学习率的优化器。它可以动态地调整每个参数的学习率,并且可以保持更新方向的一致性。Adam 还引入了偏差修正,以解决初始训练时的偏差问题。数学上可以表示为:
m = β 1 ⋅ m + ( 1 − β 1 ) ⋅ ∇ J ( w ) m = \beta_1 \cdot m + (1 - \beta_1) \cdot \nabla J(w) m=β1⋅m+(1−β1)⋅∇J(w)
v = β 2 ⋅ v + ( 1 − β 2 ) ⋅ ( ∇ J ( w ) ) 2 v = \beta_2 \cdot v + (1 - \beta_2) \cdot (\nabla J(w))^2 v=β2⋅v+(1−β2)⋅(∇J(w))2
m ^ = m 1 − β 1 t \hat{m} = \frac{m}{1 - \beta_1^t} m^=1−β1tm
v ^ = v 1 − β 2 t \hat{v} = \frac{v}{1 - \beta_2^t} v^=1−β2tv
w = w − α v ^ + ϵ ⋅ m ^ w = w - \frac{\alpha}{\sqrt{\hat{v} + \epsilon}} \cdot \hat{m} w=w−v^+ϵα⋅m^
其中, m m m 和 v v v 分别是动量和平方梯度的移动平均, β 1 \beta_1 β1 和 β 2 \beta_2 β2 是衰减系数, t t t 是当前迭代次数, ϵ \epsilon ϵ 是避免除零错误的小数。
其实,每种优化器都有其适用的场景,具体的选择需要根据问题的特性和实际实验的结果来决定。
如果你真的对优化器的数学原理不感冒,只是一个最小白的神经网络构建者,那么我尝试总结几条,最浅显易懂的优化器特征,以供查阅:
-
随机梯度下降(SGD):这是最基本的优化算法之一,它在每个训练步骤中沿着梯度的反方向更新权重。它有时候可能需要更多的调参工作来获得好的性能。
-
动量优化器(Momentum):当需要考虑前一次梯度调整对后续修正的影响时,这个方法不错。Momentum 的参数 momentum 控制了之前梯度的影响程度,一般取值在 0.8 到 0.9 之间。
-
Adagrad:Adagrad 会为不经常更新的参数提供更大的学习率,适合处理稀疏数据。
-
RMSprop:与 Adam 类似,RMSprop 也是自适应学习率的一种算法。在一些情况下,它可能会比 Adam 更好。
-
Adam:Adam 通过自适应调整学习率来提高训练效率。它通常对于大多数问题都是一个良好的默认选择。
-
Adadelta:Adadelta 是一种自适应学习率的优化器,可以自动调整学习率。
-
Nadam:Nadam 是结合了 Nesterov 动量的 Adam 变体,通常在训练深度神经网络时表现良好。
-
FTRL:FTRL 是针对线性模型优化的一种算法,对于大规模线性模型可以很有效。
联系我 交流请署名👇

相关文章:

简单介绍神经网络中不同优化器的数学原理及使用特性【含规律总结】
当涉及到优化器时,我们通常是在解决一个参数优化问题,也就是寻找能够使损失函数最小化的一组参数。当我们在无脑用adam时,有没有斟酌过用这个是否合适,或者说凭经验能够有目的性换用不同的优化器?是否用其他的优化器可…...

JL653—一个基于ARINC653的应用程序仿真调试工具
JL653是安装在PC机Windows操作系统上面的一层接插件,它能够真实地模拟ARINC653标准规定的功能性行为,从而可以供研发人员在PC机Windows环境下高效、快速的进行基于ARINC653的应用程序的开发、调试等。 JL653提供了ARINC 653 Part 1中要求的以下服务&…...
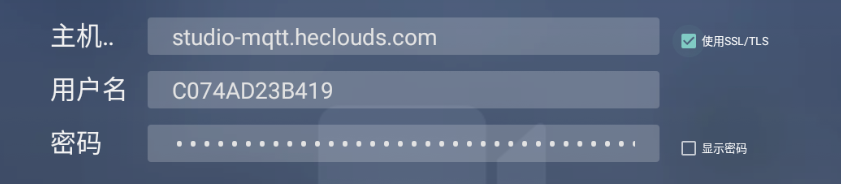
MQTT Paho Android 支持SSL/TLS(亲测有效)
MQTT Paho Android 支持SSL/TLS(亲测有效) 登录时支持ssl的交互 这是调测登录界面设计 代码中对ssl/tls的支持 使用MqttAndroidClient配置mqtt客户端请求时,不加密及加密方式连接存在以下几点差异: url及端口差异 val uri: String if (tlsConnect…...
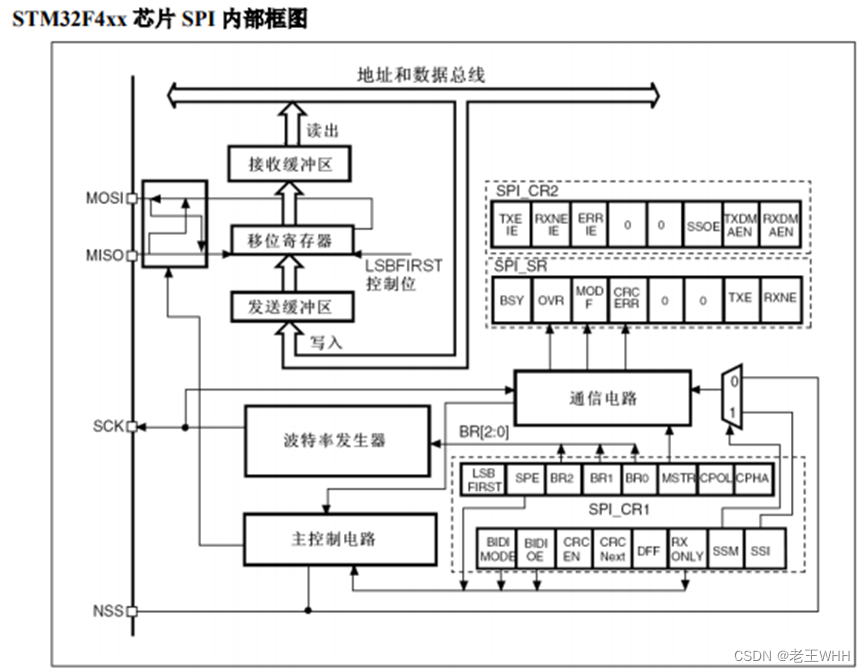
STM32——SPI通信
文章目录 SPI(Serial Peripheral Interface)概述:SPI的硬件连接:SPI的特点和优势:SPI的常见应用:SPI的工作方式和时序图分析:工作模式传输模式与时序分析工作流程 SPI设备的寄存器结构和寄存器设…...

Linux虚拟机局域网IP配置
前言 应用程序包部署在主机(Window)的虚拟机(Linux CentOS7)上,把主机当做一个服务器,在局域网中访问部署在主机上的应用程序,配置Linux网络。 文章如有侵权,无意为之,…...

MacOS删除.DS_Store文件
目录 .DS_Store是什么删除命令防止再生命令 .DS_Store是什么 在 Mac OS X 系统下,几乎绝大部分文件夹中都包含 .DS_Store 隐藏文件,这里保存着针对这个目录的特殊信息和设置配置,例如查看方式、图标大小以及这个目录的一些附属元数据。 而在…...
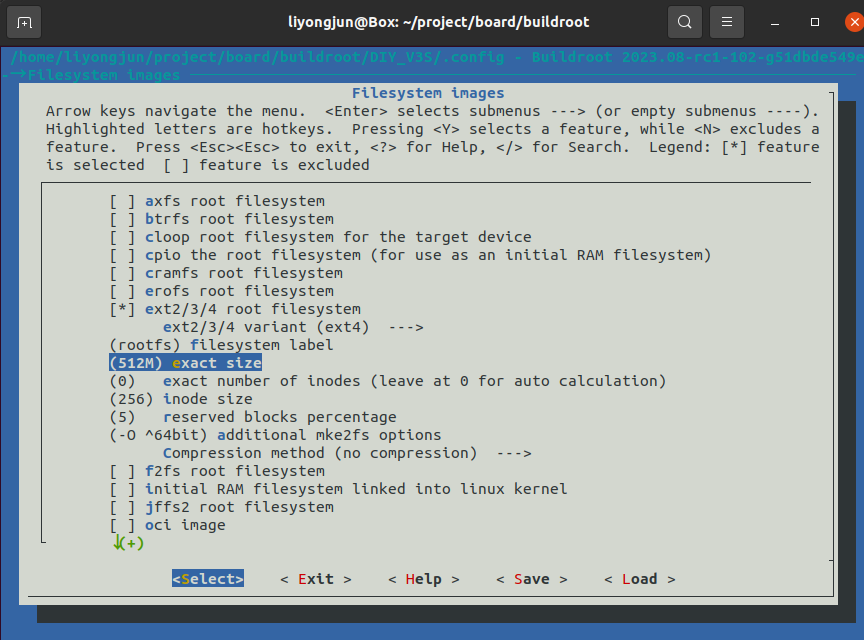
ARM Linux DIY(十一)板子名称、开机 logo、LCD 控制台、console 免登录、命令提示符、文件系统大小
文章目录 前言板子名称uboot Modelkernel 欢迎词、主机名 开机 logoLCD 控制台console 免登录命令提示符文件系统大小 前言 经过前面十篇文章的介绍,硬件部分调试基本完毕,接下来的文章开始介绍软件的个性化开发。 板子名称 uboot Model 既然是自己的…...

【Unity程序技巧】Unity中的单例模式的运用
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:Uni…...
最长连续数列,移动零)
java leetcodetop100 (3,4 )最长连续数列,移动零
top3 最长连续数列 给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。 * * 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 * * * * 示例 1: * * 输入:nums [100,…...
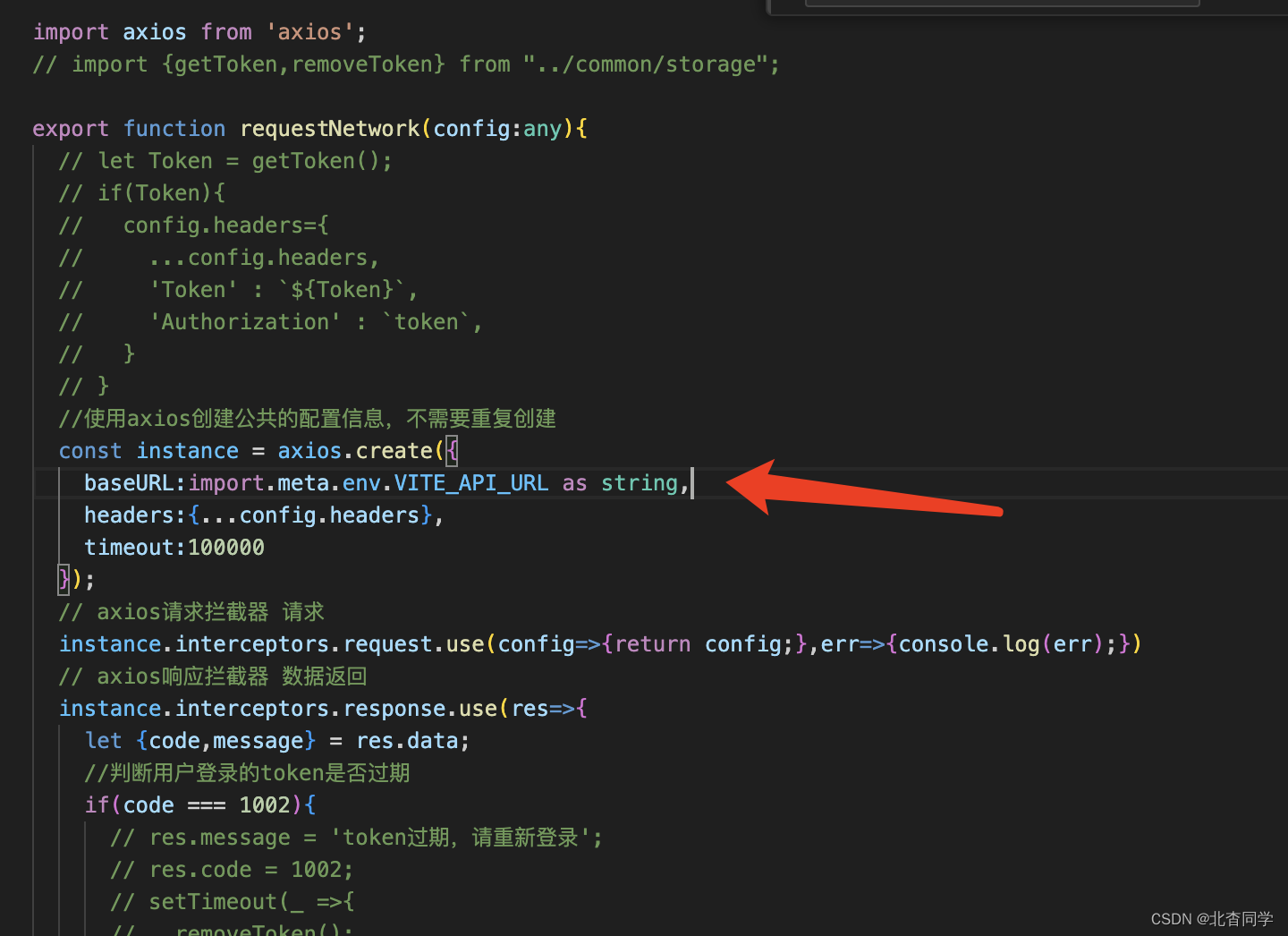
用Vite从零到一创建React+ts项目
方式一:使用create-react-app命令创建项目 1、使用以下命令初始化一个空的npm 项目 npm init -y 2、输入以下命令安装React npm i create-react-app ps:如果失败的话尝试(1:使用管理员身份执行命令(2:切换镜像重…...
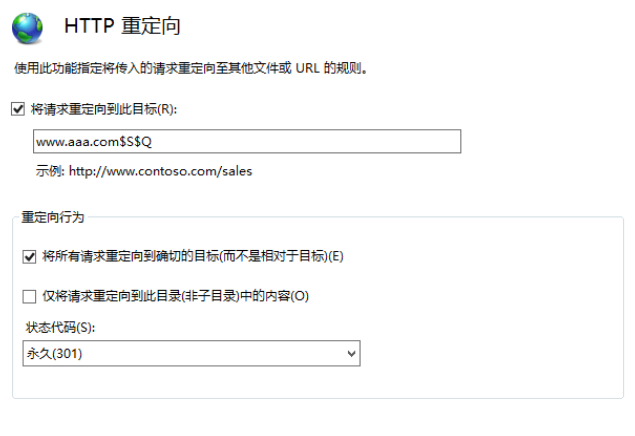
HTTP状态码301(永久重定向)不同Web服务器的配置方法
文章目录 301状态码通常在那些情况下使用301永久重定向配置Nginx配置301永久重定向Windows配置IIS301永久重定向PHP下的301重定向Apache服务器实现301重定向 301重定向是否违反相关法规?推荐阅读 当用户或搜索引擎向服务器发出浏览请求时,服务器返回的HT…...
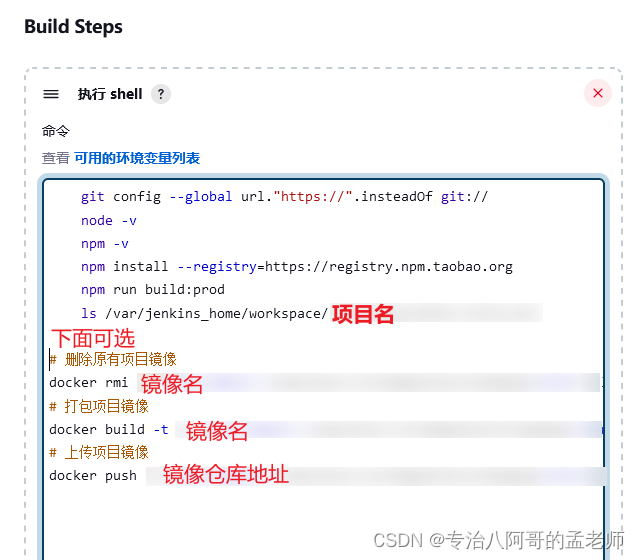
vue-element-admin项目部署 nginx动态代理 含Docker部署、 Jenkins构建
介绍三种方式: 1.直接部署到nginx中 2.用nginx docker镜像部署 3.使用Jenkins构建 1.直接用nginx部署 vue-element-admin项目下有两个.env文件,.env.production是生产环境的,.env.developpment是开发环境的 vue-element-admin默认用的是mock数…...
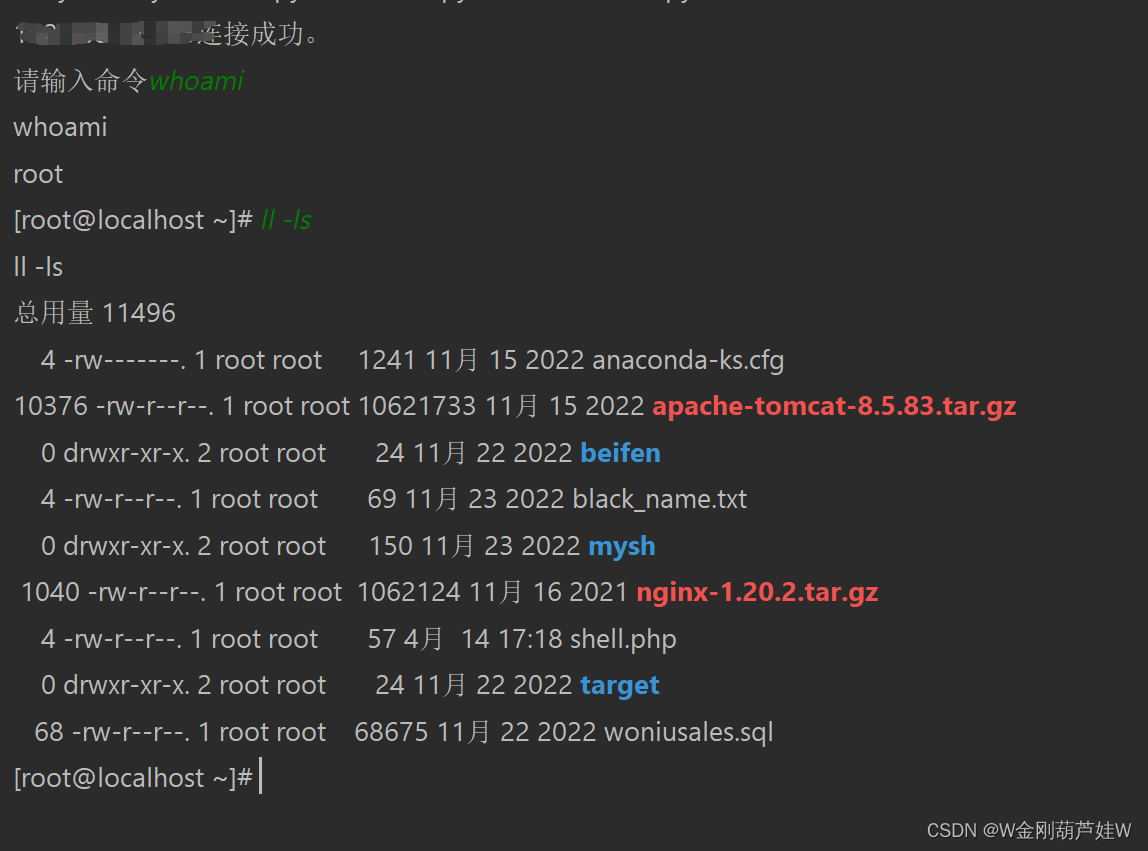
使用Python来写模拟Xshell实现远程命令执行与交互
一、模块 这里使用的是 paramiko带三方库 pip install paramiko二、效果图 三、代码实现(这里的IP,用户名,密码修改为自己对应服务器的) import paramiko import timeclass Linux(object):# 参数初始化def __init__(self, ip, us…...

mybatis 数据库字段为空or为空串 忽略条件过滤, 不为空且不为空串时才需nameParam过滤条件
name未配置视为不考虑name条件 select * from user where (( (ISNULL(name)) OR (name) ) OR name #{user.nameParam} ) 三个or语句 推荐这个 select * from user where ISNULL(name) OR name OR name #{user.nameParam} select * from user where ISNULL(name) OR …...
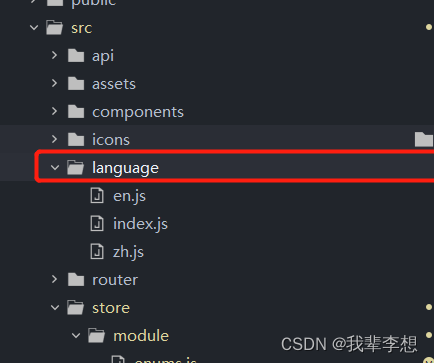
【玩玩Vue】通过vue-store实现枚举管理,用于下拉选项和中英文翻译等
原文作者:我辈李想 版权声明:文章原创,转载时请务必加上原文超链接、作者信息和本声明。 文章目录 一、store基础用法1.在src下新建store文件夹,在store下新建module文件夹2.在module下新建enums.js文件3.在store下新建getters.js…...

ISCSI:后端卷以LVM 的方式配置 ISCSI 目标启动器
写在前面 准备考试整理相关笔记博文内容涉及使用 LVM 做ISCSI 目标后端块存储 Demo理解不足小伙伴帮忙指正 对每个人而言,真正的职责只有一个:找到自我。然后在心中坚守其一生,全心全意,永不停息。所有其它的路都是不完整的&#…...

八公山豆腐发展现状与销售对策研究
1.引言 八公山豆腐作为中国传统特色食品之一,一直以来备受人们的喜爱。然而,在现代社会中,由于消费者对于营养健康的追求以及市场竞争的加剧,八公山豆腐的市场份额逐渐缩小。因此,为了更好地推广和发展八公山豆腐&…...

排序算法-插入排序
属性 当插入第i(i>1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移 直接插入排序…...
数码管显示)
多位数按键操作(闪烁)数码管显示
/*----------------------------------------------- 内容:按键加减数字,多个数码管显示 ------------------------------------------------*/ #include<reg52.h> //包含头文件,一般情况不需要改动,头文件包含特殊功能寄存…...

MyEclipse项目导入与导出
一、项目导出 1、右键选择项目名称,弹出菜单中选择“export”,如下图所示 2、选择“恶心“export”,弹出菜单如下;在“General“选项中,选择“File System”选项 3、点击“next”,进入保存位置选择界面&am…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
