机器学习笔记之最优化理论与算法(十二)无约束优化问题——共轭梯度法
机器学习笔记之最优化理论与方法——共轭梯度法
- 引言
- 回顾:共轭方向法的重要特征
- 线性共轭梯度法
- 共轭方向公式的证明过程
- 关于线搜索公式中参数的化简
- 关于线搜索公式中步长部分的化简
- 关于线搜索公式中共轭方向系数的化简
- 参数化简的目的
- 非线性共轭梯度法(FR,PRP方法)
- 关于非线性共轭梯度法的说明
引言
上一节主要介绍了共轭方向法的重要特征以及相关证明,本节将介绍共轭方向法的代表算法——共轭梯度法。
回顾:共轭方向法的重要特征
关于凸二次函数 f ( x ) f(x) f(x)的优化问题: min f ( x ) = 1 2 x T Q x + C T x \begin{aligned}\min f(x) = \frac{1}{2}x^T \mathcal Qx + \mathcal C^T x \end{aligned} minf(x)=21xTQx+CTx,给定初始点 x 0 x_0 x0以及关于正交矩阵 Q \mathcal Q Q的一系列共轭方向: D = { d 0 , d 1 , ⋯ , d n − 1 } \mathcal D = \{d_0,d_1,\cdots,d_{n-1}\} D={d0,d1,⋯,dn−1},在迭代过程中的输出位置 x k ( k = 1 , 2 , ⋯ , n ) x_k(k=1,2,\cdots,n) xk(k=1,2,⋯,n)表示如下:
x k = x k − 1 + α k − 1 ⋅ d k − 1 k = 1 , 2 , ⋯ , n x_k = x_{k-1} + \alpha_{k-1} \cdot d_{k-1} \quad k = 1,2,\cdots,n xk=xk−1+αk−1⋅dk−1k=1,2,⋯,n
基于上述操作产生的数值解序列 { x k } k = 1 n \{x_k\}_{k=1}^n {xk}k=1n具有如下特征:
- 目标函数 f ( ⋅ ) f(\cdot) f(⋅)在输出位置 x k x_k xk处的梯度 ∇ f ( x k ) \nabla f(x_k) ∇f(xk)与迭代过程中使用过的共轭方向 d i ( i = 0 , 1 , ⋯ , k − 1 ) d_i(i=0,1,\cdots,k-1) di(i=0,1,⋯,k−1)均相互垂直:
[ ∇ f ( x k ) ] T d i = 0 i = 0 , 1 , ⋯ , k − 1 [\nabla f(x_k)]^T d_i = 0 \quad i=0,1,\cdots,k-1 [∇f(xk)]Tdi=0i=0,1,⋯,k−1 - 如果定义集合 X k \mathcal X_k Xk为 k k k次迭代过程中 x k x_k xk可选择的位置空间:
X k = { x 0 + ∑ i = 0 k − 1 α i ⋅ d i ∣ α i ∈ R } \mathcal X_k = \left\{x_0 + \sum_{i=0}^{k-1} \alpha_i \cdot d_i \mid \alpha_i \in \mathbb R\right\} Xk={x0+i=0∑k−1αi⋅di∣αi∈R}
那么如果 x k x_k xk是第 k k k次迭代的最优解,等价于:
x k = arg min x { 1 2 x T Q x + C T x ∣ x ∈ X k } x_k = \mathop{\arg\min}\limits_{x} \left\{\frac{1}{2} x^T \mathcal Q x + \mathcal C^T x \mid x \in \mathcal X_k \right\} xk=xargmin{21xTQx+CTx∣x∈Xk}
并且当 k = n k=n k=n时,此时的位置空间 X n \mathcal X_n Xn就是由共轭方向 d 0 , d 1 , ⋯ , d n − 1 d_0,d_1,\cdots,d_{n-1} d0,d1,⋯,dn−1描述的投影空间: X n ∈ R n \mathcal X_n \in \mathbb R^n Xn∈Rn,因而目标函数 f ( x ) f(x) f(x)必然可以通过最多 n n n次迭代找到最优解。首先,投影空间与原始特征空间不同,它是将正定矩阵 Q \mathcal Q Q对角化后的特征空间效果;该特征空间是由共轭方向 d i ( i = 0 , 1 , ⋯ , n − 1 ) d_i(i=0,1,\cdots,n-1) di(i=0,1,⋯,n−1)但并不是说它们是正交基:
∀ d i , d j ∈ D , i ≠ j ⇒ ( d i ) T Q d j = 0 \forall d_i,d_j \in \mathcal D,i \neq j \Rightarrow (d_i)^T \mathcal Q d_j = 0 ∀di,dj∈D,i=j⇒(di)TQdj=0
令 Q = P 2 = P T P \mathcal Q = \mathcal P^2 = \mathcal P^T \mathcal P Q=P2=PTP,其中 P \mathcal P P同样是正定矩阵。有:
( d i ) T Q d j = ( d i ) T P T P d j = ( P d i ) T ( P d j ) = 0 \begin{aligned} (d_i)^T \mathcal Q d_j & = (d_i)^T \mathcal P^T \mathcal P d_j \\ & = (\mathcal P d_i)^T (\mathcal P d_j) = 0 \end{aligned} (di)TQdj=(di)TPTPdj=(Pdi)T(Pdj)=0
可以看出: P d i ( i = 0 , 1 , ⋯ , n − 1 ) \mathcal P d_i(i=0,1,\cdots,n-1) Pdi(i=0,1,⋯,n−1)才是投影空间的正交基。当然 d i d_i di也有成为正交基的情况,即: Q = P 2 = P ⇒ P = I \mathcal Q = \mathcal P^2 = \mathcal P \Rightarrow \mathcal P = \mathcal I Q=P2=P⇒P=I。其中 I \mathcal I I表示单位矩阵。
线性共轭梯度法
显然,上面存在被我们忽视的核心问题:如何通过一种简单方式获取一组共轭方向 ? ? ?
而共轭梯度法构造共轭方向的思想在于:在迭代下降的过程中,借助当前位置 x k x_k xk的梯度信息构造共轭方向。对应算法步骤表示如下:
该操作是在迭代过程的同时构造梯度方向:初始化 d 0 d_0 d0,在构造新的共轭方向 d 1 d_1 d1时,需要保证其与 d 0 d_0 d0共轭;在构造 d 2 d_2 d2时,需要保证其与 d 0 , d 1 d_0,d_1 d0,d1均相互共轭,以此类推。
初始化操作:
- 给定初始点 x 0 x_0 x0,记 d 0 = − ∇ f ( x 0 ) d_0 = -\nabla f(x_0) d0=−∇f(x0);设置阈值 ϵ > 0 \epsilon > 0 ϵ>0; k = 0 k = 0 k=0
算法过程:
- 事先判断 ∥ ∇ f ( x k ) ∥ ≤ ϵ \|\nabla f(x_k)\| \leq \epsilon ∥∇f(xk)∥≤ϵ是否成立 ? ? ?是,则算法终止;
- 计算当前迭代步骤的最优步长 α k \alpha_k αk:
求解过程详见共轭梯度法背景介绍
α k = − [ ∇ f ( x k ) ] T d k ( d k ) T Q d k \alpha_k = - \frac{[\nabla f(x_k)]^T d_k}{(d_k)^T \mathcal Q d_k} αk=−(dk)TQdk[∇f(xk)]Tdk - 计算新位置点: x k + 1 = x k + α k ⋅ d k x_{k+1} = x_k + \alpha_k \cdot d_k xk+1=xk+αk⋅dk,并计算共轭方向 d k + 1 d_{k+1} dk+1:
d k + 1 = − ∇ f ( x k + 1 ) + β k ⋅ d k , β k = [ ∇ f ( x k + 1 ) ] T Q d k ( d k ) T Q d k d_{k+1} = -\nabla f(x_{k+1}) + \beta_k \cdot d_k,\beta_k = \frac{[\nabla f(x_{k+1})]^T \mathcal Q d_k}{(d_k)^T \mathcal Q d_k} dk+1=−∇f(xk+1)+βk⋅dk,βk=(dk)TQdk[∇f(xk+1)]TQdk - 令 k = k + 1 k = k + 1 k=k+1,转步骤 1 1 1重新判断。
共轭方向公式的证明过程
新共轭方向产生时,需要满足一个重要条件:与之前迭代产生的共轭方向均共轭:
( d k + 1 ) T Q d i = 0 i = 0 , 1 , 2 , ⋯ , k (d_{k+1})^T \mathcal Q d_{i} = 0 \quad i=0,1,2,\cdots,k (dk+1)TQdi=0i=0,1,2,⋯,k
首先,尝试将 d k + 1 d_{k+1} dk+1表示为: x k + 1 x_{k+1} xk+1负梯度方向 − ∇ f ( x k + 1 ) - \nabla f(x_{k+1}) −∇f(xk+1)与 d 0 , d 1 , ⋯ , d k d_0,d_1,\cdots,d_k d0,d1,⋯,dk线性组合的加法形式:
其中 β 0 , ⋯ , β k \beta_0,\cdots,\beta_k β0,⋯,βk表示对应共轭方向的系数,是一个标量;
d k + 1 = − ∇ f ( x k + 1 ) + β 0 d 0 + β 1 d 1 ⋯ + β k d k d_{k+1} = - \nabla f(x_{k+1}) + \beta_0 d_0 + \beta_1d_1 \cdots + \beta_k d_k dk+1=−∇f(xk+1)+β0d0+β1d1⋯+βkdk
将该式代入上面的重要条件,即:
在线性组合中,除去与 d i d_i di相同的一项外,其余项均为 0 0 0。
( d k + 1 ) T Q d i = 0 ⇒ [ − ∇ f ( x k + 1 ) + β 0 d 0 + β 1 d 1 ⋯ + β k d k ] T Q d i = 0 ⇒ [ − ∇ f ( x k + 1 ) ] T Q d i + β 0 ⋅ ( d 0 ) T Q d i ⏟ = 0 + ⋯ + β i ⋅ ( d i ) T Q d i + ⋯ + β k ( d k ) T Q d i ⏟ = 0 = 0 ⇒ [ − ∇ f ( x k + 1 ) ] T Q d i + β i ⋅ ( d i ) T Q d i = 0 \begin{aligned} (d_{k+1})^T \mathcal Q d_{i} = 0 & \Rightarrow [-\nabla f(x_{k+1}) + \beta_0 d_0 + \beta_1d_1 \cdots + \beta_k d_k]^T \mathcal Q d_i = 0 \\ & \Rightarrow [- \nabla f(x_{k+1})]^T\mathcal Q d_i + \beta_0 \cdot \underbrace{(d_0)^T \mathcal Q d_i}_{=0} + \cdots + \beta_i \cdot (d_i)^T \mathcal Q d_i + \cdots + \beta_k \underbrace{(d_k)^T \mathcal Q d_i}_{=0} = 0 \\ & \Rightarrow [- \nabla f(x_{k+1})]^T\mathcal Q d_i + \beta_i \cdot (d_i)^T \mathcal Q d_i = 0 \end{aligned} (dk+1)TQdi=0⇒[−∇f(xk+1)+β0d0+β1d1⋯+βkdk]TQdi=0⇒[−∇f(xk+1)]TQdi+β0⋅=0 (d0)TQdi+⋯+βi⋅(di)TQdi+⋯+βk=0 (dk)TQdi=0⇒[−∇f(xk+1)]TQdi+βi⋅(di)TQdi=0
经过整理,有:
很明显:项 ( d i ) T Q d i (d_i)^T \mathcal Q d_i (di)TQdi与项 [ ∇ f ( x k + 1 ) ] T Q d i [\nabla f(x_{k+1})]^T \mathcal Q d_i [∇f(xk+1)]TQdi描述的都是 1 × 1 1 \times 1 1×1的矩阵,一个值,移项就好啦~
β i ⋅ ( d i ) T Q d i = ∇ f ( x k + 1 ) T Q d i ⇒ β i = [ ∇ f ( x k + 1 ) ] T Q d i ( d i ) T Q d i \beta_i \cdot (d_i)^T \mathcal Q d_i = \nabla f(x_{k+1})^T \mathcal Q d_i \Rightarrow \beta_i = \frac{[\nabla f(x_{k+1})]^T \mathcal Q d_i}{(d_i)^T \mathcal Q d_i} βi⋅(di)TQdi=∇f(xk+1)TQdi⇒βi=(di)TQdi[∇f(xk+1)]TQdi
此时,当 β i \beta_i βi确定后, d k + 1 d_{k+1} dk+1必然与 d i d_i di共轭。同理,可以对所有的 β i ( i = 0 , 1 , ⋯ , k ) \beta_i(i=0,1,\cdots,k) βi(i=0,1,⋯,k)进行求解,当所有的 β \beta β值确定后,必然与 d 0 , d 1 , ⋯ , d k d_0,d_1,\cdots,d_k d0,d1,⋯,dk均共轭。但上面的结论公式中,仅仅描述了 β k \beta_k βk参数。也就是说:在迭代公式中,仅描述了 d k + 1 d_{k+1} dk+1与 d k d_k dk共轭,其余的共轭方向并没有提。
观察除了 d k d_k dk之外的其他项。当 j = 0 , 1 , ⋯ , k − 1 j=0,1,\cdots,k-1 j=0,1,⋯,k−1时,观察 β j \beta_j βj的分子部分:
[ ∇ f ( x k + 1 ) ] T Q d j [\nabla f(x_{k+1})]^T \mathcal Q d_j [∇f(xk+1)]TQdj
关于共轭方向 d j d_j dj,通过线搜索公式可以将其表示为如下形式:
x j + 1 = x j + α j ⋅ d j ⇒ d j = x j + 1 − x j α j x_{j+1} = x_j + \alpha_j \cdot d_j \Rightarrow d_j = \frac{x_{j+1} - x_j}{\alpha_j} xj+1=xj+αj⋅dj⇒dj=αjxj+1−xj
两边同时左乘正定矩阵 Q \mathcal Q Q,有:
在小括号内两项同时加上系数项 C \mathcal C C,符号不发生变化。很明显, Q x j + 1 + C \mathcal Q x_{j+1} + \mathcal C Qxj+1+C就是 ∇ f ( x j + 1 ) , ∇ f ( x j ) \nabla f(x_{j+1}),\nabla f(x_j) ∇f(xj+1),∇f(xj)同理。
Q d j = 1 α j ( Q x j + 1 − Q x j ) = 1 α j [ ( Q x j + 1 + C ) − ( Q x j + C ) ] = 1 α j [ ∇ f ( x j + 1 ) − ∇ f ( x j ) ] \begin{aligned} \mathcal Q d_j & = \frac{1}{\alpha_j}(\mathcal Q x_{j+1} - \mathcal Q x_j) \\ & = \frac{1}{\alpha_j} \left[(\mathcal Q x_{j+1} + \mathcal C) - (\mathcal Q x_j + \mathcal C) \right] \\ & = \frac{1}{\alpha_j} [\nabla f(x_{j+1}) - \nabla f(x_j)] \end{aligned} Qdj=αj1(Qxj+1−Qxj)=αj1[(Qxj+1+C)−(Qxj+C)]=αj1[∇f(xj+1)−∇f(xj)]
将 Q d j \mathcal Q d_j Qdj的展开结果代入上式,有:
[ ∇ f ( x k + 1 ) ] T Q d j = 1 α j ⋅ [ ∇ f ( x k + 1 ) ] T [ ∇ f ( x j + 1 ) − ∇ f ( x j ) ] = 1 α j ⋅ { [ ∇ f ( x k + 1 ) ] T ∇ f ( x j + 1 ) − [ ∇ f ( x k + 1 ) ] T ∇ f ( x j ) } \begin{aligned} [\nabla f(x_{k+1})]^T \mathcal Q d_j & = \frac{1}{\alpha_j} \cdot [\nabla f(x_{k+1})]^T [\nabla f(x_{j+1}) - \nabla f(x_j)] \\ & = \frac{1}{\alpha_j} \cdot \left\{[\nabla f(x_{k+1})]^T \nabla f(x_{j+1}) - [\nabla f(x_{k+1})]^T\nabla f(x_j)\right\} \end{aligned} [∇f(xk+1)]TQdj=αj1⋅[∇f(xk+1)]T[∇f(xj+1)−∇f(xj)]=αj1⋅{[∇f(xk+1)]T∇f(xj+1)−[∇f(xk+1)]T∇f(xj)}
观察大括号内第一项: [ ∇ f ( x k + 1 ) ] T ∇ f ( x j + 1 ) [\nabla f(x_{k+1})]^T \nabla f(x_{j+1}) [∇f(xk+1)]T∇f(xj+1),将 ∇ f ( x j + 1 ) \nabla f(x_{j+1}) ∇f(xj+1)使用共轭方向进行表示:
d j + 1 = − ∇ f ( x j + 1 ) + β 0 d 0 + β 1 d 1 + ⋯ β j d j ⇓ ∇ f ( x j + 1 ) = − d j + 1 + β 0 d 0 + β 1 d 1 + ⋯ + β j d j d_{j+1} = -\nabla f(x_{j+1}) + \beta_0 d_0 + \beta_1 d_1 + \cdots \beta_j d_j \\ \Downarrow \\ \nabla f(x_{j+1}) = -d_{j+1} + \beta_0 d_0 + \beta_1 d_1 + \cdots + \beta_j d_j dj+1=−∇f(xj+1)+β0d0+β1d1+⋯βjdj⇓∇f(xj+1)=−dj+1+β0d0+β1d1+⋯+βjdj
将其代入,有:
根据共轭方向法的第一条重要特征,所有项全部是 0 0 0。
[ ∇ f ( x k + 1 ) ] T ∇ f ( x j + 1 ) = − [ ∇ f ( x k + 1 ) ] T d j + 1 ⏟ = 0 + β 0 ⋅ [ ∇ f ( x k + 1 ) ] T d 0 ⏟ = 0 + ⋯ + β j ⋅ [ ∇ f ( x k + 1 ) ] T d j ⏟ = 0 = 0 \begin{aligned} [\nabla f(x_{k+1})]^T \nabla f(x_{j+1}) & = - \underbrace{[\nabla f(x_{k+1})]^Td_{j+1}}_{=0} + \beta_0 \cdot\underbrace{[\nabla f(x_{k+1})]^T d_0}_{=0} + \cdots + \beta_j \cdot \underbrace{[\nabla f(x_{k+1})]^T d_j}_{=0} \\ & = 0 \end{aligned} [∇f(xk+1)]T∇f(xj+1)=−=0 [∇f(xk+1)]Tdj+1+β0⋅=0 [∇f(xk+1)]Td0+⋯+βj⋅=0 [∇f(xk+1)]Tdj=0
同理,大括号内第二项: [ ∇ f ( x k + 1 ) ] T ∇ f ( x j ) = 0 [\nabla f(x_{k+1})]^T\nabla f(x_j) = 0 [∇f(xk+1)]T∇f(xj)=0。最终可得:当 j = 0 , 1 , ⋯ , k − 1 j=0,1,\cdots,k-1 j=0,1,⋯,k−1时,对应的分子 β j = 0 \beta_j = 0 βj=0,最终整理,有:
d k + 1 = − ∇ f ( x k + 1 ) + β k ⋅ d k , β k = [ ∇ f ( x k + 1 ) ] T Q d k ( d k ) T Q d k d_{k+1} = -\nabla f(x_{k+1}) + \beta_k \cdot d_k,\beta_k = \frac{[\nabla f(x_{k+1})]^T \mathcal Q d_k}{(d_k)^T \mathcal Q d_k} dk+1=−∇f(xk+1)+βk⋅dk,βk=(dk)TQdk[∇f(xk+1)]TQdk
关于线搜索公式中参数的化简
关于线搜索公式中步长部分的化简
关于精确搜索条件下步长 α k = − [ ∇ f ( x k ) ] T d k ( d k ) T Q d k \begin{aligned}\alpha_k = -\frac{[\nabla f(x_k)]^T d_k}{(d_k)^T \mathcal Q d_k}\end{aligned} αk=−(dk)TQdk[∇f(xk)]Tdk,可以将其化简为如下形式:
目的是为了将线搜索过程中变量 α k , d k \alpha_k,d_k αk,dk的表达式与目标函数梯度信息建立起直观联系。
α k = [ ∇ f ( x k ) ] T ∇ f ( x k ) ( d k ) T Q d k \alpha_k = \frac{[\nabla f(x_k)]^T \nabla f(x_k)}{(d_k)^T \mathcal Q d_k} αk=(dk)TQdk[∇f(xk)]T∇f(xk)
化简描述:观察 α k \alpha_k αk分子部分的描述: [ ∇ f ( x k ) ] T d k [\nabla f(x_k)]^T d_k [∇f(xk)]Tdk,由于共轭方向 d k d_k dk可表示为:
d k = − ∇ f ( x k ) + β k − 1 ⋅ d k − 1 d_k = - \nabla f(x_{k}) + \beta_{k-1} \cdot d_{k-1} dk=−∇f(xk)+βk−1⋅dk−1
对分子进行整理:
依然使用第一条重要特征: [ ∇ f ( x k ) ] T d k − 1 = 0 [\nabla f(x_k)]^Td_{k-1} = 0 [∇f(xk)]Tdk−1=0
[ ∇ f ( x k ) ] T d k = [ ∇ f ( x k ) ] T [ − ∇ f ( x k ) + β k − 1 ⋅ d k − 1 ] = − [ ∇ f ( x k ) ] T ∇ f ( x k ) + β k − 1 ⋅ [ ∇ f ( x k ) ] T d k − 1 ⏟ 0 = − [ ∇ f ( x k ) ] T ∇ f ( x k ) \begin{aligned} [\nabla f(x_k)]^T d_k & = [\nabla f(x_k)]^T [-\nabla f(x_k) + \beta_{k-1} \cdot d_{k-1}] \\ & = -[\nabla f(x_k)]^T \nabla f(x_k) + \beta_{k-1}\cdot \underbrace{[\nabla f(x_k)]^Td_{k-1}}_{0} \\ & = -[\nabla f(x_k)]^T \nabla f(x_k) \end{aligned} [∇f(xk)]Tdk=[∇f(xk)]T[−∇f(xk)+βk−1⋅dk−1]=−[∇f(xk)]T∇f(xk)+βk−1⋅0 [∇f(xk)]Tdk−1=−[∇f(xk)]T∇f(xk)
最终对分子部分进行替换即可。
关于线搜索公式中共轭方向系数的化简
精确搜索条件下关于共轭方向系数 β k = ∇ f ( x k + 1 ) Q d k ( d k ) T Q d k \begin{aligned}\beta_k = \frac{\nabla f(x_{k+1}) \mathcal Q d_k}{(d_k)^T \mathcal Q d_k}\end{aligned} βk=(dk)TQdk∇f(xk+1)Qdk,可以将其化简为如下形式:
β k = [ ∇ f ( x k + 1 ) ] T ∇ f ( x k + 1 ) [ ∇ f ( x k ) ] T ∇ f ( x k ) \beta_k = \frac{[\nabla f(x_{k+1})]^T\nabla f(x_{k+1})}{[\nabla f(x_k)]^T \nabla f(x_k)} βk=[∇f(xk)]T∇f(xk)[∇f(xk+1)]T∇f(xk+1)
化简描述:观察分子 [ ∇ f ( x k + 1 ) ] T Q d k [\nabla f(x_{k+1})]^T\mathcal Q d_k [∇f(xk+1)]TQdk,使用 Q d k = 1 α k [ ∇ f ( x k + 1 ) − ∇ f ( x k ) ] \begin{aligned}\mathcal Qd_k = \frac{1}{\alpha_k}[\nabla f(x_{k+1}) - \nabla f(x_k)]\end{aligned} Qdk=αk1[∇f(xk+1)−∇f(xk)]进行替换,对于 β k \beta_k βk有如下表达:
β k = 1 α k ⋅ [ ∇ f ( x k + 1 ) ] T [ ∇ f ( x k + 1 ) − ∇ f ( x k ) ] ( d k ) T Q d k = [ ∇ f ( x k + 1 ) ] T [ ∇ f ( x k + 1 ) − ∇ f ( x k ) ] α k ⋅ ( d k ) T Q d k \begin{aligned} \beta_k & = \frac{1}{\alpha_k} \cdot \frac{[\nabla f(x_{k+1})]^T[\nabla f(x_{k+1}) - \nabla f(x_k)]}{(d_k)^T \mathcal Q d_k} \\ & = \frac{[\nabla f(x_{k+1})]^T[\nabla f(x_{k+1}) - \nabla f(x_k)]}{\alpha_k \cdot (d_k)^T \mathcal Q d_k} \end{aligned} βk=αk1⋅(dk)TQdk[∇f(xk+1)]T[∇f(xk+1)−∇f(xk)]=αk⋅(dk)TQdk[∇f(xk+1)]T[∇f(xk+1)−∇f(xk)]
根据化简后的 α k \alpha_k αk,有:
[ ∇ f ( x k ) ] T ∇ f ( x k ) = α k ⋅ ( d k ) T Q d k [\nabla f(x_k)]^T \nabla f(x_k) = \alpha_k \cdot (d_k)^T \mathcal Q d_k [∇f(xk)]T∇f(xk)=αk⋅(dk)TQdk
替换 β k \beta_k βk分母,有:
并将 [ ∇ f ( x k + 1 ) ] T ∇ f ( x k ) = 0 [\nabla f(x_{k+1})]^T \nabla f(x_k) = 0 [∇f(xk+1)]T∇f(xk)=0带入
β k = [ ∇ f ( x k + 1 ) ] T [ ∇ f ( x k + 1 ) − ∇ f ( x k ) ] [ ∇ f ( x k ) ] T ∇ f ( x k ) = [ ∇ f ( x k + 1 ) ] T ∇ f ( x k + 1 ) [ ∇ f ( x k ) ] T ∇ f ( x k ) \begin{aligned} \beta_k & = \frac{[\nabla f(x_{k+1})]^T[\nabla f(x_{k+1}) - \nabla f(x_k)]}{[\nabla f(x_k)]^T \nabla f(x_k)} \\ \quad \\ & = \frac{[\nabla f(x_{k+1})]^T\nabla f(x_{k+1})}{[\nabla f(x_k)]^T \nabla f(x_k)} \end{aligned} βk=[∇f(xk)]T∇f(xk)[∇f(xk+1)]T[∇f(xk+1)−∇f(xk)]=[∇f(xk)]T∇f(xk)[∇f(xk+1)]T∇f(xk+1)
参数化简的目的
观察参数: β k = [ ∇ f ( x k + 1 ) ] T ∇ f ( x k + 1 ) [ ∇ f ( x k ) ] T ∇ f ( x k ) \begin{aligned}\beta_k=\frac{[\nabla f(x_{k+1})]^T\nabla f(x_{k+1})}{[\nabla f(x_k)]^T \nabla f(x_k)}\end{aligned} βk=[∇f(xk)]T∇f(xk)[∇f(xk+1)]T∇f(xk+1)的化简结果,可以发现:共轭方向 d k d_k dk的迭代结果只与上一迭代步骤的共轭方向 d k d_k dk与 x k , x k + 1 x_k,x_{k+1} xk,xk+1位置的梯度相关。
d k + 1 = − ∇ f ( x k + 1 ) + [ ∇ f ( x k + 1 ) ] T ∇ f ( x k + 1 ) [ ∇ f ( x k ) ] T ∇ f ( x k ) ⋅ d k d_{k+1} = -\nabla f(x_{k+1}) + \frac{[\nabla f(x_{k+1})]^T\nabla f(x_{k+1})}{[\nabla f(x_k)]^T \nabla f(x_k)} \cdot d_k dk+1=−∇f(xk+1)+[∇f(xk)]T∇f(xk)[∇f(xk+1)]T∇f(xk+1)⋅dk
这意味着:关于共轭方向的迭代过程与正定矩阵 Q \mathcal Q Q,描述一次项系数矩阵 C \mathcal C C没有关联关系。从而可以将凸二次函数 f ( x ) f(x) f(x)的优化问题映射到其他复杂目标函数的优化问题中。
虽然上述的化简过程全部是取等操作,但这些取等操作是依赖于 f ( x ) = 1 2 x T Q x + C T x \begin{aligned}f(x) = \frac{1}{2}x^T \mathcal Q x + \mathcal C^Tx\end{aligned} f(x)=21xTQx+CTx条件的基础上。如果是一般性的复杂目标函数:得到的化简结果 β k \beta_k βk可能只是是一个近似解。因为上述化简过程中可能存在:
当然,不仅仅是下面描述的迭代步骤中存在不相等的情况,在替换 [ ∇ f ( x k ) ] T ∇ f ( x k ) = α k ⋅ ( d k ) T Q d k [\nabla f(x_k)]^T \nabla f(x_k) = \alpha_k \cdot (d_k)^T \mathcal Q d_k [∇f(xk)]T∇f(xk)=αk⋅(dk)TQdk时,无论是 FR \text{FR} FR方法还是 PRP \text{PRP} PRP方法,其得到的 β k \beta_k βk都不是精确解。因为 Q \mathcal Q Q是凸二次函数的特有信息,而一般性目标函数可能不存在该信息,或者说 Q \mathcal Q Q存在,但不作主导作用。
[ ∇ f ( x k + 1 ) ] T [ ∇ f ( x k + 1 ) − ∇ f ( x k ) ] [ ∇ f ( x k ) ] T ∇ f ( x k ) ≠ [ ∇ f ( x k + 1 ) ] T ∇ f ( x k + 1 ) [ ∇ f ( x k ) ] T ∇ f ( x k ) \frac{[\nabla f(x_{k+1})]^T[\nabla f(x_{k+1}) - \nabla f(x_k)]}{[\nabla f(x_k)]^T \nabla f(x_k)} \neq \frac{[\nabla f(x_{k+1})]^T\nabla f(x_{k+1})}{[\nabla f(x_k)]^T \nabla f(x_k)} [∇f(xk)]T∇f(xk)[∇f(xk+1)]T[∇f(xk+1)−∇f(xk)]=[∇f(xk)]T∇f(xk)[∇f(xk+1)]T∇f(xk+1)
非线性共轭梯度法(FR,PRP方法)
关于 FR,PRP \text{FR,PRP} FR,PRP方法的区别在于 β k \beta_k βk的迭代方式。关于非线性共轭梯度法的迭代过程表示如下:
初始化操作:
- 给定初始点 x 0 x_0 x0,记 d 0 = − ∇ f ( x 0 ) d_0 = -\nabla f(x_0) d0=−∇f(x0);设置阈值 ϵ > 0 \epsilon > 0 ϵ>0; k = 0 k = 0 k=0
算法过程:
- 事先判断 ∥ ∇ f ( x k ) ∥ ≤ ϵ \|\nabla f(x_k)\| \leq \epsilon ∥∇f(xk)∥≤ϵ是否成立 ? ? ?是,则算法终止;
- 利用线性搜索方式计算步长 α k \alpha_k αk:
此时的目标函数可能已经不是形如f ( x ) = 1 2 x T Q x + C T x \begin{aligned}f(x) = \frac{1}{2} x^T\mathcal Q x + \mathcal C^T x\end{aligned} f(x)=21xTQx+CTx的格式,因而不能使用公式进行求解;甚至此时的目标函数不一定是凸函数,从而求解的最优解可能仅是局部最优解,而不是全局最优解;在迭代过程中并不一定需要求解精确解,我们的目的是让目标函数收敛至最小值详见线搜索方法——步长角度(精确搜索),因此完全可以使用非精确搜索如 Armijo,Wolfe \text{Armijo,Wolfe} Armijo,Wolfe准则等获取优质步长。
- 计算新位置点: x k + 1 = x k + α k ⋅ d k x_{k+1} = x_k + \alpha_k \cdot d_k xk+1=xk+αk⋅dk,并计算共轭方向 d k + 1 d_{k+1} dk+1:
d k + 1 = − ∇ f ( x k + 1 ) + β k d k d_{k+1} = - \nabla f(x_{k+1}) + \beta_k d_k dk+1=−∇f(xk+1)+βkdk
其中 FR \text{FR} FR方法使用的 β k \beta_k βk的计算方式为:
β k = [ ∇ f ( x k + 1 ) ] T ∇ f ( x k + 1 ) [ ∇ f ( x k ) ] T ∇ f ( x k ) ; ( FR ) \beta_k = \frac{[\nabla f(x_{k+1})]^T\nabla f(x_{k+1})}{[\nabla f(x_k)]^T \nabla f(x_k)}; \quad (\text{FR}) βk=[∇f(xk)]T∇f(xk)[∇f(xk+1)]T∇f(xk+1);(FR)
而 PRP \text{PRP} PRP方法使用 β k \beta_k βk的计算方式为:
β k = [ ∇ f ( x k + 1 ) ] T [ ∇ f ( x k + 1 ) − ∇ f ( x k ) ] [ ∇ f ( x k ) ] T ∇ f ( x k ) ; ( PRP ) \beta_k = \frac{[\nabla f(x_{k+1})]^T[\nabla f(x_{k+1}) - \nabla f(x_k)]}{[\nabla f(x_k)]^T \nabla f(x_k)}; \quad (\text{PRP}) βk=[∇f(xk)]T∇f(xk)[∇f(xk+1)]T[∇f(xk+1)−∇f(xk)];(PRP) - 令 k = k + 1 k = k+1 k=k+1并转步骤 1 1 1重新判断。
关于非线性共轭梯度法的说明
-
根据线搜索公式的描述,在迭代过程中关于共轭方向 d k d_k dk的计算需要满足一个大前提: d k d_k dk是下降方向。相反,如果不是下降方向,需要对参数 β k \beta_k βk进行调整。
但这种调整同样存在风险:d k d_k dk与其他方向不是共轭关系。 -
根据线性共轭梯度法的描述,其必然会在最多 n n n次迭代内找到凸二次函数的全局最优解。这意味着:该算法具有二次终止性;
-
在算法实现过程中通常采用 n n n步重启策略,从而该算法的收敛速度可达到 n n n步二阶收敛。
关于n n n步重启策略的描述:在执行n n n次迭代后,此时当前位置点的所有分量均被更新一次。如果在x n x_n xn位置处开始重新计算梯度:d n = − ∇ f ( x n ) d_{n} = - \nabla f(x_n) dn=−∇f(xn)此时和初始化点x 0 x_0 x0的计算方式是相同的。后续迭代与前面的迭代方式均相同。例如:
d n + 1 = − ∇ f ( x n + 1 ) + β n ⋅ d n d_{n+1} = - \nabla f(x_{n+1}) + \beta_{n} \cdot d_{n} dn+1=−∇f(xn+1)+βn⋅dn
和线性共轭梯度法的区别在于:此时由于复杂的目标函数,该算法无法实现n n n步迭代/1 1 1次线搜索过程完成收敛。也就是说:每 n n n次迭代后,迭代结果会在投影空间中描述一个全新的位置。这里的全新是指所有维度均被更新一次的结果。从而可能需要若干个n n n次迭代才能达到最优解。为什么要使用n n n步重启策略:在迭代足够多次数的情况下,初始的一些共轭方向已经不会对当前迭代结果产生太大作用。但如果使用正常的迭代方式。初始共轭方向依然会以线性组合的形式留在当前迭代结果中,从而影响当前迭代的方向。例如关于d n + 1 d_{n+1} dn+1的正常迭代:
d n + 1 = − ∇ f ( x 0 ) + ∑ i = 0 n β i ⋅ d i d_{n+1} = - \nabla f(x_0) + \sum_{i=0}^{n} \beta_i \cdot d_i dn+1=−∇f(x0)+i=0∑nβi⋅di
Reference \text{Reference} Reference:
最优化理论与方法-第七讲-无约束优化问题(三)
相关文章:
无约束优化问题——共轭梯度法)
机器学习笔记之最优化理论与算法(十二)无约束优化问题——共轭梯度法
机器学习笔记之最优化理论与方法——共轭梯度法 引言回顾:共轭方向法的重要特征线性共轭梯度法共轭方向公式的证明过程 关于线搜索公式中参数的化简关于线搜索公式中步长部分的化简关于线搜索公式中共轭方向系数的化简参数化简的目的 非线性共轭梯度法(FR,PRP方法)关…...

JVM中的java同步互斥工具应用演示及设计分析
1.火车站售票系统仿真 某火车站目前正在出售火车票,共有50张票,而它有3个售票窗口同时售票,下面设计了一个程序模拟该火车站售票,通过实现Runnable接口实现(模拟网络延迟)。 伪代码: Ticket类…...

数据治理-数据质量
实现数据质量的前提就是数据本身是可靠和可信的。 导致数据质量低下的因素 组织缺乏对低质量数据影响的理解,缺乏规划、孤岛式系统设计、不一致的开发过程、不完整的文档、缺乏标准或缺乏治理等。 所有组织都会遇到与数据质量有关的问题。数据质量需要跨职能的承诺…...

[sqoop]hive3.1.2 hadoop3.1.1安装sqoop1.4.7
参考: Hadoop3.2.4Hive3.1.2sqoop1.4.7安装部署_hadoop sqoop安装_alicely07的博客-CSDN博客 一、安装 1、解压 tar -zxvf sqoop-1.4.7.bin__hadoop-2.6.0.tar.gz -C /home/data_warehouse/module mv sqoop-1.4.7.bin__hadoop-2.6.0 sqoop-1.4.72、配置文件 sqoop-env.s…...

js事件的详细介绍
11.事件 1.什么是事件 js属于事件驱动编程,把驱动,执行,调用通过一些交互,触发一些函数事件:发起-->执行绑定事件-->触发事件on 绑定 emit触发 off解绑2.事件分类 鼠标事件 点击事件 onclick 双击事件 ondblclick 按下事件 onmousedown 抬起事件 onmouseup 鼠标进…...
虚幻4学习笔记(12)操控导入的角色、动画蓝图、播放蒙太奇和打包、角色重定向
虚幻4学习笔记 操控导入的角色设置鼠标旋转关掉动态模糊 动画蓝图、播放蒙太奇和打包角色走路奔跑动画shift 奔跑F 跳舞移动打断 跳舞 打包角色重定向姿势调整解决跑步 腿分太开隐藏剑 B站UP谌嘉诚课程:https://www.bilibili.com/video/BV164411Y732 操控导入的角色…...

hive with tez:无法从链中的任何提供者加载aws凭据
环境信息 hadoop 3.1.0 hive-3.1.3 tez 0.9.1 问题描述 可以从hadoop命令行正确地访问s3a uri。我可以创建外部表和如下命令: create external table mytable(a string, b string) location s3a://mybucket/myfolder/; select * from mytable limit 20; 执行正…...
Ubuntu修改静态IP、网关和DNS的方法总结
Ubuntu修改静态IP、网关和DNS的方法总结 ubuntu系统(其他debian的衍生版本好像也可以)修改静态IP有以下几种方法。(搜索总结,可能也不太对) /etc/netplan (use) Ubuntu 18.04开始可以使用netplan配置网络࿰…...
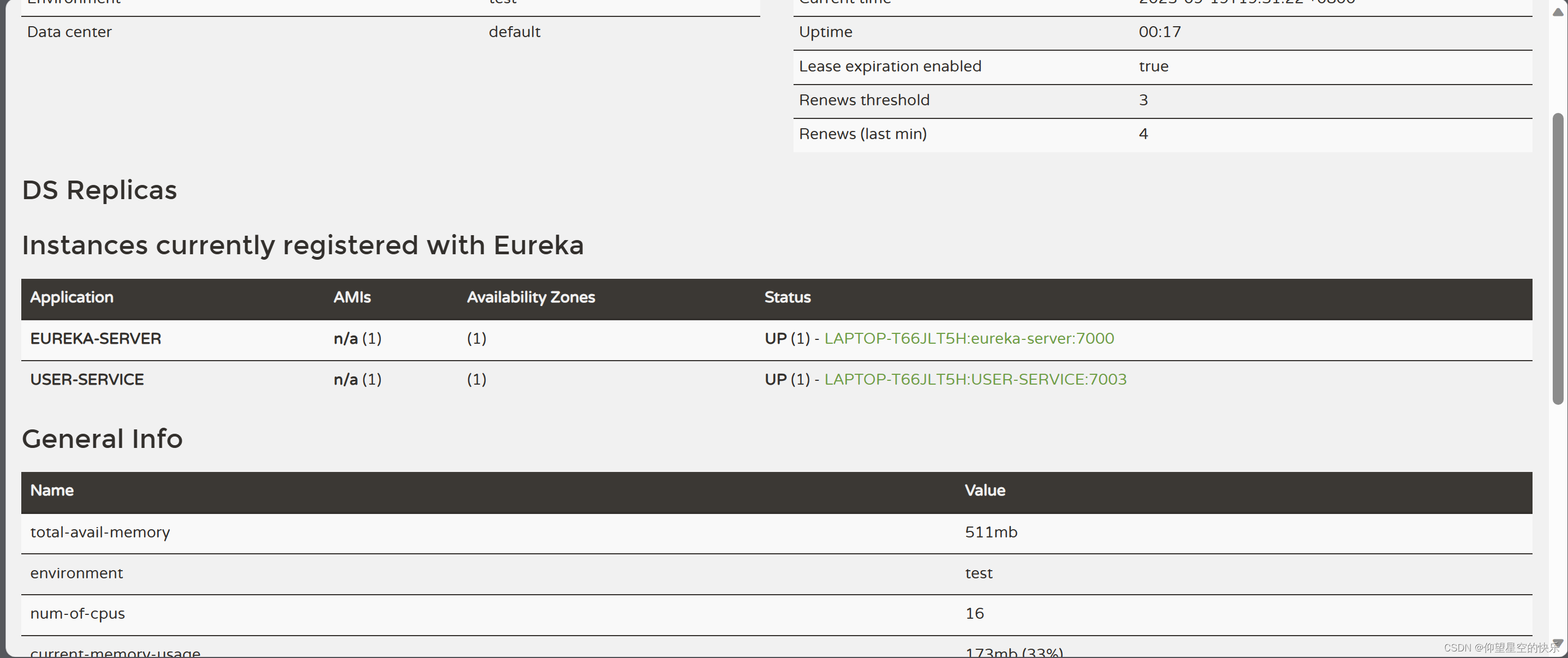
Eureka服务器注册
一。Eureka服务器注册 1.pom.xml <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://mav…...

Windows安装GPU版本的pytorch详细教程
文章目录 chatGLM2-6B安装教程正式安装 chatGLM2-6B ChatGLM2-6B版本要装pytorch2.0,而且要2.0.1 ,因此CUDA不能用12.0 ,也不能用10.0,只能用11.x 版本。 安装教程 pip install直接下载安装 官网: https://pytorch.…...

理解Kruskal算法的前提----深入理解并查集【超简单~】
并查集的实现思路 并查集主要分为两个部分:第一部分就是需要找到点对应的祖宗节点,第二部分,是要将属于同一个集合节点的祖宗节点进行统一,也就是结合操作。 Find函数实现 // parent数组用来存储下标值所对应的父节点值 // 比如…...
Jenkins+Gitee+Docker+Ruoyi项目前后端分离部署
前言 描述:本文主要是用来记录 如何用标题上的技术,部署到云服务器上通过ip正常访问。 一、总览 1.1、Docker做的事 拉取 mysql 镜像拉取 redis 镜像拉取 jdk 镜像拉取 nginx 镜像 解释说明:前端项目的打包文件放在 nginx容器运行。后端…...
)
笙默考试管理系统-MyExamTest----codemirror(23)
笙默考试管理系统-MyExamTest----codemirror(23) 目录 笙默考试管理系统-MyExamTest----codemirror(23) 一、 笙默考试管理系统-MyExamTest 二、 笙默考试管理系统-MyExamTest 三、 笙默考试管理系统-MyExamTest 四、 笙…...
 泛型)
重学Java (一) 泛型
1. 前言 泛型编程自从 Java 5.0 中引入后已经超过15个年头了。对于现在的 Java 码农来说熟练使用泛型编程已经是家常便饭的事情了。所以本文就在不对泛型的基础使用在做说明了。 如果你还不会使用泛型的话,可以参考下面两个链接 Java 泛型详解The Java™ Tutorial…...

Docker 部署 Redis 服务
拉取最新版本的 Redis 镜像: $ sudo docker pull redis:latest在本地预先创建好 data 目录和 conf/redis.conf 文件。 使用以下命令来运行 Redis 容器: $ sudo docker run -itd --name redis --privilegedtrue -p 6379:6379 -v /home/ubuntu/docker/redis/data:/data -v /ho…...
阿里云产品试用系列-负载均衡 SLB
阿里云负载均衡(Server Load Balancer,简称SLB)是云原生时代应用高可用的基本要素。通过将流量分发到不同的后端服务来扩展应用系统的服务吞吐能力,消除单点故障并提升应用系统的可用性。阿里云SLB包含面向4层的网络型负载均衡NLB…...

drf 对象级权限
drf 对象级权限 Django REST Framework(DRF)提供了对象级别权限(Object-level permissions)来控制特定对象的访问权限。 简单来说:通过视图类中的self.get_object(pk)得到一个obj对象(视图对象),在与requ…...
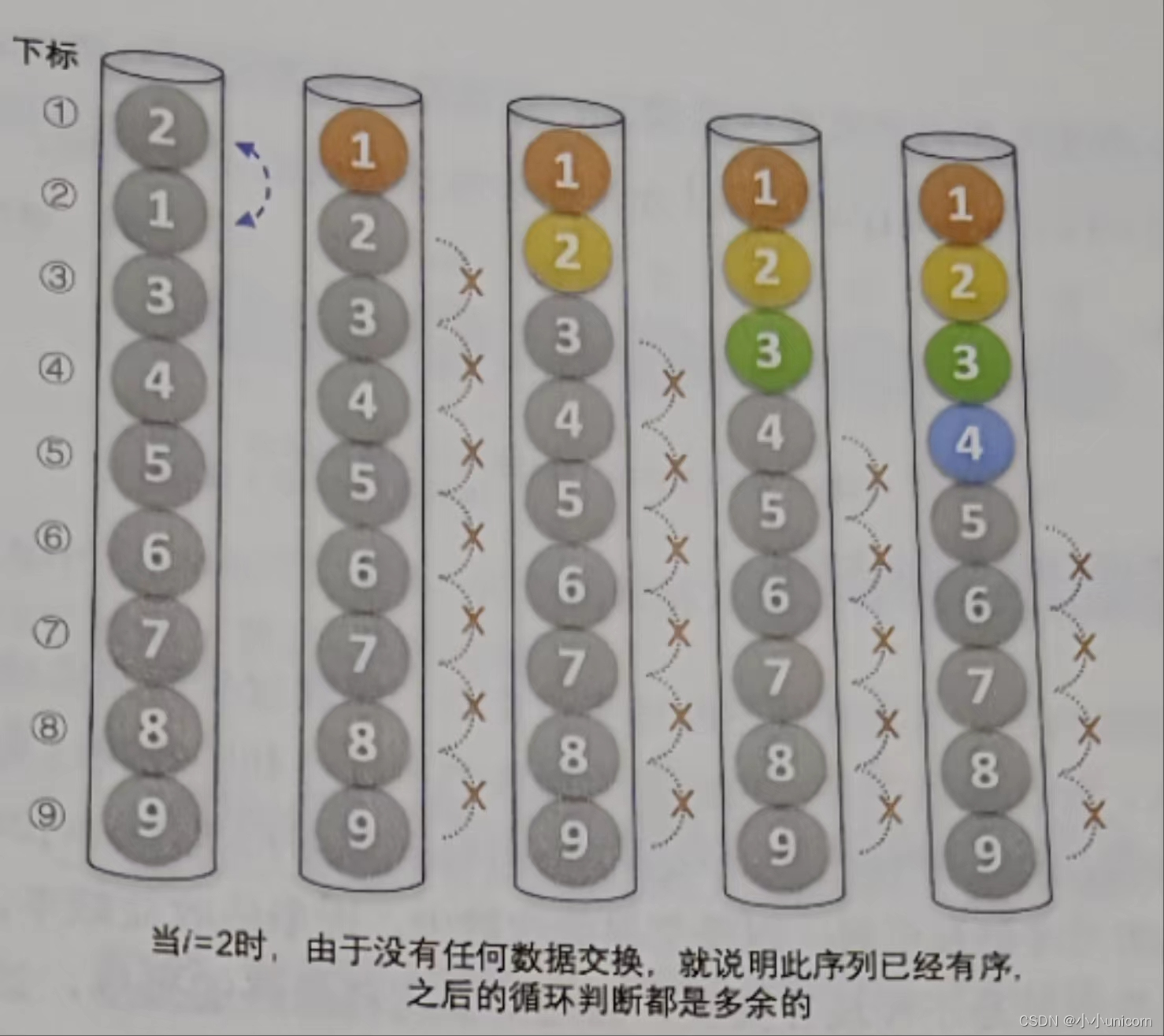
八大排序(二)--------冒泡排序
本专栏内容为:八大排序汇总 通过本专栏的深入学习,你可以了解并掌握八大排序以及相关的排序算法。 💓博主csdn个人主页:小小unicorn ⏩专栏分类:八大排序汇总 🚚代码仓库:小小unicorn的代码仓库…...
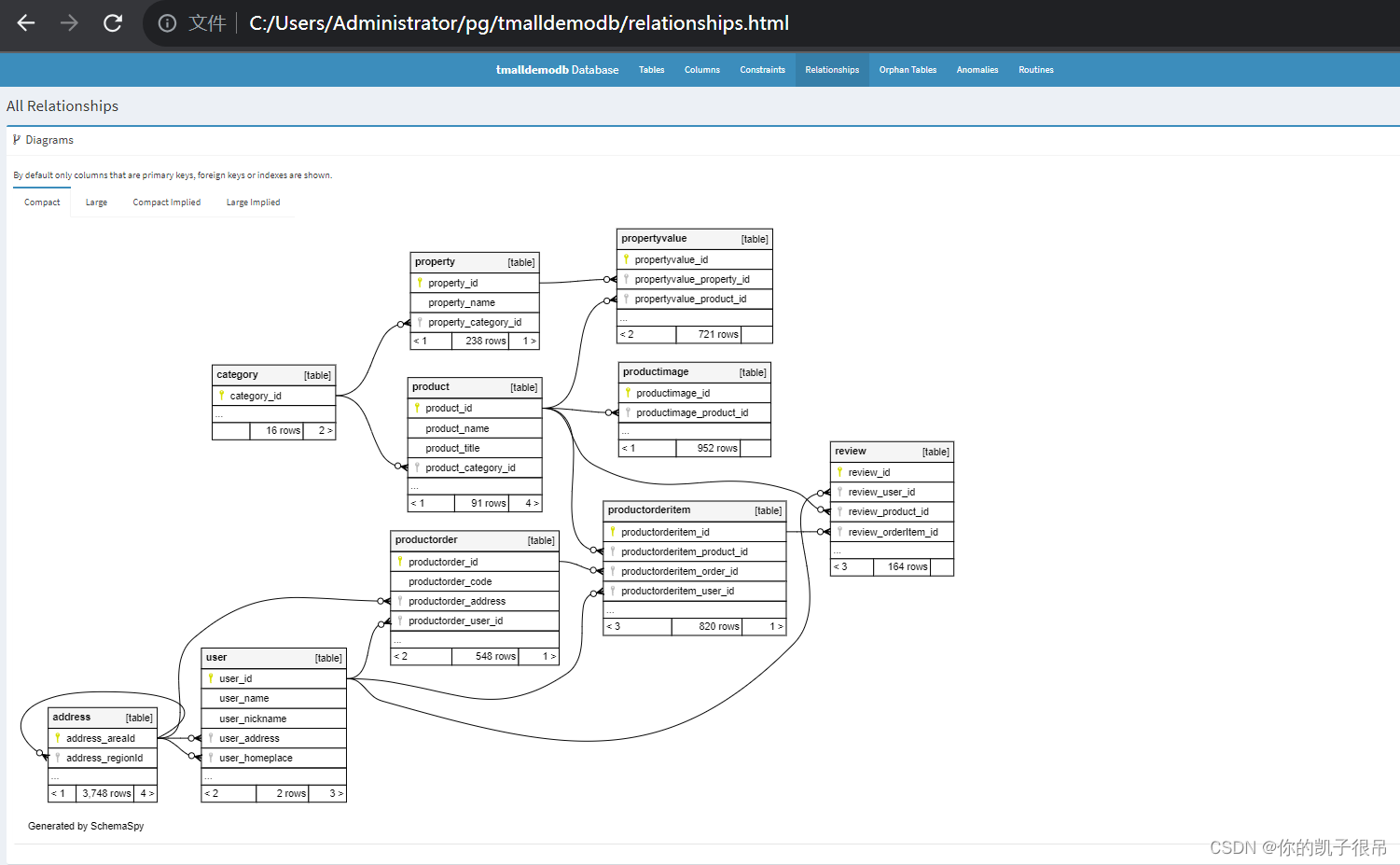
SmartSQL 一款开源的数据库文档管理工具
建议直接蓝奏云下载安装 蓝奏云下载:https://wwoc.lanzoum.com/b04dpvcxe 蓝奏云密码:123 项目介绍 SmartSQL 是一款方便、快捷的数据库文档查询、导出工具!从最初仅支持 数据库、CHM文档格式开始,通过不断地探索开发、集思广…...

代码随想录算法训练营第56天 | ● 583. 两个字符串的删除操作 ● 72. 编辑距离 ● 动态规划之编辑距离总结篇
文章目录 前言一、583. 两个字符串的删除操作二、72. 编辑距离三、动态规划之编辑距离总结篇总结 前言 一、583. 两个字符串的删除操作 两种思路:1.直接动态规划,求两个字符串需要删除的最小次数 2.采用子序列的和-最长公共子序列。思路一分析如下&#…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...
