算法通关村-----图的基本算法
图的实现方式
邻接矩阵
定义
邻接矩阵是一个二维数组,其中的元素表示图中节点之间的关系。通常,如果节点 i 与节点 j 之间有边(无向图)或者从节点 i 到节点 j 有边(有向图),则矩阵中的元素值为 1 或者表示边的权重值。如果没有边相连,则元素值为 0 或者一个特定的标记(通常表示无穷大)。
优点
适用于稠密图,即节点之间有很多边的情况,因为它不会浪费太多空间。支持常数时间内的边的查找操作。
缺点
对于稀疏图,它会浪费大量的空间,因为大部分元素都是 0。插入和删除边的操作相对较慢,需要修改矩阵的值。
邻接表
定义
邻接表是一种数据结构,用于表示图的每个节点及其相邻节点的列表。通常使用数组(或哈希表)和链表(或其他数据结构)的组合来实现。每个节点对应一个数组元素,该元素存储指向该节点相邻节点的链表或数组。
优点
适用于稀疏图,因为它不会浪费大量空间。插入和删除边的操作相对较快,因为只需要修改链表或数组。
缺点
查找两个节点之间是否存在边需要遍历相邻节点列表,时间复杂度取决于节点的度数。
图的遍历
深度优先搜索(DFS)
定义
DFS从一个起始节点开始,沿着一条边尽可能深地探索图,直到无法继续为止,然后回溯到上一个节点,继续深入其他分支。DFS通常使用递归或栈数据结构来实现。
步骤
从起始节点开始,将其标记为已访问。
对于当前节点,遍历其未被访问的邻居节点。
选择一个邻居节点,将其标记为已访问,并递归或使用栈继续探索该邻居节点。
重复步骤3,直到没有未被访问的邻居节点,然后回溯到上一个节点,继续探索其他邻居。
特点
深度优先搜索会一直沿着一条分支深入,直到到达最深处,然后返回并探索其他分支。使用递归时,可能导致堆栈溢出,因此对于大型图,可能需要使用非递归实现,使用显式的栈数据结构。
广度优先搜索(BFS)
定义
BFS从一个起始节点开始,首先访问其所有未被访问的邻居节点,然后按照距离从起始节点逐层扩展,直到遍历完整个图。BFS通常使用队列数据结构来实现。
步骤
从起始节点开始,将其标记为已访问,并将其加入队列。
从队列中取出一个节点,访问其所有未被访问的邻居节点,并将它们标记为已访问,并加入队列。
重复步骤2,直到队列为空。
特点
广度优先搜索首先访问离起始节点最近的节点,然后逐层扩展,确保了最短路径的搜索。使用队列来实现,确保了节点按照距离逐层访问。
最小生成树
概念
最小生成树(Minimum Spanning Tree,简称 MST)是在一个连通图中找到一棵包含图中所有节点的树,并且该树的所有边的权重之和最小的树。通俗地说,最小生成树是一棵树,它连接了图中的所有节点,并且总权重最小。Prim算法和Kruskal算法是两种常见的用于求解最小生成树问题的算法。
Prim算法
思想
Prim算法的关键思想是始终选择当前最小权重的边,以确保最小生成树的总权重最小。这种贪心策略保证了Prim算法的正确性。
步骤
选择一个起始节点:首先,从图中选择一个任意的起始节点作为最小生成树的根节点。
初始化:创建一个空的最小生成树,开始时只包含根节点。同时,创建一个优先队列(通常使用最小堆)来存储候选边,该队列初始化为空。
找到候选边:将起始节点的所有相邻边(连接到未包含在最小生成树中的节点的边)添加到优先队列中。
选择最小权重的边:从优先队列中选择权重最小的边(即最小的边权重),并将其添加到最小生成树中。
标记节点:将该边连接的节点标记为已访问或已包含在最小生成树中。
重复步骤3至5:不断重复步骤3和步骤4,选择并添加下一条权重最小的边,直到最小生成树包含了图中的所有节点。
结束:当最小生成树包含了所有节点时,算法终止。
特点
Prim算法的时间复杂度取决于优先队列的实现方式,通常为O(E + VlogV),其中E是边的数量,V是节点的数量。Prim算法在稠密图(边数量较多)上效果较好,因为优先队列中的边数量较多时,操作的时间复杂度较低。它适用于带权重的图,用于解决网络设计、电路设计、城市规划等问题。
Kruskal算法
思想
Kruskal算法的关键思想是始终选择权重最小的边,并确保最小生成树不形成环。这种贪心策略保证了Kruskal算法的正确性。
步骤
初始化:将图中的所有边按照权重从小到大排序,并将它们存储在一个边集合中。同时,创建一个空的最小生成树,开始时不包含任何边。
遍历边集合:按照排序后的顺序遍历边集合。
检查边的端点:对于当前遍历到的边,检查它的两个端点是否已经在最小生成树中。如果边的两个端点都不在最小生成树中,说明将这条边添加到最小生成树不会形成环,因此可以安全地将这条边加入最小生成树中。
添加边:将通过步骤3确定可以添加的边,加入到最小生成树中。
重复步骤2至4:不断重复遍历边集合并添加边,直到最小生成树包含了图中的所有节点或者边集合已经遍历完。
结束:当最小生成树包含了所有节点时,算法终止。
特点
Kruskal算法的时间复杂度主要取决于排序边的操作,通常为O(ElogE),其中E是边的数量。由于Kruskal算法不需要对节点的度数进行操作,因此在稠密图(边数量较多)上表现较好。它适用于带权重的图,用于解决网络设计、电路设计、城市规划等问题。需要注意的是,Kruskal算法不一定会生成唯一的最小生成树,但它保证了生成的最小生成树的总权重是最小的。如果存在多个最小生成树,它们的总权重将相等。
最短路径
概念
最短路径问题是图论中的一个经典问题,其目标是找到从一个指定的起始节点到另一个指定的目标节点之间的最短路径,即具有最小权重(距离、代价等)的路径。最短路径问题分为单源最短路径和所有节点对最短路径。
单源最短路径问题(Single-Source Shortest Path):在单源最短路径问题中,给定一个起始节点,要找到该节点到图中所有其他节点的最短路径。最著名的算法是Dijkstra算法。
所有节点对最短路径问题(All-Pairs Shortest Path):在所有节点对最短路径问题中,需要找到图中任意两个节点之间的最短路径。最著名的算法是Floyd算法。
Dijkstra算法
思想
Dijkstra算法的核心思想是使用贪心策略,即始终选择当前距离最短的节点进行探索,并逐步更新距离数组。由于它不处理负权重边,因此适用于带有非负权重边的图。
步骤
初始化:首先,创建一个集合(通常是一个优先队列或最小堆),用于存储尚未确定最短路径的节点。同时,初始化一个距离数组,用于记录从起始节点到每个节点的当前最短距离。将起始节点的距离设置为0,表示到达起始节点的距离为0,而其他节点的距离设置为无穷大(或一个足够大的值)表示尚未确定的距离。
选择最近的节点:从集合中选择距离起始节点最近的节点,并将其标记为当前的最短路径节点。通常,这个选择过程使用优先队列或最小堆来实现,以确保每次选择的是距离最近的节点。
更新距离:对于当前选定的最短路径节点,遍历其所有未被确定最短路径的邻居节点。计算从起始节点经过当前节点到邻居节点的距离,并将这个距离与之前记录的距离进行比较。如果新计算得到的距离更短,就更新邻居节点的距离。
重复步骤2和步骤3:不断重复选择最近的节点和更新距离的步骤,直到所有节点都被标记为确定最短路径或集合为空。
结束:当所有节点都被标记为确定最短路径时,算法终止,距离数组中存储的就是从起始节点到所有其他节点的最短路径。
特点
Dijkstra算法的时间复杂度通常为O(V^2),其中V是节点的数量。但如果使用优先队列或最小堆来实现,时间复杂度可以优化为O(E + VlogV),其中E是边的数量。因此,对于大型图来说,使用优先队列实现Dijkstra算法更有效率。算法的正确性得益于贪心策略,它保证了每一步都选择了当前最优的路径。
Floyd算法
思想
使用动态规划的方法,通过考虑所有可能的中间节点,逐步更新节点对之间的最短路径距离。这个算法可以处理带有正、负权重边的图,以及检测负权重环路。
步骤
初始化距离矩阵:创建一个距离矩阵(通常用二维数组表示),其中元素d[i][j]表示从节点i到节点j的最短距离。初始时,将矩阵中的对角线元素(i等于j的元素)设置为0,表示从节点i到节点i的距离为0。对于其他元素,如果存在直接的边连接节点i和节点j,则将d[i][j]设置为边的权重,否则将其设置为无穷大。
更新距离矩阵:对于每对节点i和j,以及中间节点k,检查是否存在一条路径从节点i到节点j,经过节点k,比当前的最短距离更短。具体步骤如下:
对于每一对节点i和j(i ≠ j),遍历所有中间节点k(1到n,其中n是节点的总数)。
计算从节点i经过节点k到节点j的距离:d[i][k] + d[k][j]。
如果上述距离小于当前的最短距离d[i][j],则更新d[i][j]为这个新的更短距离。
重复步骤2:不断重复更新距离矩阵的步骤,直到不再存在更短的路径为止。这意味着每个节点对之间的最短路径已经被找到。
结束:当算法完成后,距离矩阵d包含了所有节点对之间的最短路径距离。
特点
Floyd算法的时间复杂度为O(V^3),其中V是节点的数量。虽然它在时间复杂度上比Dijkstra算法慢,但Floyd-Warshall算法具有一个重要的优点,即可以一次性计算所有节点对之间的最短路径,因此非常适合于计算密集型问题和需要计算所有节点对的情况。
相关文章:

算法通关村-----图的基本算法
图的实现方式 邻接矩阵 定义 邻接矩阵是一个二维数组,其中的元素表示图中节点之间的关系。通常,如果节点 i 与节点 j 之间有边(无向图)或者从节点 i 到节点 j 有边(有向图),则矩阵中的元素值…...

基于随机森林+小型智能健康推荐助手(心脏病+慢性肾病健康预测+药物推荐)——机器学习算法应用(含Python工程源码)+数据集(二)
目录 前言总体设计运行环境Python环境依赖库 模块实现1. 疾病预测2. 药物推荐1)数据预处理2)模型训练及应用3)模型应用 其它相关博客工程源代码下载其它资料下载 前言 本项目基于Kaggle上公开的数据集,旨在对心脏病和慢性肾病进行…...
stm32学习-芯片系列/选型
【03】STM32HAL库开发-初识STM32 | STM概念、芯片分类、命名规则、选型 | STM32原理图设计、看数据手册、最小系统的组成 、STM32IO分配_小浪宝宝的博客-CSDN博客 STM32:ST是意法半导体,M是MCU/MPU,32是32位。 ST累计推出了:…...

LeetCode //C - 200. Number of Islands
200. Number of Islands Given an m x n 2D binary grid grid which represents a map of *‘1’*s (land) and *‘0’*s (water), return the number of islands. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically…...

使用Python构建强大的网络爬虫
介绍 网络爬虫是从网站收集数据的强大技术,而Python是这项任务中最流行的语言之一。然而,构建一个强大的网络爬虫不仅仅涉及到获取网页并解析其HTML。在本文中,我们将为您介绍创建一个网络爬虫的过程,这个爬虫不仅可以获取和保存网…...

图像处理之《基于语义对象轮廓自动生成的生成隐写术》论文精读
一、相关知识 首先我们需要了解传统隐写和生成式隐写的基本过程和区别。传统隐写需要选定一幅封面图像,然后使用某种隐写算法比如LSB、PVD、DCT等对像素进行修改将秘密嵌入到封面图像中得到含密图像,通过信道传输后再利用算法的逆过程提出秘密信息。而生…...

Java 字节流
一、输入输出流 输入输出 ------- 读写文件 输入 ------- 从文件中获取数据到自己的程序中,接收处理【读】 输出 ------- 将自己程序中处理好的数据保存到文件中【写】 流 ------- 数据移动的轨迹 二、流的分类 按照数据的移动轨迹分为:输入流 输出流…...

华硕电脑怎么录屏?分享实用录制经验!
“华硕电脑怎么录屏呀,刚买的笔记本电脑,是华硕的,自我感觉挺好用的,但是不知道怎么录屏,最近刚好要录一个教程,怎么都找不到在哪里录制,有人能教教我吗?” 随着电脑技术的不断发展…...

python学习--python的异常处理机制
try…except try:n1int(input(请输入一个整数))n2int(input(请输入另一个整数))resultn1/n2print(结果为,result) except ZeroDivisionError: print(除数不能为0)try…except…else 如果try块中没有抛出异常,则执行else块,如果try中抛出异常࿰…...
nacos+Dubbo整合快速入门
官网:Nacos Spring Boot 快速开始 下载下载链接启动:进入bin目录,startup.cmd -m standalone引入依赖 <dependency><groupId>org.apache.dubbo</groupId><artifactId>dubbo</artifactId><version>3.0.9…...
QT实现钟表
1、 头文件 #ifndef MAINWINDOW_H #define MAINWINDOW_H#include <QMainWindow> #include <QPaintEvent> //绘制事件类 #include <QDebug> //信息调试类 #include <QPainter> //画家类 #include <QTimerEve…...
准备我们心爱的IDEA写Jsp
JSP学习 一、准备我们心爱的IDEA new一个项目:New Project --> Next -->Next -->Finsh 二、配置好服务器Tomcat-9.0.30 1.> 在WEB-INF下创建一个Lib包 将jsp-api.jar复制进去,并使其生效 未生效前: 生效过程: 2.>…...
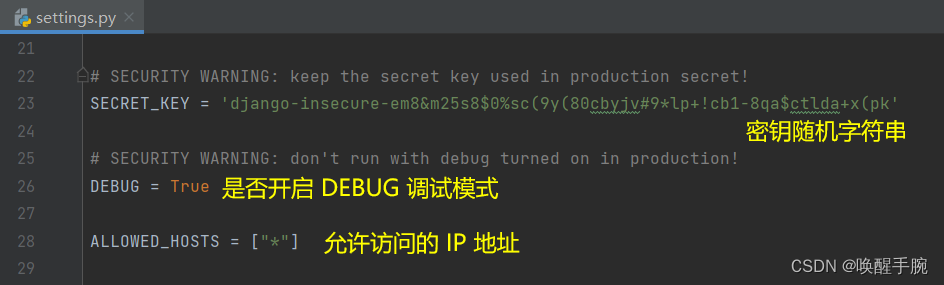
将近 5 万字讲解 Python Django 框架详细知识点(更新中)
Django 框架基本概述 Django 是一个开源的 Web 应用后端框架,由 Python 编写。它采用了 MVC 的软件设计模式,即模型(Model)、视图(View)和控制器(Controller)。在 Django 框架中&am…...
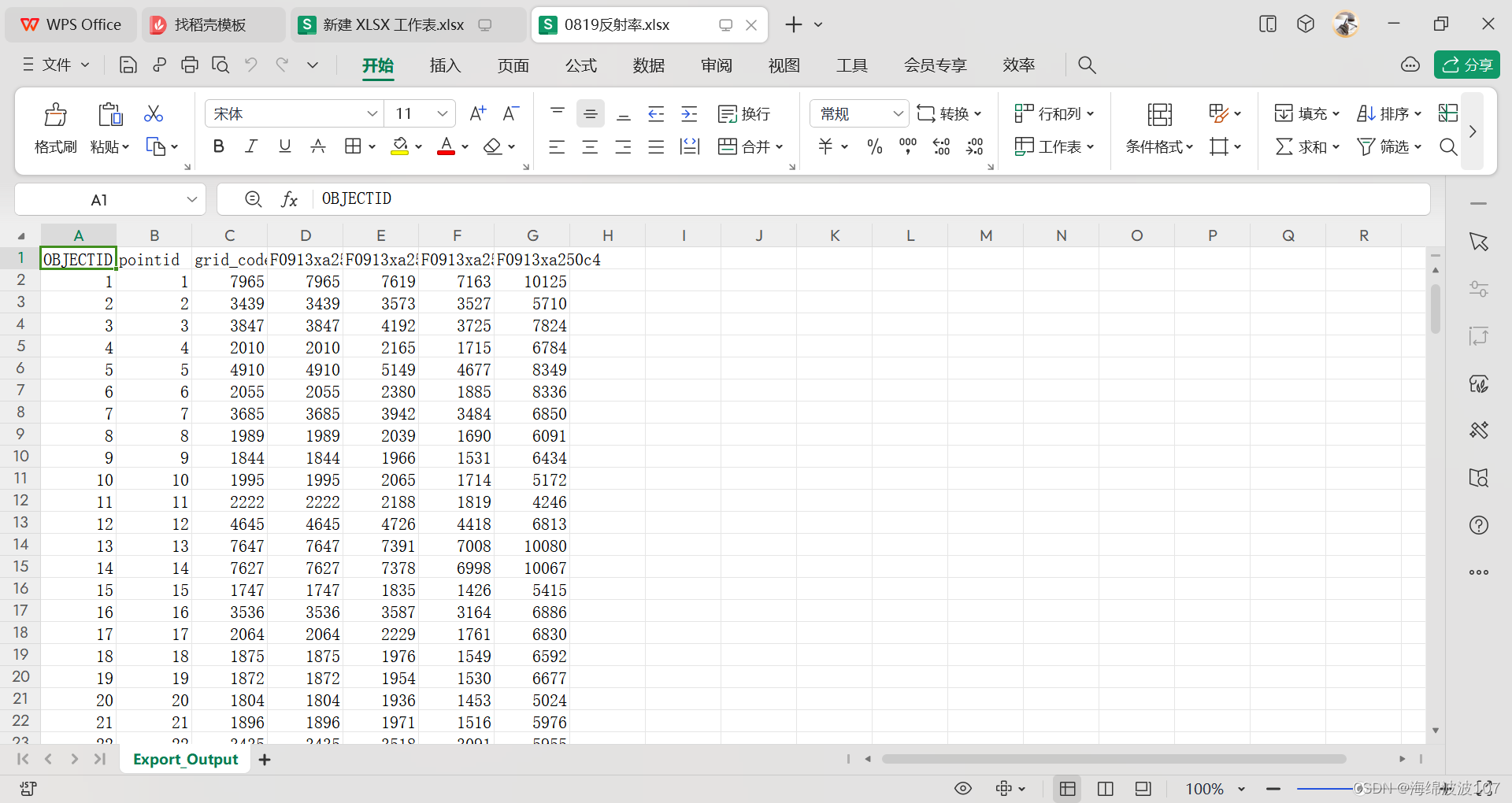
Arcgis提取每个像元的多波段反射率值
Arcgis提取每个像元的多波段反射率值 数据预处理 数据预处理阶段需要对遥感图像进行编辑传感器参数、辐射定标、大气校正、正射校正,具体流程见该文章 裁剪研究区 对于ENVI处理得到的tiff影像,虽然是经过裁剪了,但是还存在黑色的背景值&a…...
)
JavaScript面试题整理(一)
数据类型篇 1、JavaScript有哪些数据类型,它们的区别是什么? 基本数据类型:number、string、boolean、undefined、NaN、BigInt、Symbol 引入数据类型:Object NaN是JS中的特殊值,表示非数字,NaN不是数字…...

数据结构:树和二叉树之-堆排列 (万字详解)
目录 树概念及结构 1.1树的概念 1.2树的表示 编辑2.二叉树概念及结构 2.1概念 2.2数据结构中的二叉树:编辑 2.3特殊的二叉树: 编辑 2.4 二叉树的存储结构 2.4.1 顺序存储: 2.4.2 链式存储: 二叉树的实现及大小堆…...

爬虫入门基础:深入解析HTTP协议的工作过程
目录 一、HTTP协议简介 二、HTTP协议的工作过程 三、请求方法与常见用途 四、请求头与常见字段 五、状态码与常见含义 六、进阶话题和注意事项 总结 在如今这个数字化时代,互联网已经成为我们获取信息、交流和娱乐的主要渠道。而在互联网中,HTTP协…...
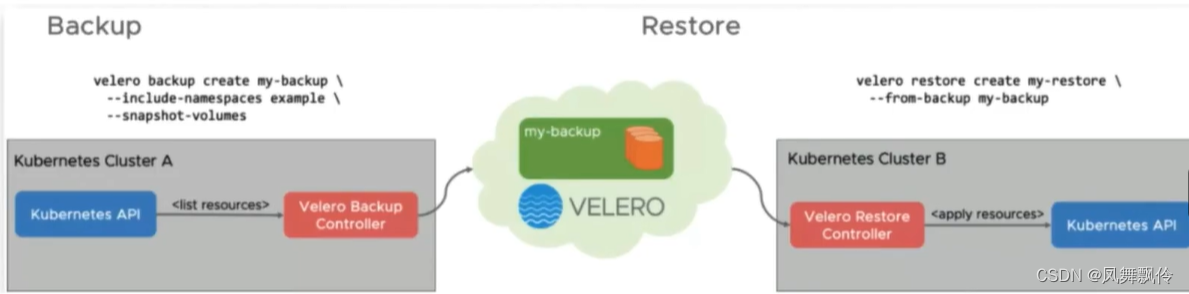
k8备份与恢复-Velero
简介 Velero 是一款可以安全的备份、恢复和迁移 Kubernetes 集群资源和持久卷等资源的备份恢复软件。 Velero 实现的 kubernetes 资源备份能力,可以轻松实现 Kubernetes 集群的数据备份和恢复、复制 kubernetes 集群资源到其他kubernetes 集群或者快速复制生产环境…...

基于Python开发的火车票分析助手(源码+可执行程序+程序配置说明书+程序使用说明书)
一、项目简介 本项目是一套基于Python开发的火车票分析助手,主要针对计算机相关专业的正在做毕设的学生与需要项目实战练习的Python学习者。 包含:项目源码、项目文档等,该项目附带全部源码可作为毕设使用。 项目都经过严格调试,…...

旺店通·企业奇门与金蝶云星空对接集成订单查询连通销售订单新增(旺店通销售-金蝶销售订单-小红书)
旺店通企业奇门与金蝶云星空对接集成订单查询连通销售订单新增(旺店通销售-金蝶销售订单-小红书) 接通系统:旺店通企业奇门 慧策最先以旺店通ERP切入商家核心管理痛点——订单管理,之后围绕电商经营管理中的核心管理诉求,先后布局流量获取、会…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
