erlang练习题(二)
题目一
替换元组或列表中指定位置的元素,新元素作为参数和列表或元组一起传入函数内
解答
replaceIdx(List, Index, Val) ->replaceIdx(List, Index, Val, 1, []).replaceIdx([], _, _, _, Acc) ->lists:reverse(Acc);%% 到达替换位置的处理replaceIdx([_ | Rest], Index, Val, Index, Acc) ->io:format("[~p]~n", [[Val | Acc]]),replaceIdx(Rest, Index, Val, Index + 1, [Val | Acc]);replaceIdx([Element | Rest], Index, Val, CurrentIndex, Acc) ->io:format("[~p]~n", [[Element | Acc]]),replaceIdx(Rest, Index, Val, CurrentIndex + 1, [Element | Acc]).
题目二
指定列表第几位之后的数据进行反转。如:指定[2,3,5,6,7,2]第3位后进行反转
解答
%% 和并两个列表
merge_list(List1, List2) ->merge_list(List1, List2, []).merge_list([], [], Acc) -> lists:reverse(Acc);
merge_list([H | T], List2, Acc) ->merge_list(T, List2, [H | Acc]);
merge_list([], [H | T], Acc) ->merge_list([], T, [H | Acc]).%% 指定列表第几位之后的数据进行反转。如:指定[2,3,5,6,7,2]第3位后进行反转为 [2,3,5,2,7,6]
reverse_n(List, N) ->Sublist = lists:sublist(List, N + 1, length(List) - N),NewSublist = lists:reverse(Sublist),merge_list(lists:sublist(List, 3), NewSublist).
题目三
对列表进行过滤,输出列表所有的奇数和偶数
解答
filteroe(List) ->Odds = [X || X<-List, X rem 2 /= 0],Evens = [X || X<-List, X rem 2 == 0],io:format("Odds = ~p ~nEvens = ~p ~n", [Odds, Evens]).
题目四
使用匿名函数对列表进行过滤,输出列表所有的奇数和偶数(可以使用API)
解答
filter_odd_even(List) ->Odds = lists:filter(fun(X) -> X rem 2 /= 0 end, List),Evens = lists:filter(fun(X) -> X rem 2 =:= 0 end, List),{Odds, Evens}.
题目五
对数字列表或者元组中所有的奇数进行求和
解答
sum_odd(List) ->lists:sum([X || X<- List, X rem 2 /= 0]).
题目六
对数字列表或元组,输出所有偶数乘以它在此列表或元组中的偶数位数
比如在列表[3,4,8,9,7,2,5]中8所在此列表中的偶数位数为2,2所在此元组中的偶数位数为3
解答
get_evens_mul_Idx(List) ->get_evens_mul_Idx(List, 1, []).%% 递归终止get_evens_mul_Idx([], _, Acc) -> lists:reverse(Acc);%% 处理遇到偶数的情况get_evens_mul_Idx([Value | Rest], Index, Acc) when Value rem 2 == 0 ->get_evens_mul_Idx(Rest, Index + 1, [Value * Index | Acc]);%% 非偶数的情况,下标增加,其他不变get_evens_mul_Idx([_ | Rest], Index, Acc) ->get_evens_mul_Idx(Rest, Index + 1, Acc).
题目七
将指定的元素插入到列表或元组中指定的位置,列表或元组中后面的元素依次向后挪动
解答
insert_at(List, Index, Val) ->insert(List, Index, Val, 1, []).insert([], _, _, _, Acc) -> lists:reverse(Acc);%% 处理Index之前的元素,原样插入insert([Value | Rest], Index, Val, CurIdx, Acc) when CurIdx /= Index ->insert(Rest, Index, Val, CurIdx + 1, [Value | Acc]);%% 到达插入位置的处理insert(List, Index, Val, Index, Acc) ->insert(List, Index, Val, Index + 1, [Val | Acc]).
题目八
用列表输出在列表或元组中查找到的的所有重复元素
解答
find_dup(Items) ->find_dup(Items, []).find_dup([], Duplicates) ->Duplicates;%% Acc 是用来存储重复值只存一次find_dup([Item | Rest], Acc) ->case lists:member(Item, Rest) and not lists:member(Item, Acc) of % 如果答案集合已经存在了重复元素,就不要加入true -> find_dup(Rest, [Item | Acc]);false -> find_dup(Rest, Acc)end.
题目九
删出列表或元组中的所有重复元素
解答
%% 思路:就是把元素加入到新的列表中,重复的不加入 0delete_dup(Items) ->delete_dup(Items, []).delete_dup([], Acc) -> Acc;delete_dup([Item | Rest], Acc) ->case lists:member(Item, Acc) of % 元素没有出现在结果集中就加入false -> delete_dup(Rest, [Item | Acc]);true -> delete_dup(Rest, Acc)end.
题目十
使用冒泡排序对列表进行排序(升序)
解答
%% 取列表头作为最大值和bubble_sort(List) ->bubble_sort(List, length(List)).bubble_sort(List, 0) -> List; % 当迭代次数为 0 时,排序完成bubble_sort(List, N) ->SortedList = bubble_pass(List, N), % 对列表进行下一趟冒泡,一个元素到达最终位置bubble_sort(SortedList, N - 1). % 递归的进行下一趟冒泡bubble_pass([X, Y | Rest], N) when X > Y ->[Y | bubble_pass([X | Rest], N - 1)]; % 如果 X > Y 就交换他们bubble_pass([X | Rest], N) ->[X | bubble_pass(Rest, N - 1)]; % 否则位置保持不变bubble_pass([], _) -> [].
相关文章:
)
erlang练习题(二)
题目一 替换元组或列表中指定位置的元素,新元素作为参数和列表或元组一起传入函数内 解答 replaceIdx(List, Index, Val) ->replaceIdx(List, Index, Val, 1, []).replaceIdx([], _, _, _, Acc) ->lists:reverse(Acc);%% 到达替换位置的处理replaceIdx([_ …...
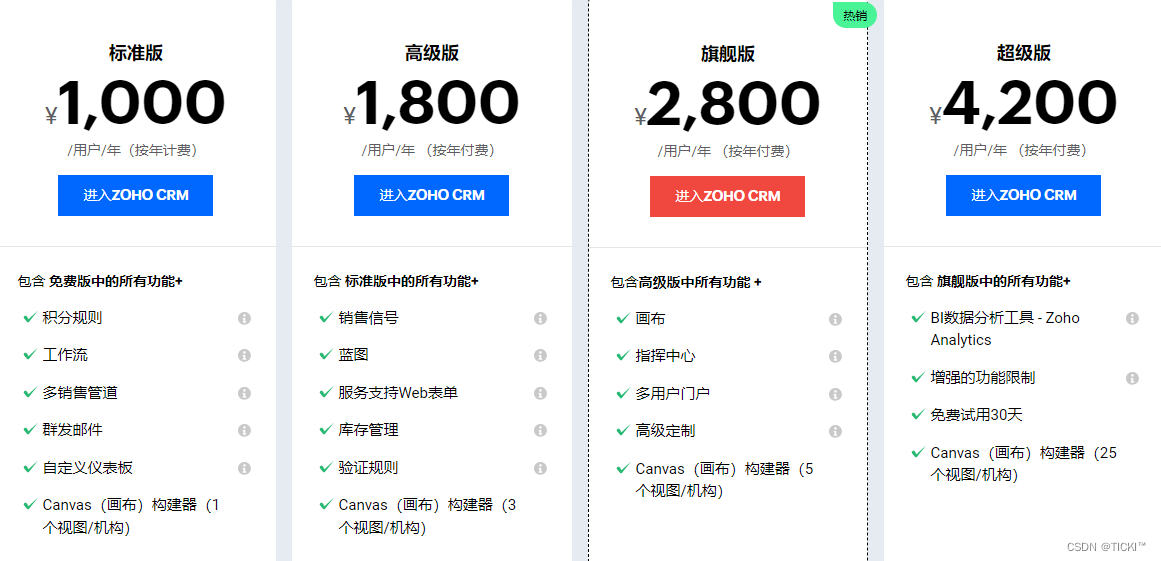
CRM软件系统价格不同的原因
很多人在了解CRM系统时,发现不同品牌的CRM价格有着很大的区别。一些CRM系统只需要几千块钱,一些CRM系统的报价却要上万,甚至十几万。为什么CRM系统价格不同?下面我们就来说说。 1、功能不同 从功能方面来说,一些CRM系…...

json数据解析
目录 一、读数据 1、简单对象读取 2、数组读取 3、对象读取 二、写数据 1、简单生成JSON 2、对象数组JSON 3、嵌套对象 三、一个综合例子 1、读JSON 2、写JSON 一、读数据 1、简单对象读取 {"app": "xnwVideo","src": "C:\\buil…...

Verilog零基础入门(边看边练与测试仿真)-状态机-笔记(7-10讲)
文章目录 第七讲第八讲第九讲第十讲 第七讲 1、最简单的状态机-三角波发生器 1、两种状态的代码: //最简单的状态机,三角波发生器; timescale 1ns/10ps module tri_gen(clk,res,d_out); input clk; input res; o…...

【Hadoop】HDFS API 操作大全
🍁 博主 "开着拖拉机回家"带您 Go to New World.✨🍁 🦄 个人主页——🎐开着拖拉机回家_Linux,大数据运维-CSDN博客 🎐✨🍁 🪁🍁 希望本文能够给您带来一定的帮助…...
Webpack打包图片
一、在js文件中引入图片 二、在package.config.js中配置加载器 module.exports {mode: "production", // 设置打包的模式:production生产模式 development开发模式module: {rules: [// 配置img加载器{test: /\.(jpg|png|gif)$/i,type:"asset/resou…...

DipC 构建基因组 3D 结构(学习笔记)
背景 本文主要记录了 DipC 数据的复现过程、学习笔记及注意事项。 目录 下载 SRA 数据使用 SRA Toolkit 转换 SRA 数据为 Fastq 格式使用 bwa 比对测序数据使用 Hickit 计算样本的基因组 3D 结构使用散点图展示 3D 结构计算 3D 结构重复模拟的稳定性其他 步骤 1. 下载 SRA…...

Qt中音频的使用
对于音频我们在使用的过程中一般是录制音频、播放音频。针对这两个需求介绍Qt中音频的使用。 Qt中音频的录制 步骤: 1、获取系统中的音频设备。 2、创建QAudioRecorder对象,指定使用的音频设备,通过QAudioRecorder的setAudioInput函数设置…...

[centos]centos7源码编译cmake报错Could NOT find OpenSSL
测试环境: centos7.9 cmake3.25.0 ./bootstrap以后报错如下: Could NOT find OpenSSL, try to set the path to OpenSSL root folder in the system variable OPENSSL_ROOT_DIR (missing: OPENSSL_CRYPTO_LIBRARY OPENSSL_INCLUDE_DIR) CMake Error …...
vue若依前端项目搭建
1.项目搭建 首先进入到你需要创建的项目目录下面,然后输入命令vue create .创建项目 接下来选择手动搭建,然后把下面图片中的内容选上 再然后继续配置一些参数信息 接下来运行npm run serve项目就启动起来了 2.配置登录界面文件 首先修改src/router…...
基于win32实现TB登陆滑动验证
这里写目录标题 滑动验证触发条件:失败条件:解决方法:清除cooKie 滑动验证方式一:win32 api获取窗口句柄,选择固定位置 成功率高方式二: 原自动化滑动,成功率中 案例 先谈理论,淘宝 taobao.com …...

vue学习-07todoList案例与浏览器本地存储
TodoList Todo List(任务列表)是一个简单的Web应用程序示例,用于管理任务、代办事项或清单。Vue.js 是一个非常适合构建这种类型应用程序的框架,因为它提供了数据绑定、组件化、响应式和轻松管理用户界面的能力。 以下是一个基本…...

探索智能应用的基石:多模态大模型赋能文档图像处理
目录 0 写在前面1 文档图像分析新重点2 token荒:电子文档助力大模型3 大模型赋能智能文档分析4 文档图像大模型应用可能性4.1 专有大模型4.2 多模态模型4.3 设计思路 总结 0 写在前面 中国智能产业高峰论坛(CIIS2023)旨在为政企研学各界学者专家提供同台交流的机会…...

自动化发布npm包小记
1.注册npm账号 打开npm官网,并注册自己的npm账号 2.申请AccessToken 1.登录npm官网,登录成功后,点开右上角头像,并点击Access Tokens选项 2.点开Generate New Token下拉框,点击Classic Token(和Granular Access To…...
详解机器视觉性能指标相关概念——混淆矩阵、IoU、ROC曲线、mAP等
目录 0. 前言 1. 图像分类性能指标 1.1 混淆矩阵(Confusion Matrix) 1.2 准确率(Precision) 1.3 召回率(Recall) 1.4 F1值(F1 score) 1.5 ROC曲线(接收者工作特征曲线,Receiver Operating Characteristic curve) 1.6 mAP(mean Average Precision) 2. 图像分…...
想要精通算法和SQL的成长之路 - 预测赢家
想要精通算法和SQL的成长之路 - 预测赢家 前言一. 预测赢家二. 石子游戏(预测赢家的进阶版)2.1 博弈论 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 预测赢家 原题链接 主要思路: 我们定义dp[i][j]:在区间 [i, j] 之间先…...
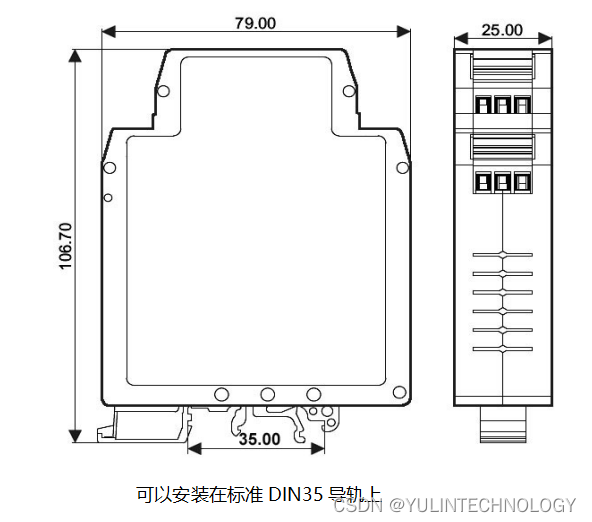
高精度PWM脉宽调制信号转模拟信号隔离变送器1Hz~10KHz转0-5V/0-10V/1-5V/0-10mA/0-20mA/4-20mA
主要特性: >>精度等级:0.1级。产品出厂前已检验校正,用户可以直接使用 >>辅助电源:8-32V 宽范围供电 >>PWM脉宽调制信号输入: 1Hz~10KHz >>输出标准信号:0-5V/0-10V/1-5V,0-10mA/0-20mA/4-20mA等&…...
Vue路由和Node.js环境搭建
文章目录 一、vue路由1.1 简介1.2 SPA1.3 实例 二、Node.js环境搭建2.1 Node.js简介2.2 npm2.3 环境搭建2.3.1 下载解压2.3.2 配置环境变量2.3.3 配置npm全局模块路径和cache默认安装位置2.3.4 修改npm镜像提高下载速度 2.4 运行项目 一、vue路由 1.1 简介 Vue 路由是 Vue.js…...

【Vue】使用vue-cli搭建SPA项目的路由,嵌套路由
一、SPA项目的构建 1、前期准备 我们的前期的准备是搭建好Node.js,测试: node -v npm -v2、利用Vue-cli来构建spa项目 2.1、什么是Vue-cli Vue CLI 是一个基于 Vue.js 的官方脚手架工具,用于自动生成vue.jswebpack的项目模板,它可以帮助开发者…...
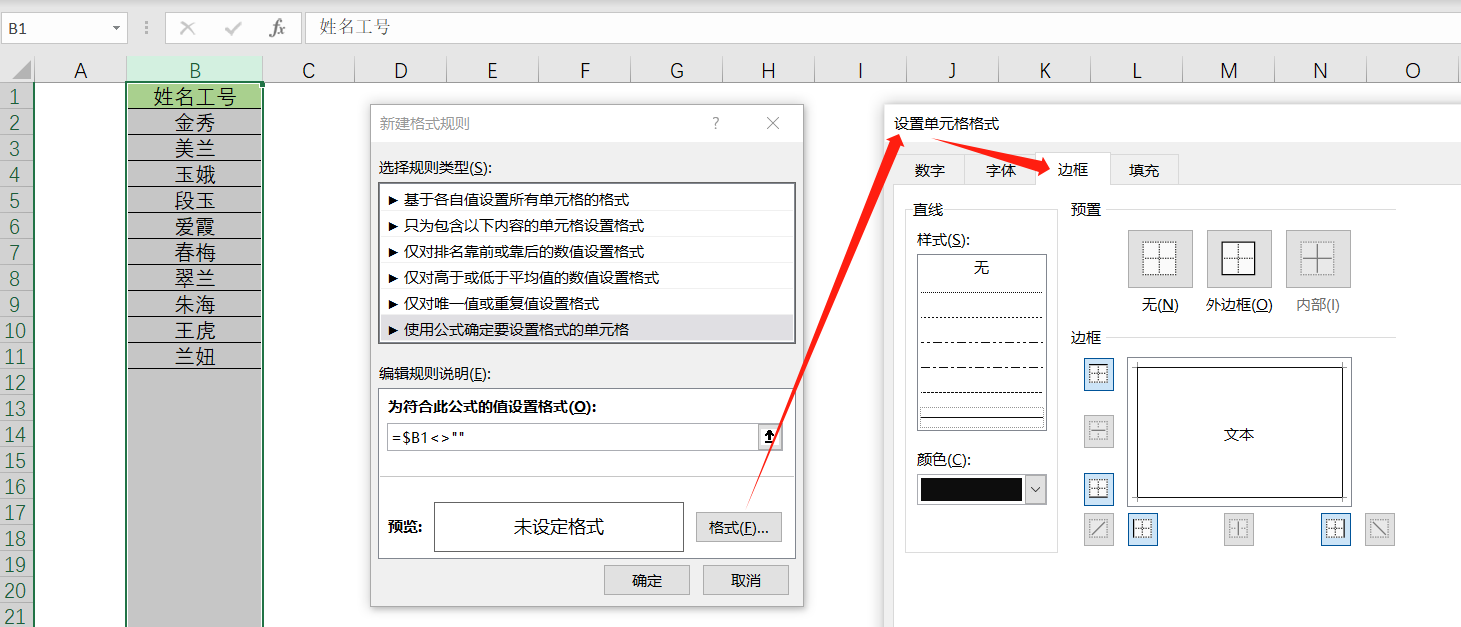
Excel 通过条件格式自动添加边框
每录入一次数据就需要手动添加一次边框,非常麻烦,这不是我们想要的。 那么有没有办法,在我们录入数据后,自动帮我们加上边框呢? 选中要自动添加边框的列,然后按箭头流程操作 ↓ ↓ ↓ ↓...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...
