算法通过村第七关-树(递归/二叉树遍历)黄金笔记|迭代遍历
文章目录
- 前言
- 1. 迭代法实现前序遍历
- 2. 迭代法实现中序遍历
- 3. 迭代法实现后序遍历
- 总结
前言
提示:在一个信息爆炸却多半无用的世界,清晰的见解就成了一种力量。 --尤瓦尔·赫拉利《今日简史》
你是不是觉得上一关特别简单,代码少,背下来就行了,但是如果你要真的理解透了,尝试一下这个一关的练习,用迭代的方式在展示一下,我们就看看非递归方式实现过程。
当然在面试的时候,如果你靠二叉树的前中后序遍历,面试官很可能不让你使用递归方式,因为太简单,可能会点名要你采用迭代的方式,所以这种方式也是必要掌握的。
理论上,递归可以解决的事情都可以通过迭代的方式解决,但是会很复杂,上面的几个递归遍历方法,背下来但是面试的时候不要求使用你就很难受的。
递归就是每次执行方法调用都会先把当前的局部变量、参数值和返回地址等压入栈中,后面再递归返回的时候,从栈顶弹出上一层的各项参数继续执行,这就是递归为什么自动返回并执行上一层方法的原因。我们这里采用迭代方法练习这三道题:
推荐题目⭐⭐⭐⭐:
144. 二叉树的前序遍历 - 力扣(LeetCode)
94. 二叉树的中序遍历 - 力扣(LeetCode)
145. 二叉树的后序遍历 - 力扣(LeetCode)
1. 迭代法实现前序遍历
前序遍历是中左右,如果还有子树就是一直向下找。完了之后再返回从最底层逐步向上向右找。不难写出代码,但是要主以空节点不如栈。
/*** 二叉树的前序遍历* @param root* @return*/public static List<Integer> preOrderTraversal(TreeNode root) {// 校验参数if (root == null){return new ArrayList<Integer>();}// 创建空间List<Integer> res = new ArrayList<Integer>();Deque<TreeNode> stack = new LinkedList<>();// 保留根节点TreeNode node = root;// 只要根节点不空或者栈不空 就循环遍历while(!stack.isEmpty() || node != null){// 中左右while(node != null){res.add(node.val);stack.push(node);node = node.left;}node = stack.pop();node = node.right;}return res;}2. 迭代法实现中序遍历
再来看看中序遍历,中序遍历时左中右,先访问的时二叉树的左子树,然后再一层一层向下访问,知道达到树的最左底部,在处理节点(也就是把节点数值放入res列表)。在使用迭代法写中序遍历,就需要借助指针的遍历帮助访问节点,栈则用来处理节点上的元素。
看下代码实现:
/*** 二叉树中序遍历* @param root* @return*/public static List<Integer> inorderTraversal (TreeNode root) {// 参数检验if (root == null){return new ArrayList<Integer>();}// 创建空间List<Integer> res = new ArrayList<Integer>();// 栈存储引用Deque<TreeNode> stack = new LinkedList<>();// 根节点不为空或者栈不为空 一直向下遍历while (root != null ||!stack.isEmpty() ) {while(root != null){stack.push(root);root = root.left;}root = stack.pop();res.add(root.val);root = root.right;}return res;}3. 迭代法实现后序遍历
后续遍历的非递归方法有三种基本实现思路
- 反转法
- 访问标记法
- Morris法
说是话这三种方法理解起来都有些难度,如果你想挑战一下你的头发,我觉得你可以试一试。
个人觉得访问标记法时最难理解的方法,Morris法时国外的大佬发明的巧思:不是用栈,而使用树中大量的空闲指针完成的,但是实现起来也是很麻烦。感兴趣的同学可以参考这篇文章看下:
【递归+迭代详解】二叉树的morris遍历、层序遍历、前序遍历、中序遍历、后序遍历_morris 递归_威斯布鲁克.猩猩的博客-CSDN博客
这里你们估计已经猜到我们要使用那种方法了:反转发。
我们看下图:
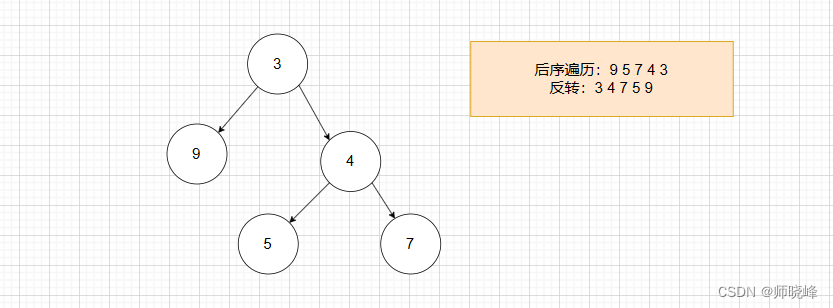
我们可以看到后序遍历的结果是seq = {9 5 7 4 3 },我们将其反转后的结果是 new_seq = {3 4 7 5 9}.
你有没有发现有什么不一样的地方,看new_seq的序列是不是和前序的思路几乎一致,只不过是左右反了,前序是先中间然后再左右,这里变成了先中间然后再右左。我们完全可以改造一下前序遍历的思路,得到序列new_seq之后,然后再将结果反转过来就是我们想要的结果了。
这真是个天才🤔:
/*** 反转法实现** @param root* @return*/public static List<Integer> postOrderTraversal(TreeNode root) {// 参数校验if (root == null) {return new ArrayList<Integer>();}// 创建空间List<Integer> res = new ArrayList<Integer>();Deque<TreeNode> stack = new LinkedList<TreeNode>();// 保留根节点信息TreeNode node = root;// 根节点不为空或者栈不为空,不断遍历下去while (!stack.isEmpty() || node != null) {while (node != null) {res.add(node.val);stack.push(node);node = node.right;}node = stack.pop();node = node.left;}// 重新反转分到结果集Collections.reverse(res);return res;}
这个方法可以巧妙的避开后序遍历的坑,感兴趣的同学可以从后续慢慢写,研究下他的妙处。
总结
提示:二叉树的迭代遍历;栈的思想;反转法
相关文章:

算法通过村第七关-树(递归/二叉树遍历)黄金笔记|迭代遍历
文章目录 前言1. 迭代法实现前序遍历2. 迭代法实现中序遍历3. 迭代法实现后序遍历总结 前言 提示:在一个信息爆炸却多半无用的世界,清晰的见解就成了一种力量。 --尤瓦尔赫拉利《今日简史》 你是不是觉得上一关特别简单,代码少,背…...
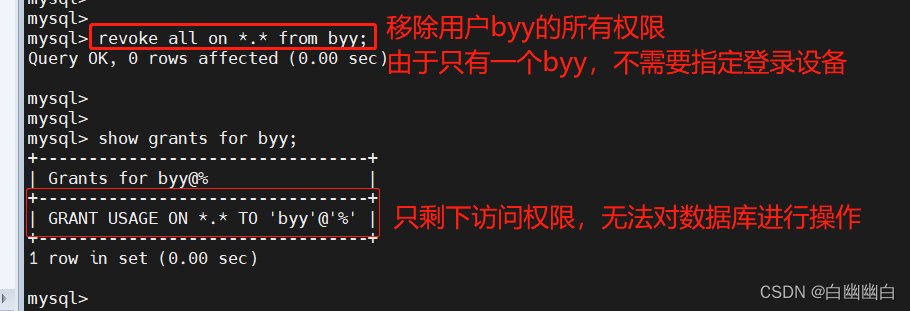
MySQL数据库简介+库表管理操作+数据库用户管理
Mysql Part 1 一、数据库的基本概念1.1 使用数据库的必要性1.2 数据库基本概念1.2.1 数据(Data)1.2.2 表1.2.3 数据库1.2.4 数据库管理系统(DBMS)1.2.5 数据库系统 1.3 数据库的分类1.3.1 关系数据库 SQL1.3.2 非关系数据库 NoSQL…...
PyTorch实战:卷积神经网络详解+Python实现卷积神经网络Cifar10彩色图片分类
目录 前言 一、卷积神经网络概述 二、卷积神经网络特点 卷积运算 单通道,二维卷积运算示例 单通道,二维,带偏置的卷积示例 带填充的单通道,二维卷积运算示例 Valid卷积 Same卷积 多通道卷积计算 1.局部感知域 2.参数共…...
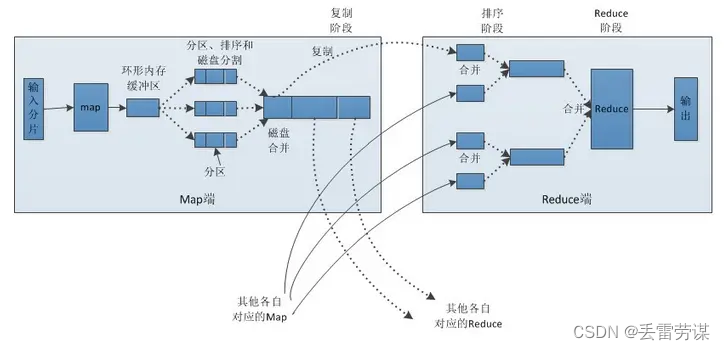
MapRdeuce工作原理
hadoop - (三)通俗易懂地理解MapReduce的工作原理 - 个人文章 - SegmentFault 思否 MapReduce架构 MapReduce执行过程 Map和Reduce工作流程 (input) ->map-> ->combine-> ->reduce-> (output) Map: Reduce...

完整指南:使用JavaScript从零开始构建中国象棋游戏
引言 中国象棋,又被称为国际象棋,是一款起源于中国的古老棋类游戏。本文旨在为大家提供一个简单明了的步骤,教你如何使用JavaScript从零开始构建这款经典的棋类游戏。 1. 游戏简介 在中国象棋中,两方各有一军队,包括…...

PG-DBA培训19:PostgreSQL高可用集群项目实战之Patroni
一、风哥PG-DBA培训19:PostgreSQL高可用集群项目实战之Patroni 课程目标: 本课程由风哥发布的基于PostgreSQL数据库的系列课程,本课程属于PostgreSQL主从复制与高可用集群阶段之PostgreSQL高可用集群项目实战之Patroni,学完本课…...
数据库管理-第105期 安装Database Valut组件(20230919)
数据库管理-第105期 安装Database Valut组件(20230919) 之前无论是是EXPDP还是PDB中遇到的一些问题,其实都跟数据库的DV(Database Valut)组件有关,因为目标库没有安装DV导致启动时会出现问题。 1 DV/OLS …...
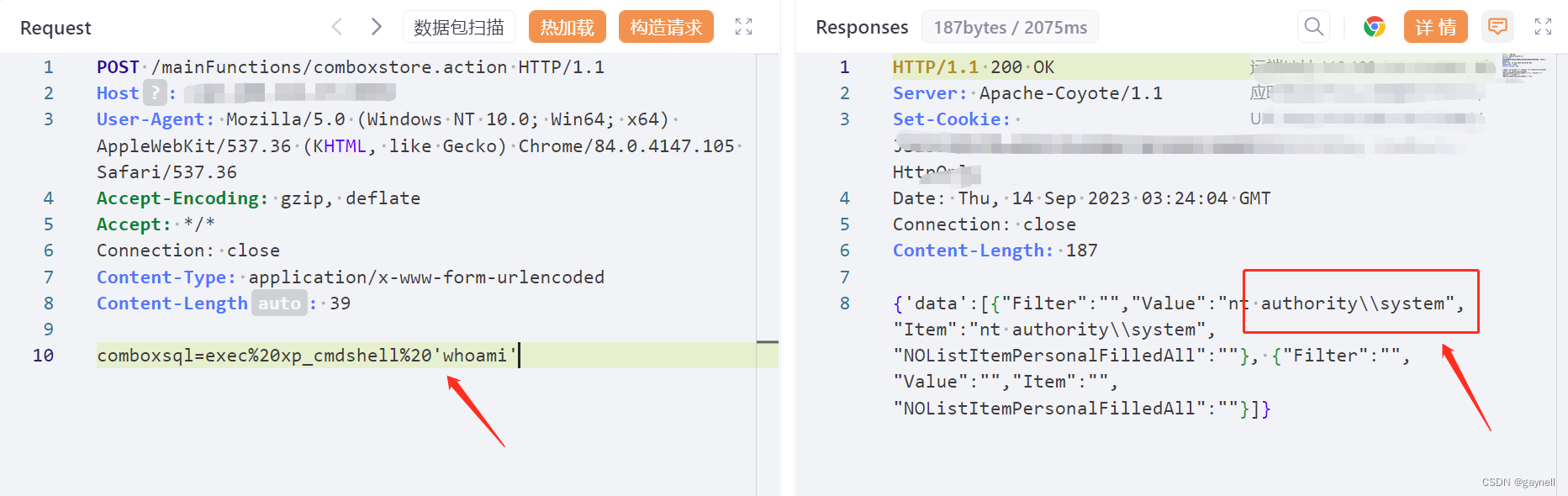
企望制造ERP系统RCE漏洞 复现
文章目录 企望制造ERP系统RCE漏洞 复现0x01 前言0x02 漏洞描述0x03 影响平台0x04 漏洞环境0x05 漏洞复现1.访问漏洞环境2.构造POC3.复现 0x06 修复建议 企望制造ERP系统RCE漏洞 复现 0x01 前言 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播…...

【unity小技巧】Unity 存储存档保存——PlayerPrefs、JsonUtility和MySQL数据库的使用
文章目录 前言PlayerPrefs一、基本介绍二、Demo三、优缺点 JsonUtility一、基本使用二、Demo三、优缺点 Mysql(扩展)完结 前言 游戏存档不言而喻,是游戏设计中的重要元素,可以提高游戏的可玩性,为玩家提供更多的自由和…...

2023-9-22 滑雪
题目链接:滑雪 #include <cstring> #include <algorithm> #include <iostream>using namespace std;const int N 310;int n, m; int h[N][N]; int f[N][N];int dx[4] {-1, 0, 1, 0}, dy[4] {0, 1, 0, -1};int dp(int x, int y) {int &v f…...

基于Yolov8的工业小目标缺陷检测(6):多检测头结合小缺陷到大缺陷一网打尽的轻量级目标检测器GiraffeDet,暴力提升工业小目标缺陷检测能力
💡💡💡本文改进:多头检测器结合大小缺陷一网打尽的GiraffeDet,进一步提升处理低分辨率图像和小物体等更困难的检测能力。 多头检测器+ GiraffeDet | 亲测在工业小目标缺陷涨点明显,原始mAP@0.5 0.679提升至0.734 收录专栏: 💡💡💡深度学习工业缺陷检测 :h…...
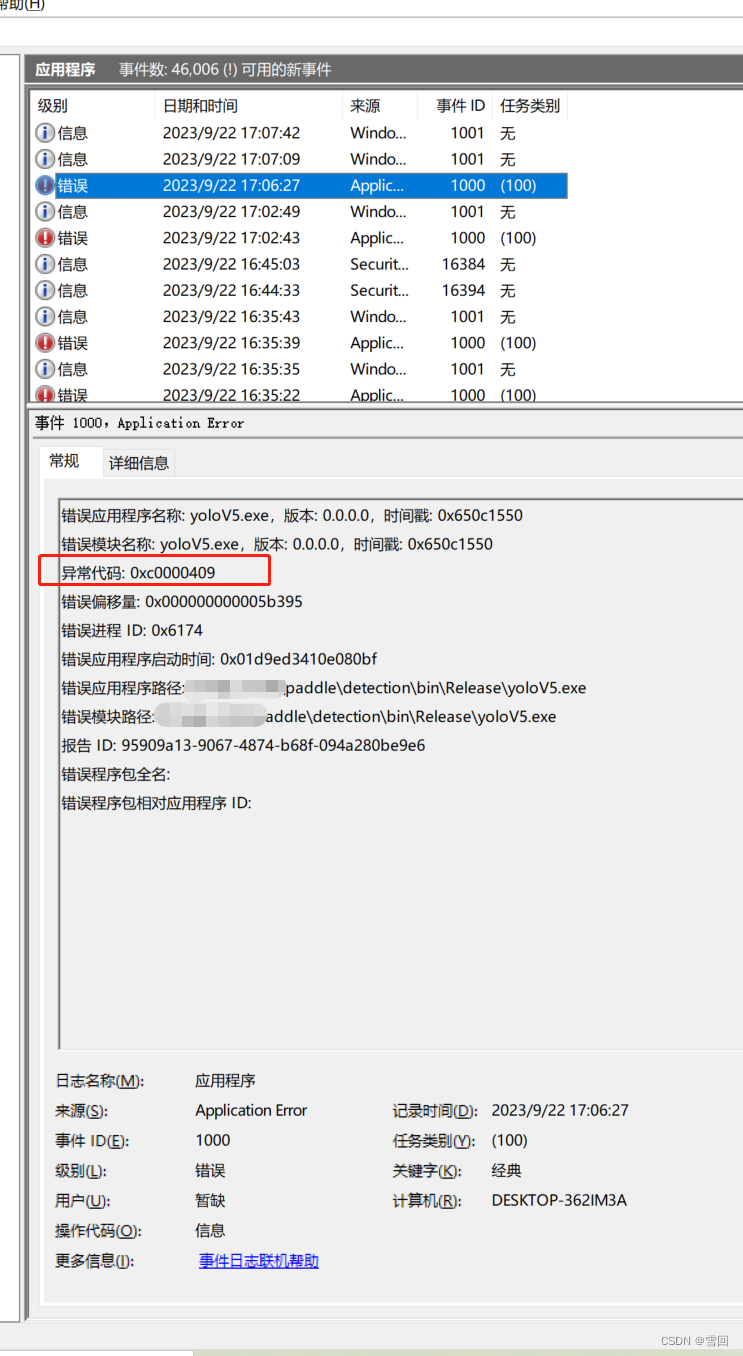
exe文件运行后无输出直接闪退如何找解决办法
一.搜索栏搜事件查看器 二.点开windows日志下的应用程序 三.找到错误处 四.搜索异常代码 点开有错误的详细信息,直接用搜索引擎搜索这个异常代码能大致判断是什么问题,给了一个解决思路,不至于不知道到底哪里出了问题...

OpenHarmony应用开发—ArkUI组件集合
介绍 本示例为ArkUI中组件、通用、动画、全局方法的集合。 效果预览 使用说明: 1.点击组件、通用、动画、全局方法四个按钮或左右滑动切换不同视图。 2.点击二级导航(如通用属性、通用事件等),若存在三级导航则展开三级导航&#…...
Linux(CentOS)安装msf
目录 一、安装MSF 1.1 在线安装 1.2 离线安装 二、安装Postgresql数据库 一、安装MSF 1.1 在线安装 需要挂梯子!挂完梯子需要reboot重启,多试几次就可以,国内网络我试了很久都不行。没条件没梯子的看1.2离线安装 cd /opt curl https://ra…...

工作几年还是悟不懂自动化测试的意义
【软件测试面试突击班】如何逼自己一周刷完软件测试八股文教程,刷完面试就稳了,你也可以当高薪软件测试工程师(自动化测试) 有人问:自动化测试的成本高效果差,那么自动化测试的意义在哪呢? 我…...

Redis面试问题三什么是缓存雪崩怎么解决
定义 缓存雪崩是因为大量的key设置了同一过期时间的导致在同一时间类缓存同时过期,而这时因为请求过来已经没有缓存了,DB压力大数据库崩溃了。 解决方法 我可以在设置过期时间的时候加一个随机时间,在1-5分钟那样可以分散过期时间…...

【Unittest】自动化测试框架核心要素
【软件测试面试突击班】如何逼自己一周刷完软件测试八股文教程,刷完面试就稳了,你也可以当高薪软件测试工程师(自动化测试) 1、什么是Unittest框架? python自带一种单元测试框架 2、为什么使用UnitTest框架࿱…...
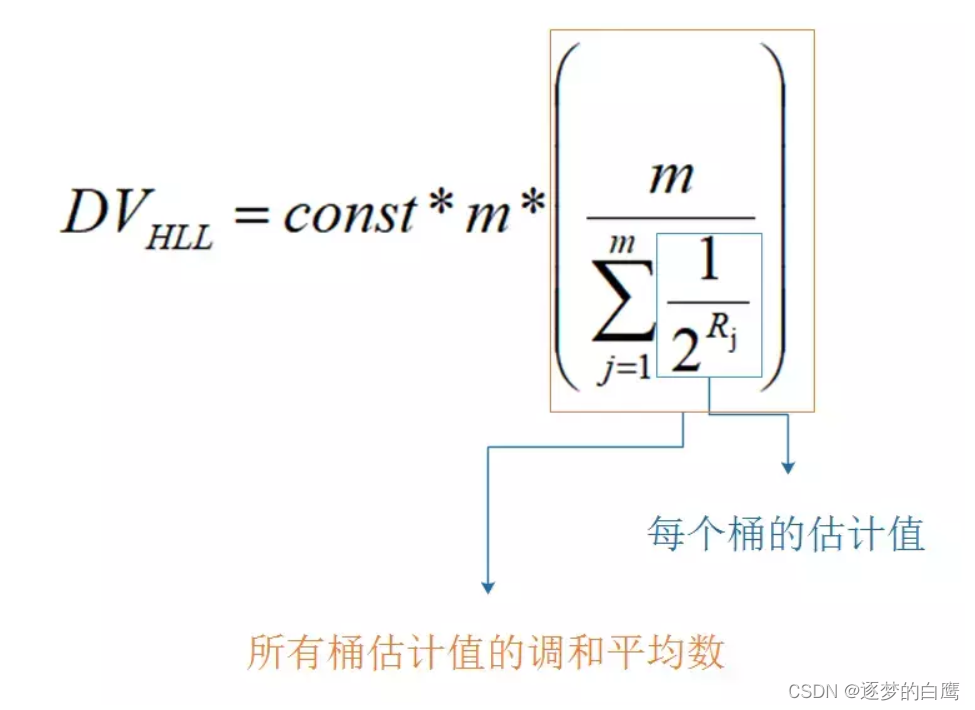
Hyperloglog
一,前言 在互联网行业中存在两个比较重要的指标:PV(页面访问量)和 UV(用户访问量) 如果有这样的一个业务: 统计PV,那么你会怎么做? 我们可以使用Redis的incr、incrby指…...

如何自动获取短信验证码?
点击下方关注我,然后右上角点击...“设为星标”,就能第一时间收到更新推送啦~~~ 这篇文章通过解决实际项目开发中遇到的如何自动获取短信验证码的问题,进一步讲述在Java中如何使用正则。 Java中如何使用正则 Java中正则相关类位于java.util.r…...
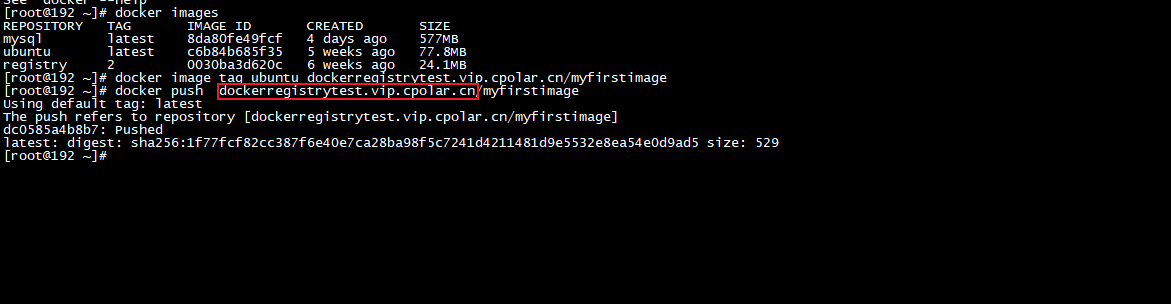
Linux 本地 Docker Registry本地镜像仓库远程连接【内网穿透】
Linux 本地 Docker Registry本地镜像仓库远程连接 文章目录 Linux 本地 Docker Registry本地镜像仓库远程连接1. 部署Docker Registry2. 本地测试推送镜像3. Linux 安装cpolar4. 配置Docker Registry公网访问地址5. 公网远程推送Docker Registry6. 固定Docker Registry公网地址…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...
