Julia 数据类型
在编程语言中,都有基本的数学运算和科学计算,它们常用的数据类型为整数和浮点数。
另外还有一个"字面量"的术语,字面量(literal)用于表达源代码中一个固定值的表示法(notation),整数、浮点数以及字符串等等都是字面量。
例如:
a=1 // a 是变量,1 是整型字面量 b=1.0 // b 是变量,1.0 是浮点型字面量
Julia 提供了很丰富的原始数值类型,并基于它们定义了一整套算术运算操作,另外还提供按位运算符以及一些标准数学函数。
整数类型
下表列出来 Julia 支持的整数类型:
| 类型 | 带符号? | 比特数 | 最小值 | 最大值 |
|---|---|---|---|---|
| Int8 | ✓ | 8 | -2^7 | 2^7 – 1 |
| UInt8 | 8 | 0 | 2^8 – 1 | |
| Int16 | ✓ | 16 | -2^15 | 2^15 – 1 |
| UInt16 | 16 | 0 | 2^16 – 1 | |
| Int32 | ✓ | 32 | -2^31 | 2^31 – 1 |
| UInt32 | 32 | 0 | 2^32 – 1 | |
| Int64 | ✓ | 64 | -2^63 | 2^63 – 1 |
| UInt64 | 64 | 0 | 2^64 – 1 | |
| Int128 | ✓ | 128 | -2^127 | 2^127 – 1 |
| UInt128 | 128 | 0 | 2^128 – 1 | |
| Bool | N/A | 8 | false (0) | true (1) |
整数字面量形式:
实例
julia> 1
1
julia> 1234
1234
整型字面量的默认类型取决于目标系统是 32 位还是 64 位架构(目前大部分系统都是 64 位):
实例
# 32 位系统:
julia> typeof(1)
Int32
# 64 位系统:
julia> typeof(1)
Int64
Julia 的内置变量 Sys.WORD_SIZE 表明了目标系统是 32 位还是 64 位架构:
实例
# 32 位系统:
julia> Sys.WORD_SIZE
32
# 64 位系统:
julia> Sys.WORD_SIZE
64
Julia 也定义了 Int 与 UInt 类型,它们分别是系统有符号和无符号的原生整数类型的别名。
实例
# 32 位系统:
julia> Int
Int32
julia> UInt
UInt32
# 64 位系统:
julia> Int
Int64
julia> UInt
UInt64
溢出行为
在 Julia 里,超出一个类型可表示的最大值会导致环绕 (wraparound) 行为:
实例
julia> x = typemax(Int64)
9223372036854775807
julia> x + 1
-9223372036854775808
julia> x + 1 == typemin(Int64)
true
因此,Julia 的整数算术实际上是模算数的一种形式,它反映了现代计算机实现底层算术的特点。在可能有溢出产生的程序中,对最值边界出现循环进行显式检查是必要的。否则,推荐使用任意精度算术中的 BigInt 类型作为替代。
下面是溢出行为的一个例子以及如何解决溢出:
实例
julia> 10^19
-8446744073709551616
julia> big(10)^19
10000000000000000000
除法错误
在以下两种例外情况下,整数除法会触发 DivideError 错误:
- 除以零
- 除以最小的负数
rem 取余函数和 mod 取模函数在除零时抛出 DivideError 错误,实例如下:
实例
julia> mod(1, 0)
ERROR: DivideError: integer division error
Stacktrace:
[1] div at .\int.jl:260 [inlined]
[2] div at .\div.jl:217 [inlined]
[3] div at .\div.jl:262 [inlined]
[4] fld at .\div.jl:228 [inlined]
[5] mod(::Int64, ::Int64) at .\int.jl:252
[6] top-level scope at REPL[52]:1
julia> rem(1, 0)
ERROR: DivideError: integer division error
Stacktrace:
[1] rem(::Int64, ::Int64) at .\int.jl:261
[2] top-level scope at REPL[54]:1
浮点类型
下表列出来 Julia 支持的浮点类型:
| 类型 | 精度 | 比特数 |
|---|---|---|
| Float16 | 半精度 | 16 |
| Float32 | 单精度 | 32 |
| Float64 | 双精度 | 64 |
此外,对复数和有理数的完整支持是在这些原始数据类型之上建立起来的。
浮点数字面量格式表示如下,必要时可使用 E 来表示。
实例
julia> 1.0
1.0
julia> 1.
1.0
julia> 0.5
0.5
julia> .5
0.5
julia> -1.23
-1.23
julia> 1e10
1.0e10
julia> 2.5e-4
0.00025
注:
在科学计数法中,为了使公式简便,可以用带 E 的格式表示。例如 1.03乘10的8次方,可简写为 "1.03E+08" 的形式,其中 "E" 是 exponent(指数) 的缩写。
上面的结果都是 Float64 类型的值。使用 f 替代 e 可以得到 Float32 类型的字面量:
实例
julia> x = 0.5f0
0.5f0
julia> typeof(x)
Float32
julia> 2.5f-4
0.00025f0
数值可以很容易地转换为 Float32 类型:
julia> x = Float32(-1.5)
-1.5f0
julia> typeof(x)
Float32
也存在十六进制的浮点数字面量,但只适用于 Float64 类型的值。一般使用 p 前缀及以 2 为底的指数来表示:
实例
julia> 0x1p0
1.0
julia> 0x1.8p3
12.0
julia> x = 0x.4p-1
0.125
julia> typeof(x)
Float64
Julia 也支持半精度浮点数(Float16),但它们是使用 Float32 进行软件模拟实现的。
julia> sizeof(Float16(4.))
2
julia> 2*Float16(4.)
Float16(8.0)
下划线 _ 可用作数字分隔符:
实例
julia> 10_000, 0.000_000_005, 0xdead_beef, 0b1011_0010
(10000, 5.0e-9, 0xdeadbeef, 0xb2)
浮点数中的零
浮点数有两种零,正零和负零。它们相互相等但有着不同的二进制表示,可以使用 bitstring 函数来查看:
实例
julia> 0.0 == -0.0
true
julia> bitstring(0.0)
"0000000000000000000000000000000000000000000000000000000000000000"
julia> bitstring(-0.0)
"1000000000000000000000000000000000000000000000000000000000000000"
特殊的浮点值
有三种特定的标准浮点值不和实数轴上任何一点对应:
| Float16 | Float32 | Float64 | 名称 | 描述 |
|---|---|---|---|---|
| Inf16 | Inf32 | Inf | 正无穷 | 一个大于所有有限浮点数的数 |
| -Inf16 | -Inf32 | -Inf | 负无穷 | 一个小于所有有限浮点数的数 |
| NaN16 | NaN32 | NaN | 不是一个数 | 一个不和任何浮点值(包括自己)相等(==)的值 |
以下列举了一些浮点数的运算实例:
实例
julia> 1/Inf
0.0
julia> 1/0
Inf
julia> -5/0
-Inf
julia> 0.000001/0
Inf
julia> 0/0
NaN
julia> 500 + Inf
Inf
julia> 500 - Inf
-Inf
julia> Inf + Inf
Inf
julia> Inf - Inf
NaN
julia> Inf * Inf
Inf
julia> Inf / Inf
NaN
julia> 0 * Inf
NaN
julia> NaN == NaN
false
julia> NaN != NaN
true
julia> NaN < NaN
false
julia> NaN > NaN
false
我们还可以使用 typemin 和 typemax 函数:
实例
julia> (typemin(Float16),typemax(Float16))
(-Inf16, Inf16)
julia> (typemin(Float32),typemax(Float32))
(-Inf32, Inf32)
julia> (typemin(Float64),typemax(Float64))
(-Inf, Inf)
机器精度
大多数实数都无法用浮点数准确地表示,因此有必要知道两个相邻可表示的浮点数间的距离,它通常被叫做机器精度。
Julia 提供了 eps 函数,它可以给出 1.0 与下一个 Julia 能表示的浮点数之间的差值:
实例
julia> eps(Float32)
1.1920929f-7
julia> eps(Float64)
2.220446049250313e-16
julia> eps() # 与 eps(Float64) 相同
2.220446049250313e-16
这些值分别是 Float32 中的 2.0^-23 和 Float64 中的 2.0^-52。eps 函数也可以接受一个浮点值作为参数,然后给出这个值与下一个可表示的浮点数值之间的绝对差。也就是说,eps(x) 产生一个和 x 类型相同的值,并且 x + eps(x) 恰好是比 x 更大的下一个可表示的浮点值:
实例
julia> eps(1.0)
2.220446049250313e-16
julia> eps(1000.)
1.1368683772161603e-13
julia> eps(1e-27)
1.793662034335766e-43
julia> eps(0.0)
5.0e-324
两个相邻可表示的浮点数之间的距离并不是常数,数值越小,间距越小,数值越大,间距越大。换句话说,可表示的浮点数在实数轴上的零点附近最稠密,并沿着远离零点的方向以指数型的速度变得越来越稀疏。根据定义,eps(1.0) 与 eps(Float64) 相等,因为 1.0 是个 64 位浮点值。
Julia 也提供了 nextfloat 和 prevfloat 两个函数分别返回基于参数的下一个更大或更小的可表示的浮点数:
实例
julia> x = 1.25f0
1.25f0
julia> nextfloat(x)
1.2500001f0
julia> prevfloat(x)
1.2499999f0
julia> bitstring(prevfloat(x))
"00111111100111111111111111111111"
julia> bitstring(x)
"00111111101000000000000000000000"
julia> bitstring(nextfloat(x))
"00111111101000000000000000000001"
这个例子体现了一般原则,即相邻可表示的浮点数也有着相邻的二进制整数表示。
舍入模式
一个数如果没有精确的浮点表示,就必须被舍入到一个合适的可表示的值。
Julia 所使用的默认模式总是 RoundNearest,指舍入到最接近的可表示的值,这个被舍入的值会使用尽量少的有效位数。
实例
julia> BigFloat("1.510564889",2,RoundNearest)
1.5
julia> BigFloat("1.550564889",2,RoundNearest)
1.5
julia> BigFloat("1.560564889",2,RoundNearest)
1.5
0 和 1 的字面量
Julia 提供了 0 和 1 的字面量函数,可以返回特定类型或所给变量的类型。
| 函数 | 描述 |
|---|---|
| zero(x) | x 类型或变量 x 的类型的零字面量 |
| one(x) | x 类型或变量 x 的类型的一字面量 |
这些函数在数值比较中可以用来避免不必要的类型转换带来的开销。
例如:
实例
julia> zero(Float32)
0.0f0
julia> zero(1.0)
0.0
julia> one(Int32)
1
julia> one(BigFloat)
1.0
类型转换
类型转换是把变量从一种类型转换为另一种数据类型。例如,如果您想存储一个 float 类型的值到一个简单的整型中,您需要把 float 类型强制转换为 int 类型。您可以使用强制类型转换运算符来把值显式地从一种类型转换为另一种类型,如下所示:
Julia 支持三种数值转换,它们在处理不精确转换上有所不同。
第一种:
T(x) 或 convert(T,x)
以上都会把 x 转换为 T 类型。
- 如果 T 是浮点类型,转换的结果就是最近的可表示值, 可能会是正负无穷大。
- 如果 T 为整数类型,当 x 不能由 T 类型表示时,会抛出 InexactError。
第二种:
x % T 也可以将整数 x 转换为整型 T,与 x 模 2^n 的结果一致,其中 n 是 T 的位数。
第三种:
舍入函数接收一个 T 类型的可选参数。比如,round(Int,x) 是 Int(round(x)) 的简写版。
实例
julia> Int8(127)
127
julia> Int8(128)
ERROR: InexactError: trunc(Int8, 128)
Stacktrace:
[...]
julia> Int8(127.0)
127
julia> Int8(3.14)
ERROR: InexactError: Int8(3.14)
Stacktrace:
[...]
julia> Int8(128.0)
ERROR: InexactError: Int8(128.0)
Stacktrace:
[...]
julia> 127 % Int8
127
julia> 128 % Int8
-128
julia> round(Int8,127.4)
127
julia> round(Int8,127.6)
ERROR: InexactError: trunc(Int8, 128.0)
Stacktrace:
[...]
相关文章:

Julia 数据类型
在编程语言中,都有基本的数学运算和科学计算,它们常用的数据类型为整数和浮点数。 另外还有一个"字面量"的术语,字面量(literal)用于表达源代码中一个固定值的表示法(notation)&…...
01-基于SOA架构someip 开发-Linux开发环境搭建
前言:SOME/IP 是一个汽车的中间件解决方案,可用于控制消息。从一开始,它的设计就是为了完美地适应不同尺寸和不同操作系统的设备。这包括小型设备,如相机、AUTOSAR设备,以及头部单元或远程信息处理设备。同时还确保了S…...

历时半年!从外包到现在阿里网易25K,分享一下自己的涨薪经验
前言 首先自我介绍一下,本人普通一本毕业,年初被老东家裁员干掉了,之后一直住在朋友那混吃等死,转折是今年年后,二月初的时候和大佬吃了个饭,觉得自己不能这样下去了,拿着某大佬给我的面试资料…...

支付系统中的设计模式04:改进的策略与外观模式
随着业务越做越大,交易量大了,老板觉得可以用一些变相的方法增加一些收入了,同时也有利于用户,做到双赢。这很好理解,“往地上戳一棍子都能冒出油来”,谁能扛得住这种诱惑呢? 于是,老板就提了这样的需求: 支付系统需要根据不同的结算模式,返利给账户: 1、选择T+1结算…...
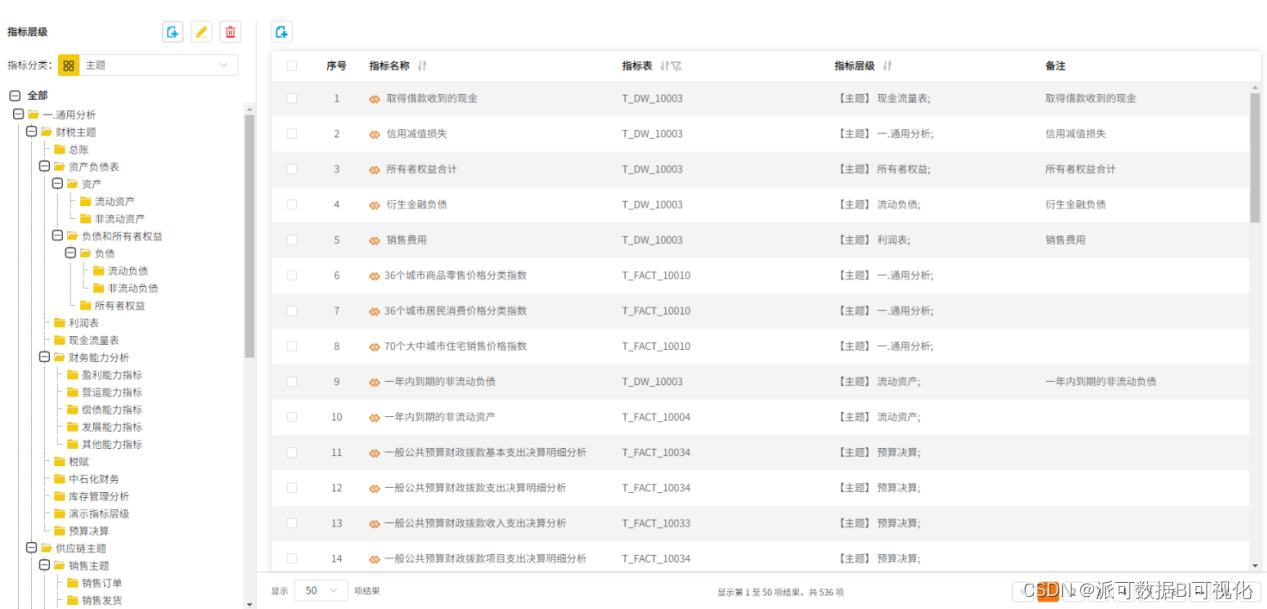
关于数据分析和数据指标,企业还需要做什么?
数据虽然已经成为了各行各业对未来的共识,也切实成为了各领域企业的重要资产。但真正谈到发挥数据的价值,就必须从规模庞大的数据中找出需求的数据,然后进行利用。这个过程光是想想就知道很麻烦,更别提很多数据都是经常会用到的&a…...

jvm之垃圾回收器
分类 按线程 串行并行工作模式 并发式独占式碎片处理方式 压缩式非压缩式工作内存空间 年轻代老年代 评估GC的性能指标 吞吐量:运行用户代码的时间占总运行时间的比例暂停时间:执行垃圾收集时,程序的工作线程被暂停的时间内存占用: java堆区…...

【c++】类和对象7—继承
文章目录关于继承继承与非继承的对比继承方式继承中的对象模型继承中的构造和析构顺序继承同名成员处理方式继承同名静态成员处理方式多继承语法菱形继承关于继承 我们发现,定义一些类时,下级别的成员处理拥有上一级的共性,还有自己的特性。 …...

vue实现预览、下载和打印后端返回的pdf文件流
需求:后端返回pdf文件流,前端能够预览、下载打印。 后端返回的文件流部分截图 需要实现的效果图 前面第1步只是为了展示后台返回数据流,完成功能的时候,不需要调用接口的,只需要利用调用接口的url。 实现步骤&am…...

【Android视频号④ 问题总结】
这节坑比较多~ 差点没把我给整死!!! 环境介绍 首先我调试都是root过的真机,但是生产环境都是没有Root的云机,属于自己改的Rom框架也不是XP或LSP 是技术人员利用Xposed源码改的框架 问题&解决 模块源码更改 这…...
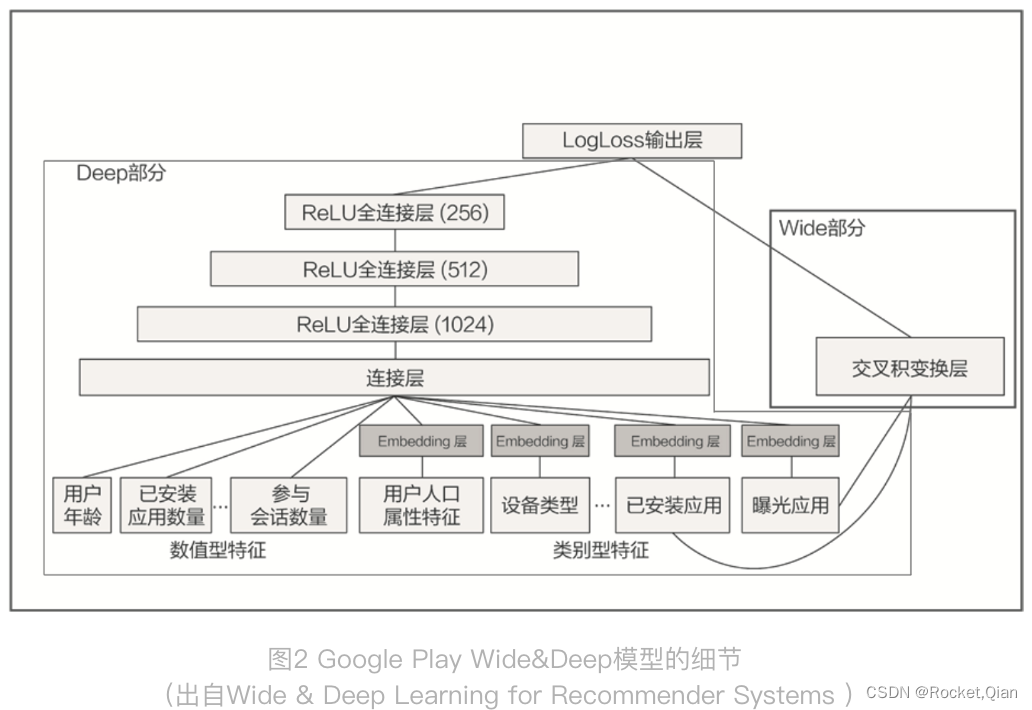
推荐算法—widedeep原理知识总结代码实现
wide&deep原理知识总结代码实现1. Wide&Deep 模型的结构1.1 模型的记忆能力1.2 模型的泛化能力2. Wide&Deep 模型的应用场景3. Wide&Deep 模型的代码实现3.1 tensorflow实现3.2 pytorch实现今天,总结一个在业界有着巨大影响力的推荐模型,…...
PHP面向对象03:命名空间
PHP面向对象03:命名空间一、命名空间基础二、子空间三、命名空间访问1. 非限定名称2. 限定名称3. 完全限定名称四、全局空间五、命名空间应用六、命名空间引入一、命名空间基础 namespace,是指人为的将内存进行分隔,让不同内存区域的同名结构…...
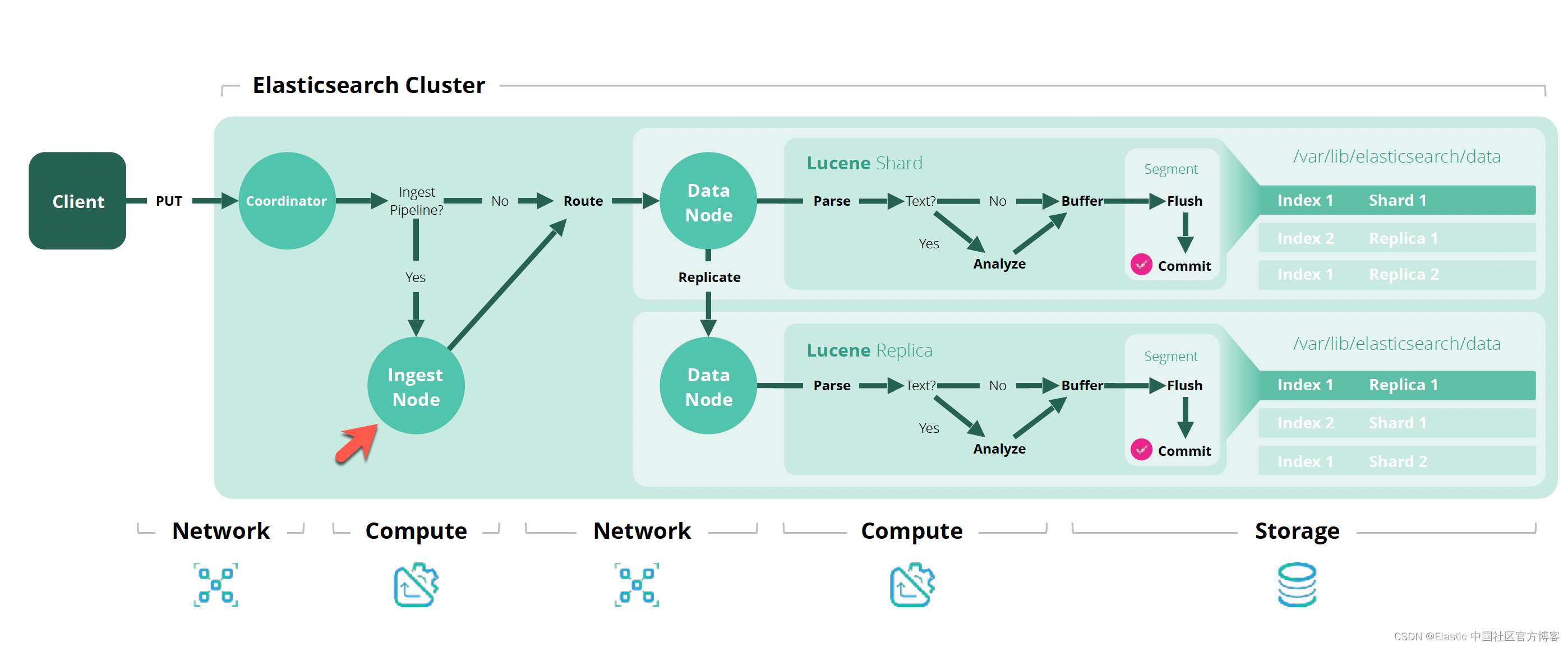
Elasticsearch:使用 pipelines 路由文档到想要的 Elasticsearch 索引中去
路由文件 当应用程序需要向 Elasticsearch 添加文档时,它们首先要知道目标索引是什么。在很多的应用案例中,特别是针对时序数据,我们想把每个月的数据写入到一个特定的索引中。一方面便于管理索引,另外一方面在将来搜索的时候可以…...

前端开发常用的18个JavaScript框架和库
JavaScript 可以说是最流行的编程语言之一,也是Web 开发人员必须学习的 3 种语言之一,JavaScript 几乎可以做任何事情,更可以在包括物联网在内的多个平台和设备上运行。在WebGL库和SVG/Canvas元素的支持下,JavaScript变得惊人的强…...

理解、总结重点知识
一、常见的数据结构 1、数组结构 数组结构: 存储区间连续、内存占用严重、空间复杂度大 优点:随机读取和修改效率高,原因是数组是连续的(随机访问性强,查找速度快)缺点:插入和删除数据效率低&a…...

记一次从文件备份泄露到主机上线
前言 记录下某个测试项目中,通过一个文件备份泄露到主机上线的过程。 文件备份泄露 对于测试的第一项当然是弱口令,bp跑了一通词典,无果。目录又爆破了一通,发现一个web.rar可通,赶紧下载看看,如下图所示…...

8年测开经验面试28K公司后,吐血整理出1000道高频面试题和答案
1、python的数据类型有哪些 答:Python基本数据类型一般分为:数字、字符串、列表、元组、字典、集合这六种基本数据类型。 浮点型、复数类型、布尔型(布尔型就是只有两个值的整型)、这几种数字类型。列表、元组、字符串都是序列。 2、列表和元组的区别 答…...

Linux 基础知识之权限管理
目录一、权限的认识二、用户切换三、文件权限1.三类文件访问者2.文件权限类型3.文件访问权限4.文件权限值表示一、权限的认识 权限是对用户所能进行的操作的限制,如果不对用户作出限制,那么碰到恶意用户,就会损害其他用户的利益。 Linux是多用…...

百度LAC分词
对应数据的链接放这里了 import pandas as pd from util.logger import Log import os from util.data_dir import root_dir from LAC import LAC os_file_name os.path.split(os.path.realpath(__file__))[-1]# 加载LAC模型 lac LAC(mode"lac") # 载入自定义词典 …...

软件测试面试题 —— 整理与解析(1)
😏作者简介:博主是一位测试管理者,同时也是一名对外企业兼职讲师。 📡主页地址:🌎【Austin_zhai】🌏 🙆目的与景愿:旨在于能帮助更多的测试行业人员提升软硬技能…...

深入浅出C++ ——红黑树模拟实现STL中的set与map
文章目录一、红黑树二、用泛型红黑树模拟实现set三、用泛型红黑树模拟实现map一、红黑树 红黑树作为set和map的底层容器,既要实现插入key又要实现插入pair,所以做了稍许的改动,使其成为一颗泛型结构的红黑树,通过不同的实例化参数…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
