[python 刷题] 49 Group Anagrams
[python 刷题] 49 Group Anagrams
题目:
Given an array of strings
strs, group the anagrams together. You can return the answer in any order.An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
这里 Anagram 的定义就是可以通过重新排序获得的单词,如 cat 可以获得 act 这种,所以这道题需要按需将所有 Anagram 组合在一起,如:
["eat","tea","tan","ate","nat","bat"] 中包含
{'a': 1, 'e': 1, 't': 1}为 key 的[eat, tea, ate]{'b': 1, 'a': 1, 't': 1}为 key 的[bat]{'t': 1, 'a': 1, 'n': 1}为一组的[tan, nat]
所以,最终的答案就是 [["bat"],["nat","tan"],["ate","eat","tea"]]
我最初的写法是:
class Solution:def groupAnagrams(self, strs: List[str]) -> List[List[str]]:# if no list, return emptyif len(strs) == 0:return strsana_dict = {}for str in strs:key = {}for c in str:key[c] = key.get(c, 0) + 1frozen_key = frozenset(key.items())if frozen_key in ana_dict:ana_dict[frozen_key].append(str)else:ana_dict[frozen_key] = [str]res = []for _, value in ana_dict.items():res.append(value)return res
这个写法的逻辑为:
- 便利每一个 key,将其转换为对应的 dict
- 因为 dict 可变(mutable),python 的 dict 要求 key 不可变,因此将其转化为 immutable 的
frozenset - 遍历 dict 生成最终结果
这是一个可以实行的方法,大 O 是 O ( n × k ) O(n \times k) O(n×k),其中 n n n 为数组的长度, k k k 为字符串的长度
随后我又看了一下别人是怎么写的,然后发现了更妙的两个写法:
class Solution:def groupAnagrams(self, strs: List[str]) -> List[List[str]]:# if no list, return emptyif len(strs) == 0:return strsana_dict = {}for str in strs:key = ''.join(sorted(list(str)))ana_dict[key] = ana_dict.get(key, [])ana_dict[key].append(str)res = []for _, value in ana_dict.items():res.append(value)return res
这个就不把遍历的 str 转换成 dict,而是直接通过排序的方式获得 Anagram,理论上来说这个写法的时间复杂度为 O ( n × k l o g ( k ) ) O(n \times k log(k)) O(n×klog(k)),不过我实际提交了几次,发现 leetcode 上这个写法的平均用时比第一个写法要短,可能有三个原因:
- dict 转 frozenset 太耗时了
- python 内部对 sort 的优化
- leetcode 的案例比较极端
第二个写法更妙一些,它最终的时间复杂度还是 O ( n × k ) O(n \times k) O(n×k),不过写法更简洁:
class Solution:def groupAnagrams(self, strs: List[str]) -> List[List[str]]:ans = collections.defaultdict(list)for str in strs:count = [0] * 26for c in str:count[ord(c) - ord('a')] += 1ans[tuple(count)].append(str)return ans.values()
这里主要用了一些比较妙的点:
-
使用了
collections.defaultdictcollections.defaultdict和 dict 主要的区别就在于,前者当遇到当前 dict 中不存在的 key,会使用提供的默认值,而 dict 就会直接报错以本题为例,
ans = collections.defaultdict(list)代表着所有 key 的默认初始值为[],也就可以直接使用append方法 -
与其使用 dict 去创建 k-v 对,不如直接使用 array,毕竟英文就 26 个字母
-
没有
frozenset去创建不可变的 key,而是使用了 tuple对于数量比较小——这里就 26 个字母——的 iterable 来说,tuple 一般来说会比 frozenset 快一些
-
直接使用内置的
values()进行返回,而没有做一个新的迭代
当然,实际运行上,这个跑法还是比用 sort 的要慢一点,但是比我之前写的那个方法要快一点点,不过写法则是干净很多
相关文章:

[python 刷题] 49 Group Anagrams
[python 刷题] 49 Group Anagrams 题目: Given an array of strings strs, group the anagrams together. You can return the answer in any order. An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically…...
vue+element plus 使用table组件,清空用户的选择项
<el-table ref"tableRef"> .... </el-table> <script lang"ts" setup> import { onMounted, reactive, ref, nextTick } from vue const clearBtn () > {console.log(清空用户的选择项)tableRef.value.clearSelection() } </scr…...

改写软件-怎么选择改写软件
什么是改写软件?改写软件是基于自然语言处理技术的工具,它们可以分析一段文字,并将其重新表达,以保持原始意义,但使用不同的词汇和结构。这种技术可用于减少内容的重复,增加多样性,或者简化复杂…...
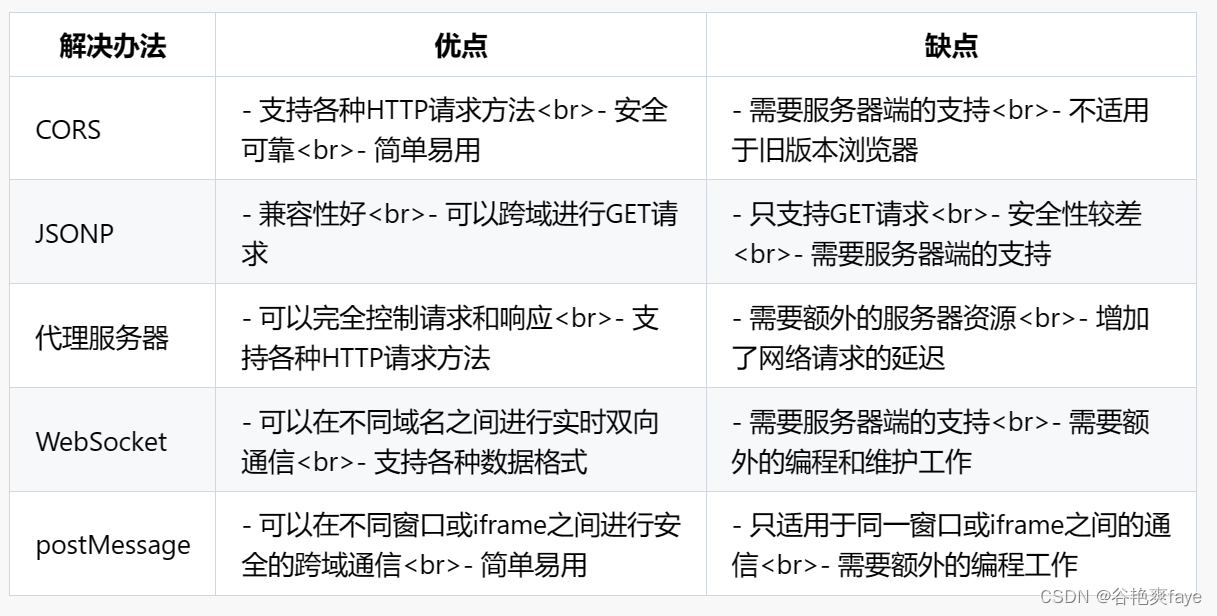
gateway之跨域处理
文章目录 什么是跨域跨域带来的问题 gateway解决跨域解决跨域的其他方式比较代码示例 总结提升 什么是跨域 跨域(Cross-Origin)是指在浏览器中,当一个Web应用程序试图访问与其所属页面不同的源(origin)的资源时&#…...
uniapp 实现不同用户展示不同的tabbar(底部导航栏)
一、背景 最近在做一个uniapp开发的小程序遇到一个需求,希望不同用户登录后展示不同的tabbar页面,但是uniapp项目中的pages.json是只有一个list数组的,并且是不能写成动态效果,为了实现这个需求,便自定义了tabbar组件 …...

线性归一化是什么,用python实现数据的线性归一化
线性归一化(Linear Normalization)是一种常见的数据预处理方法,也被称为 Min-Max 归一化。它通过对原始数据进行线性变换,将其缩放到特定的范围内,常用的是将数据缩放到 [0, 1] 或 [-1, 1] 范围内。 具体来说ÿ…...
超级好用绘图工具(Draw.io+Github)
超级好用绘图工具(Draw.ioGithub) 方案简介 绘图工具:Draw.io 存储方式: Github 1 Draw.io 1.2 简介 是一款免费开源的在线流程图绘制软件,可以用于创建流程图、组织结构图、网络图、UML图等各种类型的图表。…...
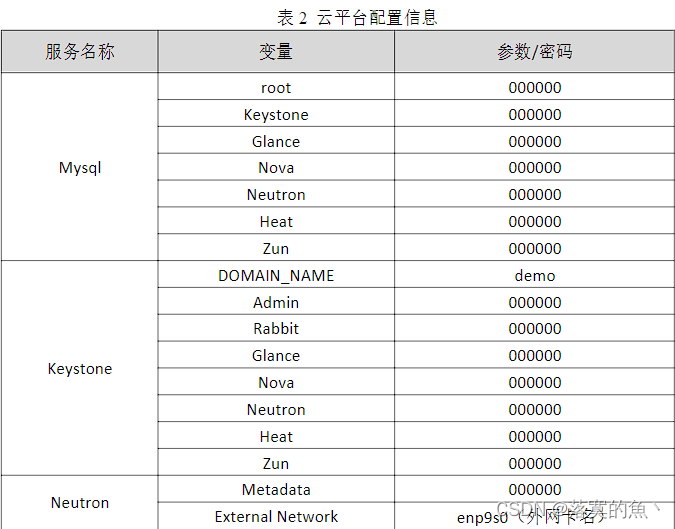
全国职业技能大赛云计算--高职组赛题卷③(私有云)
全国职业技能大赛云计算--高职组赛题卷③(私有云) 第一场次题目:OpenStack平台部署与运维任务1 基础运维任务(5分)任务2 OpenStack搭建任务(15分)任务3 OpenStack云平台运维(15分&am…...
)
Redis SCAN命令操作实战(详细)
目录 SCAN 介绍 SCAN 命令基本用法 MATCH 选项用法 COUNT 选项用法 TYPE 选项用法 补充 并发执行多个迭代 中途停止迭代 使用错误的游标进行增量式迭代 迭代终结的保证 SCAN 介绍 SCAN cursor [MATCH pattern] [COUNT count][TYPE type]:SCAN 命令及其相…...
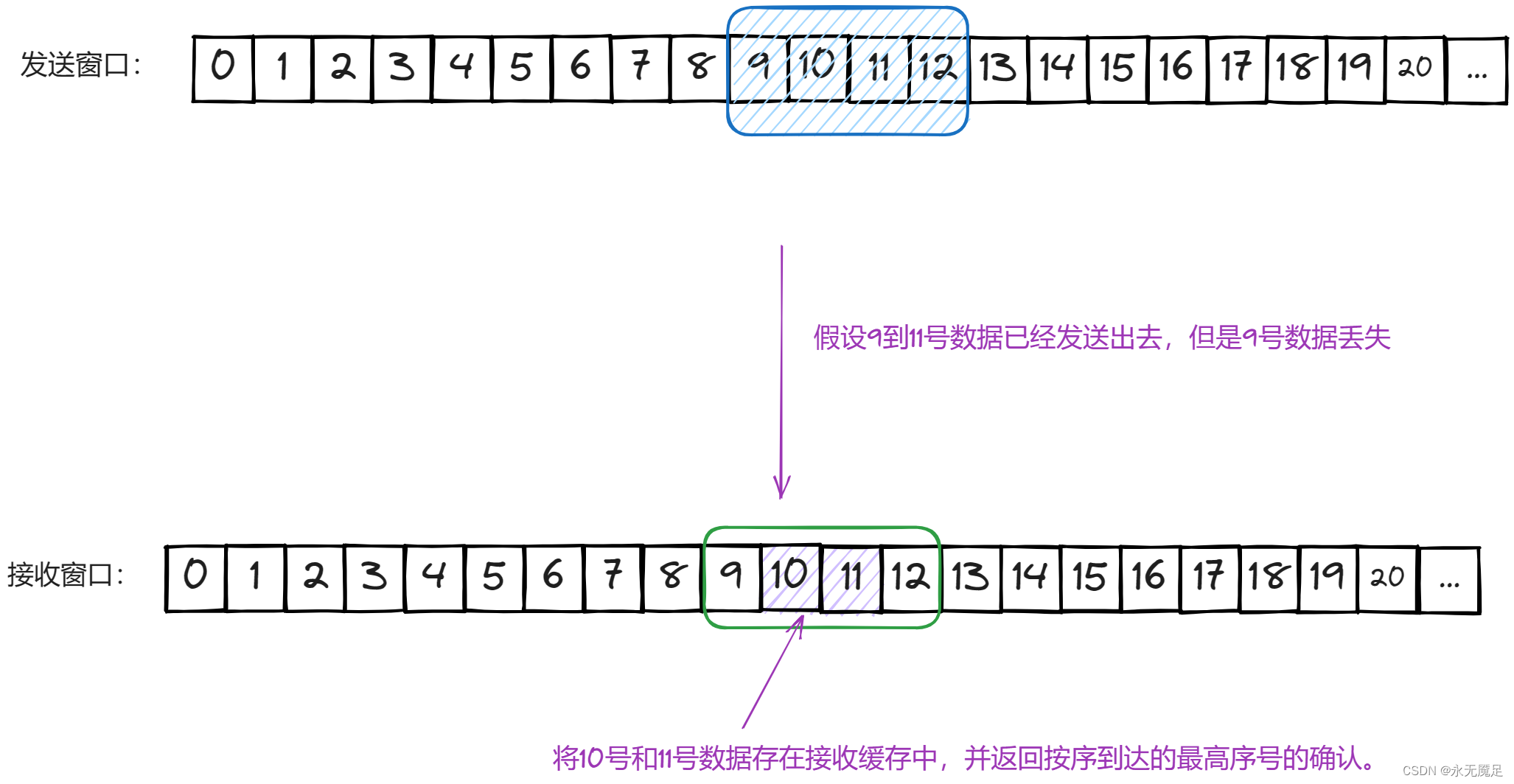
计网第五章(运输层)(六)(TCP可靠传输的实现)
目录 一、基本概述 二、具体实现 1.前后沿: 2.利用指针描述发送窗口的状态 3.有差错情况 之前在数据链路层时已经讨论过可靠传输(计网第三章(数据链路层)(二)(可靠传输)&#x…...
酒店外卖小程序商城的作用是什么
随着线上餐品销售属性增强,传统酒店除了承接到店客户,外送也成为生意的一部分,但传统打电话、微信发送的方式无法实现餐品全面呈现和客户随时订购需求,在配送方面也无法规范化。 除此之外,还需要完善营销、会员管理、…...

居家养老一键通的功能
居家养老一键通的功能 居家养老一键通是指为老年人提供全方位的居家养老服务的平台或系统。它通过整合各种资源和服务,为老年人提供便捷、安全、舒适的居家养老环境,帮助他们解决生活中的各种难题。 居家养老一键通的功能通常包括以下几个方面ÿ…...
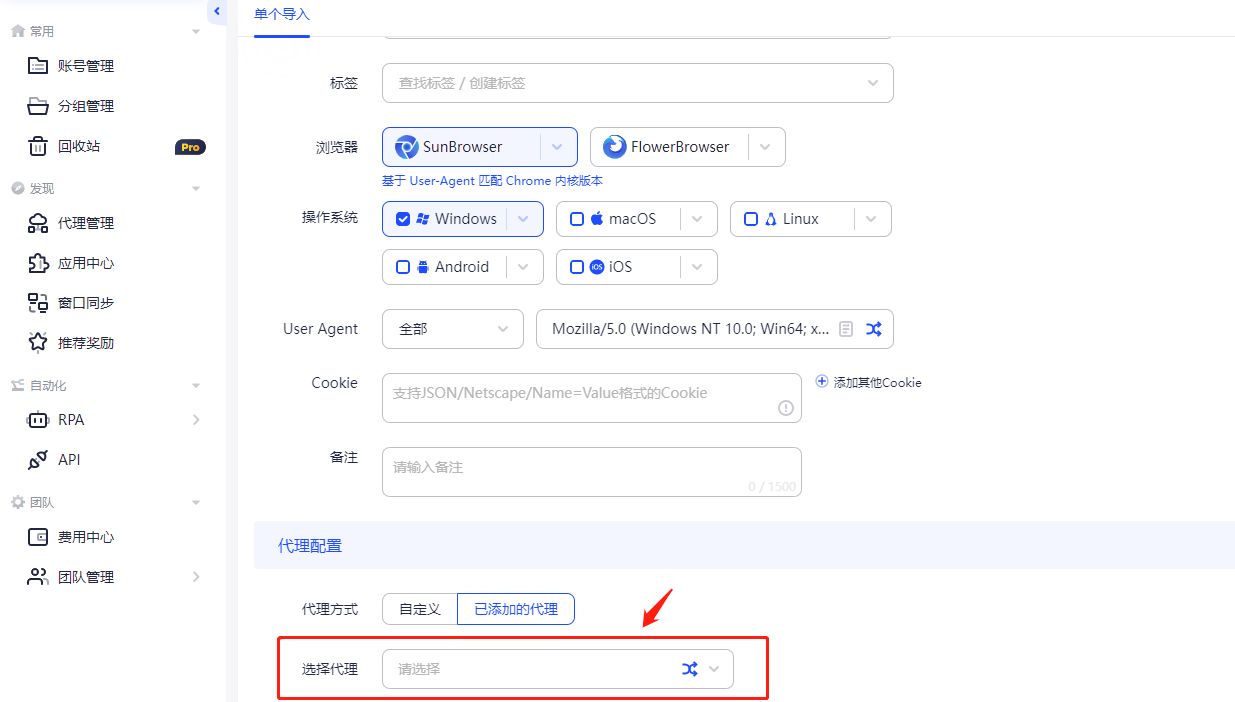
海外代理IP是什么?如何使用?
一、海外代理IP是什么? 首先,代理服务器是在用户和互联网之间提供网关的系统或路由器。它是一个服务器,被称为“中介”,因为它位于最终用户和他们在线访问的网页之间。 海外IP代理是就是指从海外地区获取的IP地址,用…...

mmdetection v3避坑
命令: python tools/test.py projects/DiffusionDet/configs/diffusiondet_r50_fpn_500-proposals_1-step_crop-ms-480-800-450k_coco.py /data/zhangrui/mmdetection-master/checkpoints/diffusiondet_r50_fpn_500-proposals_1-step_crop-ms-480-800-450k_coco_202…...

备份服务器数据库并保存到Git仓库
备份项目及数据库脚本 #!/bin/bash # MySQL数据库信息 DB_HOST"localhost" DB_USER"root" DB_PASS"************" DB_NAME"my-space" # 导出文件目录 EXPORT_PATH"/home/MySpace/mysql" # 获取当前时间并格式…...
尚硅谷wepack课程学习笔记
为什么需要使用打包工具? 开发时使用的框架、es6 语法 、less 等浏览器无法识别。 需要经过编译成浏览器能识别的css、js才可以运行。 打包工具可以帮我们编译,号可以做代码压缩、兼容处理、性能优化。 常见的打包工具有什么? vite、webpac…...

c++模版元编程-可变参数模版
在 C 中,我们可以使用模板参数包(Template Parameter Pack)和展开表达式(Expanding Expression)来定义可变参数模板。 模板参数包 模板参数包是一种特殊的语法,用于表示接受多个模板类型参数或非类型参数…...

pcl--第十节 点云曲面重建
曲面重建技术在逆向工程、数据可视化、机器视觉、虚拟现实、医疗技术等领域中得到了广泛的应用 。 例如,在汽车、航空等工业领域中,复杂外形产品的设计仍需要根据手工模型,采用逆向工程的手段建立产品的数字化模型,根据测量数据建…...

【力扣-每日一题】2560. 打家劫舍 IV
class Solution { public:bool check(vector<int> &nums,int max_num,int k){//只需要计算可以偷的房间。在满足最大值为max_num下时,能偷的最多的房间,与k值比较//如果大于K,说明max_num还可以缩小//如果小于看,说明ma…...
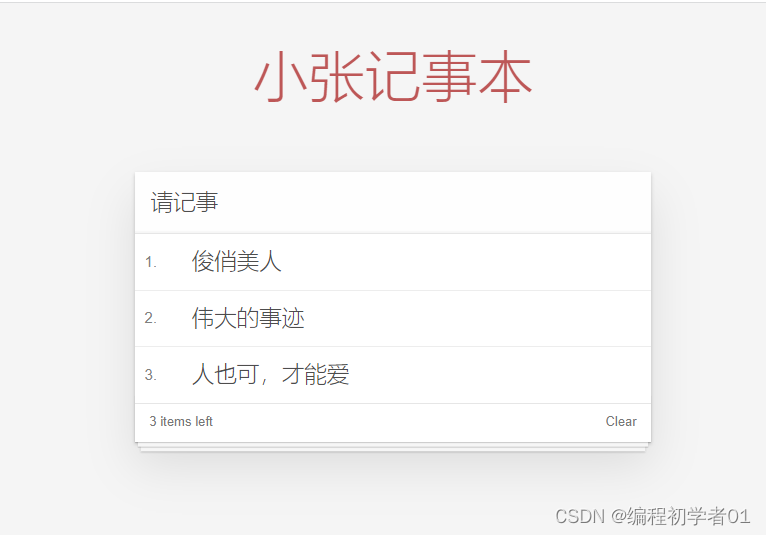
vue简单案例----小张记事本
小张记事本 具体效果如图所示,这里就简单展示,还有很多不足的地方,希望大家可以对这个小项目进行改进,话不多说可以参考下面的代码 源代码如下 <html lang"en"><head><meta charset"UTF-8"…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...
