uniapp 离线打包 plus.runtime.install 安装页面不弹起
uniapp 离线打包 plus.runtime.install 安装页面不弹起
updateVersion(webview : any, eventTitle : string, eventContent : string) {const loading = plus.nativeUI.showWaiting('准备下载');var dtask = plus.downloader.createDownload(eventContent,{method: 'GET',timeout: 5000,},(d, status) => {if (status === 200) {console.log('下载成功正在安装: ' + d.filename);plus.runtime.install(d.filename!);} else {plus.nativeUI.alert('安装失败,请稍候重试: ' + status);}});dtask.addEventListener('statechanged', (task) => {switch (task.state) {case 1:loading.setTitle('正在下载');break;case 2:loading.setTitle('已连接到服务器');break;case 3:const pr = Math.floor(((task.downloadedSize || 0) / (task.totalSize || 0)) * 100);loading.setTitle(`正在下载 ${pr} %`);break;case 4:plus.nativeUI.closeWaiting();break;}});dtask.start();}
贴一下下载代码;
云打包正常可以调起安装页面,离线打包无法调起;
最终原因:
解决 上架 google play 审核报 DCloud SDK 包含从未知来源下载或安装应用 的问题
从官方SDK中引入这个arr文件
Android-SDK@3.8.12.81924_20230817\SDK\libs\install-apk-release.aar
吐槽:文档确实有点乱
相关文章:

uniapp 离线打包 plus.runtime.install 安装页面不弹起
uniapp 离线打包 plus.runtime.install 安装页面不弹起 updateVersion(webview : any, eventTitle : string, eventContent : string) {const loading plus.nativeUI.showWaiting(准备下载);var dtask plus.downloader.createDownload(eventContent,{method: GET,timeout: 5…...

Docker 自动化部署(保姆级教程)
Docker 自动化部署 1. jenkins 介绍1.1 参考链接:1.2 jenkins 概述1.3 jenkins部署项目的流程 2. jenkins 安装2.1 基于docker 镜像2.2 启动 jenkins 后端服务2.3 登录 jenkins 服务后端 3. jenkins自动化部署开始3.1 下载需要的插件3.2 创建任务3.2.1 描述3.2.2 配…...
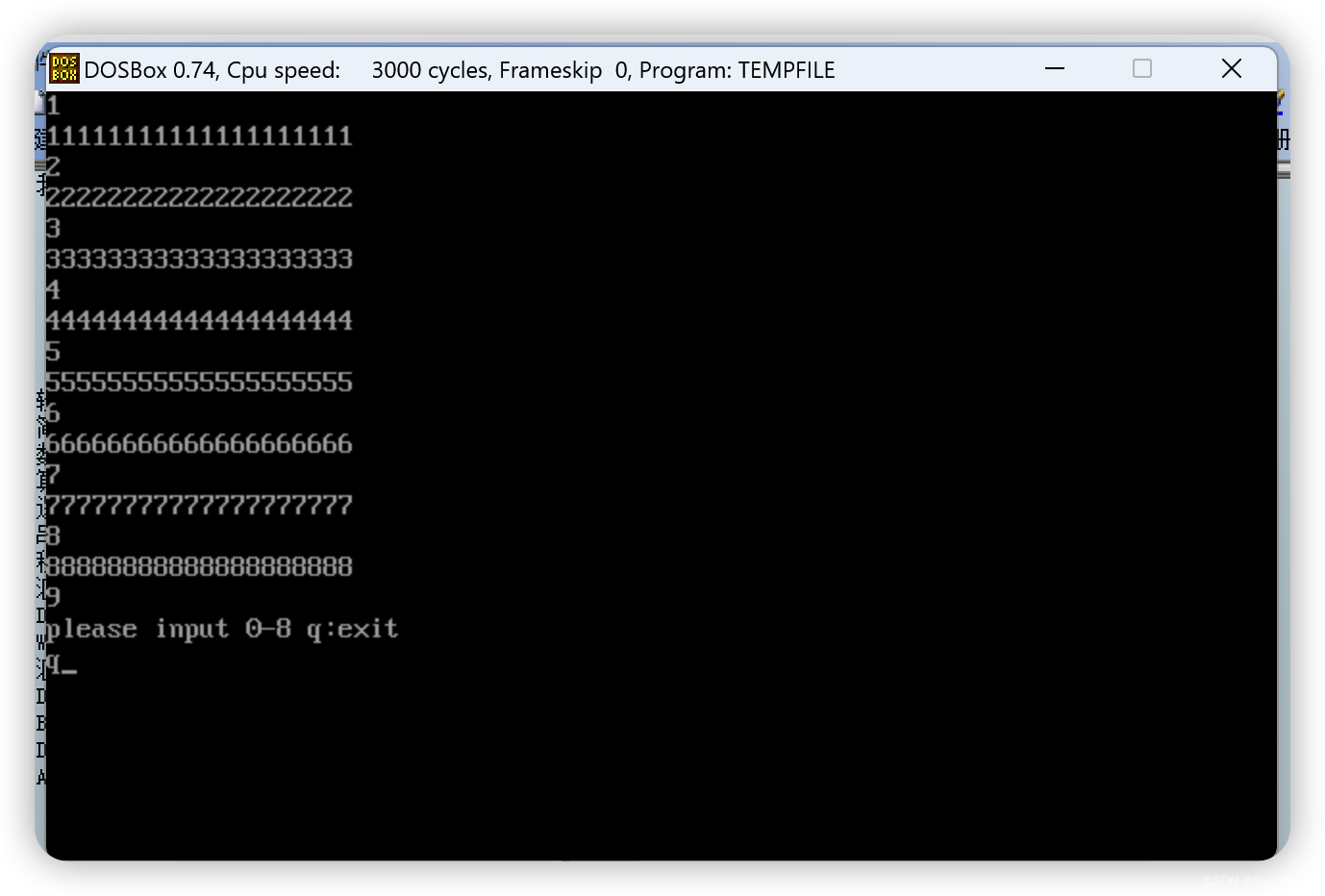
北工大汇编题——分支程序设计
题目要求 信息检素程序设计:在数据区,有9个不同的信息,编号 0-8,每个信息包括20 个字符。从键盘接收 0-8 之间的一个编号,然后再屏幕上显示出相应编号的信息内容,按“q”键退出 完整代码 DATAS SEGMENTn0…...
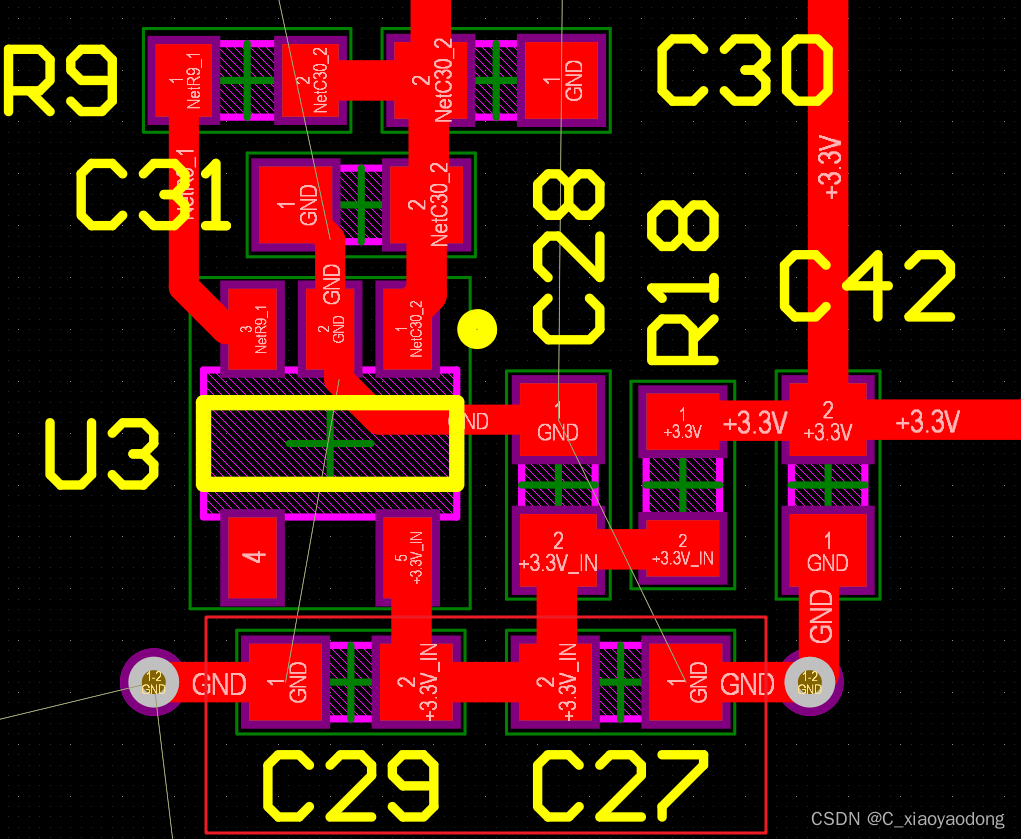
贴片电容耐压值选取和特性(包含实际电路和PCB)
一、一般电容的特性 ①容值大的电容,一般通低频率; ②容值小的电容,一般通高频率。 注:详细请看这位博主的篇文章: 大电容为什么虑低频小电容为什么又虑高频?(个人整理) 二、贴片电容的耐压选取 ①贴片电容有2…...
)
【云原生】kubernetes中pod(进阶)
目录 一、资源限制 业务cpu 内存 1.1CPU 资源单位 1.2 内存 资源单位 示例1 示例2: 二、健康检查:又称为探针(Probe) 2.1探针的三种规则 2.2 Probe支持三种检查方法 2.3示例 示例1:exec方式 示例3…...

Cesium 问题:获取高度值,高度值又是相对于谁来说的
文章目录 问题分析 问题 今天在开发中,甲方提出一个这样的问题,你的高度是怎么算出来的,对此,我只知道使用并不知道怎么来的,因此特意查了一番资料,希望帮助到大家 分析 在 Cesium 中,我们可以使…...
第三、四、五场面试
第三场 共享屏幕做题(三道简单题) 替换空格成%20(双指针) 删除升序链表中的重复元素(指针)有效的括号(栈) 第四场、第五场 自我介绍 项目拷打 整个项目架构rpc模块的情况分析的数…...
力扣-290.单词规律
Idea 先建立一个hashmap,记录s串中的每个单词以及对应的下标再建立一个hashmap,记录pattern串中相同字母以及对应的下标遍历pattern串时,遇到不同字母存到pat表中,同时将下标对应的s中的单词存入到查重test集中,因为如…...

常见限流算法学习
文章目录 常见限流算法学习前言限流算法基本介绍固定窗口计数器限流算法计数器限流算法相关介绍计数器限流算法的实现(基于共享变量)计数器限流算法的实现(基于Redis) 滑动窗口计数器算法滑动时间窗口算法相关介绍介绍滑动时间窗口…...

JS面试相关
深拷贝、浅拷贝、递归、优化 扁平化 柯里化 this指向原型 继承 call、apply、bind js取整的方法,parseInt第二个参数是什么 forEach和map有什么区别,使用场景? 内存泄漏的场景 原型链原型 严格模式 Js中for in 和for of的区别 slice、splice、…...
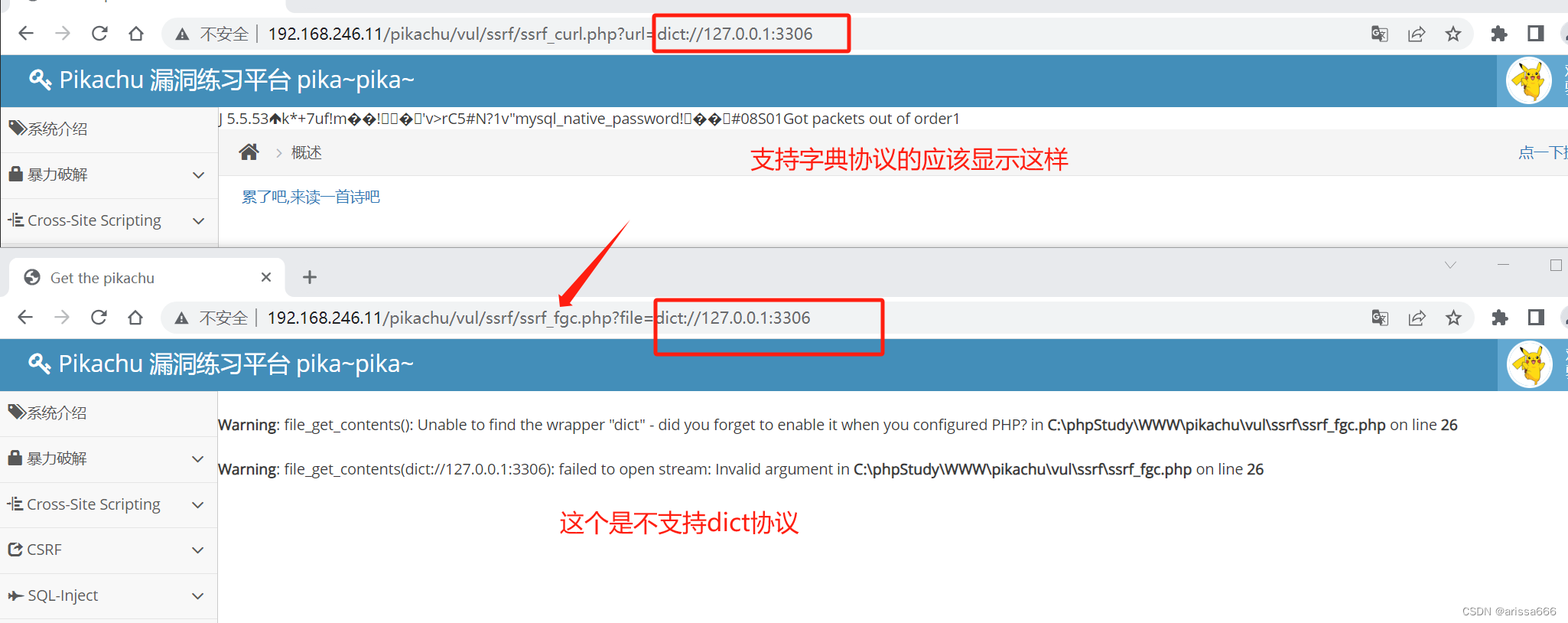
SSRF漏洞
Server-Side Request Forgery:服务器端请求伪造 目标:网站的内部系统 形成的原因 攻击者构造形成由服务器端发起请求的译者安全漏洞。 由于服务端提供了从其他服务器应用获取数据的功能,且没有对目标地址做过滤与限制。比如从指定URL地址获取网页文本内…...
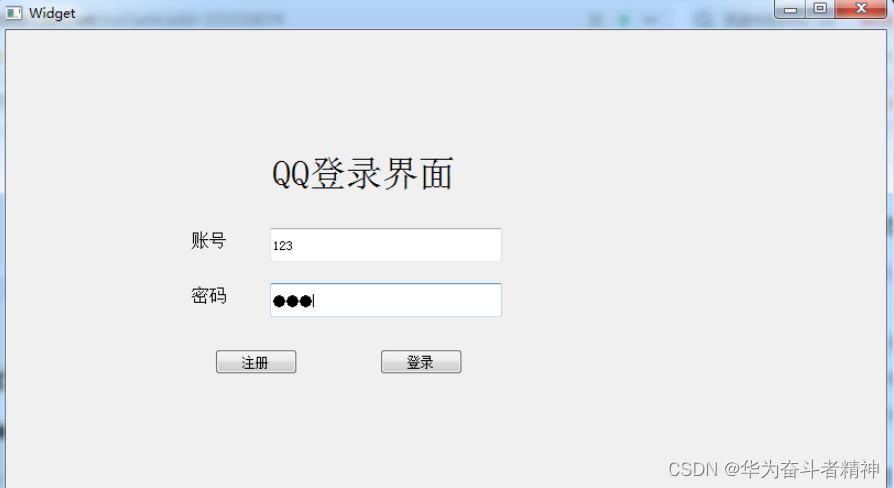
Qt5开发及实例V2.0-第十八章-Qt-MyselfQQ实例
Qt5开发及实例V2.0-第十八章-Qt-MyselfQQ实例 第18章-Qt MyselfQQ18.1 概述18.2 、发送文件18.3 、接收文件18.4 、保证传输的安全和稳定18.5 、总结 本章相关例程源码下载1.Qt5开发及实例_CH1801.rar 下载 第18章-Qt MyselfQQ 18.1 概述 MyselfQQ是一个基于Qt5框架开发的轻量…...

当下IT测试技术员的求职困境
从去年被裁到现在,自由职业的我已经有一年没有按部就班打卡上班了。期间也面试了一些岗位,有首轮就挂的,也有顺利到谈薪阶段最后拿了offer的,不过最后选择了拒绝。 基于自己近一年的面试求职经历,我想聊聊当下大家在求…...

MR混合现实情景实训教学
MR混合现实技术是一种将虚拟现实与现实场景相融合的创新技术,可以广泛应用于各个领域。其中,混合现实情景实训教学是MR技术的一个重要应用场景。 在医学专业方面,医学生常常需要通过实际操作来提升自己的技能水平,然而传统的实训方…...

嵌入式C++总结
1、new delete与malloc free区别 new delete是运算符,malloc free是函数。 前者不需要传入大小,后者需要。 前者会调用构造、析构函数,后者不会。 前者不需要强制转换,后者需要。 2、智能指针 智能指针是避免忘记释放动态申请对象…...
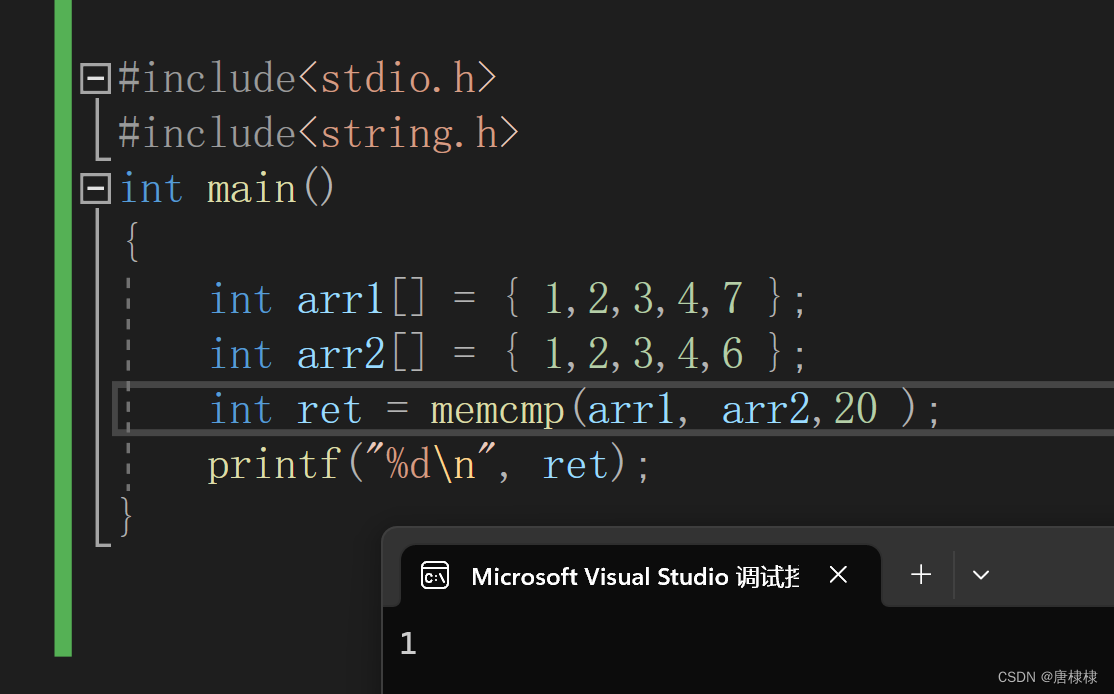
C语言之内存函数篇(3)
目录 memcpy memcpy的使用 memcpy的模拟实现 NO1. NO2. memcpy可否实现重叠空间的拷贝 my_memcpy memcpy memmove memmove memmove 分析 代码 memset memset的使用 memcmp memcmp的使用 <0 0 >0 今天我们继续介绍几个重要的内存操作函数。&…...

java面试题-学成在线项目
1、详细说说你的项目吧 从以下几个方面进行项目介绍: 1、项目的背景,包括:是自研还是外包、什么业务、服务的客户群是谁、谁去运营等问题。 2、项目的业务流程 3、项目的功能模块 4、项目的技术架构 5、个人工作职责 6、个人负责模块的详细说…...

ViewBinding——Android之视图绑定
高版本的gradle不再支持 kotlin-android-extensions插件,因此view的绑定方式也有所改变。 1.启用视图绑定 android {...viewBinding {enabled true}} 如果想在生成绑定类时忽略某个布局文件,请将 tools:viewBindingIgnore"true" 属性添加到…...

vue学习-04vue的props配置项和mixin混入
今天仍然就是敲vue的一个demo,vue的props配置项和mixin混入 props配置项 Vue.js 中的 props 是用于在父组件向子组件传递数据的配置项。通过 props,你可以将父组件中的数据传递给子组件,并在子组件中使用这些数据。以下是关于 props 配置项…...
九、多项式朴素贝叶斯算法(Multinomial NB,Multinomial Naive Bayes)(有监督学习)
Multinomial Naive Bayes:用于多项式模型的Naive Bayes分类器 一、算法思路 多项式Naive Bayes分类器适用于离散特征分类(如文本分类中的字数) 多叉分布通常需要整数特征计数 不过,在实际应用中,分数计数(…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...
