使用自功率谱、互功率谱估计滤波器幅频特性
这段时间终于对工程中的随机信号的一般处理方式有点头绪了,功率谱密度估计是十分重要的方式之一,仍需继续深入细化相关内容。
示例:使用自功率谱、互功率谱估计滤波器幅频特性,自己实现 & Matlab自带函数实现。
clc;clear;close all;
fs = 44100;
t = 0:1/fs:1-1/fs;
in = randn(size(t));winlen = 1024;
overlap = winlen/2;% 滤波
order = 1; % 滤波器阶数高后,则曲线不太平滑
fc = 1200;
[b,a] = butter(order, fc/(fs/2), 'low');
out = filter(b, a, in);%% 自己实现cpsd、pwelch。整体思路与上周相同,但将功率谱密度估计方法由 相关法 改为 直接法
segments_i = buffer(in, winlen, overlap, "nodelay"); % 存放输入信号的分段交叠
segments_o = buffer(out, winlen, overlap, "nodelay"); % 存放输出信号的分段交叠
numSegments = size(segments_i, 2); % 分段数wd = hanning(winlen);spectrum_Pxx = zeros(winlen/2+1,numSegments); % 存放每段估计的自功率谱密度
spectrum_Pxy = zeros(winlen/2+1,numSegments); % 存放每段估计的互功率谱密度for i = 1:numSegments % 分段估计% 估计输入信号自功率谱密度in_fft = fft(segments_i(:,i).*wd);N = length(in_fft);P1 = abs(in_fft/N);P2 = P1(1:floor(N/2)+1);P2(2:end-1) = 2*P2(2:end-1);Pxx_ = P2.^2/(N*fs); % 估计输入、输出信号互功率谱密度out_fft = fft(segments_o(:,i).*wd);P3 = abs(out_fft/N);P4 = P3(1:floor(N/2)+1);P4(2:end-1) = 2*P4(2:end-1);Pxy_ = P4 .* conj(P2) / (N*fs);% 每段的功率谱密度存起来spectrum_Pxx(:,i) = Pxx_;spectrum_Pxy(:,i) = Pxy_;endf = fs*(0:N/2)/N;% 计算均值
spectrumAvg_Pxx = mean(spectrum_Pxx, 2);
spectrumAvg_Pxy = mean(spectrum_Pxy, 2);H2 = abs(spectrumAvg_Pxy) ./ abs(spectrumAvg_Pxx);
subplot(311);
plot(f,20*log10(H2));
title("幅频曲线(自己实现的自功率谱、互功率谱估计)");xlabel("频率");ylabel("db");%% 自带pwelch、cpsd
[Pxx,f1] = pwelch(in, hanning(winlen),overlap,winlen,fs);
[Pxy,f2] = cpsd(in, out, hanning(winlen),overlap,winlen,fs);subplot(312);
plot(f1, 20*log10(abs(Pxy ./ Pxx)));
title("幅频曲线(自带的pwelch、cpsd函数)");xlabel("频率");ylabel("db");%% freqz理想幅频特性曲线
[H3, w] = freqz(b,a);
subplot(313);f1 = w*fs/2/pi;
plot(f1,20*log10(abs(H3)));
title("幅频曲线(理想)");xlabel("频率");ylabel("db");结果图:

遗留问题:
该示例中使用高阶滤波器后,幅频特性曲线仍会有较大的波动,有待在后续学习中解决。
相关文章:

使用自功率谱、互功率谱估计滤波器幅频特性
这段时间终于对工程中的随机信号的一般处理方式有点头绪了,功率谱密度估计是十分重要的方式之一,仍需继续深入细化相关内容。 示例:使用自功率谱、互功率谱估计滤波器幅频特性,自己实现 & Matlab自带函数实现。 clc;clear;cl…...

51单片机光照强度检测自动路灯开关仿真( proteus仿真+程序+报告+讲解视频)
51单片机光照强度检测自动路灯开关仿真( proteus仿真程序报告讲解视频) 仿真图proteus7.8及以上 程序编译器:keil 4/keil 5 编程语言:C语言 设计编号:S0052 讲解视频 基于51单片机的光照检测自动路灯控制仿真设计( proteus仿…...

socat管理haproxy配置
文章目录 前言一、配置二、简单使用1. 先安装 socat2. 获取 haproxy 的监控数据 总结 前言 我们可以通过 socat 命令 实现对 haproxy 的管理,包括获取监控数据,对后端服务器实现启动停止,服务流量控制等等。 一、配置 要想 haproxy 支持通过…...

Linux发行版X华为鲲鹏openEuler
前言 作为硬件和软件之间的桥梁,我接触的最多的就是Windows和Centos,还记得最初的鸟哥的Linux私房菜,而Centos即将停止维护更新(Centos7维护到2024),对于个人学习来说没有任何影响,但是对于企业…...
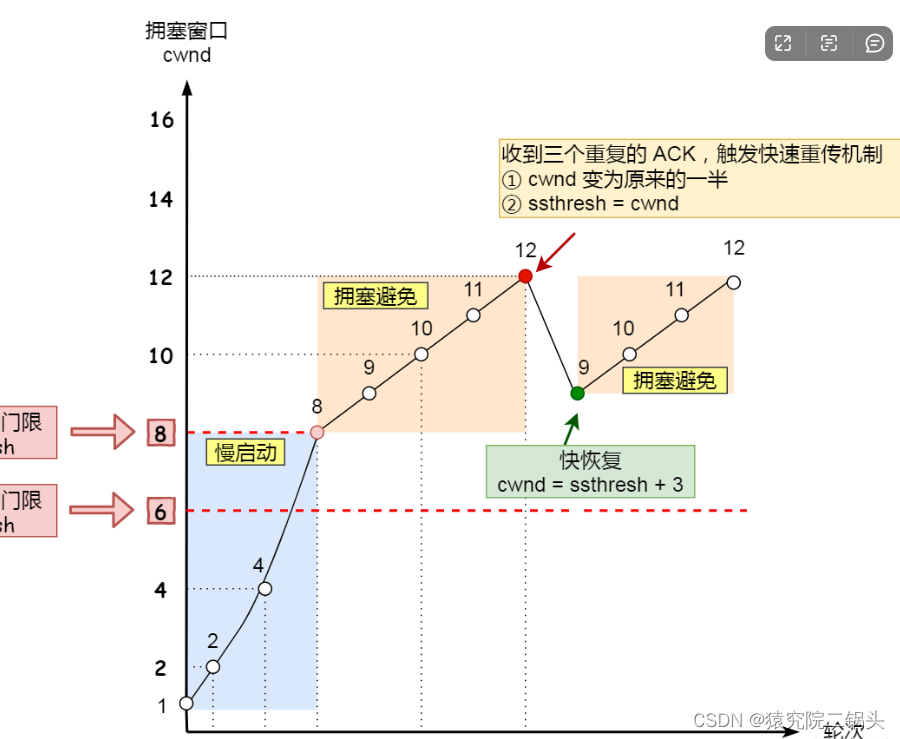
计算机网络相关知识点
谈一谈对OSI七层模型和TCP/IP四层模型的理解? 这两种模型都是网络通信中重要的参考模型,他们的设计和功能有一些区别。 首先OSI,OSI七层模型,也被称为开放系统互联参考模型,是一种在国际标准化组织(ISO)中…...
Jmeter+Ant+Git+Jenkins持续集成介绍
【软件测试面试突击班】如何逼自己一周刷完软件测试八股文教程,刷完面试就稳了,你也可以当高薪软件测试工程师(自动化测试) 一 简介 1.什么是ant? ant是构建工具 2.什么是构建 概念到处可查到,形象来说ÿ…...

Spring Cloud Gateway实战WebFlux解析请求体及抛出指定错误代码和信息
概述 基于Spring Cloud开发微服务时,使用Spring Cloud原生自带的Gateway作为网关,所有请求都需要经过网关服务转发。 为了防止恶意请求刷取数据,对于业务请求需要进行拦截,故而可在网关服务增加拦截过滤器。基于此,有…...
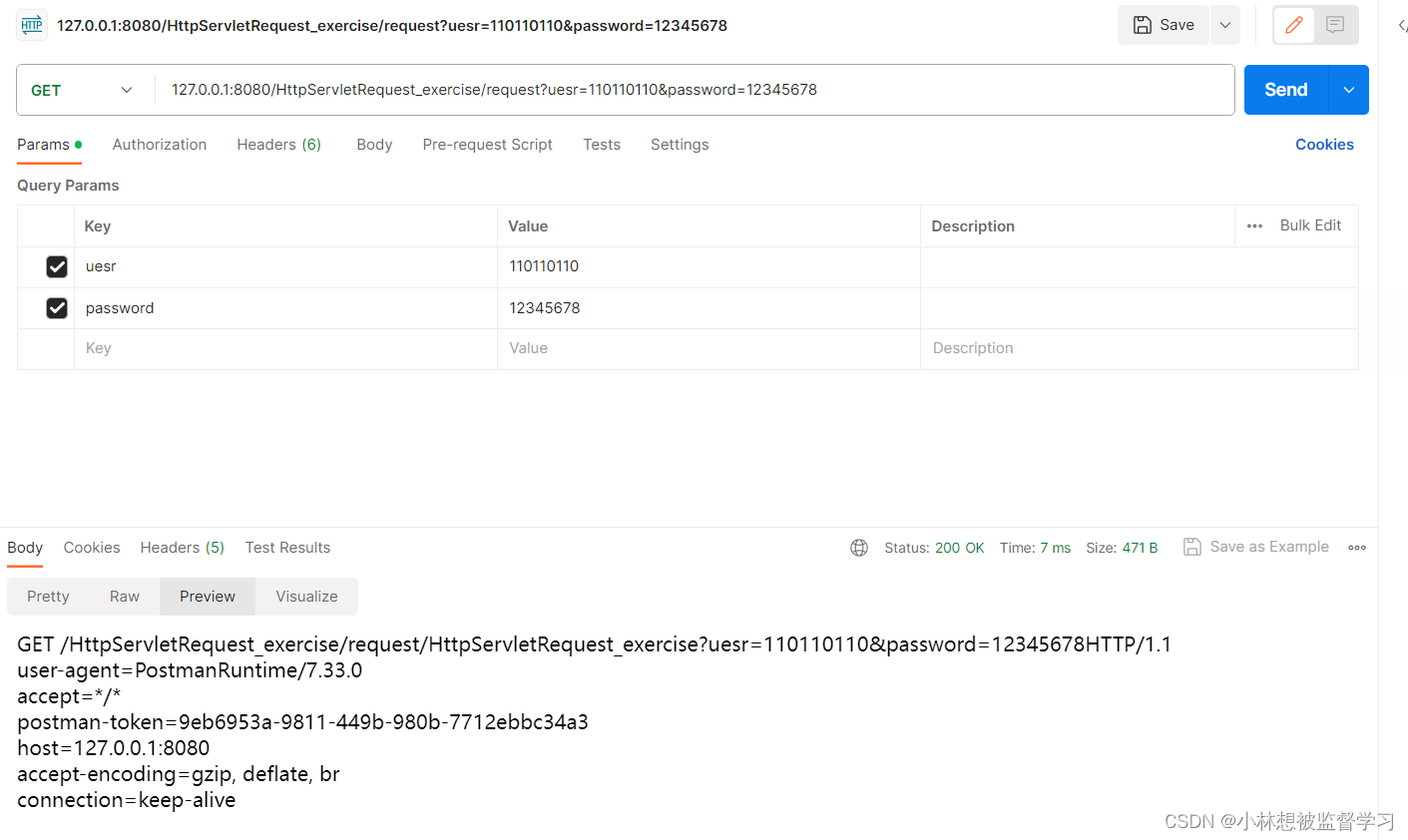
Servlet开发-通过代码案例熟悉HttpServletRequest类
关于Servlet开发的流程推荐看servlet开发-通过Tomcat部署一个简单的webapp Servlet开发与idea集成的插件安装推荐看idea集成tomcat(Smart Tomcate插件安装) postman(第三方创建HTTP请求工具)的安装推荐看创建HTTP请求的几种方式…...
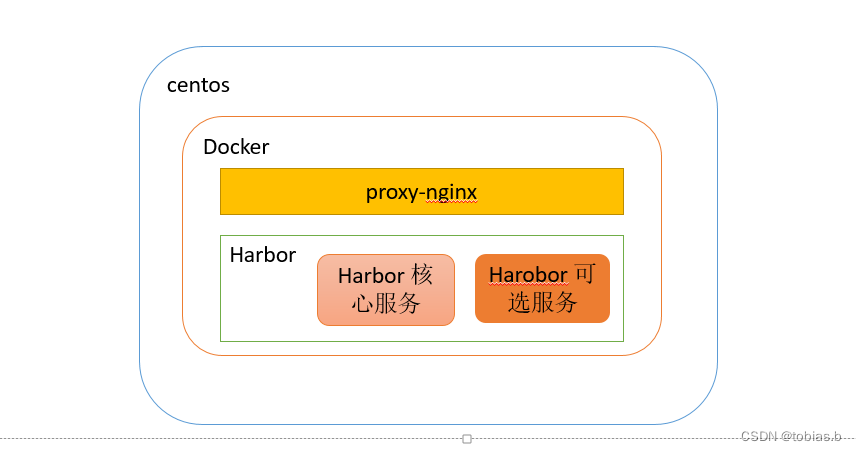
离线环境harbor 搭建及使用
一 摘要 本文主要介绍harbor 的安装及使用。 二 环境信息及部署图 2.1 环境信息 名称版本备注操作系统centos7.9容器docker 23.0.1harbor2.7代理nginx待补充 2.2 架构图 说明: 1.harbor 核心服务里有个nginx ,也可以用该nginx 做代理 2.proxy-ngin…...
华为杯数学建模比赛经验分享
再过一周左右,第二十届华为杯数学建模比赛就要开赛了,所以今天分享一下个人数学建模比赛的经验。 今天给大家分享一期关于华为杯数学建模比赛的经验分享,我将从以下三个方面展开说明: (1)如何准备数学建模比赛&#x…...

c语言 - 实现每隔1秒向文件中写入当前系统时间
实现思路 主要是通过库函数和结构体获取当前系统时间(年月日和时分秒)保存到变量里,然后通过格式化输出函数将当前系统时间输出到文件中去。 但是需要注意的是题目要求每隔 1 s对系统时间进行输出,所以需要加入 sleep()函数进行调…...
使用cpolar端口映射的方法轻松实现在Linux环境下SVN服务器的搭建与公网访问
文章目录 前言1. Ubuntu安装SVN服务2. 修改配置文件2.1 修改svnserve.conf文件2.2 修改passwd文件2.3 修改authz文件 3. 启动svn服务4. 内网穿透4.1 安装cpolar内网穿透4.2 创建隧道映射本地端口 5. 测试公网访问6. 配置固定公网TCP端口地址6.1 保留一个固定的公网TCP端口地址6…...
前后台分离开发 YAPI平台 前端工程化之Vue-cli
目录 YAPI介绍前端工程化之Vue-cli前端工程化简介前端工程化入门——Vue-cli环境准备Vue项目简介创建Vue项目vue项目目录结构介绍vue项目运行方法 Vue项目开发流程 前后台混合开发这种开发模式有如下缺点: 沟通成本高:后台人员发现前端有问题࿰…...

【js/es6】合集
目录 随机生成字符串每十个字符换行 随机生成字符串 function generateRandomAlphaNum(len) {var rdmString "";for (; rdmString.length < len; rdmString Math.random().toString(36).substr(2));return rdmString.substr(0, len); }每十个字符换行 string.…...

Nginx modules build fail:field ‘pkt6’ has incomplete type
前言 最近升级Nginx 1.24.0,编译第三方module出错: /usr/src/nginx_modules/ngx_json_post_module/src/ngx_json_post_module.c In file included from src/event/ngx_event.h:526,from src/http/ngx_http_upstream.h:14,from src/http/ngx_http.h:34,…...

电脑突然提示mfc140u.dll丢失,缺失mfc140u.dll无法运行程序的解决方法
在当今信息化社会,电脑已经成为我们生活和工作中不可或缺的一部分。然而,随着技术的不断发展,电脑也会出现各种问题。其中,最常见的问题之一就是“mfc140u.dll丢失”。那么,当我们遇到这个问题时,应该如何解…...

国庆day1
消息队列 代码 发送 #include<myhead.h> //声明一个消息结构体 typedef struct {long msgtype; //消息类型char data[1024]; //消息正文 }Msg_s; #define SIZE sizeof(Msg_s)-sizeof(long) //消息正文的大小 int main(int argc, const char *argv[]) {key_t key; /…...
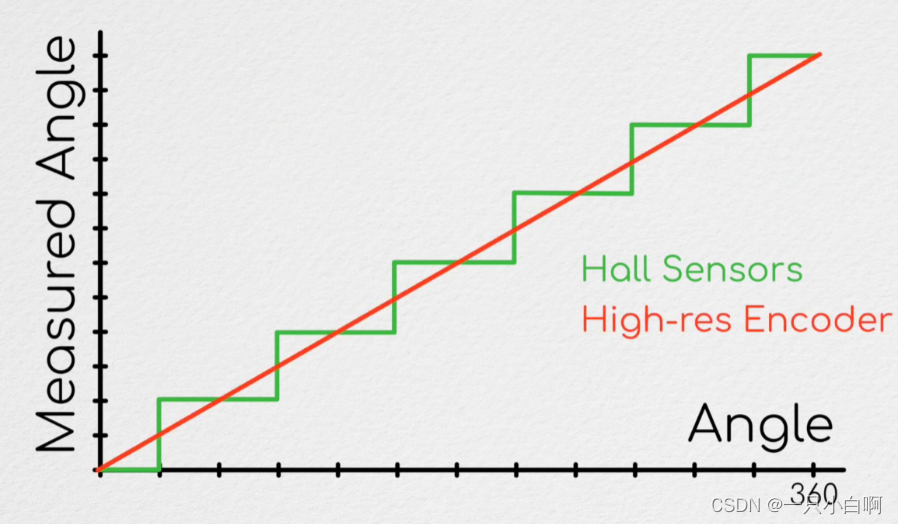
从零开始之了解电机及其控制(11)实现空间矢量调制
广泛地说,空间矢量调制只是将电压矢量以及磁场矢量在空间中调制到任意角度,通常同时最大限度地利用整个电压范围。 其他空间矢量调制模式确实存在,并且根据您最关心的内容,它们可能值得研究。 如何实际执行这种所谓的交替反向序列…...

如何将html转换成markdown
什么是Turndown “Turndown” 是一个用于将 HTML 转换为 Markdown 的 JavaScript 库。它通常用于将富文本内容从网页或其他 HTML 格式转换为纯文本 Markdown 格式,以便在不同平台上显示或存储。 如果在有node环境的情况下要使用 Turndown,首先需要将它…...

【VUE复习·3】@keyup.xxx 键盘事件触发函数(单按键 or 组合按键触发)
总览 1.keyup.xxx or keydown.xxx 单按键触发 2.组合按键触发 一、keyup.xxx or keydown.xxx 1.用法 在我们使用 keyup.enter 时,那么我们可以这样写: <div><input type"text" placeholder"按下回车键以确定..." keyu…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...
