医疗图像分割指标
医疗图像其中两种图像格式:MRI(Magnetic Resonance Imaging,磁共振成像)、CT(Computed Tomography,计算机断层),常存成 .nii.gz 格式。都是 3D 的 H × W × L H \times W \times L H×W×L,但不是 RGB,而是类似 grey-scale 图只有一个 channel,如 CT 的值可能是 Hu 值,取值范围可从负几千到正几千,参考 [1]。segmentation label 也相应是 3D 的。

这里记录几种分割指标,参考 [2,3],可调 medpy 的包,其文档也有指标列表。记有 C + 1 个类,0 固定是 background,(某个数据的)prediction 和 label Y ^ , Y ∈ { 0 , … , C } H × W × L \hat{Y},Y\in \{0, \dots, C\}^{H \times W \times L} Y^,Y∈{0,…,C}H×W×L,只留下第 c 类的 binary prediction 和 label 为 B ^ c , B c ∈ { 0 , 1 } H × W × L \hat{B}^c,B^c \in \{0, 1\}^{H \times W \times L} B^c,Bc∈{0,1}H×W×L, ∣ ⋅ ∣ |\cdot| ∣⋅∣ 表示非零元素个数, B ^ c , B c \hat{B}^c,B^c B^c,Bc 的 surface / boundray 记为 S ^ c , S c \hat{S}^c, S^c S^c,Sc,是其表面 voxels 的三维索引向量(下标)的集合。
Dice Coefficient
即 F1-scoure[2]。第 c 类的 dice 系数: D C c = 2 ∣ B ^ c ∩ B c ∣ ∣ B ^ c ∣ + ∣ B c ∣ DC_c=\frac{2|\hat{B}^c \cap B^c|}{|\hat{B}^c| + |B^c|} DCc=∣B^c∣+∣Bc∣2∣B^c∩Bc∣ 调包:medpy.metric.binary.dc。
IoU
即 Jaccard 系数[2]。第 c 类的 IoU: I o U c = ∣ B ^ c ∩ B c ∣ ∣ B ^ c ∪ B c ∣ IoU_c = \frac{|\hat{B}^c \cap B^c|}{|\hat{B}^c \cup B^c|} IoUc=∣B^c∪Bc∣∣B^c∩Bc∣ 调包:medpy.metric.binary.jc。由 [3],IoU 与 dice 系数有确定的转换关系,即等价,所以两者应该用其中一种就行。C 类的 IoU 取平均就是 mIoU: m I o U = ∑ c = 1 C I o U c C mIoU=\frac{\sum_{c=1}^{C}IoU_c}{C} mIoU=C∑c=1CIoUc(2023.9.28:不确定算 mIOU 时要不要加上 background)
Sensitivity
即 recall,也叫 TPR(True Positive Rate),非对称。第 c 类的 sensitivity: R c = ∣ B ^ c ∩ B c ∣ ∣ B c ∣ R_c=\frac{|\hat{B}^c \cap B^c|}{|B^c|} Rc=∣Bc∣∣B^c∩Bc∣ 调包:medpy.metric.binary.sensitivity 或 medpy.metric.binary.recall。
Specificity
也叫 selectivity、TNR(True Negative Rate),是 sensitivity 的补。第 c 类的 specifity: S P c = ∣ ( 1 − B ^ c ) ∩ ( 1 − B c ) ∣ ∣ ( 1 − B c ) ∣ SP_c = \frac{|(1-\hat{B}^c) \cap (1-B^c)|}{|(1-B^c)|} SPc=∣(1−Bc)∣∣(1−B^c)∩(1−Bc)∣ 调包:medpy.metric.binary.specificity。
Average (Symmetric) Surface Distance
由 [4],第 c 类的 average surface distance: A S D ( S ^ c , S c ) = ∑ p ∈ S ^ p c d s ( p , S c ) / ∣ S ^ c ∣ ASD(\hat{S}^c, S^c) = \sum_{p \in \hat{S}^c_p} d_s(p,S^c) \big/ |\hat{S}^c| ASD(S^c,Sc)=p∈S^pc∑ds(p,Sc)/∣S^c∣ 其中 d s ( ⋅ , ⋅ ) d_s(\cdot,\cdot) ds(⋅,⋅) 是点到点集(此处是表面 S)距离: d s ( p , S ) = min q ∈ S d ( p , q ) d_s(p,S)=\min_{q \in S} d(p,q) ds(p,S)=q∈Smind(p,q) p , q ∈ { 1 , … , W } × { 1 , … , H } × { 1 , … , L } p,q \in \{1,\dots,W\} \times \{1,\dots,H\} \times \{1,\dots,L\} p,q∈{1,…,W}×{1,…,H}×{1,…,L} 是三维索引向量(下标), d ( ⋅ , ⋅ ) d(\cdot,\cdot) d(⋅,⋅) 是欧氏距离。就是对 S ^ \hat{S} S^ 中属于此 object 表面的每一个 voxel,都算一下它到 S 的距离,然后取平均。调包:medpy.metric.binary.asd。
ASD 不对称,一般会用 ASSD: A S S D ( S ^ c , S c ) = A S D ( S ^ c , S c ) + A S D ( S c , S ^ c ) 2 ASSD(\hat{S}^c, S^c) = \frac{ASD(\hat{S}^c, S^c) + ASD(S^c, \hat{S}^c)}{2} ASSD(S^c,Sc)=2ASD(S^c,Sc)+ASD(Sc,S^c) 调包:medpy.metric.binary.assd。有些文章也会将 ASSD 简叫成 ASD,感觉可以无脑只用 ASSD。
Hausdorff Distance
由 [2,4],第 c 类的 Hausdorff 距离: H D ( S ^ c , S c ) = max { sup p ∈ S ^ c d s ( p , S c ) , sup p ∈ S c d s ( p , S ^ c ) } HD(\hat{S}^c,S^c)=\max\left\{ \sup_{p \in \hat{S}^c} d_s(p, S^c), \sup_{p \in S^c} d_s(p, \hat{S}^c) \right\} HD(S^c,Sc)=max{p∈S^csupds(p,Sc),p∈Scsupds(p,S^c)} 调包:medpy.metric.binary.hd。
Code
- 分割模型应该一般 predict 的都是 (C+1)-way softmax prediction,即 Y ^ \hat{Y} Y^。
from collections import defaultdict
import numpy as np
from medpy.metric.binary import dc, jc, hd, assd, sensitivity, specificitydef evaluate(Y_pred, Y_true, n_classes):""""medical segmentation evaluationInput:Y_pred, Y_true: [H, W, L], in {0, ..., n_classes - 1}n_classes: intOutput:res: {<metric_name>: [<class_0>, ..., class_nc-1]}"""metric_names = ("dice", "sensitivity", "specificity", "assd", "hd")#, "iou")metric_fn = (dc, sensitivity, specificity, assd, hd)#, jc)res = defaultdict(list)for c in range(n_classes):B_pred_c = (Y_pred == c).astype(np.uint8)B_c = (Y_true == c).astype(np.uint8)for metr, fn in zip(metric_names, metric_fn):res[metr].append(fn(B_pred_c, B_c))return res
References
- 亨氏单位
- 常用的医学图像分割评价指标
- 医学图像分割常用指标及代码(pytorch)
- (MIA 2022) Rethinking adversarial domain adaptation: Orthogonal decomposition for unsupervised domain adaptation in medical image segmentation - paper, github
相关文章:

医疗图像分割指标
医疗图像其中两种图像格式:MRI(Magnetic Resonance Imaging,磁共振成像)、CT(Computed Tomography,计算机断层),常存成 .nii.gz 格式。都是 3D 的 H W L H \times W \times L HWL…...
零代码编程:用ChatGPT批量修改文件夹名称中的大小写
一个文件夹下面有很多个子文件夹,要把文件夹中的大写数字全部重命名为小写数字,比如将二 三 四,改成: 2 34 在ChatGPT中输入提示词如下: 你是一个Python编程专家,要完成一个文件夹重命名的任务。具体步骤如…...

webpack:详解cache模块常用配置
背景 持久化缓存算得上是 Webpack 5 最令人振奋的特性之一,它能够将首次构建结果持久化到本地文件系统,在下次执行构建时跳过一系列解析、链接、编译等非常消耗性能的操作,直接复用 module、chunk 的构建结果。 cache 会在开发模式被设置成…...

云原生Kubernetes:Pod控制器
目录 一、理论 1.Pod控制器 2.Deployment 控制器 3.SatefulSet 控制器 4.DaemonSet 控制器 5.Job 控制器 6.CronJob 控制器 二、实验 1.Deployment 控制器 2.SatefulSet 控制器 3.DaemonSet 控制器 4.Job 控制器 5.CronJob 控制器 三、问题 1. showmount -e 报错…...

数据库基础与MySQL入门
在当今的数字化世界中,数据如同生命之水,它贯穿于各种应用和服务中。尤其在游戏行业,例如经典的《三国志》,数据库管理成了一个不可或缺的环节。这不仅涉及到用户信息的存储,还涉及到游戏状态、积分、交易等复杂的数据处理需求。 MySQL作为一个广受欢迎的数据库管理系统,…...

探索Java爬虫框架:解锁网络数据之门
引言: 随着互联网时代的发展,大量的数据被存储在各种网页中。对于开发者而言,如何高效地获取和处理这些网络数据成为了一个重要的问题。而Java作为一门强大的编程语言,也有许多优秀的爬虫框架供开发者选择和使用。本文将带您深入…...

智慧燃气平台的总体架构到底应怎样设计?
关键词:智慧燃气、智慧燃气平台、智能燃气、智能监控 智慧燃气平台功能设计的一些方向和思考: 1、资源统一,管理调度 城市燃气智慧调度运营管理平台收集并且整理出每个业务系统信息,并且根据所整理出的信息结果制定出标准规范&…...
MonkeyRunner测试步骤
首先把安卓SDK的 环境变量给配置好,这里就不再多解释,自己google 然后将自己的安卓设备打开调试模式,USB连接至电脑,运行CMD,输入命令adb devices 查看你的安卓设备的ID(ID后面写程序会调用),…...

Konva基本处理流程和相关架构设计
前言 canvas是使用JavaScript基于上下文对象进行2D图形的绘制的HTML元素,通常用于动画、游戏画面、数据可视化、图片编辑以及实时视频处理等方面。基于Canvas之上,诞生了例如 PIXI、ZRender、Fabric、Konva等 Canvas渲染引擎,兼顾易用的同时…...

人工智能AI知多少?
摘要 人工智能(Artificial Intelligence,简称AI)是一项前沿技术,正在快速发展并渗透到各个领域。然而,对于大多数人来说,人工智能仍然是一个陌生而复杂的概念。本文旨在对人工智能进行扫盲,介绍其基本概念、应用领域以及当前热门的人工智能模型。通过具体的例子,读者将…...

leetcode1610. 可见点的最大数目(java)
可见点的最大数目 题目描述滑动窗口 题目描述 难度 - 困难 leetcode1610. 可见点的最大数目 给你一个点数组 points 和一个表示角度的整数 angle ,你的位置是 location ,其中 location [posx, posy] 且 points[i] [xi, yi] 都表示 X-Y 平面上的整数坐标…...
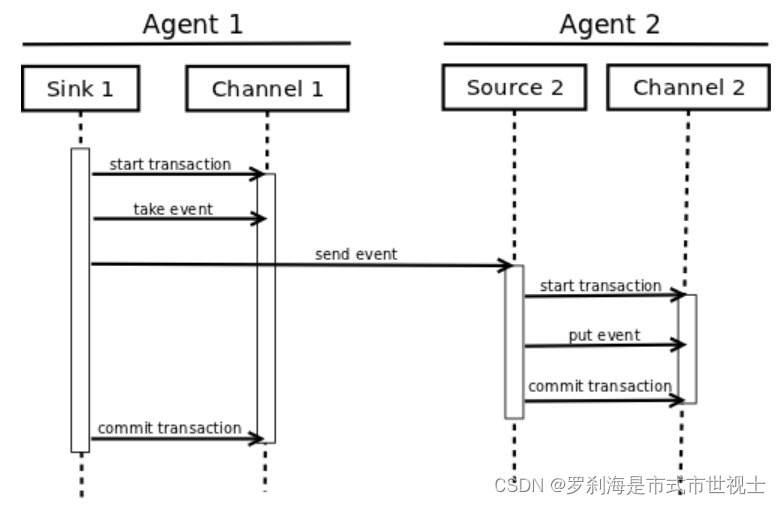
Apache Flume
Flume 1.9.0 Developer Guide【Flume 1.9.0开发人员指南】 Introduction【介绍】 摘自:Flume 1.9.0 Developer Guide — Apache Flume Overview【概述】 Apache Flume is a distributed, reliable, and available system for efficiently collecting, aggregati…...

【切片】基础不扎实引发的问题
本次文章主要是来聊聊关于切片传值需要注意的问题,如果不小心,则很容易引发线上问题,如果不够理解,可能会出现奇奇怪怪的现象 问题情况: 小 A 负责一个模块功能的实现,在调试代码的时候可能不仔细&#x…...

CVE-2023-5129 libwebp堆缓冲区溢出漏洞影响分析
漏洞简述 近日苹果、谷歌、Mozilla和微软等公司积极修复了libwebp组件中的缓冲区溢出漏洞,相关时间线如下: 9月7日,苹果发布紧急更新,修复了此前由多伦多大学公民实验室报告的iMessage 0-click 漏洞,漏洞被认为已经被…...

leetcode做题笔记155. 最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。 实现 MinStack 类: MinStack() 初始化堆栈对象。void push(int val) 将元素val推入堆栈。void pop() 删除堆栈顶部的元素。int top() 获取堆栈顶部的元素。int get…...

蓝海彤翔亮相2023新疆网络文化节重点项目“新疆动漫节”
9月22日上午,2023新疆网络文化节重点项目“新疆动漫节”(以下简称“2023新疆动漫节”)在克拉玛依科学技术馆隆重开幕,蓝海彤翔作为国内知名的文化科技产业集团应邀参与此次活动,并在美好新疆e起向未来动漫展映区设置展…...

【AI视野·今日NLP 自然语言处理论文速览 第四十四期】Fri, 29 Sep 2023
AI视野今日CS.NLP 自然语言处理论文速览 Fri, 29 Sep 2023 Totally 45 papers 👉上期速览✈更多精彩请移步主页 Daily Computation and Language Papers MindShift: Leveraging Large Language Models for Mental-States-Based Problematic Smartphone Use Interve…...
【VsCode】vscode创建文件夹有小图标显示和配置
效果 步骤 刚安装软件后, 开始工作目录下是没有小图标显示的。 如下图操作,安装vscode-icons 插件,重新加载即可 创建文件夹,显示图标如下:...

celery分布式异步任务队列-4.4.7
文章目录 celery介绍兼容性简单使用安装使用方式 功能介绍常用案例获取任务的返回值任务中使用logging定义任务基类 任务回调函数No result will be storedResult will be stored任务的追踪、失败重试 python setup.py installln -s /run/shm /dev/shmOptional configuration, …...

解决M2苹果芯片Mac无法安装python=3.7的虚拟环境
问题描述 conda无法安装python3.7的虚拟环境: conda create -n py37 python3.7出现错误 (base) ➜ AzurLaneAutoScript git:(master) conda create -n alas python3.7.6 -y Collecting package metadata (current_repodata.json): done Solving environment: fa…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
